The question for today is how does realclimate go from tree ring series with autocorrelation functions that look like the one in the figure below to a claim that these proxies have an AR1 coefficient of 0.15. We know that they are pranksters, but this looks like a good prank and it is.

Autocorrelation Function for Sheep Mountain. AR1 coefficient is 0.7. Red line shows rapid exponential decay of even an AR1=0.7 autocorrelation.
One of our readers (and their readers) wrote to them and wondered whether they had taken first differences prior to doing their calculations. (This turns out to be the case, or at least part of the story, as shown below.) Mann categorically denied that any first differencing took place.
The article you link to uses a differencing technique “to remove the large variance highly correlated slow component from consideration prior to determining the AR1 autocorrelation component.”
This doesn’t sound like a straight-forward estimate of an autocorrelation coefficient. What do you get if you use the standard method of estimating autocorrelation coefficients? Also, in the Von Storch analysis, which type of model are they using: a standard AR1 model, or a model that corresponds to this differencing technique that removes the highly correlated slow component?
Thanks in advance for the clarification.
[Response: You misunderstand what he’s done. He hasn’t performed any differencing of the data at all. He has simply calculated the lag-1 autocorrelation coefficient of the actual proxy data and has provided an argument for why this should be representative of the noise autocorrelation. In fact, it is easy to verify that this is the case using synthetic examples from climate model simulations with added AR(1) noise. -mike]
The reader wrote back and again Mann denied any first differencing.
If you could indulge me some more, I need some more education.
My reading of the Ritson paper you link to suggests that the differencing technique he uses removes ANY highly autocorrelated slow component before calculating the AR1 coefficient.
My question then is, what happens if there is NO temperature signal in the data, but there IS an extraneous, highly autocorrelated signal that is not temperature related (say a CO2 fertilization effect or a precipitation signal). Does the procedure remove the confounding, signal? Presumably the procedure cannot tell the difference between the “true” signal and an extraneous signal with the same statistical properties. So is it possible the procedure is removing exactly the type of red noise that Von Storch is trying to simulate?
[Response: You misunderstand what he’s done. He hasn’t performed any differencing of the data at all. He has simply calculated the lag-1 autocorrelation coefficient of the actual proxy data and has provided an argument for why this should be representative of the noise autocorrelation. In fact, it is easy to verify that this is the case using synthetic examples from climate model simulations with added AR(1) noise. -mike]
Now let’s look at Ritson’s description of what he did, as shown in the following excerpts. His autocorrelation coefficients [àŽ⯠] are calculated from the series Y, which are clearly the first differences of the original proxy series X. So Mann is pulling our legs when he says that there is no first differences (sort of like him saying, I did not have r2 with that statistic, Miss Lewinsky).

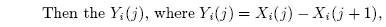
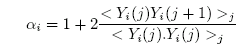
If one calculates results according to his last formula on the 70-series AD1400 MBH98 tree ring network, conveniently archived at GRL in connection with our paper last year, sure enough one gets an average of 0.14 for the period 1400-1980. I got a little bit higher value for the period 1400-1880, said by Ritson to have been used in his calculations. I’m not sure what the differences are, but it looks like I’ve replicated his calculations.
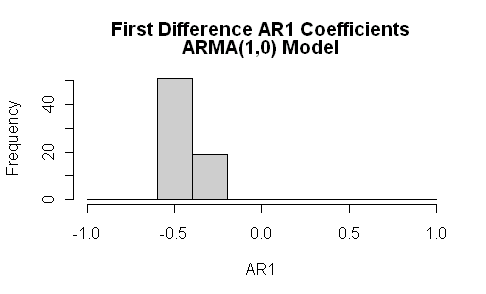
The formula shown by Ritson would hold for an AR1 process. Simple prudence would dictate that one calculate the actual AR1 coefficient. The software is convenient and it takes one line of code to do and another line to graph. In fact, the actual AR1 coefficients, calculated freshly are strongly negative.
When one is looking at ARMA models, it’s always a good idea to look at more than AR1 models and, for climate series, I think that it should be mandatory to look at ARMA(1,1) models. Again the differences are striking. Instead of the AR1 coefficients being negative, they are more widely dispersed and there is a very, very strong MA1 coefficient.
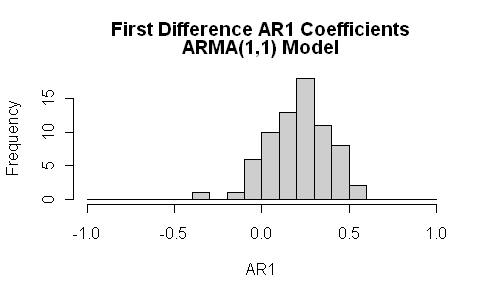
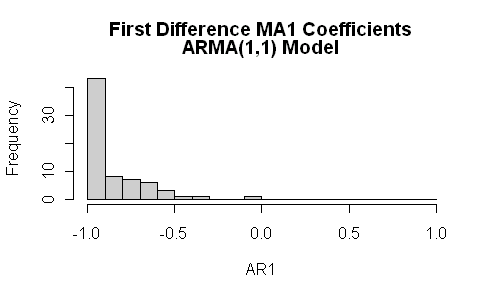
I looked specifically at confidence intervals for Sheep Mountain (illustrated above) and, for the first differences used by Ritson, the AR1 coefficient was 0.08 (se 0.06) and MA1 coefficient -0.75 (se 0.04). This was a series with an AR1 coefficient near 1 modeled on the proxy data itself.
Now think about what would happen under the Ritson method if you are started with a random walk. First differencing transforms the Y series to white noise, which would have Ritson coefficient of 0. This is a total fiasco. It makes Rasmus look competent.




108 Comments
The Ritson calculation is not published I see, and is just a pdf somewhere. So the post as a whole seems like a ‘trial balloon’ precursing another rebuttal. In one way it is a good example of a worthwhile use of blogs — to get feedback outside the converted ones. Plenty of cheering from the usual suspects at RC too. In an adversarial sense its a pity they didn’t keep it under wraps until publication.
Who says maths isn’t fun …
Re #1: The blogs actually do serve a useful purpose in cases like this. Ritson will have received a lot of free and excellent advice — he might have preferred somewhat less publicity — and presumably he will now be able to fix the errors and move forward. That’s all to the good.
I am not sure what to make of Mann’s denial that Ritson did what Ritson himself says he did (at least I can’t come up with a different interpretation of the blogs and Ritson’s pdf).
You must be referring to the following-
RC#11: “The article you link to uses a differencing technique”
Mann: “You misunderstand what he’s done. He hasn’t performed any differencing of the data at all…”
RC#12: “My reading of the Ritson paper you link to suggests that the differencing technique he uses…”
Mann: “You misunderstand what he’s done. He hasn’t performed any differencing of the data at all…”
RC#20: “#11 & #12, I guess I am confused like Terry. In Ritson’s paper, the third equation down, it appears that the proxy data is differenced Y(j)=X(j)-X(j-1) ??? Phil”
Mann: “We’re checking with David Ritson for confirmation…”
I guess 3rd time’s a charm!
Classic the way he just copied and pasted his reply to the first comment like he was talking to a child. Well done Terry and Phil B.
It’s bizarre how he still hasn’t really admitted that first differences were used and has some opaque update that could be read either way and has non-sequiters in it.
I wonder if there is any rowback being inserted into the top post without a correction being shown. For example, the parenthetical “even 0.3” comment.
I’m not accusing, by the way. Just want to watch out for that sort of thing.
I sent the following post earlier today to realclimate. Needless to say, they censored it.
#7. I think that you’re right about the 0.3. Notice that Mann has switched from talking about the 70-series AD1400 tree ring network that Ritson used to talking about the 112-series network.A couple of points.
You’d think that Mann would know enough about his wretched tree ring network to know that Ritson had goofed in his AR1 calculations.
Second, you’d think that they’d just fess up their error and get on with it. It seems to be physiologically impossible for Mann to admit an error.
Third, “average” redness is an absolutely ludicrous concept. If you look back at this post http://www.climateaudit.org/?p=370 which is well worth re-reading, as long as you’ve got one HS shaped series in a white noise network, the MAnnian regression method mines for it (this is over and above the PC mining). So I got reconstructions just as good as MBH using dot.com stocks and white noise.
That post is really very good in illustrating what is actually goin on in MBH98. Especially when you see all their blithering about white or slightly red noise. What you have is one HS shaped series whose values run REALLY cold throughout its history. The residuals from the bristlecones would indicate that California was in an Ice Age throughout the millennium; while all the other proxies differ little from noise.
Watching the pea under the thimble, Mann is trying to shift focus to the 112 proxy network and away from the flaqwed early netwrok.
It’s amazing to
Too much …..
“#22 Mike, Thanks for your quick response and patience. Phil
[Response: We’re happy to answer good faith questions such as yours here. Others, however, who seem to pose questions that gratuitously ignore answers already provided previously, are unlikely to see their comments get screened through. -mike]
Comment by Phil B. “¢’¬? 25 May 2006 @ 7:18 pm”
After denying that Ritson had done first differencing, Mann could not bring himself to admit that Ritson had done first differencing. Mann said:
In the context of two previous statements by Mann that Ritson had not done first differencing, what does that mean? I guess it means that he realizes that he was wrong, but there’s no way that he’s going to admit it. Also he doesn’t deal with the stupidity of Ritson’s method. The “Ritson-autocorrelation” of a random walk is 0, as compared to a true value of 1.
But of course, as with any Mann error, it “doesn’t matter”. Unless of course you touch the bristlecone series. THen hell hath no fury like realclimate.
as far as I can understand, Ritson is estimating the autocorrelation of the “noise”, instead of the autocorrelation of the series; is that right ? Can it really be that Mike is truly saying that “the assumption of low signal-to-noise ratios” is true for these series ? (#22)
Is Ritson making the precise point that VS introduced autocorrelated noise, whereas the real data series do not show short term autocorrelated noise ? The real data series presumably show longer term autocorrelation ?
sorry for my poor statistics !
per
I’m beginning to wonder if the RC thread might be an elaborate hoax, some kind of post-modern internet-based performance art. I cannot come up with a better explanation. Surely Mann knows the technical issues here — this material is covered in intro time-series classes — so can someone please let me in on what this is really about?
I think performance art is the mot juste. Where is Rasmus when we need him – http://www.climateaudit.org/?p=464.
I remain baffled by this whole thing. In my RealClimate posts, I quote Ritson’s rather plain language a number of times, so I don’t understand how I could have been so far off in my interpretation.
Oh, and my point about how Ritson’s technique (based on the text of his first paragraph) would probably remove any high correlation noise component from the data and thereby throw out exactly the high-correlation noise we are looking for, was never responded to.
Steve wrote:
This might be the key to the whole thing. Ritson (in his first paragraph) writes that he removes “the large variance highly correlated slow component from consideration prior to determining the AR1 autocorrelation component.” Well, if you remove the high-correlation component before doing your calculation, aren’t you, by construction, going to ge a low correlation estimate?
Steve seems to show that the resulting estimate is, by construction, zero. If so, the puzzle is how Ritson is able to get an estimate as high as 0.15 plus or minus 0.06. Why doesn’t he get an estimate of zero? (Or why isn’t zero at least within his confidence interval?)
Hmmm.
Terry, I think the answer is, the coefficient of 0 only applies to a truly random walk. This input data is not actually a random walk. It may have many properties of such but there is more going on there. Thus the differencing does not remove ALL the autocorrelation – only that which is part of the “first derivative”.
Sorry, I’m not a statistician so I am probably using all the wrong terms. But hopefully you understand what I’m saying. There are other ways to get autocorrelated data than a random walk, and ONLY in the case of a random walk will this method give you exactly 0. Anything differening from one will give a non-zero result. But you MAY be able to show that in most (all?) circumstances the results will be lower in magnitude than those coming out of a standard autocorrelation test.
Question: Am I correct in thinking the only set of data which has an autocorrelation coefficient of 0 is white noise, or are there other functions which have that property?
If that’s true, then Ritson’s method will only give 0 for a random walk, because a random walk is the only function which, when differenced in that manner, gives white noise – I think. That’s assuming that any time you take a running total of white noise you get a random walk, which I think is true. So, if running total of white noise is a random walk, then the only function that will give you white noise when differenced in that manner is a random walk, and if the only function which has an autocorrelation coefficient of 0 is white noise, then what I have said above must be true.
I suspect there may be other functions which are not white noise but have autocorrelation of 0, but I’m not sure. I realize not all data is autocorrelated, but I suspect even data which you would not normally consider autocorrelated does not have a coefficient of 0, but merely a small one. Perhaps one of the resident statisticians knows an answer to this.
Thanks!
Re #18: Without getting too precise about what we mean, the short answer to your question is no: a lag-one autocorrelation of 0 does not generally imply “white noise”. If one restricts the stochastic process to be AR(1), or possibly AR(p), with some additional constraints the answer would be yes.
However, your question — and the whole silly RC debacle regarding Ritson/Mann and computing the ACF correctly — touches on an important topic that Steve has written about in the past: There exist rich classes of stationary stochastic processes that provide amazingly realistic models of natural variability and exhibit lag-one autocorrelations at or near 0.
My advice would be to set some time aside — this material is not easy — and take a serious look at the papers by Demetris Koutsoyiannis ( http://www.climateaudit.org/?p=483 ).
TAC: Thanks! That makes sense. It sounds to me based on what you said that AR(1) and AR(p) are rather simplistic functions for checking auto-correlation. I suppose the reason Steve is suggesting the use of ARMA as well is that it is a bit more sophisticated/complicated and might find auto-correlation where AR(1) would not.
Thank you, I would like to learn more about this—and statistics in general—I will read up on it when I have time.
TAC, thanks for the nice (i.e accurate and simple) explanation and for your mention to my papers. By the way, the easiest (I think) of my papers on this topic has been published just today (Nonstationarity versus scaling in hydrology, Journal of Hydrology,
http://dx.doi.org/10.1016/j.jhydrol.2005.09.022
and preprint avaliable in
http://www.itia.ntua.gr/e/docinfo/673/)
Nicholas and Terry and others, I firmly endorse TAC’s recommendation to spend time reading Demetris’ papers. Seemingly simple operations like standardizing a series by subtracting its mean and dividing by its standard deviation have quite different properties when applied to series that are not i.i.d.
It is irresponsible for a paleoclimatologist to EVER talk about i.i.d. distributions, as we have seen recently from Mann and Jones, as Rasmus done there. It gives a sense of false knowledge. As Satchell Paige said and this is probably the motto of this site, "the problem ain’t the things you don’t know; it’s the things you do know that ain’t so".
One of the main topics of climate is "high-frequency" and "low-frequency". Demetris has a very elegant stochastic model in which he allows for uncertainty on multiple scales – something that intuitively seems highly appropriate for climate – and is a far more "natural" stochastic model than fractional differencing – although fractional differencing will produce long-term persistence of the type shown in the autocorrelation function above.
I spent quite a bit of time pondering the autocorrelation properties of the above graphic as well as the autocorrelation properties of the Mannian North American PC1 which is even more autocorrelated. Mann’s reconstruction has "essential" proxies which CAN’T be "thrown out" and "non-essential" proxies, where errors "don’t matter".
The one that "matters" – the North American PC1/bristlecones – has HUGE autocorrelation. So the "average" autocorrelation doesn’t matter a good goddamn. 99% of the proxies can be white. He needs ONE proxy with huge autocorrelation and he gets it from the bristlecones. That’s why they imprint the reconstruction.
BTW in our GRL paper, we modeled the North American tree ring series by using fractional processes and I think that was one of the reasons why our models produced such "realistic" reproductions of Mann’s PC1. (Then all you need to do is make a proxy network with all the other series being white noise and you get a realistic looking "MBH98 reconstruction", not just a PC1, and many of them out-perform Mann’s. Thus no statistical significance. This is what is at the heart of our Reply to Huybers, although it occurs in a discussion of RE significance and has not been well understood. In part, it’s because my understanding of what was going on improved as I wrote up an account of our Reply to Huybers for the blog and the material on the blog is more advanced than the material that was published.
However, I think that Demetris’ concept of stochastic processes on multiple scales is a more elegant concept than fractional differences and I hope to improve my own understanding of the properties of this stochastic model in the future.
#18
Nicholas makes an important point – White noise is essentially unfiltered “noise”, (whatever that could mean). It is intrinsically random.
The instant one filters it to produce “red noise” or whatever, it ceases to be random and I suspect any statistics derived from these filtered models would be problematical philosophically, not the least theoretically.
Being orderly here 🙂
All the world is divided into two classes of people; those who don’t know which way interest rates are going and those who don’t know that they don’t know which way interest rates are going. I don’t even know who first said that, but I know it is true.
========================================
In my opinion Ritson has made two mistakes:
one, when he asserts that SZGJT based our last response to Wahl et in Science on the issue of red-noise pseudo-proxies. Although it is by now very reasonable to assume that tree-ring data
contain red-noise, our response shows clearly that MBH98 has problems even with white-noise pseudoproxies. I wonder if Ritson has look at the figure in our responser to Wahl et al.. Mann et al have also a simulation of the past millennium with the CSM. They just could show their results of their pseudo-reconstructions with their model, with white and red noise and detrended and non-detrended calibration. This could clarify this controversy.
The second one, as some of you have explained already, is that he used first differences of the original time series, thus actually pre-whitening the series. No wonder that the 1-lag autocorrelation is small. In my opinion, the question of the amount and structure of red-noise in the proxies is much more complicated that Ritson has pretended to show, even if his estimation of the 1-lag autocorrelation of the proxies had been correct. What has to be estimated is the autocorrelation of the noise, i.e. the part of the proxies independent of the climate signal. If the climate signal itself is red, I do not see an easy way of estimating the structure and magnitude of the noise at decadal timescales in a record that is just 100 years long. Perhaps econometrics may have a solution for this? co-integration or something in this direction?
eduardo
#22
Steve,
That operation in your first sentence is correct if, and only if, the measurements are normally distributed. I don’t know of any geoscientific data that are normally distributed, since all the ones I have experience with are lognormally, (or forbid something more incomprehensible) distributed.
Without getting into too much technical stuff, conventional stats also assume a standard “sample”, ie a human, or cannon ball, or widget. Statistically minded N=integers. (Humans are integers, cannon balls are integers, and we don’t deal with half humans since there is not integer of 0.5).
In geoscience these simple categories don’t exist naturally.
A tree is a tree and as an individual you could measure its mass.
As for its tree ring measurement, what would be the unit of measurement for the rings? When you measure tree rings you most certainly are measuring physical things, but things of what?
In mining and exploration this is defined as the sample support. Usually it is a constant volume but which raises how that volume is determined.
A tree could be cored by
1. 1 inch borer
2. 4 inch borer.
Measurements.
1. Tree rings appear linear and one measurement is made, and estimate is measurement.
2. Tree rings appear non linear and many measurements are made.
a- are measurements normal? yes – take mean as representative
b- are measurements not normal, try transformation to log normal. If THAT produces a normal distribution, then the logarithms of the tree-ring widths are used for the basis of statistical analysis.
Moral.
When exploration geologists start questioning basic statistical techniques, become extremely uncertain and sell all your stock.
#25. Eduardo, I think that there is a very direct way of doing what you are wondering about. It’s so obvious that you’ll wonder why people haven’t done this before, but no one has. I’ll post this up in a day or two as I have a little tidying to do first.
Eduardo,
I suppose context is everything, but autocorrelated noise/residuals are not of themselves a problem – econometricians deal with that sort of thing every day. We can use robust estimators where you don’t actually have to specify the precise form of autocorrelation but can use an upper bound (for example, Newey-West errors). You can also jointly estimate AR parameters for the noise and the signal. But you need to have a well specified underlying model.
Financial markets are blessed with a surfeit of data, and they routinely estimate very complicated models with ARCH (autoregressive conditional heteroskedasticity) errors and ‘core’ processes that are similar to random walks (stock prices or, rather, stock fundamentals). But even in macroeconomics where there is typically much less data (less even than in climate studies) you can estimate these sorts of models.
So, there should be hope – it’s just that you need to be careful, and the blithe assumptions that seem to be made by a lot of dendroclimatologists are anything but careful. (They seem worse than economists who assume the proverbial can opener[fifth paragraph at the link] – they seem to assume the fully cooked meal.)
Steve: It’s ironic that you tell this joke as I used exactly the same joke in our blog account of our Reply to Von Stroch and Zorita, arguing that their use of white noise amounted to assuming a can-opener as well. It’s curious to see that this is now the very topic that’s at argument – except the context is different. Ritson and Mann are arguing that their model was “too” red. We argued that their model was not nearly “red” enough. In this case, I firmly predict that the final answer is not going to be a Three Bears compromise, since the actual residuals of MBH proxies relative to the MBH reconstruction can be calculated and interpreted.
#25. I agree 100% that the Wahl, Ritson argument against your paper was irrelevant. White noise is orthogonal to any signal. The pseudoproxies as you constructed them consisted of signal plus white noise, so the attenuation that you observed is simply a form of the Pythagorean Theorem, when you think about it in those terms.
If you have low AR1 red noise, then again thinking of a vector sum, you have the equivalent of something that’s close to being a right-angled triangle and you can still talk about attenuation as you know that side a is shorter than side c, if you will. Thinking out loud, low AR1 red noise is in a sense equivalent to a slightly obtuse triangle, so that the attenuation (the ratio of side a to side c) is more pronounced for a given amount of noise (length of side b). You don’t really need a climate model to show this.
I don’t naturally think of the relationship between bristlecones and MBH98 reconstruction as one of signal-noise, but viewed in this prism, the “noise” is RED beyond imagination. Think of noise which is at negative 4 sigma or so for most of its history and then goes to 0 only in the calibration period. The actual proxies violate the assumptions so badly it’s a joke. Ritson probably doesn’t know any better, but Mann does. Drawing attention to the autocorrelation properties of the actual proxies is going to backfire as I think that we’re going to see the ultimate resolution of this ongoing debate arising out of this and sooner than people think.
and wanders into the sunset wondering…………
All this damn statistical hassle over measurements that don’t mean anything. As I have been saying over and over again, tree rings cannot possibly provide a measurable “temperature” signal, when we are talking about a degree C or so. Even if everything is nice and linear. The whole science is a joke.
Oh, re #25, Steve may have another idea, but the first thing that popped into my mind was Kalman Filter. It may not be completely applicable here, but it is still really cool. It is also surprisingly easy to implement when you get past all the equations explaining it.
#29. Yes, I agree with you. Is your argument the same as Osborns and Briffas in their accompanying comment to Storch 04 in Science?
Another point is that Mann seems to be acknowledging that the proxies contain red noise (1-lag correlation 0.3). As far as I know, he rejected this possibility so far. I think they should show their pseudo-reconstructions using MBH98 and their CSM model with red-noise proxies, even with 1-lag r =0.3.
eduardo
#33. I can’t imagine my argument being the same as Osborn and Briffa.
The problem is if you’ve got ONE series with substantial long-term persistence and the rest all white or low-order red noise. I don’t care about the difference between AR1 =0.3 or AR1=0.5 or AR1=0.1. The problem with Mann’s early proxies is that there’s no overall signal.
In your 2004 article, you made some points in passing that I don’t think were properly assimilated – in the pseudoproxies as you constructed them, a simple mean out-performs the Mannian method.
Think about this. First, you have to walk away from one of the viewpoints of Zorita et al 2003 – that you can’t assign the effect of individual proxies. You can. The Mannian method is a multivariate method that, at the end of the day, assigns weights to the individual proxies to make a linear combination. We mentioned this as long ago as our 2003 article but it wasn’t noticed. Burger et al 2006 show a form of linearity, but they haven’t got it quite right. Anyway, the more the weights are equalized the closer you get to a mean.
The nondetrended calibration works “better” than the detrended calibration only because the weights are closer to being equal – it’s kind of like a reverse ridge regression. But if the logic is just to get close to the mean – why not just use the mean? But when you apply a mean to MBH proxies, you don’t get a hiockey stick.
Your 2004 article describes properties of a Mannian type reconstruction if the noise is white noise (or low red noise). BECAUSE the actual results diverge from this, this shows that Mannian proxies do not meet the assumptions of the model. I know that we’ll see lots on realclimate about the “average” autorocorrelation of the 112 proxy netowrk – watch the pea under the thimble – he’s no longer talking about the 70-series North American network – the KEY series which you CAN’T throw out. Why can’t you throw it out if it’s robust? Because the PC1 has huge autocorrelation. I’ll post up the ACF later today.
Mann is starting to remind me of Ted Knight’s character, Judge Smails, on “Caddyshack.”
I noticed a real tear-jerker over at RC this morning from a Glen Fergus…”Why is it that Mann attracts such elaborately contrived criticism?”
#34
Steve,
Ok, I see your point and I also acknowledge that now I would not blithely assert that the effect of a single proxy cannot be assigned. It is a point of which I am unsure, but I would give you that you could perhaps formalize it in terms of a generalized inverse matrix or something similar.
But stepping back to your bristle cones: imagine that I would like to test your argument in the ECHO-G world. I would have a problem in trying to implement everything and at the end of the day identify which is the source of problem (in the case that there is just one source). Should I produce proxies in which the level of noise and the form of their spectrum is drawn from one distribution? which distribution?
I would interested in having your and anyone else´s opinion, since this could be useful for testing other methods, not just MBH.
Eduardo, I’m working on this and some other things, which I’ll send to you for discussion.
#36. I’m 99.99% confident that I can show that the Mannian regression method (after the PC calculates) is identical to Partial Least Squares as practiced in chemometrics. I’ve spend the last week or so buried in multivariate linear algebra, trying to pretty up this insight, and as usual, finding many interesting tangents. Burger et al proposed a formula based on a Moore-Penrose inverse, but I don’t think that they’ve got the linear algebra “right” in the sense of replicating Mann.
Having said that, a point that both they and I agree on is that the Mannian PCs are linear combinations of the proxies. Since the NH temperature index is a linear combination of the reconstructed PCs, the index is also a linear combination of the proxies. You can take it back one step. The tree ring PCs are also linear combinations of the underlying tree ring series, so you can decompose the final index as a linear combination of the proxies. I posted up an interesting graphic a couple of months ago in which I worked out these weights and then showed the accounting by proxy*continent (bristlecoens as a separate class) so that the absolute contribution of each class was shown. You can see that contributions from all classes except bristlecones are negligible. I’ll look up the link and add it in.
Excellent debate / discussion here between Steve M and Eduardo! This is real science! Constructively building upon foundations, testing variations, looking at the results, with no ideological agenda aforethought. Hurrah! A whole new structure, a virtual University. One of the best things I’ve ever done was to check out this blog.
Thanks, Steve. I will certainly heed your comments.
Unrelated to this, but interesting for me, was the comment posted in RC today by Eli Rabett, on the climate sensitivity implied by the MBH98 reconstructions. This has been analyzed by Hegerl et al in their last paper in Nature- see their Figure 3, which seems to me quite clear. As the MHB98 variations are the smallest of all reconstructions, the MPH-implied climate sensitivity (temperature change due to doubling CO2 concentrations) is about 1.2 K. This lies in the very low end of the IPCC range, and would mean almost a harmless anthropogenic climate change. The only possibility to by-pass this (for RC) inconvenient result is that the solar variations in the past millennium should have been minuscule, much smaller than the range quoted in the IPCC TAR.
Ironically, all those who believe in a high climate sensitivity should see, according to Hegerl et al, MBH98 with suspicion. But in reality it is the other way around..
eduardo
Presumably it would be possible to calculate the Ritson autocorrelation for Von Storch’s generated series. This might show whether Ritson’s analysis has any worth at all in showing that Von Storch’s series is unrepresentative of the actual data.
#40. Eduardo, I think that the issue of “efficacy” of different forcings is an interesting one and by no means as closed as people might think. If you do not assume that the efficacy of solar forcing is the same (or even close to) as the efficacy of infrared forcing – with the infrared forcing have less impact for the same wm-2 – and one can contemplate reasons why shortwave radiation of the same energy might have different properties than longwave radiation, then there is a much wider range of potential results. Some studies linking solar to temperature change were considered and repudiated at the time of IPCC SAR on the basis that they implied different forcing consequences for two classes of radiation. I’m planning to re-examine these studies. I’ve got a few ideas along this line and might post up on them in a month or two.
#40 I have been tinkering with the figures from Hegerl (just to see what the Brainiacs in Oxford are up to) and its really clear that solar forcing is responsible for the bulk of the sums of squares in the regression with most of the reconstructions (except ones like MBH that show virtually no response to solar signal).
I don’t think it makes sense to blend them as Hegerl has done into a new reconstruction. One is going to be more right than others, and if model fit is any guide, its going to have significant solar signal, not like MBH98. The estimate of where CO2 sensitivity fits is a side issue as its highly uncertain anyway.
Steve M
What were the two classes of Radiation?
Re#40,
I agree, that’s quite interesting!
Re #40,
Dr Zorita, what you say about climate sensitivity based on several reconstructions is only true if climate sensitivity for solar/volcanic forcing is (near) the same as for GHG/aerosol forcing, as most climate models have implemented. But there are specific differences: solar and volcanic have their largest influence in the stratosphere, including changes in jet stream position and cloud/rain patterns, and solar changes induce (inverse) cloud cover changes (as proven for the past two solar cycles), which reinforce small changes in solar radiation…
As the pre-industrial explosive volcanic emissions have in average not more influence on temperatures than 0.1 K cooling, any residual variation (0.1 K for the MBH98/99 reconstruction, 0.7 K for Esper and Moberg, up to 0.9 K for Huang’s bore holes) is mainly from natural (mainly solar) variations.
As the result of all climate models need to comply with the temperature record of the past 1.5 century (a necessary, but not sufficient condition!), that implies that a higher sensitivity for solar in the pre-industrial world (to be met in current conditions too) need to be compensated by a reduction of the sensitivity for the GHG/aerosol tandem, especially to reproduce the 1945-1975 (cooler) period…
I suppose that it was that what Esper e.a. had in mind in their opinion piece in Quaternary Science Reviews (J. Esper, RJS Wilson, DC Frank,A Moberg, H Wanner and J Luterbacher, “Climate: past ranges and future changes,” Quat. Sci. Rev. 24, 2005):
This is besides the current (very intersting!) topic, but I suppose that some attribution experiments with higher solar sensitivity (without any restrictions like a fixed influence of aerosols, as was done in the Stott ea. experiments) would be interesting…
#42 Yes, the question whether the climate sensitivity depends on the nature of the proxies
is open, but I would say that the standard assumption so far is that this is the case (e.g. Boer and Yu, Climate Dynamics, 21, 167(2003), and it is explicitly used in many energy-balance-like models, as the one used in Hegerl et al (Nature,2006) or in the model MAGICC Osborn Climate Dynamics (2006). It could, however, not be so and some recent papers point to this possibility (e.g. Tett et al, Climate Dynamics 2006) and others that I do not have at hand now.
I was just trying to point out the inconsistency, in the standard “IPCC” setting, between the estimated sensitivities, past solar forcing and MBH98. If the sensitivity is independent of the forcing, one of these three estimations (or ranges) will be wrong.
#46. I would say that only the simpler models (e.g. energy balance models) implement a
forcing-independent sensitivity. GCMs, on the other hand, are free to react differently to solar or and CO2 forcing.
I also think that 0.1K for explosive volcanic eruptions is somewhat too low: Pinatubo for instance will be closer to 0.5K than to 0.1K, but on the long-term the issue remains as to which eruptions are climatically more effective, the smaller and more frequent or the larger and more infrequent. Some recent papers seem to indicate that the former is more probably the case.
A reassessment of past solar variations will certainly have consequences, in one or the other direction. I am not sure now if, for instance, a very small past amplitude is compatible with the secular changes in the 20th century, since the simulations for the last 150 years (e.g. Stott et al.) “need” this forcing to replicate the observed temperature evolution. If solar variations were indeed smaller, then natural unforced variability in the late 19th century and early 20th should be larger. And if larger before why not larger at present also? So, I think this avenue of small past solar variations could also be dangerous for mainstream IPCC.
In any case, what surprises me is the level of attachment of mainstream IPCC to MBH98, since within this framework Hegerl et al is quite clear: MBH implies a climate sensitivity of about 1.2 K. This does not seem to have risen many eyebrows. Probably I have overlooked something.
eduardo
#47. I get your point in the results of MBH. My guess is that this is another example of ‘moving on’. To summarize, it seems that the relationships of structual aspects of the models vs estimates of sensitivity seem fairly open. I think this is particularly so given the small time interval that GHGs have been above baseline relative to the reconstructions time interval. Secondly in the regressions I have done using the Hegerl data it is interaction terms of solar with GHG and aerosols that dominate, not direct solar effects, even in producing the clear signal of solar effects throughout the reconstructions. I am suspicious the systems of equations are ill-conditioned but am searching for a way to clarify what interaction means in this context.
I would also add that some component, perhaps a large component of AR(1) behaviour might come from the sun, and so provide a source for parameterization of redness in simulations.
Is this post about a reconstruction or about a PC1. The extent of the three card monte games is starting to be dishonest, Steve.
#49. Look, I’m getting tired of this. Every graphic is that article is a “reconstruction”. A Mannian reconstruction is just a linear combination of proxies. In this case, we did it with “pseudoproxies” only constructed differently than VZ. Our pseudoproxies were one PC1 and 21 white noise series, combined into a “reconstruction”. So please stop this crap.
Please correct me if I’m wrong, but isn’t the color of the noise perturbation entirely irrelevant in the context of pseudoproxies? – The regression model is invariant under a (common) reshuffling of the x,y series, so given one performance result, you get the same answer with reshuffled, i.e. white noise perturbed, series.
The only crucial parameter (besides the usual suspects such as x-y nonlinearities) is the noise amplitude, in other words, the signal-to-noise ratio.
Am I wrong?
#51. Gerd, yes, I think that you’re wrong. What neither you or Eduardo (in my opinion) are adequately considering is what “noise” would look like for series that were not actually temperature proxies, but representing something completely different.
I think that I’ve had somewhat of a communication gap here as I don’t approach things from a “signal-noise” model. The concepts of statistical relationships in economics don’t start with the assumption that there is “signal” and “noise” and the premise is different. You reject hypotheses. In the Mannian multiproxy world, nothing is ever rejected; everything is dumped into the bucket in the hope that somehwere in the covariance matrix, you get a relationship to some climatic field. When you have 11 “climatic fields” and hundreds of proxies and a calibration period of 79 years and huge autocorrelation in some proxies, it’s a recipe for disaster.
In econometrics, it’s established (for example, Ferson et al 2003) that there is an interaction between autocorrelation and spurious regression. Deng (2005) has noted that ARMA(1,1) processes with high AR1 and high negative MA1 have the property of being “almost integrated almost white” and pose some very intricate issues for statistical testing, which I’m pondering and am still studying. Since ARMA(1,1) is a very strong feature of climate series – much more so than AR1, there are lots of intricate issues.
But to bring it back to the signal-noise problem, I think that the way that I would communicate this in signa;-nosie terms (and I’m still playing with this) is that “key” Mannian proxies – the ones that you CAN’T “throw” out are “red” beyond anything that you’ve ever contemplated i.e. at negative 3 sigma or more for centuries. Is it useful to think of this even as a “signal”? I don’t think so, but having said that, I’m trying to express this concept in signal-noise terms that will perhaps be more accessible to practitioners.
Steve, much of that referenced POST’s discussion was about the shape of the PC1 rather than the shape of the reconstruction. Yes, there is an article referenced within that post. But I’m asking about the discussion IN THAT POST. Given, the past sins by you and Ross on conflating PC1 impact versus impact in the reconstruction*, I think I’m justified in asking clarifying questions where recurrence is possible.
*In discussion, old chap. Not in your EE article.
#52. Steve, you are 100% correct with the problem of autocorrelation and d.o.f. and the like, but that doesn’t answer my question(s).
My point was different, and you really have to think in terms of S/N here, as we are talking about noise perturbed pseudoproxies.
Just imagine the simplest case with one proxy x and one temperature record y, and some deeply red noise “between” them. The regression model – and its adequacy – is solely determined by Cov([x,y]), which is, under normality, the shape of the x-y point cloud. The noise enters this picture through the spread of the cloud, that is, the amplitude of the noise series. Now there is no time coordinate whatsoever, and if you run the experiment with another noise realization (of equal amplitude) – which is by definition totally uncorrelated to x and y – you should get the same picture if you run it long enough. That cloud doesn’t care whether the noise was from a brown, red, or white noise process.
No?
Gerd, let me think about what you said, I’ll try to back to you tomorrow.
#51, #52, #54, #55:
Maybe this will help.
The redness of the noise matters very much. To put this in regression terminology (I’m sure there is an analog in S/N terminology):
In the OLS regression y = a + bx + e, the errors, e, are assumed to be i.i.d. and independent of the x variables, or to put it another way, the covariance matrix of the errors terms is assumed to have ones on the diagonals and zeros everywhere else.
Redness in the error term violates these assumptions and screws up the inferences you can draw and may bias the estimate. Redness means that the off-diagonal elements of the covariance matrix are non-zero. VERY red noise terms means that a lot of off-diagonal elements are non-zero and the OLS confidence intervals will be greatly understated. To correct for this, you need to do GLS and impose some structure on the covriance matrix. If the error terms are correlated with the x values, then OLS gives you biased estimates.
See http://courses.washington.edu/hserv523/pptfiles/olsmlvio.ppt#9 for the OLS assumptions.
I hope this helps … or maybe I just misunderstood the question and this is off-point.
#54 I think you have missed or confused the point that the temperature record can/has be modelled as a stochastic process or colored noise. If you look at ClimateAudit post august 13 2005, Steve has modelled satellite data and gridcell temperature as ARMA models with high AR1 coefficents in the .7 to .92 range.
GLS assumes that there’s AR1 structure.
Once you get past the PC questions, the MBH reconstruction boils down to a regression of the temperature PC1 against the proxies (all 22- 112 of them) over a 79 year calibration period. Most regressions even multivariate go cause to effect. Here he’s regressing temperature against tree rings.
Most multivariate methods are concerned about collinearity. That’s no problem in the early neworks !?! The proxies are all nearly orthogonal to each other. This presents a problem for “signal-noise” models if your job is to detect a signal from 22 nearly orthogonal.
One of the big differences in signal-noise people and economics people is that the signal-noise people assume there’s a signal (it’s just that it’s very faint and it may have a lot of “noise”) whereas an someone from an economics viewpoint would say – That’s a dead parrot.
Slightly off the thread,but,wondering about CO2 fertilisation effects and Briffa’s modern-day ring width ‘excursions’ – could one do a reconstruction of the past temperatures that started with first differenced temperature and proxy series?
I was thinking that if a tree ring series really responded to temperature then not only would the raw series correlate but so might the first differences -but perhaps this is wrong?
#59. Chas, there’s a very interesting analysis of first differences in MBH98 on another blog that I’m going to post a link to later today. The author concludes that the first differences of the MBH reconstruction are white noise.
#56. I guess you are talking about the estimation problem, where autocorrelated errors are certainly an issue (although I could not follow your OLS characterization – simply think of the 1-dim case with no off-diagonals). But the original v. Storch 2004 question was: how to perturb simulated temperature records with noise to generate realistic pseudoproxies. This is totally different, and my claim still is that here the color of the noise is irrelevant.
Maybe Eduardo has some comment on this?
#54. Gerd, the issues that I’m thinking of are the problems of spurious regression as set out in Granger and Newbold 1974 and Phillips 1986, which I’ve posted on here. See spurious regression category. If you calculate the covariance between two random walks, you get spuriously high covariance values. Phillips showed that the t-statistic does not settle down as N increases, but diverges.
Phillips characterized “spurious regression” as situations where the t-statistic didn’t converge (which makes covariance based methods unreliable). This has been extended past two random walks to random walk plus a deterministic series, two fractional difference processes with d1+d2>.5, etc.
For series with high autocorrelation (say AR1>0.9), under some circumstances, their finite sample (say 50-80) behavior is more akin to random walks than to low AR1 red noise, although given a long enough N, they settle down. If you have a combination of high AR1 (>.9) and moderate to high negative MA1 (-.4 to -.7), you can get noise that is “almost integrated (i.e. almost random walk) almost white” and most statistical tests for whiteness etc. have low power against this form of noise. Given that actual gridcell temperature series can be much better characterized as ARMA(1,1) than AR1, this poses many interesting and difficult statistical problems that barely seem to be on anyone’s radar screen. The literature (e.g. Perron) gets very difficult very quickly.
#56 Terry,
You said “Redness in the error term violates these assumptions and screws up the inferences you can draw and may bias the estimate.” Redness — here interpreted to mean correlation between the error terms in different periods — does mess things up a bit, but it does not bias the OLS coefficient estimators. Increase the variance of those estimators: yes. Bias, no. (This is essentially Gerd’s point in $51 about mixing the chronology of the sample if I understand that correctly.)
Of course, bias may not be all that important. If we were shooting at a bull’s-eye in one foot target and had a one inch bias to the left, that is one thing. If our variance is so big we can’t hit the side of the barn the target is on, that is another. Hence hitting the barn is the reason that econometrics is full of techniques (which have other costs) that reduce the serial correlation. Note, the classical spurious regression (of Yule or Granger and Newbold) is not a case of bias. Rather it is a case of very large variance in the OLS estimators due to the high (or perfect) first order serial correlation: the spuriously significant coefficient has equal probability of being positive or negative. However, if you use these (spuriously significant) coefficients in a subsequent calculation that effectively flips the sign of one or the other, then that result is biased.
So to return to Gerd’s question in #54, the results in reconstructions (because they are based on a sequence of relations using the covariance) probably do depend on whether the errors were “from a brown, red, or white noise process.” Maybe somebody can figure out the bias by analytical (i.e. solving the distribution equations of the various estimators taken into the collective temperature reconstruction), but it looks intractable to me. Thus, one has to resort to experimental means: reconstruct the reconstruction algorithm and simulate various types of temperature and proxy series to correspond to the varying assumptions of the underlying distributions.
Maybe I can make the importance of this last point clearer by noting a subset of the MBH98 reconstruction: the data transformation and PCA technique used on the N. American tree ring network. MBH say the hockey stick is what nature has shown us. MM say that the MBH98 hockey stick is (among other things) a consequence of the transformation and PCA taken on the then transformed data. If the tree rings have no serial correlation (not to say they don’t), then MBH are right. If the tree rings show only a first order autoregressive process, AR(1), with randomly selected coefficients from 0.0 to 0.99, then MBH are still right although the relative rates to find hockey sticks show a different (but on such small levels that it doesn’t mean much). But go to a third order autoregressive-moving average and MM are right. Hockey stick creation becomes significant in any PCA and much more likely with an MBH98 process. Make a few series random walks, then MBH98 almost always finds a hockey stick by the PCA finds many but nowhere almost always, i.e. MM are right. With almost all series modeled as random walks, hockey sticks will abound regardless of technique. (Steve and Ross simulated with an ARFIMA — autoregressive fractionally integrated moving average — model using the estimated correlogram of tree ring network.)
The whiteness or redness or whatever of the underlying process makes a difference. And while the statistics of time series is messy, cheers — make that three cheers, it can be really messy stuff — to Steve for exploring the consequences the time series assumptions in public.
#61. Gerd, I submit that the process that we used in our GRL article to simulate pseudoproxies was more sophisticated better than anything that von Storch and Zorita used, which is why our simulated hockey sticks looked so realistic.
We modeled the tree ring series using fractional differenced noise models (Hosking) which yield long-term persistence. Demetris Koutsoyannis has a nice model for creating long-term persistence through creating noise on multiple scales. I don’t know how to implement this in a simulation, but David Stockwell might know.
We also did Mannian principal components on these series and produced all sorts of interesting looking “pseudoproxies”. From your point of view of each of these things could be considered as “noise” to be added to a signal which your challenge is then to extract. The breakdown points are quite different than for white noise or for AR1 nnoise.
These are also just noise processes. The other situation that needs to be modeled is making pseudoproxies from unrelated things. Eduardo’s sent me their precipitation data and realistically one should make pseudoproxies using combinations of precipitation and temperature data. You then need to add nonlinearities. That’s one set of issues.
Mandelbrot wrote about tree ring series as having properties like those of fractionally differenced series nearly 40 years ago and reported on earlier editions of some of the tree ring series in Mann’s North Amrican network, so this viewpoint has an eminent pedigree. That;s another set of issues.
I’ve experimented with perturbing signals with networks of this type of noise and the breakdown point for signal recovery is pretty interesting. For example, if you do principal components or biased Mannian principal components or merely take an average, you recover the signal from medium-sized networks with signal-noise variance ratios down to 0.2. The Mannian method starts breaking down the earliest. Its tendency to mine for hockey sticks competes with recovering the signal and between 0.1 and 0.2, the hockey stick emerges in all its glory at the expense of a real signal.
A third set of issues is what happens with completely extraneous “signals”. I’ve tested this empirically by doing inserting things like dot.com stock prices into a data set of dendroclimatic indicators and seeing how things work. Are the methods resistant to outliers? Empirically I’ve found that under Mannian methods, dot.com stock prices plus white noise, dot.com stock prices plus actual proxies other than the NOAMER PC series, the NOAMER PC1 plus white noise and the NOAMER PC1 plus the other proxies all produce nearly identical reconstructions all with RE statistics in the 0.4-.5 range and verification r2 statistics of 0. There’s definitely a moral in this experiment.
#65. There’s another interesting time series phenomenon from ordinary PC that I noticed while I was experimenting. If you take the (not-Mannian PC1) of red noise, it finds low-frequency variability that isn’t in the data. I’ve never seen anything like this reported in the literature.
Because the PC process can assign positive or negative signs, the eigenvector 1 ends up in a noise situation with half the series flipped. The impression that I get is that it tends to create a wave with a period about half the length of the data set i.e. 2-3 cycles and builds up spurious energy in that wave length. I can sort of see how this would happen in a variance maximizing process and that a calculus of variations specialist would probably know how to prove it – maybe it’s already been proved somewhere. But it’s a neat mathematical phenomenon. It doesn’t occur in an averaging situation or in a situation where coefficients are constrained to be positive because it depends on the ability to flip series.
One other thought along these lines. After the PC calculations, Mannian methods boil down to a type of poorly understood linear regression of the temperature against the proxies. This point is either not clearly understood in the general community or denied, although Gerd and I both agree on this. Because there is so little actual signal in the data, there is surprisingly low collinearity in the regressors and the regression is not as far away as all that from a multiple linear regression of temperature on 22-112 proxies over a calibration period of 79 years. (In the 112 proxy situation, its not a perfect fit because they use what is equivalently partial least squares rather than OLS, but the fit sitll yields a very high calibration r2).
Can you imagine an economist taking residuals from a model fitted this way, taking twice the standard error of the residuals and calling it a 95% confidence interval?
Aside from this, I think that people really need to think through what the physical meaning of multivariate regressions of temperature against proxies is. Here’s what I mean. Another "model" for what we’re doing here is creating a portfolio. Instead of thinking about regression coefficients, think about weights in a portfolio (it works out the same, its’ just that you think differently about it, or at least I do.) You stop thinking in terms of a portfolio being "right".
Now think about the extremes in portfolio management – and this is a point that I’ve been mulling over in context of the dispute between VZ and Wahl et al over detrending, which I’ll tie together some time. If you can’t have any short sales, then your portfolio is "bounded" in a sense. You can load 100% on any one of M stocks (proxies) or at the other extreme, you can have an arithmetic average of them. Multivariate methods with positive coefficients are constrained to this simplex of coefficients. You tell me why something on the simplex is "right" or what the meaning of a confidence interval is. The tree rings are not "causing" temperature.
This implies that strategies are also bounded: in effect, you can try to pick your "best" proxy and go 100% on that or go with an average.
In effect, Mann goes with the bristlecones. Everything else is pretty much for show. That’s the portfolio that he picked on the simplex. His multivariate regression method – PLS – tends to prefer concentration in the portfolio to balance, if I can put it that way. So the portfolio is loaded up with bristlecones. We’re coming full circle here – it really is a dot.com investment.
One other thing – if you allow for short sales in a portfolio (i.e. negative weights) the range of portfolio management becomes huge. There are some articles about this by physicists of all people, if you google noisy covariance matrix portfolio also with spin glass – you’ll find some curious articles which bear on this. B and C 2005 has only touched the surface of the range of results from noisy covariance matrixes where there is no control on sign of the coefficient.
The whole debate between VZ and WRA has completely grabbed the wrong end of the stick – by all parties. In the VZ situation, a simple average of pseudoproxies out-performs either the detrended or nondetrended calibration. I noticed this for myself, but it’s mentioned, buried deep in VZ04. Why does nondetrended outperform detrended in the VZ situation? Because the coefficients are more "balanced" i,e, closer to being a simple average. Nothing more than that. Doing a regression with inclusion of a common trend draws all the coefficients towards the mean. It;s exactly the same effect as if you did a bizarro-version of ridge regression – instead of as in ridge regression, you get the reverse effect if you do
as in ridge regression, you get the reverse effect if you do 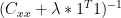 , which I’m calling "smudge regression" in my head. I’ve not seen this discussed anywhere, but if you carry "smudge regression" to the limit you get the coefficients of the mean (1/N) as your "regression coefficients" which is sort of interesting. Mann’s partial least squares carries ridge regression to one extreme, the mean is what happens when you carry smudge regression to the limit.
, which I’m calling "smudge regression" in my head. I’ve not seen this discussed anywhere, but if you carry "smudge regression" to the limit you get the coefficients of the mean (1/N) as your "regression coefficients" which is sort of interesting. Mann’s partial least squares carries ridge regression to one extreme, the mean is what happens when you carry smudge regression to the limit.
I’m thinking out loud here. I’m sure that something like this has been written up somewhere , but I haven’t seen anything exactly along these lines,
##63,64. Maybe we can agree on the following: The noise color – as long as scaled to a unique amplitude (= S/N value) – has no effect on Cov([x,y]) and the “true” regression model M. For the subsequent estimation of M, color of course matters, as red noise is much harder to sample than white. For the purpose of v. Storch 2004, white noise would have been ok.
If the color gets too dark stationarity is lost, so brown may not be appropriate here (has anybody tested temperature/proxy series for stationarity?). But that is a different story.
Let me try a different way.
The pseudoproxies are all a vector sum of signal and noise. In the simple case of white noise, the noise is orthogonal to the signal and is high-frequency. When you average the pseudooproxies or take some other linear combination of weights through a Mannian regression or some other regression, and then rescale the “length” of the resulting estimator to the length of the original signal, if I can speak that way, the centennial variance in the reconstruction is less than than the centennial variance in the signal because you’ve blended in high-frequency white noise which occupies some of the energy in the re-scaling.
If the noise is not orthogonal to the signal, but say strongly covariant with the signal, then you have the equivalent of an obtuse triangle. There are no general rules for which side of a triangle is the biggest. Low red noise is like something that’s close to orthogonal so you get something close to a Pythagorean effect. I don’t think that there’s anything in the original VZ article (or in the present dispute) that rises above these simple high school geometry concepts.
The attenuation is obvious with white noise. The huffing and puffing of Wahl et al is like arguing against the Pythagorean Theorem. The white noise assumptions fon’t apply to real proxies where the properties are much much worse than what are being talked about by Ritson at realclimate.
Think about what happens if the noise covaries with the “signal” rather than in terms of AR1 and what happens with Mannian rescaling. In the Mann case, the “key proxy” has MUCH MUCH greater low frequency variance than the temperature “signal”. It shows an Ice Age in California for most of the last millennium. The MBH reconstruction is a blend of the California Ice Age with white noise.
1. So what percent of the reconstruction is bristlecones?
2. Isn’t it at least a plausible rationale to favoring proxies more which track during the insturment period than those that don’t?
#61: Gerd
If you use different noise, you get different pseudoproxies, so the redness of the noise does matter. More specifically, red noise will impart redness to the pseudoproxies. At most, you are arguing that the redness doesn’t matter for some purposes, but it is a bit hard to believe that imparting redness to the pseudoproxies is completely irrelevant.
Steve said:
This is one reason redness in the pseudoproxies would matter. (This is basically what I said above about redness of the error term screwing up inference in OLS.)
#63:
Agreed. I was just trying to show off by throwing in the bias stuff.
I was just reading the Ritson post over at RealClimate, and it was a rather surreal experience. Not a peep about all of the stuff here.
I submitted a comment asking about this — very politely of course.
#68.
If it’s not orthogonal (= uncorrelated), it’s not noise. But I assume you are again talking about sampling errors, aren’t you.
Gerd,
I think the color of the proxies is relevant for the following reason:
in a reconstruction excerise you estimate the covariance matrix at high frequencies (with detrended calibration) or at a mixture between high and low-frequencies (with non-detrended calibration. You then assume that this covariance matrix is valid at all frequencies, from high to ultra low. This is, however, not true, since the covariance matrix at very low-frequencies (timescales larger than the noise autocorrelation time) will be determined by physical-processes and not by the noise. If this is true, a model calibrated with low-pass filtered proxies and instrumental record should behave better, provided you have enough sample size. The problem would be to estimate the correlation estructure of the noise. This seems to me to be the critical point in all this discussions.
When using white noise proxies and nondetrended calibration, the signal-to-noise ratio at low frequencies is enhanced with respect to detrended calibration. If you construct red-noise pseudoproxies, where the signal-to-ratio is constant over the frequency range, the covariance matrix does not depend on frequency, but then you are just fitting the noise in the calibration period.
I think this is just what Steve is saying when explaing this effect with the Pithagorean theorem.
eduardo
I think I got it now. It is always better to actually read the papers before commenting them. – Thanks for your patience.
#72. Gerd, you said:
I’m coming at this more from a statistical perspective than a signal processing perspective. I can think of lots of cases and obvious examples.
Take tree rings. Suppose that the “signal” is temperature (leave aside precipitation and fertilization for now) and the ring width has a quadratic (upside-down U) response to temperature. And suppose that you know the signal. The residuals from a linear fit are going to be correlated to the signal.
Or another case. The autocorrelation properties of tree ring chronologies vary sharply by author. The Durbin-Watson statistic for Stahle chronologies as about 2 and for Jacoby is under 1. Let’s suppose that the “signal” presented to the trees examined by both authors had somewhat similar autocorrelation properties. Then the residuals from subtracting the “signal” from the proxy are going to be correlated to the signal.
If you now try to do things on a calibration period of only 79 years, any two trends will be highly correlated – this is the essence of the “spurious correlation” problem. Car sales in the United States are correlated to births in Honduras. In the Mann case, is the 20th century correlation between the bristlecone PC1 and temperature PC1 – which underpins the entire reconstruction and the entire debate beweeen undetrended and detrended – valid or spurious? One indication that it is spurious is by examining residuals, which are not uncorrelated to the “signal” as reconstructed, but which have huge correlation. Also they imply that there was an Ice Age in California for most of the millennium, which is not suggested by other proxies.
I don’t follow the rest of the post, but here want to comment that there is no reason to think of a nonlinearity differently then any other confounding factor. If I do a multiple correlation modeling, it’s just one more factor in the polynomial
Except that they don’t do polynomial fits. They do linear fits.
you don’t get my point, Steve. Having x1, x2, x3…x29 variables all in a multiple correlation model. Now introduce the issue of X1(sq). It can be handled just like x30. It’s just another confounder.
#78. In Davi et al, which I mentioned about a year ago, they propose a quadratic fit to explain the "divergence" factor. Sure it can be done. But you’re talking univariate studies. When you start handling 70 series with principal components or Mannian multiple regressions, they don’t allow for nonlinearities and Mann explicitly excludes it as a very unlikely possibility in MBH98. So yes, I agree that it could be done easily in fitting individual series; just that MBH is entirey linear.
Not just MBH. Moberg’s results rely almost entirely on ignoring non-normal non-linear relationships and that’s an enormous problem with his study that most people don’t realize.
To me, it’s no different than ignoring any other potential confounder. The precip, etc.
OK, but it’s the other guys that are doing the ignoring.
It is easy to test different signal models with Matlab:
% signal
s=0;for i=2:440, s(i)=s(i-1)*0.1+randn;end
% noise
n=0;for i=2:440, n(i)=n(i-1)*0.9+randn;end
% measurement
X=s+n;
% shift one
X2=[X(2:end) 0];
% 1st method
sum(X.*X2)/sum(X.*X)
% diff
Y=X-X2;
% shift one
Y2=[Y(2:end) 0];
% 2nd method
1+2*sum(Y.*Y2)/sum(Y.*Y)
I tried to put the meaning of the above code to equation form, in here. Bad english, maybe other errors too, but the stakes are high anyway.
Source
Steve, (#66)
I’m not sure what our getting at because doesn’t what you term ridge regression also smudge the fit between the parameters if I is the identity matrix. I suppose for what you call smudge regression you could choose a T so that as lambda approached some predefined value the fit would approach the average. This is kind of interesting. For instance if:
T=(-C_xx+(1/n)*psudoinverse(C_xy))
Then maybe as lambda approaches one you would get the average.
Found quite interesting paper, ‘Time Serier Modelling and Interpretation’, C. W. Granger and M. J. Morris, Journal of the Royal Statistical Society. Series A, Vol. 139, No. 2. (1976)
page 250:
Steve:
So, after all, we are speaking about the same issue.
UC, JC, any idea what causes the MA(1) to be
??? UC, JC, any idea what causes the MA(1) to be less than zero?
bender, in one of DEmetris Koutsoyannis’ papers, I don’t recall which oine off hand, he says that if you take period averages of an AR1 series, you get an ARMA(1,1) series, but I don’t know whether this explains the negative coefficient.
Empirically, when you model a say ARMA (.92,-.45) series as an AR1 series a la Ritson/Nychka,… a la climate scientist, you tend to get AR1 coefficients aroung 0.4, which underestimates the true autocorrelation.
Deng 2005 calls these series “almost integrated almost white” – a class studied by Perron 1992 or so.
If you get a specific Koutsoyannis citation, I’ll read it. We may be in agreement – a MA(1) when you model a say ARMA (.92,-.45) series as an AR1 series a la Ritson/Nychka,… a la climate scientist, you tend to get AR1 coefficients aroung 0.4
Sure. Any model mis-specification is going to lead to a bias in parameter estimates. Not unlike fitting a linear calibration to a nonlinear temperature response curve.
I think it is important to realize though that the AR1 term is not due to an underlying autoregressive short-term climate-memory process. It is the result of a trend (or low-frequency noise signal). Remove the trend and the AR1 term disappears.
The AR1 could be the result of an autoregressive forcing process (solar, CO2, etc) – but even in that case the model is still mis-specified, as it is not the dependent variable that is autoregressive, but some exogenous agent that hasn’t been included.
Grrr. Not sure why this didn’t post correctly. I repeat:
Sure. Any model mis-specification is going to lead to a bias in parameter estimates. Not unlike fitting a linear calibration to a nonlinear temperature response curve.
[etc.]
Oh for crissakes the first half of #89 is screwed up as well. (I think the problem is my “less than zero” symbols). I repeat:
If you get a specific Koutsoyannis citation, I’ll read it. We may be in agreement – a MA(1) less-than-zero term can be expected if you are taking naturally quasi-cyclic data and splitting it at arbitrary time-points. This is what I mean by “framing bias”.
bender – it might be a little more than just trend or low-frequency. If you simulate ARMA (.92,-.45) or such, you get series that generically look somewhat like temperature series. But your point is well-taken and Koutsoyannis has made much the same point, although his concept is persistence on different scales – which I instinctively like as a concept, however, without fully undestanding its practical effects or properties. I’ll post up some Koutsoyannis’ refs. David Stockwell has some discussion of Koutsoyannia as well at his blog and is more familiar with his ideas than I am.
This sounds like a good model to me (this is not the first time it’s been mentioned here; I’ve been paying attention), and I’m interested. Persistence makes sense when you’re talking about slow-churning stochastic dynamic systems with elements (e.g. oceanic currents) that are transient and/or yet to be characterized.
I’m not a climatologist. But I have to wonder about the fluid dynamics component of the GHG/AGW debate. Currents expel a heck of a lot of energy. And what we take as “fixed” could easily be stochasticity on a time-scale that is slow relative to the human attention span. I wonder how GCMers decide which effects ought to be considered transient and which ought to be considered persistent. If the earth is a “nonlinear terawatt-scale heat engine” large portions of it may be functioning far from any computable equilibrium. In which case what seems persistent today may be transient tomorrow. (If a current were to shut down temporarily, you’d necessarily get a transient warming effect.)
[/musing off]
RE: #93 – I wish I had the time to dig into the models. I get a very strong sense that they fail to adequately integrate all of the mechanical work going on in the atmosphere and at its interfaces with the surface. Just a hunch ….
I think UC might be on the right track for the negative MA coefficient because I can’t see any reason why high altitude trees should respond negatively to temperature. Consider a tree that has a partial fraction expansion of the z domain transfer function between temperature and tree growth as:
G(z)=T(z)/u(z)=1/(z-a)+1/(z-b)
We see that that there are two states affecting tree growth and both states respond positively to temperature. When we put this transfer function in numerator denominator form:
G(z)=(2z-(a+b))/((z-a)(z-b))
Thus we do get a negative moving average term but if a and b are both less then one as they should be for stable zeros then the tree still responds positively to increased temperature. To test this hypothesis, we should use an arma(2,3) model.
bender:
Don’t know. Overshooting control system?
Not sure if I understand what you mean. In general, if there is a forcing that we are not aware of, AR-model would be the simplest way to model it. It gives some means to predict the future and reconstruct the past (using noisy observations). Here, in the proxy case, positively correlated noise means that averaging won’t cancel the noise as efficiently as it would cancel uncorrelated noise. That’s why they want to show that noise is not positively correlated.
Granger’s paper continues:
This is really interesting, how ’bout signal is white and proxy noise AR1 ? 🙂 ..I just don’t get it why they don’t subtract known thermometer reading from the individual proxy data, result should be the noise term. No need for Ritson’s method then.
UC, I think that you can’t distinguish between an ARMA(p,p) and an AR(p) plus white noise if you are talking about a noise model but I think the case is different if you are talking about a system where you can measure the input. Personally for a noise model I do not see the point in distinguishing between an ARMA(p,p) and an AR(P) plus white noise. The transfer functions are the same so in my mind they are the same.
#97, yes, can’t distinguish. That’s what Granger proofs. So, even if we know that the system outputs an ARMA(1,1) process, we can’t tell how the system generates it. We have to observe the input as well, otherwise the noise identification is impossible. Local temperature is the input, and proxy is the output. Proxy minus temperature is the noise process. At the calibration phase this is observable. But the method introduced at RC is different:
They don’t use proxy minus temperature, they assume that signal is slow. If this assumption does not hold, the method is invalid (here’s why) . If it holds, it still would be easier to just remove the signal and use traditional AR estimation technique.
BTW, if the signal is slow, it means that we can take any location, and predict very accurately its annual mean temperature for the year 2007.
Re 93, bender, you say:
Have you read Thermodynamic optimization of global circulation and climate? (Adrian Bejan and A. Heitor Reis, Int. J. Energy Res. 2005; 29:303–316) It is a fascinating study of this very situation, using the Constructal Law to develop the shape of the climate system from first principles. The Constructal Law has a number of implications for the study of climate, some of which are discussed in this paper.
The Constructal Law, in fact, applies specifically to flow systems, i.e., those systems which are far from equilibrium …
w.
# 87
One simple model for negative MA1: High-pass filtered white noise, for example 1st order Butterworth with cut-off frequency 0.2; AR coeff 0.51 and MA -0.76.
By googling I came accross this 1990 paper: Woollons & Norton: TIME-SERIES ANALYSES APPLIED TO SEQUENCES OF NOTHOFAGUS GROWTH-RING MEASUREMENTS.
Does anyone know if the studies cited (see summary in Table~3) examined any chronologies used by the Team? Especially the paper by Monserud looks very interesting (unfortunately I do not have an access to it).
Another related, and possibly interesting old article from google scholar: J. Guiot: ARMA techniques for modelling tree-ring response to climate and for reconstructing variations of paleoclimates.
# 101
thks, interesting paper. Just noted that there are different conventions for the signs of AR and MA coefficients. Need to be careful.
Still looking for a proxy record along with a nearby temperature record, would help a lot.
‘If proxies high-pass filter the temperature signal, the residuals will be red’
I wrote:
Amateurish me, MBH98 says that my search is pointless. Do they have FAQ at RC? Would like to improve my understanding of these assumptions of MBH98:
If climate is average weather, how can global and local phenomenon be uncorrelated? Does thermometer reading represent a local or global climate phenomenon?
Does this sentence include an assumption that sudden, large variations in the past are not possible?
What do teleconnections mean in this context?
#104. Actually, I’ve discussed a number of individual proxy examples comparing MBH proxies to gridcell results.
In our Reply to Von Storch, we compared gridcell temperatures to MBH tree ring chronologues and showed a histogram of 70 correlations which were nearly all negligibly different from 0.
I’ve done even more specific studies of bristlecones and foxtails as used by Esper and Osb-Briffa. A Weather station operated from 1951 to 1982 about 10 km away from Sheep Mountain, the most heavily weighted site in both the NOAMER PC1 and in MBH (And which has a distinct HS shape). It has 0 correlation to temperature. Christy recently did a big collation of Sierra Nevada temperature informaiton and there is a slightly negative correlation between bristlecones and Christy – which I presented in our 2nd House Energy and Commerce presentation.
When we criticized MBH for the lack of correlation to local temperatures, they produced this argument that there was a teleconnection correlation. Thus, because bristlecone growth increases in the 20th century and because NH temperature increases in the 20th century (trhus the temperature PC1), there is a correlation between the two of these. This point of vie is re-iterated in Wahl and Ammann.
They do not consider the possibility of spurious relationships occurring through data mining. I’ll post up some scripts on this if you like (though I’m really pressed for time.) You’ll also need to download the CRU temperature data into a usable form. I’ve posted up a script in R to make an R object of the CRU data set and you really need to have this data set handy and callable.
Thanks, found some related older posts. A figure with temperatures on x-axis and proxy readings on y-axis would help to visualize the correlations. IMHO there is a fundamental flaw that brings up the teleconnection argument, assumption of slow signal (Ritson coefficient) and MBH99 2-sigma levels. Either this flaw is in their methodology or it is my interpretation of it.
Intensive course to the problems of MBH9X:
This sentence of MBH98
and
MBH99 Figure 2.
In Mann et al, Climate reconstruction using ‘Pseudoproxies’, GRL Vol 29, No 10. (2002), Figure 1 clearly shows that the signal is not ‘slow’. They should try the Ritson’s method with that data. In addition, this paper claims that red noise does not matter:
(actually, to be honest, I can’t figure out what the above sentence really means..)
BTW, with the assumption of slow signal, the Ritson method gives 1 for random walk (there is a 0/0 in the derivation in this case, but still). I think that the random walk case plays no role in this fiasco.
This just came in I think that the fight is over in no time. Where can I place my bet?