I thought that some of you would be interested in a plot of Juckes’ Union proxies against gridcell temperatures. I’ll start off by simply showing a plot during the 1856-1980 calibration period (both scaled over 1856-1980), as below, followed by a plot of the residuals. The proxies are arranged according to longitude from California going east to China, going down columns first. The prefix in each legend is the multiproxy source; the suffix is a short version of the proxy.
Plotting data is one of the first things recommended in statistical studies and its absence is quite notable in the Juckes study. These simple plots raise many questions.
Figure 1. Juckes’ Union proxies 1856-1980 (calibration period). Black – proxy; red- CRU gridcell. Both scaled in 1856-1980 period.
Next here is a plot of the residuals from the series illustrated in the above graphic.
Figure 2. Residuals between Juckes’ Union proxies 1856-1980 (calibration period) and CRU gridcell temperatures, both scaled in 1856-1980 period as in Figure 1.
Third, I’m going to show a table listing the correlations of the above 18 proxies to gridcell temperature and to the NH temperature version used by Juckes – together with a code showing the gridcell number of each series (indicating whether any proxies are in the same gridcell).
|
other_name |
id |
jones |
cor.grid |
cor.nh |
|
|
5 |
Upper Wright (USA) |
ecs.upp |
733 |
-0.02 |
0.46 |
|
34 |
Methuselah Walk (USA) |
mob.mw |
733 |
0.15 |
0.15 |
|
1 |
Boreal (USA) |
ecs.bor |
733 |
-0.01 |
0.35 |
|
33 |
Indian Garden (USA) |
mob.ig |
733 |
0.13 |
0.04 |
|
39 |
Chesapeake Bay: Mg/Ca (degC) (USA) |
mob.ches |
741 |
-0.05 |
-0.16 |
|
30 |
Quelcaya 2 [do18] (Peru) |
mbh.queo2 |
1462 |
0.35 |
0.37 |
|
31 |
Quelcaya 2 [accum] (Peru) |
mbh.quea2 |
1462 |
-0.14 |
-0.14 |
|
38 |
GRIP: borehole temperature (degC) (Greenland) |
mob.grip |
245 |
NA |
0.68 |
|
16 |
Crete (Greenland) |
jbb.wgr |
245 |
NA |
0.14 |
|
27 |
Morocco |
mbh.morc |
827 |
0.11 |
0.13 |
|
4 |
Tornetraesk (Sweden) |
ecs.tor |
329 |
0.27 |
0.31 |
|
14 |
Northern Fennoscandia |
jbb.tor |
329 |
0.46 |
0.28 |
|
42 |
Arabian Sea: Globigerina bull |
mob.arab |
1056 |
0.04 |
0.51 |
|
15 |
Northern Urals (Russia) |
jbb.pol |
337 |
0.36 |
0.31 |
|
36 |
Yamal (Russia) |
mob.yam |
266 |
-0.06 |
0.39 |
|
37 |
Taymir (Russia) |
mob.tay |
273 |
0.28 |
0.2 |
|
41 |
China: composite (degC) |
mob.yang |
849 |
-0.52 |
0.7 |
|
40 |
Shihua Cave: layer thickness (degC) (China) |
mob.shih |
708 |
0.24 |
0.44 |
Before providing a commentary, I will show what Juckes presents as a statistical model, though it would hardly pass muster as such in any journal with adequate statistical refereeing. In his Appendix, Juckes hypothesizes that there is some sort of “noise” process that generates the proxies as follows, first, saying for the inverse regression case:
Now the model for proxies in the VZ pseudoproxies is an admixture of white noise to gridcell temperature. It’s obvious that the above residuals are not generated by a white noise process or for that matter a low-order red noise process. It seems quite possible that at least some of the proxies may be completely mis-specified and have no relationship to temperature.
The problem with the residuals is particularly apparent with the Arabian Sea G. Bulloides series and the Yang composite (incorporating a highly smoothed version of Thompson’s Dunde ice cores). The residuals for the two foxtail series – Upper Wright and Boreal – are also very problematic, as are the residuals for the Yamal substitution.
Thus, we have the curious situation where the series that have been identified on many occasion at this blog as being problematic – foxtails, Yamal substitution, Arabian Sea coldwater diatoms (G Bulloides) and the Dunde ice core (Yang composite) – recur yet one more time in one of these little data-snooped exercises, with, as usual, residuals in the red zone.
It is also remarkable just how low the correlations of the snooped data sets are with gridcell temperature. The two foxtail versions have slightly negative correlations to gridcell temperature – a result which is also consistent with Christy’s recent calculation of a high-elevation Sierra Nevada temperature history. Osborn and Briffa reported a correlation of 0.19, but, when pressed, it turned out that they had not used HadCRU2 data between 1870-1888 because the temperature data was “flawed”. The Yamal substitution has a slight negative correlation to gridcell temperature, although on a very limited record. The strong trend in Arabian Sea G. Bulloides percentage is not reflected in gridcell temperatures. (As noted on many occasions, these are subpolar foraminifera and in Gulf of Mexico cores, their percentages increase as one goes back to the last ice age. It was originally developed as a proxy for monsoon wind strength, Its use in this context is not based on it being a demonstrated temperature proxy, but on opportunism, originally in the Moberg study). The Yang composite uses a very obsolete version of the Thompson Dunde ice core series; if the Yang composite is re-compiled without the Thompson series, it has a very different look.
There are many interesting aspects to each of these 18 series. I could probably do a separate post on each individual series and may return to this on another occasion.
For now, just from inspecting graphs of the residuals, I do not believe that it is possible to define a “noise” process from which these particular proxy series can be said to be “independent” realizations. If there is, then it would have to have very exotic qualities to yield each of the above residual series as “independent” realizations. Obviously Juckes has merely asserted that there is such a process 
Climate Audit 
35 Comments
I can’t imagine how you could get a hockey stick out of that data set.
I can’t imagine how much you would have to sacrifice your ethics to come up with a hockey stick from that data set.
Some of the proxies seem to have higher correlation with temperatures than the others. Why wouldn’t an ethical scientist discard the data that has a low correlation (or negative correlation) and build a model based on the higher correlated data only?
The first four plots, left column, look to have identical CRU gridcell data. The proxies, however, track the temperature differently. ecs.upp and ecs.bor start below and end above the CRU data, and in fact almost look like the same proxy series differently processed. It’s clear, however, that neither the negative excursion around 1860 nor the positive excursion near 1980 in these two series can be justified by reference to the CRU data.
Even where they look to approximately track the CRU data, a close look shows the proxy jitter to often be out of phase from the CRU data. It doesn’t look like there is an annual lag-1 in the proxy response, either, though I haven’t the data to plot so as to know for sure. With respect to out-of-phase jitter, the same is true of the two mob proxy responses as well.
Is it peculiar that the two mob proxies have a family resemblance (slope approximately zero) and the two ecs proxies likewise (slope approximately positive), but the two sets don’t look like one another, despite apparently reflecting the very same temperatures? Doesn’t this variation against the same temperature field advise caution in using proxies at all to reconstruct temperatures?
mob.yang and mob.arab seem to show an inverse divergence problem. The temperature is stable or decreasing but the proxy ascends. Casting an eye over all the series, a few decline modestly in the late 20th century: mbh.morc, mob.tay, mob.ig, and mob.mw, and several modestly increase: esc.upp, esc.bor, mbh.queo2, and jbb.tor. An average of these look to conveniently yield a pretty flat 20th century. But then we have mob.yang, mob.arab, and mob.grip, which uniformly ascend after 1940. Toss these into the prior sum and it’s AGW-city.
Looking at the residuals, there *certainly* is not an “independent noise process” in evidence. Some of the residuals look distinctly periodic, such as ecs.bor, ecs.tor, and jbb.tor; mob.arab and mob.yang are ludicrous, and none of the residuals look at all like white noise, to my eye. Offhand, one may suspect the relevance of the statistical model.
Yes, and the expert dendroclimatologists will tell you they use caution. I guess it’s up to higher authorities to decide if that’s true or not.
All these proxies are junk, as far as temperature concerned. If you take out the one that have the same grid cell but chart differently on the grounds of inconsistency, those that don’t correlate with local temperatures, those that have a different correlation with local and NH temps, those that don’t have any local temp record at all, there is nothimg left.
Of the ones that have a high correlation to NH Temps, mob.grip, mob.arab, and mob.yang it seems obvious why they’ve been included.
They are the only ones that exhibit a marked rising trend. I expect the rest of the proxies are there only to provide cover. The three rising trend ones are needed to defend against charges of non robustness, ie you can now take out any two proxies and still get a Hockey Stick, and the mob.yang is cherry picked obselete data, arabian sea bulloides not a proxy for temperature. That leaves mob.grip, don’t know anything about that one, but it’s all on its own, and is actually recently exhibiting a falling trend.
All the staistical sleight of hand from the Hockey Team and Juckes is just window dressing to try and obscure the fact that their analysis is complete and utter nonsence.
I was mulling over things that could be a Juckes-noise process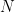
. It’s actually completely general. For example, under Juckes definition of a noise process 
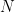, you could say that any series of numbers were signal plus noise – so you could make a network of stock prices, traffic flow at New York City bridges on an hourly basis, minute-by-minute trading volumes at the NYSE – make a network and say that these are all temperature proxies for 1400-1980 plus noise. Obviously there’s some sense in which we feel that modern stock prices are not proxies for historical temperatures. This would show up in the properties of the residual series between stock prices and historical temperature, which would not be white noise. In order to define his model, Juckes has to make a testable hypothesis about the signal-noise properties of this network – rising above the tautology of Juckes process 
.
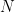Just thinking out loud, it seems to me that it’s fairly easy to conceive of unorthodox noise processes that would be a Juckes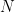
process, but which would not necessarily permit the application of CVM. Suppose that your noise “process” had a 90% chance of being white noise and a 10% chance of being a random walk or very high order red noise (AR1>.98). Try to prove that CVM is an “optimal” estimator. I don’t think that you can. Indeed, it seems to me that CVM would yield a radically biased estimate under such circumstances. I’m not sure how you’d prove it mathematically, but surely the optimal estimator is to exclude or radically downweight the series that have random walk noise. There would be all kinds of other possibilities – suppose that some noise processes are long-tailed dependent processes; while others are white noise. If the noise is all i.i.d. normal i.e. Rasmus-world, then you can assert optimality.
I don’t think that for Juckes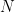
process without further restrictions, that one can claim that CVM necessarily has any meaning or claim to optimality. To do that, I suspect that you’d have to make restructions on the noise process – which would likely not apply here. Proving statistical theorems isn’t very easy and requires a lot more math than evidenced in Juckes’ Appendix; Juckes provided no citations to any statistical authorities to support his claims for a wildly general 
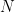process.
All my favourite proofs are listed here. The appendix appears to be proof by omission.
For a real proof – try this one.
“No, a proof is a proof. What kind of a proof? It’s a proof. A proof is a proof, and when you have a good proof, it’s because it’s proven.”
#5 Here’s a wild guess.
To get the 99.98% from the data available by normal methods is obviously impossible.
Therefor Juckes has in some way to reweight the data, giving the upswing proxies prominence.
His estimate of “noise” may well be simply the difference between the proxy temperature data, and the recorded temperature data. He then applies the difference in some way to the underlying proxies to somehow reweight the proxies. He could mess with the method enough to get to a 99.98% I’m sure. There must be a way to work back from the 99.98% using different variables for N noise to reach back to the proxy data.
Dr Juckes???
Are these correlations based on annual temperatures? At least some tree ring series have far higher correlation with growing season temperatures.
Re top: The bit McIntyre is mis-quoting from the appendix refers to the noise of the composite, not the noise of the proxies.
Re 1: Our reconstruction is a straigt average, after normalising the proxies to unit standard deviation. I’m not sure if you would call it a “hockey stick” though. I’ll leave that for the terminological experts on this site to clear up.
Re local correlations: we don’t assume local signal to noise greater than unity, and so lack of local signal to noise greater than unity does not invalidate our assumption.
Re selecting proxies based on correlations: the choice of technique is discussed in the manuscript.
WTF!??! From Steve’s quote above
And now you claim that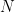
is noise of the composite!?! C’mon, you are not fooling anyone.
Steve/John A: Please, could you copy here my long answer to Martin (from “Juckes and 99.98% Significance”) as it is not currently showing.
Choosing proxies based on high correlation with the full range of observed temperatures is wrong. We need out of sample verification of models, and some data need to be set aside to do that.
Without an a priori theory of why certain data are good predictors of temperature, observed correlations today do not tell us anything about the relationship between temperatures and such series 1000 years ago. If I have a good theory of why a certain series should be able to predict temperatures, I would be inclined to keep it in the mix even if observed correlation with temperatures is not great.
Before one goes to historical data, there has to be a decent theory of why certain series are supposed to be good predictors of temperature, then experimental verification of temperature with a clear explanation of the relationship (whether it is linear or nonlinear etc).
Then, and only then, can one attempt to use historical data to say something about the future. Remember that, in a regression, the explanatory variables are assumed to be exogenous, coming out of a randomized experiment. When dealing with historical data, one has to take into account the fact that there can only be one observed history and it is not the realization of a randomized experiment.
In econometrics, we go to great lengths to take into account the violation of this exogeneity assumption. The same endoegeneity issue exists in historical climate data.
Statistical models based on historical data have to be evaluated on the basis of their out-of-sample predictive power. An easy way to do this is to use the historical data up to 1980 to estimate an equation for temperature. Then, these estimated relationships ought to be tested in predictive power using data from 1980 – present.
If out-of-sample predictive behavior is good, then we might have some confidence in longer term predictive power of proxies.
I don’t know who said it, but the following quotation was in one of my econometrics textbooks:
Sometimes the road behind you looks exactly like the road ahead of you, and, sometimes, you miss that sharp turn right ahead of a cliff. Ooops.
I would have hoped that there would be a few bucks spent on bringing the proxies up to date, but that is a whole different topic.
re #12/Steve/John A: It might be also under “Juckes and the Pea under the Thimble (#1)” I mean the one I wrote after Dr. Juckes confused me with Steve…
Jean S, I don’t know how to access the database. I’m going to arrange for an upgrade of the service package and that should recover the posts that aren’t showing.
How can this be a “misquote” – it is a physical image taken from Juckes’ article, not a comma has been re-typed.
#13 — Sinan Unur wrote: “Without an a priori theory of why certain data are good predictors of temperature, observed correlations today do not tell us anything about the relationship between temperatures and such series 1000 years ago.”
Sinan, without an a priori theory of why certain proxies are good predictors of temperature, one cannot tell anything about the relationship between temperatures and series today. The modern correlations may not be different from coincidental tracking. Without a theory, how would anyone know?
Looking at the graphics of proxies vs. temperatures posted by Steve M., the ‘sometimes yes’ and ‘sometimes no’ coincidence of proxies with CRU temperatures is more consistent with accidental associations than with some underlying deterministic commonality. The non-correlations of the jitters — which are not noise but rather the annual excursions of temperature and proxy behavior, respectively — are also consistent with this view and are a truly cautionary indication that the proxies are not following temperature.
Re: #17
Pat, it was not my intent to suggest that high correlations today imply causation today. What I was trying to point out, and you seem to agree with that, was that selecting proxies based on high observed correlations today is not appropriate without an a priori theory. The focus of my comment was on reconstructing the past, but it applies equally well to predicting the future as well. This was partially a reaction to #1: It does not make sense to focus on correlations without any theory. r = 0.1 with a good theory is better than r = 0.8 with no theory.
Anyway, I think we agree that these reconstruction exercises are futile for many reasons, not the least of which is that they treat any correlation as causation.
Sinan, thanks for the post where you say
There is a more fundamental reason. The average correlation of the proxies with gridcell temperatures is 0.10 ± 0.12 (95%CI). Thus, we cannot reject the null hypothesis that correlation = 0.
In other words, the proxies on average do no better than chance at recording local temperatures, so we don’t even have any correlation to treat as causation.
Here’s another oddity. For the four! proxies in gridcell 733, there is a strong inverse relation (r^2=.85, p = 0.03) between correlation with the gridcell and correlation with the NH. In other words, the better they represent the local temperature, the worse they represent the NH temperature. Another example of plantelepathy, I guess …
w.
#18 — Sinan, you’re right, we’re in agreement.
And #19, thanks again for a fundamentals-revealing analysis, Willis. You never fail. Your analyses are always so straightforward, and usually so damning, that we’re left with the truly basic question, which is: How is it that the researchers themselves didn’t discover (never seem to discover) what you can apparently find by taking a straight at’em approach to the data?
Come to think of it, within the context of statistical mathematics, Steve M.’s approach to proxies seems to be mostly straight at’em, too, and somehow the researchers also missed his findings.
This consistent evidence leads me to wonder: Does working in empirical climatology injure one’s foveae? Maybe OSHA should be appraised of this possibility, and issue a cautionary circular.
Well, I got to thinking about the correlations of the proxies with NH temperatures, and I thought I should take a look at the correlation of the gridcell temps with the NH temps. Here they are:
Figure 1. Correlation, gridcell temperatures with NH temperature, Jan-Dec:
Hmmm. Then I thought, well, the majority of the proxies are tree rings, I should look at the correlation during the growing season:
Figure 2. Correlation, gridcell temperatures with NH temperature, Apr-Sep:
As usual, curiosities. There are only a few gridcells in the NH that correlate well with temperature, either negatively or positively, and none of them are where the proxies are located. This makes any large correlation between a given proxy and the NH temperature suspect, particularly given the generally poor correlation between the proxies and the gridcell temps (no better than chance).
Also, I was surprised to find that the correlation of the growing season gridcell vs NH is in general less than the correlation for the whole year.
Always more to learn …
w.
I guess the reason that Juckes is so insistent that trees are not “thermometers” is because he thinks that they are radio receivers. Not just radio receivers, but ones that “integrate” northern hemisphere temperature.
I just did a Durbin-Watson statistic on the regression between the Juckes index and instrumental temperature. Dw statistic of 1.09 (!?!). Can you imagine a submission to an econometrics journal culminating in a univariate regression yielding a DW of 1.09 – especially one involving the econometric equivalent of individual trees “integrating” world temperature. I’ll do a post on this renewing the link to Granger and Newbold 1974 on spurious regression.
Willis,
How do the grid cell temperatures of the proxies selected correspond to the NH temperatues in the calibration period?
Re #21
Willis,
I don’t think there is anything wrong with those correlations you show. All it shows is an approximate ratio between global and local temperature variations in each of the grid-cells. What is important is that there are consistent positive correlations across the globe. You will not get a uniformly strong correlation unless there was no local temperature variation. Consider the extreme – for everything to have a perfect correlation with global temperature, every grid cell would have to be identical.
Alternatively, consider 2 gridcells and then an average of the two. What will be the correlation of the average with each individual gridcell? It won’t be ‘high’. Now, consider the case for larger numbers of gridcells. Indeed, given the number of gridcells, I think your correlations are probably suggestive of there being a common component to gridcell temperature because the correlations are higher than you would get with each gridcell being uncorrelated with all the others and the ‘global’ temperature being an average of those.
re: #24 John S,
You might have a point… If it weren’t that the proxies were cherry picked (or data snooped) to begin with.
Cherry picking is a problem no doubt. But I don’t think it affects my comments about the correlation of grid-cells with global temperatures. It should be small and positive. Proxies, on the other hand, should have a strong correlation with local temperature. Because otherwise it violates the hypothesis – that they respond to (local) temperature – that supports their use as proxies in the first place.
Re:#24
Umm, isn’t it that temps would have to *vary* identically, not *be* identical, for perfect correlation? Thus, there could be plenty of local temperature variation, as long as the pattern of that variation was fixed.
Yes – my bad. Identical up to an affine transformation (just threw that term in for the hell of it).
Re #20
I suspect they never read Feynman as students. Whereas I did.
Re #21
Those correlations are awful. Mind you, the scale of interpolation (or kriging) of the correlation surface matters. A global extent map with large-ish grid cells might smooth over otherwise locally highly significant correlations at specific places (e.g. White Mts, etc). [But I wouldn’t hold my breath.]
Where the correlations are exceedingly high, Willis, (e.g. equatorial Atlantic) is this because of a shared trend resulting form exceeeingly high autocorrelation? i.e. Perhaps the correlations are non-significant when you adjust them using Quenouille’s method? (A demo of Quenouille’s effect would be instructive.)
Bender, an interesting question above. I don’t know the answer in general, but the Atlantic correlation is significant.
w.
🙂
I hear empire down…
At what point do the climatologists (e.g. IPCC reviews) go from statements that suggest the lack of correlations between proxy response and temperatures merely increases the uncertainty of the results to something at least strongly indicating that that lack of correlation is a non-starter for the entire reconstruction process and that the Mannian and progeny reconstructions, while instructive in the limitations of the methods employed and the difficulty in finding valid proxies, point to the need for entirely new approaches with better methodology, based on a priori assumptions and with more detailed physical explanations for proxy responses to temperatures.
One can certainly see those climatologists, who have convinced themselves in others ways that we could be into a tipping point of climate change with no return, being in a “hurry” to make their points about AGW and self proclaiming that the “right” reconstructions can be very influential in climate policy decisions. When the reconstructions using proxies are shown to be very difficult and need significantly more time and effort to make valid cases, the natural tendency is to attempt to fix the past reconstruction on the run and, once again, in a “hurry”.
My viewpoint is that of an interested layperson and perhaps I am missing some of the nuances of the involved statistics, but I have less doubt the more deeply I look into these issues. Much of the criticisms of the reconstructions cannot be answered directly and tends to lead to answers such as the particular criticism may be correct but so what and without the scientist being questioned seemingly feeling the need to reply directly. A general tactic, at least as it plays out, whether intentional or not, would seem to be to get into another slight variation of the initial approach, as in “moving on”, and reporting the results as some new and independent approach.
I do need to finish reading the Union paper in its entirety, but I have read the paper’s review of past reconstructions and the criticism of those reconstructions. I find the paper tends to either overlook or fail to deal with the basic weaknesses of the reconstructions and so ends up giving a rather superficial view of the processes and criticisms of them.
The paper does point to apparent inherent problem with inverse regression in reconstructions measuring the full range of past temperature variations e.g. Mann et al. (1999). They then point to a paper by Mann et al. that tends to refute this and leave it as an open issue. They apparently have moved on to CVM but in my view without reasonable a priori justifications for the proxy selections and without (at least to my point of reading) a reasonable explanation for the lack of correlation of proxy response to local grid cell temperatures.
They also pointed to the Burger et al. paper showing the wide array of reconstructions that can be derived using the same pseudo-proxy data, but fail to reply to it and instead make a case that the another Burger point that increases in uncertainty of temperature estimates occur when going outside the calibration temperature range do not apply since one can assume that the calibration temperatures cover the entire reconstruction range.
Since, because of my participation at the CA blog, I feel more confident in my understanding the MM published criticisms of Mann et al., it is apparent to me that the Union paper’s remarks on that criticism are indirect and off the mark.
I think the course that has apparently been taken by the majority of climatologists will slowly crumble away the problems involved with climate reconstructions and at a rate related to policy requirements and eventually political demands for truly justifying policies that might be put into place that require immediate adverse consequences for the voters.
“…since one can assume that the calibration temperatures cover the entire reconstruction range.”
A perfect example of proof by assumption:
Assume that the range of temperatures does not exceed that of the instrumental (calibration) period. Therefore, the range of temperatures does not exceed that of the instrumental (calibration) period.
#11 Dr Juckes as
Did you produce a graph without mob.grip, mob.arab, and mob.yang ?
This would help emphasise the robustness of your paper.