Wahl and Ammann 2006 reported that they could “get” something that was sort of HS-ish without principal component analysis. It wasn’t through a simple mean or CVM; it was through Mannian inverse regression. Juckes et al shows many reconstructions using “inverse regression”, mentioning in his conclusions that inverse regression caused over-concentration on a few proxies.
we have found that inverse regression tends to give large weighting to a small number of proxies and that the relatively simple approach of compositing all the series and using variance matching to calibrate the result gives more robust estimates.
This is not the only potential problem with inverse regression in this type of network. Here’s a diagram which I showed in my European trip to Juckes co-author Nanne Weber at KNMI. In the top left corner (magenta), I’ve shown a Mannian reconstruction using the 68 non-stripbark series in the AD1400 network; the two black series show Mannian reconstructions using AR1=0.2 red noise; the red series is the CVM of the 68 non-stripbark series. Visually the reconstruction using non-stripbark proxies is very similar to the reconstruction from the same method using red noise. Both methods give quite decent correlations in the 1902-1980 calibration period. Note that the Mannian regression method flips over the reconstruction using the average of the series.
Consider what this means for Mannian calculations in which confidence intervals are estimated using calibration period residuals. Yes, the Mannian calculation yields a standard error, but the standard error is not measurably lower in this case than the standard error from red noise. Also there is obviously not a HS without the stripbark samples.
Top left — WA variation on 68 non-strip-bark series; black — WA variation AR1=0.2 red noise simulations; red- average of non-strip-bark network
In another post, I’ll show what happens when you add in HS-shaped series. For now, I just wanted to illustrate in another format the meaninglessness of the Wahl and Ammann fit.
While the fit is meaningless, I think that there is a decent possibliity that the Wahl and Ammann no-PC regression could become a statistical classic as one of the most remarkable examples of overfitting that I’ve encountered.
Climate Audit 
11 Comments
Inverse regression? What? Regression is signless, unless, oh silly me, it’s ordained to be inverse when we stand on our heads and do the regression computation.
Geee, modern education is very progressive, isn’t it.
#1: A decent M.Sc. thesis on the subject:
Click to access thonnard2006.pdf
I’m quite sure that there are papers on this topic somewhere (overfitting / overprediction in calibration problems). For univariate case, Brown (1) gives a confidence region which is
and
I’m sure this applies to multivariate case as well, i.e. 1) in calibration make sure a priori that there is a (linear) physical relationship between x and y 2) Don’t use calibration residuals for evaluating the model.
1) P.J. Brown (1982) Multivariate Calibration. Journal of the Royal Statistical Society. Series B, Vol. 44, No.3. pp 287-321
Is there any generally accepted approach to avoid the problems introduced by “inverse regression”? If the proxies (denoted Prox) are each functionally dependent on temperature (denoted Temp), then the correct functional relationship is something like Prox = Temp + error. If we then try to use that model to predict Temp from Prox (rather than Prox from Temp; there’s a switch here), we are no longer in the world of linear regression. It may look a lot like linear regression to the non-statistician; but it isn’t linear regression.
Kendall and Stuart (Chap 29, “Advanced Theory of Statistics,” vol 2, 4th ed.) devotes a whole chapter to this problem (“functional and structural relationship”). My reading is that things are a mess, particularly if one recognizes the existence of measurement error in both X and Y variables.
The problems vanish if all the error variances are sufficiently small. But I’m not sure that’s the case when dealing with climate reconstructions.
#4. The term “inverse regression” has to be used cautiously. “Inverse regression” has a meaning in statistics, which is different than Partial Least Squares regression.
In circumstances where the proxies have considerable orthogonality – if one can talk this way – Partial Least Squares regression approaches Ordinary Least Squares regression. OLS rotates the PLS-coefficients in n-space by the matrix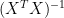
. The proxies in (say) the MBH98 network are surprisingly orthogonal. Mixing Partial Least Squares regression with prior processing using Principal Components is not an obviously consistent procedure – the prior Principal Components operation generates orthogonal series, which are exactly what you “shouldn’t” want for Partial Least Squares regression.
In the case of the MBH98 network (and I suspect that it’s also true for the MBH99 network), the PLS regression coefficients are surprisingly close to OLS coefficients.
#4
There is also a section on Calibration (32.76-32.77), (6th edition)
For the multivariate calibration case, the reader is referred to Brown 1982 (the same as in #3) .
Hi Steve!
Do you read the new Wahl-Ammann paper in Climate Change “on-line first”?
From abstract:
«Altogether new reconstructions over 14001980 are developed in both the indirect and direct analyses, which demonstrate that the Mann et al. reconstruction is robust against the proxy-based criticisms addressed.»
Excuse me if I’ve resumed this ancient post!
#7. Yeah, I’ve read it. They’ve had to do some jerry-rigging to deal with rejection of Ammann and Wahl (GRL). They’ve replaced these references with citations of Ammann and Wahl 2007 – Climatic Change, accepted in June 2007, which went online recently (as was noticed here.) It’s interesting that a paper which was supposedly “in press” by February 2006 to meet IPCC deadlines relies on a paper accepted only in June 2007.
I previously commented that Wahl and Ammann had been engaged in “academic check kiting”. In this case, they seem to have realized the absurdity of citing a rejected paper and tried to cooper up the situation. From my perspective – and I’m used to business situations, I would have said that any “acceptance” of Wahl and Ammann 2007 must surely have been conditional on the rejected companion article being accepted somewhere and that it is false to say that it was “accepted” on March 1, 2006. (This matters only because they were already being cute with IPCC publications deadline.) IPCC “needed” this article because otherwise there was no journal article that could be used to argue against our criticisms.
Their emulation of MBH exactly matches ours, as I observed in May 2005 and most of our results, given the same assumptions, are virtually the same.
I;ve reported a lot on this – see http://www.climateaudit.org/?cat=20 . Not much has changed here.
As I reported earlier, in late 2005, I suggested to Ammann that, rather than engaging in further controversy, we try to write a joint paper summarizing what we agreed on. Ammann said that it would be bad for his career advancement and thus the controversy continues. On an earlier occasion in June 2005, they tried to trick Stephen Schneider about the rejection of the GRL article. They only included the failed verification r2 statistics after I filed an academic misconduct complaint.
I guess that I’ll have to bestir myself to respond to this dreck formally. Ammann and Wahl make so many misrepresentations of the issues that it’s hard to write a journal response without being tedious and yet there are a lot of spitballs that need to be picked off the wall.
The submission and acceptance dates of the articles.
Did I understand this correctly, they replace original MBH98 proxy data (with PCs) by a larger set of proxy data (no PCs).
Then, data is run through MBH98 machine, and not much differences are found, except that offset in verification mean rises 0.1 degrees.
If so, nice result, but degrees of freedom should be taken into account. As in Brown’s multivariate calibration confidence formula,
which takes this kind of overfitting (large amount of responses) into account in the uncertainties.
Thanks Steve!
I’m an italian archaeologist, not a climate scientist, but (or just for this!) find egually absurd the “Mann’s hockey stick”.
These continuous attempt to discredit your study reveals the irritation that you have caused!
For the climate science is important the consensus, not the facts!
For the non-statistician, Wikipedia has a nice discussion of the perils of [http://en.wikipedia.org/wiki/Overfitting Overfitting] — “An absurd and false model may fit perfectly if the model has enough complexity by comparison to the amount of data available.”
If someone here has access to the Encyclopedia of Statistical Sciences , they could post their definition of Inverse Regression here.
Also see the new http://climateaudit101.wikispot.org/Glossary_of_Climatology_Terms — a work-in-progress.
Cheers — Pete Tillman
ClimateAudit 101 team
http://climateaudit101.wikispot.org
One Trackback
[…] be even more embarrassing to the climate science trade than MBH98 ( see posts here , especially here here here […]