Many of the good folks who write the papers and keep the databases seem not to use their naked eyeballs. By that I mean, they seriously think that you can invent some new procedure, and then apply it across the board to transform a group of a thousand datasets without looking at each and every dataset to see what effect it might have. Or alternatively, they simply grab a great whacking heap of proxies and toss them into their latest statistical meat grinder. They take a hard look at what comes out of the grinder … but they seem not to have applied the naked eyeball to the proxies going into the grinder.
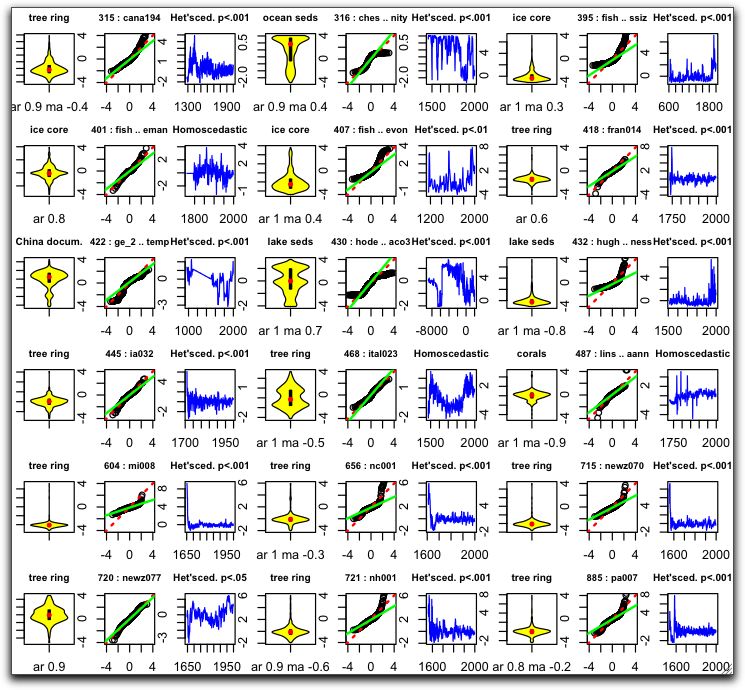
So, I thought I might remedy that shortcoming for the proxies used in Mann 2008. As a first cut at understanding the proxies, I use a three-pronged approach — I examine a violinplot, a “q-q” plot, and a conventional plot (amplitude vs. time) of each proxy. To start with, let’s see what some standard distributions look like. The charts below are in horizontal groups of three (violinplot, qq plot, and amp/time) with the name over the middle (qq) chart of each group of three.
A “violinplot” (left of each group of three, yellow) can be thought of as two smoothed histograms back-to-back. In addition, the small boxplot in the center of the violinplot shows interquartile range as a small black rectangle. The median of the dataset is shown by the red dot. Below each violinplot are the best estimates of the AR and MA variables as fit by the R function “arima(x,c(1,0,1))”. Note that in some cases either the MA coefficient, or both the AR and MA coefficients, are not significant and are not shown.
The “QQ Plot” (center of three, black circles) compares the actual distribution with the theoretical distribution. If the distribution is normal, the circles will run from corner to corner of the box. The green “QQLine” is drawn through the first and third quartile points. The red dotted line shows the Normal QQLine, and goes corner to corner. It is drawn underneath the QQLine, which sometimes hides it if the distribution is near-normal.
The standard plot (right of three, blue) shows the actual data versus time. The heteroscedasticity (Breusch-Godfrey test) is shown above the standard plot, with a rejection value of p less than .05.
Below are some possibile distributions that we might find. A number of them look related to “power law” type distributions (exponential, pareto, lognorm, gamma, fdist) although there are subtle differences. These all look like the letter “J”, and seem to differ in the upper tails, the tightness of the bend, and the placement of the QQLine.
The sinusoidal, Sin + Noise, and Uniform distributions all look like the letter “S”. Comparison with the QQLine shows that there is too much data in the tails. On the other hand, the “normal squared” distribution is a signed square of a normal distribution, and has too little data in the tails.
Finally, note that the ARMA distributions are not at first blush visually distinguishable from normal distributions. However, as you can see by the blue plots, they are more lifelike.
With that in hand, let’s take a look at some of the Mann proxies. What I did was simply go through the proxies and look for anomalies, proxies that seemed strange in some way. I didn’t look at numbers, that comes later.
I’m not sure what to say about the first 18 proxies shown below. A number of these (5, 15, 73, 249, 293) have a very high value in the first years. This gives them what appears to be a power law distribution … but looking at the standard plots in blue, it is obvious that they are not power law distributions. Instead, they are a normal-like distribution with something strange going on in the very first part of the record. Others, like 197 and 204, are known in the trade by the technical term “kinda goofy distributions”. And some, like 22, seem to be fine except for one year that’s way out of kilter. (As an aside, #22 is an excellent example of a proxy where the naked eyeball immediately identifies a problem which the statistics have trouble picking out.)
In the next set of 18 proxies below, we start wandering further afield. Does it seem reasonable that 422, 430, and 468 are temperature proxies? Did they really use the interpolated values in 422? What’s happening at the start of 418, 604, 656, 715, and 885? What’s going on with the recent data in 432? And 316 is just plain bizarro, asymmetrically bimodal with the median (red dot) way up near the top.
Below is a final set of 18 proxies, and the fun continues. To start with, at 897 it looks like we have a real live Poisson distribution, but it is apparently bounded at the top … what’s that doing here?. 899 looks like it might be some kind of binomial. 1017 looks like a true Pareto or power-law distribution. 1044 appears to be three different records laid end-to-end. 1055, one of Thomson’s mystery proxies, starts small and increases steadily for a thousand years … temperature proxy? You be the judge.
Moving on, 1062 is one of the proxies that is known to be compromised in recent years. We have more of the early-year high value problem in 1111 and 1148. On the other hand, 1176 is both high and low at the start. And I don’t have a clue what’s going on in the last three (1204, 1206, 1208), except that 1208 looks like an upside-down power law of some kind.

Now, I must confess, I don’t really know how to sum up Mann’s list of candidate proxies. I would call it an “undigested dog’s breakfast”, were it not for the implicit insult to the canine species. For some of these proxies, like 1148, we might be justified in chopping off the early years and using the rest. For others, rejection (or in some cases driving a stake through their hearts) seems more appropriate.
So let me pose a more general question. Mann is using his own special Pick Two comparison method to select, from among these 1209 starting contestants, the proxies that have some nominal relationship with recent temperatures. But it appears to me that the process badly needs some kind of “pre-selection” ex ante criteria. These criteria would weed out those proxies which, although they might pass the “Pick Two” test, and they assuredly pass the “grab any proxy” test, don’t pass the naked eyeball test. But the naked eyeball test is not mathematical enough for the purpose. My general question is:
What kind of ex-ante test might we use to exclude certain categories of these proxies?
As a first cut at this question, it does seem that if a proxy is sufficiently heteroscedastic, it should be excluded. One of the main ideas of reconstructions using proxies is the “Uniformitarian Principle”. This principle states that physical and biological processes that connect environmental processes to the proxy records operated the same in the past as they do in the present. This Uniformitarian assumption underlies all proxy reconstructions. We assume that the same physical and chemical rules that connect temperature and proxy in the period of the instrumental record have applied throughout the history of the proxy. And as such, the record should reflect that unvarying influence by having relatively constant variance over the period of record.
In addition, regardless of the Uniformitarian Principle, we need to use proxies that are at least somewhat stationary with respect to variance, or our statistics will mislead us. If the proxy variance is different in the present and the past, we will under- or over-estimate past temperature variance.
Looking at the records above, I would suggest that any proxy record which is heteroscedastic at p less than 0.01 should be excluded from consideration. This would not rule out all of the … mmm … “more interesting” records above, so it might be a “necessary but not sufficient” test for candidate proxies. However, it does distinguish between 107, which I had called a “true Pareto” before checking the scedasticity, and 1062, a known bad proxy.
Finally, I did not choose the proxies above by any statistical methods. I just picked these because they struck my eye. And there are plenty more. I had to whittle my choices down a ways to get to the 54 proxies shown above.
And as I found out after making these selections, of the 1209 proxies, no less than 571 of them are heteroscedastic at p less than .01.
CONCLUSIONS
1. I picked these proxies out, not by looking at their homoscedasticity, not by any kind of statistical analysis, but simply by looking at each and every one of the 1209 Mann proxies. The human eye is a marvelous tool.
2. This process can be described by one word … boring. It is not as glamorous as flying to England to help free vandals, or as interesting as testifying before the US Congress about how you are being muzzled.
3. Nevertheless, it is the most crucial part of the process. Why? Because it is the part of the process that only a human can do. Only by examining them, proxy by proxy, can we come to any reasonable conclusions about their possible fitness as temperature proxies.
Best to everyone,
w.






43 Comments
Isn’t that what statisticians call stationarity?
Nice one Willis. As usual, a picture is worth a thousand words.
John A, you ask a good question:
My understanding is that “stationary” in statistics is a bit different. It does not concern itself with the connection of two physical process (e.g., tree rings and temperature). Let me see what I can find:
OK, I find: STATIONARY: a process where all of its statistical properties do not vary with time.
This differs from the Uniformitarian Principle, in that stationarity is a property of a dataset, whether it is randomly generated or represents a physical process.
Regards,
w.
The naked eyeball approach should be sufficient if justification is provided.
What does your reconstruction of the temperature history look like given the 571 proxies that meet your eyeball test?
It’s a bit sad that someone would need to counter #422 or 316 with math.
I propose a giggle test. If you put the curve in front of a class of fifth grade students and 90% see a problem the proxy is out.
I still haven’t figured out how people think this might be in any way related to temp.
Very nice post.
claytonb and Jeff Id, while the “eyeball test” and the “giggle test” are good, they are also susceptible to cherry picking. To avoid that, we need to set up ex ante mathematical standards that can unequivocally rule a proxy either in or out. That way, we can dispute about what the standards should be, but once they are agreed upon, we can rule proxies in or out without favor, prejudice, or cherry picking.
Xavier, once we can actually figure out what Mann has actually done (which is generally != to what he says he has done) we might be able to answer your question …
w.
From my recent work on back calculating the mann08 graph I think you may be right about Mann’s latest paper not being exactly what he said.
I could be wrong but watching the series converge for hours with different methods left me to believe that certain proxies weren’t correct or something was missing.
As far as sorting data, I think that the old fashion method of — if a proxy is measured the same way as the rest and no obvious collection flaws are found you keep it. If the total set of like extracted data doesn’t match temp it likely isn’t. The whole concept paleoclimatology uses of throwing out data which doesn’t correlate is really over the top.
Still, your suggestion of eliminating heteroscedastic data seems credible. I like it because it is a quick sanity check before looking for correlation trends. But why would we keep any of the other mollusk shells, tree rings or historical documents if some of the related series cross the threshold of credibility? To me if one data set of like collected proxies is scrapped, we have to very carefully question the rest from the same group.
Also, we can’t forget that 90% of these 1209 proxies have high correlation data pasted on the ends using RegEM glue.
Jeff Id, you raise an interesting point:
This strikes me as getting close to “guilt by association”, a type of false accusation that has been made against many climate scientists who don’t believe in AGW.
So while a bad proxy could certainly mean we need to “question the rest from the same group”, the fact that some particular proxy is bad could arise from a variety of sources. It might be that the proxy and all of its cousins is inherently bad. Or it may be a result of bad sampling. Or, as in the case of the lake sediments, human influence may make recent years in a particular lake sediment proxy untrustworthy … but should we mistrust all lake sediments on that basis?
What I have learned from Steve M. is to take small, patient steps, and to avoid large, overarching conclusions. My intention is to leave the giant steps, and the “new statistical methods”, and the unsustainable conclusions to the AGW believers. The fact that Mann does worthless things with proxies does not imply that proxies are worthless. The fact that one proxy is rubbish does not mean all proxies of that type are rubbish. Those are steps too far …
All the best,
w.
Perhaps if more than a certain % of proxies (in a group) fail a pre-defined sanity test, then the group as a whole should be considered highly suspect, and so thrown out?
This is where the physical meaning and attributes of the proxy data — and proxy sources — becomes crucial.
We’re talking about all this as if it were only a statistical exercise. In reality, these are all measurements of something physical.
Variations of this sort tell me the original measurement paradigms need significantly more study.
For example (obvious given my past 😉 ), if you get huge variations in tree ring samples, do you simply accept/reject based on ex ante statistical properties, or do you go back to square one and determine the meaning of outliers?
Outliers could be bad sampling, sure. They also could derive from any of a variety of physical anomalies that cause disqualifying variation for particular trees, or trees in a particular place, or trees that have experienced particular environmental impacts.
Bottom line: seems to me that the statistical tests are fine, but the action taken should be further analysis rather than assuming the data can/ought to be tossed.
Hi Steve, I may have something on tree rings for you with which you can do some original research. My garden hedge has about 40 Leylandii trees that were planted 19 years ago. All the trees are the same variety and were about 18 inches high when planted and all had pretty much the same trunk diameters when planted. They have been pruned each year to keep them the same height and width – it’s a hedge after all.
Now, there is a huge variation of trunk diameters. Some of the trunks are twice the diameter of others even though they have been sharing the same climate. Obviously the difference is to do with total growing conditions and genetic variability, but that’s the point. The width of the tree rings does not correspond to temperature.
If you want, I’ll measure the circumferences next weekend for you. It would be interesting to see some statistics analysis.
Re: Alan (#12),
I think that the phenomenon you comment is already taken into account when analizing tree rings. You don’t compare one tree to the next one, you only compare among rings from the same tree. Let’s put it this way. You have your tree A with twice as big a trunk as tree B, grown in the same period of time. You will choose one year to make comparisons, let’s say 10 years ago. You can call that your base temperature. For tree A, you will compare the rest of its rings to its “ring10” and see how hotter or colder the years were compared to year -10. For tree B, you will do the same, but now you compare to the “ring10” of tree B. After doing that with all trees, you average the results. The assumption that you make is that, yes, different trees grow at different rates, but a good year is a good year for all trees, and a bad year is a bad year for all trees. It is not a very good assumption but it is not as bad as what you said.
Excellent work.
Mann and cohorts have a Machiavelian Momentum operating in the funding, publishing, and popular reporting of climate science. One may quickly spot their errors and point them out–and it is critically important to do so–but their momentum has carried them on beyond one’s reach, in practical terms. You are asking them to scientifically justify the root basis of their work, when they have no overriding reason to do so, based upon of real science (realpolitik) as it plays out on the larger stage of funding, publication, and institutional pressures.
In retrospect, the rotten foundation will become clear, and I hope this blog receives a large share of the credit for exposing the dangerous weaknesses.
Mr Pete:
It sounds like you are saying that the proxy measure is a function of potentially a number of variables of which temperature may be one. In order to partial out the possible temperature record one needs to specify as many of the other variables as possible before one can say anything particularly definitive about the effectiveness of the measure as a temperature proxy. My read of Willis’ intriguing tour through the proxies is that he is sorting out those that might be “pure” temperature proxies. This leads numerous other proxies where we simply do not know which variables are important.
Willis, if your experiences with these supposed temperature proxies is any indication, it would appear there is justification for applying a Data Quality Objectives (DQO) philosophy to this effort, one which employs a Systems Engineering approach to integrating the data collection processes and the data analysis processes end-to-end, and which uses foundational knowledge and foundational prior research as a basis for designing and developing a tailored DQO process which can deal with the kinds of issues you are encountering. Does anyone know if such a DQO-like philosophy has been applied to Mann’s proxy analysis work, even if it hasn’t been specifically labeled a “Data Quality Objectives” type of approach?
#9 and #10
I didn’t mean throw away all sediment cores for one bad one. I think Chris H worded my thoughts better than I did.
I just did another post on data sorting and how it influences the final result. If we find a large percentage of data needs to be removed then we are no longer sorting for problems but rather for what we want to find. My simple post sorts like Mann did for the calibration range data. What’s amazing is what happens to the historic temperatures just by choosing the “best correlation” trends.
If you have two sediment cores by the same method and same people in the same area and a one is considered bad. Perhaps the bad one is actually the good one and we’re not looking at what we think.
So i guess I am saying, if there is enough statistical problems in the data of a type collected at a certain location individual problems can be compared to physical processes. As in verified pollution or other contamination to scrap a certain series. But as a whole all grouped proxies need to be verified or scrapped as a group rather than individually. Anything else biases the result.
If it is not done this way, we will trick ourselves with statistics into accepting data as temperature which is not. I.e. tree rings and paleoclimatology.
I would like to invite you to see my blog on statistical sorting.
I don’t know. It seems an eyeball test opens up a can of worms. It has to add a subjective element. Clearly differing proxies need to be evaluated and somehow gauged though.
I would be careful throwing away proxies because they are heteroscedastic or anything else. The data in hand may reflect a concatenation of effects and may not be a simple set of data like say river stage or rainfall at town X. For example, in an ocean sediment core, there are usually control points where the date is estimated by some method (sediment accumulation rates curve, or isotopes or whatever) and then the dates inbetween are estimated. This adds one type of error. Then, samples are taken and a laboratory procedure gives a number for some property, again with error. In contrast to tree rings where the dating and measurement error are small compared to the values, here the errors are not small and may not be iid or normal. On top of all this, is the weather generating the incoming signal which can have LTP or not, which could vary over time. Finally, there is the effect of the true long term trends in the data, which will impart some sort of distribution on the data. During the last glacial, the DO (Dansgaard-Oschger) events would give long cool periods with short warm periods interspersed, for an odd distribution of temperatures, not normal or lognormal or anything. The consequence of funny data distributions is that your correlations with recent temperature (your keep/toss test) will be all goofed up (that’s a technical term…).
First, my thanks to all who have replied.
Craig, thank you for replying. You say “I would be careful throwing away proxies because they are heteroscedastic or anything else. The data in hand may reflect a concatenation of effects and may not be a simple set of data like say river stage or rainfall at town X.”.
You are correct. However, my point was a bit different. It seems that Mann et al. have grabbed a whole host of proxies which have obvious problems. To take one example, we don’t know what caused the first decade or so of the first proxy above (#5) to be wildly larger than the following 250 years of data.
Nor do I particularly care. It might have been fire, flood, or famine, or the tree that shaded it died. It might be a transcription error … so what? The point is, I think we can all agree that it is obviously unsuitable as a temperature proxy.
My question was, what is the best way to mathematically weed out proxies like that one? I don’t think that the answer to that question is “be careful throwing out proxies”. Yes, I agree that we need to be careful throwing out proxies. However, I think we need to be more careful about letting proxies in. An occasional good proxy thrown out is not much of a problem. A bad proxy let in, on the other hand, could totally bias the results.
Mr. Pete, good to hear from you. You say “This is where the physical meaning and attributes of the proxy data — and proxy sources — becomes crucial.” While I agree with you 100% in a theoretical sense, the problem is that often the data necessary to make an informed judgment simply does not exist. So while we have reasonable grounds to suspect (for physical reasons) that tree rings might contain a temperature signal, to return to my example of proxy #5 above, this does not explain the high values in the early years.
Jeff Id, I appreciate your citation to your interesting post on statistics. However, regarding my question you say: “So i guess I am saying, if there is enough statistical problems in the data of a type collected at a certain location individual problems can be compared to physical processes. As in verified pollution or other contamination to scrap a certain series. But as a whole all grouped proxies need to be verified or scrapped as a group rather than individually. Anything else biases the result.”
I don’t understand that idea. Suppose I take five measurements of the length of an object, and I happen to write one of them down wrong. Let’s say my measurements are 17.3, 17.2, 17.5, 17.4, and 47.5.
Does that one transcription error mean I should throw away all of my measurements? That seems like too blunt a tool to be useful. For example, in this case it is obvious from examining the data what has happened. I have typed a “4” rather than a “1”, they are adjacent on the 10-key keypad I use for entering numbers.
If I am convinced it was a transcription error, I can correct it. If I am not convinced, I can throw it out. And to speak directly to your point, neither of those options “biases the result”. But I would rarely do what you suggest, and throw out the whole set of measurements.
Finally, it is not clear what you mean by “all grouped proxies”. Does that mean “all tree rings” or “all tree rings from a certain area” or “all tree rings collected by a certain investigator” or “all tree rings from this species” or “all tree rings from this stand”? One of the reasons I’m reluctant to throw out “grouped” proxies is that the boundaries of the “group” are not necessarily clear. Are all ice cores a group? Are the Thompson ice cores a group? Are all Norwegian lake sedimentation studies a “group”?
Scott Brim, you ask a good question, viz: “Does anyone know if such a DQO-like philosophy has been applied to Mann’s proxy analysis work, even if it hasn’t been specifically labeled a “Data Quality Objectives” type of approach?”. Good news and bad news on that one, my friend. The good news is that such a process is ongoing … and the bad news is … yer looking at it. Welcome to Climate Science, where the obvious is … not.
bernie, you say: “My read of Willis’ intriguing tour through the proxies is that he is sorting out those that might be “pure” temperature proxies.” This is not the case. All I am doing is using the old eyeball test to identify proxies that appear to have problems, and looking for mathematical tests that can do the same. Whether these are proxies for anything, much less “pure” proxies for anything, much less “pure” proxies for temperature, is an entirely different question. It is an important question, but I’m looking at a much earlier step in the process, that of getting rid of bad data.
Now, I’ve posed a “heteroskedasticity” test to do that … but I’m not all that happy with it. Again, it is a bit of a blunt tool. What other tests might we use? It strikes me that one possibility is to compare the statistics of the supposed causative variable (in this case temperature) with that of the response variable (tree rings, etc.). Mann does this by seeing if the two datasets have significant correlation … but I’m proposing something different. This would be that some other statistical measures of the two datasets (e.g. tree rings and temperature) are compared. These might be the ARMA coefficients, the normality, the homoskedasticity, or some other measure.
However, as always, the devil is in the details …
My best to you all,
w.
I would propose a test to see what type of data would result from various processes. First a known climate signal (sinusoidal, whatever), then add an age model with dating error at the control points, then add sample lab error (can be done in stages, of course, depicting after each error source). What do the data look like using your plots above?
What I am doing such a poor job explaining is that sorting and removing data for a specific problem can impart trends. If there is a large removal of data for reasons which cannot physically be explained the whole group of similar tests needs to be questioned.
By “group” would require some observational decision, i.e are half the tree ring proxies from this study rejected? If so what is the phsical problem with the rejection? If it can be explained by transposing entered values then you have a good reason to reject a single series but each event needs to be individually explained or we are sorting for what we want to find.
If there is no physical explanation and it just seems different we cannot use this as a criteria for rejection of large portions of data. If you find heteroskadisticy in a significant percentage of mollusk shell trends from a single study, and want to reject them while retaining others from the study, there needs to be a physical explanation for the rejection. Without the explanation I would make the case that mollusk shells are not related to temperature and are only being sorted by our expected result.
I also hate to disagree with your brilliant comments, which I have read now about 5 times. But I do believe that elimination of a series or a large portion of series based on a statistical analysis not only can bias the result but it is guaranteed to bias the result. We just don’t know how, and it leaves people like me trying to show why you can’t do it that way.
In the case of obviously hideous series like some you pointed out above, it should be easy to find the physical explanation and the problem is resolved.
Craig, you propose an interesting way of looking at the problem, a sort of inverse Monte Carlo method, viz:
The only difficulty that I see with this (which is not insurmountable, and is actually a benefit) is that it requires us to specify a model (or a potential model, or a suite of possible models) that spell out the connection(s) between the independent and the dependent variable. (It is worth noting that many of the modeling efforts by AGW supporters have the stick by the wrong end. They think the independent variable is the proxy and the dependent variable is the temperature. But I digress …)
All in all, a fascinating idea. Let me think some more about this one …
w.
Jeff Id, thank you for continuing the discussion. You say:
I agree that if we exclude (or include, for that matter) some particular proxy it will change the results (or as you say, it “can impart trends”). However, we are not interested in unchanging results. We are interested in correct results … so if excluding a proxy changes the results from incorrect to correct, why should we care if it changes the trends?
I also agree with you that if we find statistical reasons to question say 71% of the Graybill bristlecone data, we need to look at and question the whole of the Graybill bristlecone data. You then go on to say (inter alia):
To use the Graybill bristlecones again, we don’t have a physical explanation for why his chosen trees have a hockeystick at the ends … but we know that they do. So even without having such a physical explanation, and despite your statement above, I would throw out his hockeystick shaped data. Does that mean we have to throw out all his data? Depends on whether he made it up, or just cherry-picked it. If he just cherry picked a large dataset and ended up with a lot of hockeysticks, the rest is real data … should we use it? None of these questions are easy.
I would not throw out all tree ring data just because some of it is suspect, or compromised, or cherry picked, or whatever. Your point is well taken, however. The more that we can find out about any possible physical or other reasons for strange-looking candidate proxies, the better off we are, and the better decisions we will make regarding their eventual fate.
Finally, I’m sorry my writing wasn’t clear when I said:
By “biases the result” I did not mean “will give us a different result”. I meant “will give us a worse result”. If I correct a transcription error, the result gets better, not worse. If I throw out garbage data and only retain good data, the result (as you point out) will be different. However, I would not call it “biased”.
My overall point is simple. It is not sufficient to do as Mann does, to simply gather up a double armfull of proxies and see if any of them are correlated with temperature. We need some kind of clear, verifiable, non-subjective ex-ante criteria to weed out those proxies which should not even be considered for any one of several reasons. It is the selection and the definition of those ex-ante criteria that forms the question at hand.
In our particular case, since the proxies are to be used to do historical reconstruction, any difference in variance between the recent data and the older data will bias the reconstruction. It is for this reason, rather than any reason involving a theoretical or physical explanation for an anomalous dataset, that I proposed using heteroscedasticity as a criterion.
All the best,
w.
How useful is a record with a missing year? In my time series work, a missing entry isn’t going to mess up the entire regression. So you might have a ‘three sigma outlier’ rule or something to wipe out all the single-crazy-year data by fiat. For most of these proxies, I can think of a laundry list of plausible reasons for extreme outliers, so I’d personally have no problem setting a threshold and wiping out outliers sight unseen.
I mean, an animal melts a spot on the ice. Or material is deposited by a non-climactic event. A clump is disturbed. Plague of locusts. Ruptured Beaver dam deposits fertilizer. Whatever.
On another note, IIRC some of these “temperature proxies” were not designated as temperature proxies by the people gathering the source data. In particular, there seemed to be a couple that were specifically identified as primarily precipitation proxies. If we’re adding non-temperature proxies and trying to extract temperature trends, there’s probably a long list of unconsidered non-temperature data that extends back for a substantial period of time. Dutch sea level records, wheat harvest records, whatever.
So what’s the criteria for getting onto the list of proxies in the first place? Dr. Loehle’s “Every study that’s calibrated to temperature by the original authors” method makes a lot of sense. That works the craziness out of each individual potential proxy on a step-by-step basis.
Re: Alan S. Blue (#25), you bring up an excellent question. How much are we justified in removing a single outlier? And a related question or two … if we take it out, what do we replace it with? And, is “ending better than mending”, to misquote 1984, in other words, should we “fix” it, or just throw it out?
I’m pretty agnostic on this one, but I’m interested in other folks ideas.
w.
I have not followed the exact details of the Mannchinations to see why they’re so insistent on continuous series. But why would I want to fill the gap with made up information? Even statistically sane estimations? I’d fit what I’ve got. Scatter plots, not line plots. My experience is with pretty direct observational data by the boatload. A random missing (and not replaced by estimation) point or two wasn’t going to substantially affect my error bars. But the original bad data point might be sufficiently off kilter to sizably shift the fit, variances and residuals all in one point.
I can see where this might be an issue with weighting the individual proxies in the Mann fashion. But I’m less clear on why there’s so much infilling. Particularly if that means you’re infilling with a flat line. If a proxy has less data – then it has less data. It should be less strongly weighted on that basis alone.
How do we know that some tree ring series are not homoskedastic and normal by chance?
Moving from these temporal datasets (which are harder) to spatial datasets brings up the ready example of estimation of ore grades from spaced drill holes in an emerging ore deposit. The common aim is to get the data as close to correct as can be conceived, for an affordable cost. For mining, correct means that when the ore is dug up and extracted, it shows the same concentration as was estimated from the sparse drill holes. The cost of being wrong can be bankruptcy.
Outliers. These can be data rich and should if affordable be examined on an individual basis to see if they add to theoretical understanding of processes. They are common in gold deposits as “the nugget effect” where one half of a split core gives a hugely different analysis to the other. There are several treatments used, one being to truncate high values to n x the mean of surrounding values, where n is subjective or derived from experience elsewhere. Abnormally low outliers are seldom adjusted, but are often reanalysed.
In mining, the relation between an assay in a drill hole and the grade of ore extracted is fairly close when done well, because of a lack of perturbations. With temporal climate data, there is much literature showing the difficulty in even establishing a reliable time base, let alone the quantification of cause and effect in climate (do tree ring isotopes tell us climate at known past times as well as drill holes tell us ore grades? Nope). Virtually all climate reconstructions over about 100,000 years old rest on time bases that are extrapolated from a shorter time and one has to have immense faith in uniformiarianism and stationary processes and constancy of sensitivity and trace element and isotope analysis – even in the constancy of sunlight, which can never be extrapolated with confidence beyond the instrumental era.
In the mining example, the data build up as drilling proceeds so that one approaches an asymptote where the drilling of another hole and analysis of its core will scarcely change the final estimate of grade distribution. So maybe this is the way to approach the selection and combination of proxies. Using all means available, be they stats or corrections of scribal errors or eyeballing, start with the best looking study and then blend in the next best looking. As more are added, a preselected estimate of quality can be tracked until it reaches an unacceptable level. Stop there and start to draw conclusions.
Knowing when to start is one third of the problem. Knowing when to stop is two-thirds.
I have an idea. One should be able to find or construct some kind of statistical test that will do anything the eye does.
Re: Hank (#30),
The eye builds overfit models, because the human mind is a hard-wired pattern-matcher. That is precisely what you do NOT want to do with statistics – build overfit models. So, bad idea.
Interesting to read Ian Jolliffe’s latest comment at Tamino – I wonder if he has been reading this thread? http://tamino.wordpress.com/2008/09/17/open-thread-6/#comment-22556
Re: Patrick Hadley (#32),
The fertile mind seeks to interpret coincidence as pattern of greater meaning.
Re: Patrick Hadley (#32),
Ref Ian Jolliffe’s latest comment at Tamino
Very wise. Having worked through the transition from manual to computer data processing, we insisted that staff did manual plotting of geoscience data even when computers became the easy option (because they became the easy option). Why, even I did it.
Manual plotting brings the scientist closer to the data and improves insight. It’s a part of learning. It’s rather like medicos talking to patients rather than diagnosing entirely from printouts. Young guns can call it stone aged technique, but should try it first. Graph paper is still on sale.
Statistical models are an honest check on confirmation-biased pattern-matching.
Re: bender (#34),
Well, they can be.
Re: Sam Urbinto (#35),
… when tested in independent, out-of-sample trials.
Bring back the pirates! Arrr!
Willis, thanks very much for this post. I used PCA extensively in the social sciences for many years, and it was that experience that got be interested in the MBH saga before Climate Audit was even born.
In my applications the data were survey responses, not proxy series, but before I put anything into multivariate analysis I would spend many many hours inspecting the data, plotting histograms etc. I won’t bother with the detail, but I wanted to understand the data I was using, and to flag items that had unusual distributions (e.g. highly skewed, bimodal) that indicated problems with the way respondents were interpreting the questions.
I’ve been thinking about the problem of selecting some kind of “pre-screening” criteria to eliminate the bogus proxies. Certainly we need to get rid of the truly pathological distributions. Measuring heteroscedacity seems to work for that. But there are deeper questions.
1) Is there in fact a common signal across the 1209 proxies?
2) If so, which exact proxies have the common signal and which don’t?
To investigate this in a Monte Carlo simulation, I took the first thousand data points of the HadCRUT3 dataset. Modeled as an ARMA process it gives AR = .85, MA = -.42. I normalized the dataset.
I then created a hundred random normalized synthetic proxies, each with N=1000, with the same ARMA structure (.85, -.42). To 15 of them I added the HadCRUT3 dataset. From 10 of them I subtracted the HadCRUT3 dataset. I renormalized them all. Visually, there is no difference between datasets which do and do not contain the common signal.
Then I set out to design an algorithm that would automatically select the proxies which contain the signal.
Now, there’s likely established methods for this, but I don’t know any of them. So I used a brute force method that actually was surprisingly effective. Here is the procedure.
First, a repeating loop. I took a straight average of the 100 proxies. This, of course, gave me the raw common signal. I calculated the correlation between each of the proxies and the common signal. I removed the synthetic proxy with the smallest absolute correlation. I repeated that process, re-averaging to get the new common signal and re-correlating until all the remaining proxies had an absolute correlation of 0.2 or more to the common signal.
At that point, I stopped and inverted all of the remaining proxies which had a negative correlation.
Finally, since the inversion of the proxies changed the shape of the average and the correlations, I repeated the first loop again, removing proxies until all the remaining proxies once again have a correlation, between the proxy and the average, greater than 0.2.
This process is extremely good at identifying the proxies bearing a common signal. Starting with a correlation between the initial proxy average and HadCRUT3 of ~ 0.3, the process ends up with a correlation typically over 0.9.
Anyhow, that was my thought — that instead of taking a bunch of proxies and ruling some out based on heteroscedasticity, that we rule them out based on their contribution to a common signal.
And it is possible (at least in simulation) to disentangle which proxies have a common signal. Finally, my procedure also avoids the problem of data snooping. Using the procedure which Mann uses (proxy selection on the basis of correlation with local temperature) means that we no longer have a group of proxies which are “innocent” of the temperature.
More as my research progresses,
w.
Looking forward to seeing some more of your marathon research. Looks most intriguing.
Robin
I think this is off subject, but have you thought about investigating statistically the article by Douglas, Singer, and Christy on trophosphere that has been criticised on some blogs?
Well, they can be
thanx
kalejia
3 Trackbacks
[…] put each and every dataset to the eyeball test. There’s an example of what I mean in my post When Good Proxies Go Bad over at ClimateAudit. (Y’all should definitely visit ClimateAudit, Steve McIntyre is […]
[…] in the earth as temperature proxies. Willis on Hegerl :: Review of a paleoclimate reconstruction. When Good Proxies Go Bad :: Analysis of the proxies in the Mann 2008 paper on temperatures of the previous millennium. […]
[…] to believe that the results are “robust”. I thought I’d revisit something I first posted and then expanded on at ClimateAudit a few years ago, which are the proxies in Michael Mann et […]