Here’s an interesting calculation showing remarkable coherence between multiproxy averages of red noise, when proxies are shared.
Esper et al [2004], posted up here, removed low-frequency from MBH99, Briffa et al [2000], Jones et al [1998] and Esper et al [2002] and pointed out a seeming coherence, reporting an average interseries correlation of 0.42.
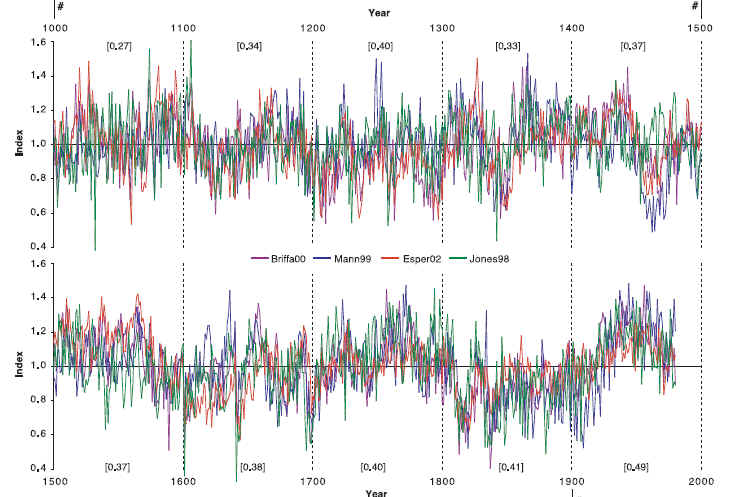
Figure 1: Figure 1 from Esper et al [2004].
However, many of the proxy series between these reconstruction are shared, as summarized in the following Table. Esper et al. discuss the fact that 2 series are in common, but do not consider or report on the additional impact of the 4 series shared by 3 reconstructions or the 4 series shared by 2 reconstructions.
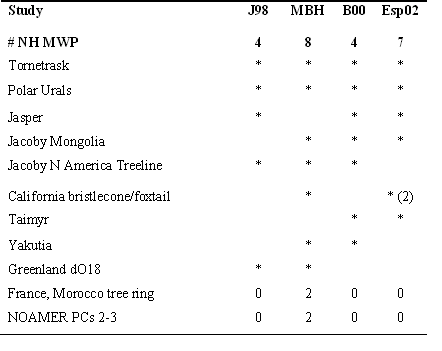
I did a quick simulation using of 12 series with AR1 coefficient 0.8 and then calculated multiproxy averages using the distribution of the above table. (There are 4 other series in MBH, which are very lightly weighted. I’ve not modeled this here, but will re-visit on some other occasion. Because of their light weighting, their effect is negligible.) The mean interseries correlation was 0.66.
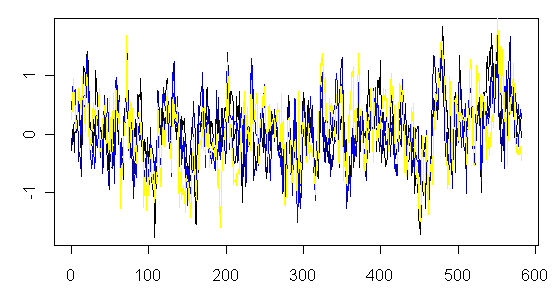
Figure 2. Simulation with Shared Pseudoproxies
So Esper et al [2004] have hardly established that the interseries correlation of 0.42 between these series is anything of statistical significance.




7 Comments
If you can’t tell it from random numbers then it doesn’t mean a thing.
Why hasn’t anyone performed sensitivity tests like this before? Are they afraid of the answer?
Re #1:
“Are they afraid of the answer? ”
This suggests another John McLaughlin type poll:
In your opinion the above post, along with many others on this blog, lead to which conclusion:
1 Steve McIntyre doesn’t know what he’s talking about.
2 Steve McIntyre is just too picky, he’s missing the big picture.
3 Scientists should never be scrutinized by experts in something so menial as mining shenanigans.
4 Some branches of Climate science aren’t really supposed to be science, they’re really an art of predicting the future.
5 There has to be a middle ground somewhere.
6 Scientists can’t be expected to learn statistics too deeply, that would make it harder to publish a seemingly robust finding.
7 The scientists knew the statistics at one time, but got rusty.
8 The scientists are just too burned out to deal with the more subtle statistics.
9 Some scientists have an agenda and realize that learning statistics too well could get in the way.
10 The Scientists knew the statistics so well, they knew how to make it very hard for someone to spot a problem. They didn’t run the above test because the answer did not matter to them.
Re #2
I go for a 7 on this one
Re #2
I think 9 is more realistic.
Can you disaggregate the issue of autocorrelation from the issue of shared proxies? It would seem that they are not identical.
It also seems that you ought to be able to come up with an algebraic formula that indicates the degree of “non surprising coherence”. C=f(ARIMA parameters, %proxies shared). Then you could look at higher degrees of coherence and see if they are higher, maybe even do some significance tests.
Somewhat off this topic, I noticed this referenced on junkscience. It appears to concern the difficulty of establishing the significance of trends in poorly understood natural systems. From the abstract:
It sounds as if the novel idea of applying proper statistics may be catching on.