Weaver says the next generation of his climate model will address the influence of climate on human evolution.
I guess we can expect headlines saying that scientists University of Victoria have shown that global warming, if left unchecked, will lead to the development of a third eye by the year 2075.




262 Comments
Very funny. I wonder whether they meant the developments of the society instead of the biological evolution of humans. 😉
At any rate, even this statement couldn’t hide too many meaningful predictions. If the weather is too hot or dry, people will be moving elsewhere, and so forth. But it is hard to imagine that he could predict any details with models that have serious problems even with predicting the overall features of the climate – e.g. the absence of warming in the Southern hemisphere’s troposphere and/or power laws determining the long-term persistence.
Sometime in the future, people will surely have better models that can predict some details. But it will only happen after they start to do serious science – which includes local science – instead of parameterizing everything in the world with one binary variable, the global warming, whose value “+1=YES” is treated as a pillar of religion.
Maybe after they model human evolution, they will try to predict weather.
I live in Oakland – average temperature 55 Degrees Farenheit.
In Los Angeles the average temperature is about 65 Degrees.
So I guess global warming will make us all more “Hollywood”. How horrifying!
I took a look at the UVIC site … among the “major improvements” in their new, you-beaut model are:
Here we are, it’s 2006, their model has been in use for some time, and just now the clouds are absorbing shortwave in both directions?
Well, I’ll sleep better knowing that.
Seem like these guys think that tuning the parameters, rather than actually including some science, is the way to go … in their defense, I’ll say that this is an “intermediate complexity” model, but even so …
Drives me spare. You want to see a real model? Take a look at GATOR-GCMOM …
What does GATOR-GCMOM have that none of the other girls have got?
So next time you read about climate model results, remember, that list above is the things that the IPCC models, as well as the University of Victoria model, don’t include …
w.
Any chance that these advanced climate models will help climate modellers stand up straight?
Or alternatively, be able to predict so much as the next couple of El Ninos BEFORE the event?
"Hydrometeor particles"? I’ve been inundated with those things all day…
It is a common technique in politics to scare the public in order to get them to your side. One of the main attraction of global warming is the “unknown” and “potentially unmeasurable global change and damage”. If I recall it was Lincoln who said something to the effect that ” you can fool all the people at a time, some people all the time, but not all the people all the time”. It seems the current trend seems for the warmers to upstage each other claims and in scaring the public into their views. I am looking forward to the next article on the “the last two decade being the warmest in the last 10 million years” followed by an article that the last two decade was the warmest in 100 million years”, then in the “last billion years”. I hope the climate modellers will not use racism and huge population movement to get the exteme right of the political spectrum into their side.
I think I remember a song from a 1970s movie called “Hydrometeor particles keep falling on my head”
Re #4: How about subbing in a link for that monster?
I see that the quote regards Mark Jacobson’s model. For those who don’t know who he is, Mark was the victim of the Bush administration’s first major and probably still most egregious abuse of science.
Also, Willis, the complexity issue aside, I think you’re comparing different types of models here.
Hello All, This is from Mr. welikerocks.
I wrote a paper on this very subject while in graduate school back in 1997. I took a grad course on Climate Change, funny the liberal teacher wouldn’t touch human influence on climate, said there was no real science to back it up. Anyway, It was very difficult to find any information regarding the subject, but after much work with lexusnexus and library assistance, I managed to find 7 papers dealing with the subject. Of those 7, 4 were not of much help as they only covered the Holocene to latest Pleistocene, maybe 20K yrs ago. Of the 3 papers that did cover substantial time periods (several hundred thousand yrs), all three were written by archeologists or teams of archeologists. The results were the same, As the climates warmed, human populations spread out, mostly into the northern latitudes. As the climate cooled, human populations were forced to move south again. This forced southern migration led to conflict (theorized) between competing human populations, and entire groups of humans disapeared from the fossil record. The conflicts were centered in and around the middle east/Isreal/Lebonon, which was where several of the study areas were located. It was theorized that the onset of glacial cycles forced the northern latitude peoples to move south, and they then came into conflict with the peoples who were already occupying those areas. In many cases the northern peoples completely eliminated the competition and or disposessed the peoples who were previously living there. The thesis formed were based on the human fossil evidence and said as the planet warmed, the northern latitudes once again became habitable and humans quickly moved north following game and plant food sources.
I say stop global cooling
#9 — Steve B., you’re in no position to fault others for abusing science.
#9 how about everybody abusing their positions during and after the last president left office? like the high ranking EPA officals erasing their hard drives when they were under court order not to do so? I remember because my husband worked for Cal. EPA at the time. Funny it’s around the same time frame as your link. http://www.junkscience.com/apr01.htm
” – “WASHINGTON – Electronic computer files of top Environmental Protection Agency officials under former President Clinton were erased in January, despite a court order to preserve records sought in a lawsuit by a conservative legal group. Craig Lawrence, an assistant U.S. attorney, told U.S. District Judge Royce Lamberth on Friday that the computer storage drives of former EPA Administrator Carol Browner and three of her top aides were erased by a contractor just before Clinton left office Jan. 20.” (AP)
Link to the law suit:
http://www.landmarklegal.org/DesktopDefault.aspx?tabid=160
Quote:
“”Environmental Accountability
After learning that many of the nation’s most extreme environmental groups have received billions of taxpayer dollars from the federal government, Landmark also initiated recent litigation against the EPA, the Forest Service, the Bureau of Land Management and the Fish and Wildlife Service aimed at exposing both the amount and misuse of federal grants by these organizations, including political advocacy and lobbying. The EPA has already produced a list of nearly 14,000 grants totaling more than $2 billion made to nonprofit organizations since 1993. “”
If that were to happen now, erased computers under investigation, belonging to this President, what would pray tell would we be hearing then? Sheesh.
Song by B.J. Thomas in Butch Cassidy and the Sundance Kid. Reminds me of the sequence where Butch and Sundance are pursued relentlessly for days by a posse. Butch finally turns to Sundance and asks, “Who are those guys?!” Doubtless the hockey team feels much the same way about M&M.
#13
And just like the guy who’s feet are too big for his bed, nothing [in climate science] seems to fit!
oh boy. lol 😉
Re 9, Bloom, you say:
Victim? Mark was a victim? There’s not a word in the text of your link that even mentions Mark Jacobson. He doesn’t even get an honorable mention for writing the paper that Bush presumably read. It’s all a rant about how we should have signed the Kyoto Treaty, because ” control of greenhouse gases, particularly carbon dioxide is necessary for reversing warming” … reversing warming? Did you read the link? Here’s their chronology
In May, Bush gets Jacobson’s paper about the dangers of black carbon. The sole and only mention of Kyoto in the paper is the statement “Under the 1997 Kyoto Protocol, no control of black carbon (BC) was considered.”
In June, Bush explains why the US won’t sign the treaty, and says we should focus on black carbon … and this makes Mark a victim how?
And how was not approving the Kyoto treaty an “abuse of science”? Remember, every single Senator voted against signing it. How is that abuse?
I definitely am comparing two kinds of models here, a scientifically based model, and tinkertoy IPCC models.
w.
It’s a fine evening for rants, I see.
#16 — Your example brings out the best in everyone, Steve B.
Steve M.,
Not sure if this is the appropriate thread to post this question. A commenter on another blog has suggested that your criticism that MBH mines for hockey sticks is false because your method uses an artificially high correlation coefficient
“The first defect is that Figure 9-2 is based on an artificially high correlation coefficient (phi) of 0.9. Real tree-ring proxies have a coefficient of around 0.15 and when you actually feed this value into McIntyre’s program (Appendix B of the NAS Report), the artificial hockey stick almost competely disappears in the noise. Was McIntyre worried that an honest choice of correlation coefficient wouldn’t have made an impact?”
I’m curious how you respond to this. Apologies if you already have.
cheers,
Marlowe
Re #18, Marlowe Johnson
Could I ask where this was posted ?
fFreddy,
It was posted over at William Connelly’s site,
I don’t even come close to having enough expertise to understand the finer points of this debate but on the surface his argument seems compelling, which is why I’m curious…
Re #20, thank you.
William Connelly – the blog host who dismisses the Wegman report on the grounds that one of his potty-mouthed commenters says that Wegman’s university used to do research work for Reagan’s Star Wars program … never mind the maths, let’s do some hating …
Just on first sight, the bit you quoted is talking about the parameter for an autocorrelated process, not the correlation coefficient, which is a very different thing.
Not to forget fFreddy, the statistical insignificance of MBH9x which Wegman agreed with; as did the NAS panel; as did Wahl & Ammann…
#18. Could you give me a more relevant URL to connolley?
It amazes me that, after all this time, so many climate scientists don’t understand some pretty easy stuff. One really wonders.
First, it’s not just Wegman that confirmed the bias in Mann’s method; the NAS panel did as well.
Second, the persistence in the North American networks is not AR1=0.15. This comes from some goofy calculates by Ritson using his own method for estimating AR1 coefficients, rather than a standard algorithm. I discussed this earlier and showed that this method broke down in the face of ARMA(1,1)- and most site chronologies are significant at that level.
Third, the impact of the Mann method on actual PC networks can be shown (and was shown) on actual PC series independent of AR1 estimates. The AR1 estimates were only used to illustrate the bias.
Fourth and perhaps most importantly, the impact of the Mann method was to overweight bristlecones. The ultimate issue is how much weight to put on bristlecones in a reconstruction. If they are downweighted using a conventional (covariance) PC calculation with 2 PCs, you don’t get a HS. Alternatively, if you follow the NAS panel recommendation and “avoid” bristlecones in a temperature reconstruction, you don’t get a HS.
It’s amazing to me that Mannians should be grasping at irrelevant straws like this, but I should have stopped being amzed a long time ago.
Steve,
Thanks for the clarification.
here is the link:
bah…I’m clearly useless with html tags, so here it is without..apologies John A.
http://scienceblogs.com/stoat/2006/09/the_missing_piece_of_the_us_cl.php#c229579
Average of Osborn&Briffa 2006 raw proxies gives one-lag acc around 0.7. Even if you try with 200 y windows. And if they mean that proxy noise gives 0.15, there will be another problem. A serious one.
Re #23
I would be careful about that ARMA(1,1) assertion Steve. Maybe you’ve done some additional analysis on the matter, or consulted a TSA guru, in which case, ignore my cautions. But I haven’t seen a convincing physical interpretation of the AR and MA coefficients yet. And of course it is possible to mathematically express any high-order AR or MA process as a mixed ARMA process (i.e AR(2) -> ARMA(1,1) -> MA(2)); that doesn’t mean it’s structurally (i.e. physically) more correct. The problem is that this rewriting changes the coefficient estimates drastically. Of course I’ve made these points before, and you already know alot of this sort of thing, so you have probably accounted for it all in your argumentation. This is just a friendly reminder to make sure you’re on solid ground on this one point.
#27. Fair enough. I agree with your caveats and it’s not a point that I’m relying on ; so I’ll make sure that any such comments are properly nuanced.
To clarify, the assertion I’m talking about is not that Ritson’s method breaks down with ARMA(1,1) processes (I don’t doubt that), but that tree ring proxies are better represented as ARMA(1,1) processes than AR(1) or AR(2) processes.
#25. One other point about the artificial hockey stick that’s even more relevant than the red noise argument and has emerged more sharply in the von Storch-Zorita discussion. Let’s suppose that you have a network with a real signal that is not a HS and insert one nonclimatic HS series in the network. The Mann method will pick out the HS series and invert the actual signal. I showed this graphic in Stockholm and von Storch grabbed the point instantly and said to me that it made sense (although he obviously hadn’t worked through the details.)
The bottom line, is it not, is that Mannian PCA mines for spurious “signal”, regardless of what generates that “signal”. The fact is ARMA(1,1) and (AR1) red-noise processes both have a lot of minable “signal” (=source of spurious correlation) in them – moreso when you crank up the redness factor, AR(1), to 0.2, 0.4, 0.6, 0.8.
RE: #9 – Steve B, enough already with the victomology. The generation who came of age during the 1960s and early 1970s are no longer outsiders, minority factions or victims. You folks now run the show! Good luck! And may you live in interesting times 🙂
#31. Exactly. But let’s say that the bristlecones are a nonclimatic trend due to fertilization of some king (CO2 or otherwise) or some kind of highly nonlinear response. The Mannian mines this even more than a red noise situation. The red noise situation illustrates the bias of the method. The bias at work is in the promotion of the bristlecones into the PC1.
Mannian regression also enters into the mix and has been much less described. Because the “proxies” are equivalent to noise, any HS series that enters from the PC module will imprint in Mannian regression as well.
RE: #10 – RE: Global cooling and utter disaster …..
When one sets aside biases and agendas, it is quite clear that climate changes involving warming are greatly preferable to ones involving cooling. Every past episode of warming has resulted in cultural growth and every past episode of cooling has resulted in a dark age.
RE: #34 – And yes, and quite controversially, given today’s cultural biases, I do personally consider the LIA to have a been a dark age. From an absolute standpoint, the chaos and overturning of stability during those times was immense. Ask anyone who was an aristocrat in France during the 1790s. Of course, revolutionaries and haters of order will disagree with me 😉
Thanks Steve and Bender for answering my question. It seems to me that you are making two points. First, the auto-correlation coefficient for tree rings in N. America is not 0.15, so O’Neill is wrong on that point. The second point seems to be a more specific criticism of MBH methodology, rather than what value to use for a particular input. Have I got it about right?
Re #35, Steve Sadlov
Harrumph … and we’re back on 1776 and all that …
Re#15-
Yeah, he didn’t do the best job of explaining why. He should’ve just pointed to the Byrd-Hagel Resolution.
#7
H.L Mencken said,
“The whole aim of practical politics is to keep the populace alarmed (and hence clamorous to be led to safety by menacing it with an endless series of hobgoblins, all of them imaginary.”
Scientists with a political bent do it even more efficiently.
#25
So what is so wrong with this article? Its good to see the acknowledgement in this article of Steve and Ross’s work.
“But the greatest credit must go to the unpaid Stephen McIntyre and his partner in this quest, Ross McKitrick. They are the ones who first blurted out: “The professor has no clothes!”
And sorry for the ad hom but who the f**k is Chris O’Neil?
KevinUK
#36. the criticism of MBH methodology holds regardless of what is an appropriate pseudoproxy model for tree ring chronologies (but I categorically deny that there is any basis for modeling tree ring site chronologies as AR1=0.15 red noise.) The only people that seem to want to dispute this are climate scientists; others understand it easily. But as always dont lose sight of the role of bristlecone weighting as being the active ingredient in the PC methodological issues.
Steve & bender (#31,#34): Since essentially the “spurious signal” is the bad apple which has the greatest absolute unsubstracted (overall-caliberation) mean, IMO another good way to demonstrate the Mannian PCA effect (with no correlations involved) is to use a “splicing/homogeneity argument”:
Climatologists are well aware of the homogeneity issues in instrumental series. Small changes in location of the station etc. can have a big impact on the mean. So generate, say 70, white noise artificial “temperature series” (use different means for illustration purposes, i.e., “locations”). Then one of the “stations” gets moved a bit (say to a higher location) around the beginning of the caliberation period, so “splice” the corresponding series by substracting (it’s better to substract than to add for the full effect 😉 ) a fixed value from all “measurements” in that series during the caliberation period. This creates a hockey stick with Mannian PCA (but unlikely with the true PCA), and climatologist know this could easily happen with “true” temperature series, so why not with proxies.
It is also always good to show the simple mean of the series, so people realize that the Mannian method truly “mines” for the hockey sticks.
Kevin, I think he’s yet-another-Australian who has problems of understanding basic statistics. I had argument with him about the hockey stick over you-all-know-which-Australian’s blog. I gave up after realizing that the guy is hopeless. Read the exchange I had, and you’ll see how much he has learned in last two weeks or so…
RE: #37 – Hahaha- Good point! 🙂
If the key issue is percent bcp, then you should lead with that, Steve. If you make a big too doo about algorithm mining from noise, then you need to keep the caveat that one DOESN’T use Preisendorfer’s n, for instance. You overplay your hand on things and in particular on your “flagship complaint”. You also have a tendancy to list things as “multiple flaws” rather then “flaws required to occurr together”. A perfect example is indicting “off-centering” by comparing Mannian PC1 to one from a covariance matrix. The problem is that this is not ONLY changing off-centering, it is also changing “standard deviation dividing”. Furthermore, it’s irrelevant for you to defend yourself with comments that “covaraince matrixes are ok”. You actually need to show that correlation matrixes are bad and covariance preferred, to justify holding up covariance as the relevant comparison for Mannian. I think this (your muddling factors) is a slight dishonesty/unfairness and a flaw in your logical thinking pattern.
And when challenged on a point, you become defensive, argumentative, rather then honestly objective and explanatory (as say Judy is).
And your readers need to watch out for that, to make sure they don’t get misled…
Re #45
He was asked for a response on a specific question, TCO. He was responding to the question. If he answered a question he wasn’t asked he’d be accused of dodging the question. His approach was correct. Answer the question directly in a first post. Expound in a second.
If you say too much in one post the warmers will accuse you of a “tap-dance”.
I have seen a pattern (as in what you called out in 27) of not keeping caveats in when needed and of them being left out in a manner which helps Steve’s case look stronger and Mann look worse. That was the thought connection for why I made the remark.
Let’s get back to the specific question from the commenter, though. Steve made the point that he thinks the true AR value of the proxies is higher then what Ritson sees (based on looking at calcs using an AR and MA model). When he ran the red noise experiment, was his red noise, AR and MA or just AR?
About climate models, I just finished reading the paper:
J. Ràƒ⣩sàƒ⣮en et al, European climate in the late twenty-first century: regional simulations with two driving global models and two forcing scenarios, Climate Dynamics (2004) 22: 13-31.
Gosh, see their control simulations (figures 2 and 3)! Seriously, in any other field, if your models are that biased, are they considered to be of any good?!?? And these guys don’t seem to care… on what Earth they were living during 1961-1990: over 80% cloudiness in Scandinavia… 4 degrees warmer winter in Lapland… almost no rain in Spain/Greece etc…? The highlight of the paper is just before section 4: they say that their models are of “comparable quality” as both of them have similar biases in many places! I guess the “CRU climatalogy” (as they call it) is just another computer simulation for them…
And the lead author of the paper is the only Finnish author in IPCC 4AR process … makes me so damn proud.
48. Agreed and I appreciate that clear, succinct communication may lead to some imprecision of the answer. I just don’t think it should be edited down in a manner that is biased (leaving out things that hurt Steve’s case and tending to keep those that help it.) Something to watch out for, IMHO…
I won’t say this is an answer to #36, because I may not have it exactly right. I will instead ask Jean S and Steve M if this is an accurate assessment:
1. To suggest the issue is a1=0.15 vs. a1=0.9 is to mischaracterize the problem by oversimplifying it.
2. An AR(1) model with a1=0.15 is an inadequate representation of NA tree rings. Some chronologies may behave that way – but not all of them, and certainly not the ones most responsible for the hockey-stick shaped PC4.
3. The ARMA(1,1) model that Steve M describes here is a better fit to the tree ring data. If a1=0.9 in this model, that a1 is not directly comparable to the a1 in the AR(1) model because there is now a second parameter, b1, that must be considered as well.
4. The ARMA(1,1) model, whatever its parameters, will produce red noise that can easily be mistaken for signal. The greater the magnitude of a1 & b1, the more that is true.
5. Mannian regression mines for signal. And red noise processes, be they AR(1) or ARMA(1,1), can produce hockey-stick-like patterns that contain no real signal (they’re noise, after all).
6. These signal-like noise patterns, although produced by a red noise process, may be correlated with a signal-containing time-series, such as the instrumental temperature record.
Steve M’s analysis is therefore relevant.
*It is worth noting that a white noise process is capable of generating ANY pattern. It is exceedingly unlikely that a single sequence of 1000 random numbers will generate a hockey stick. But it could happen. Increase the number of samples from one to a million and you might start getting a few hockey-stick shaped sequences. A red noise process just increases that likelihood. The point is: Mannian regression mines for these. Turning down the ar1 means you just have to mine harder to get the preconceived pattern you’re looking for.
If O Neill is assuming that Steve M’s argument hinges on the proposition that tree-ring chronologies tend to be AR(1) in structure with ar1=0.9, he’s flat wrong.
When Steve ran his experiment, did he use (0.9,0) or did he use (0.9, something)? It seems to me that if he is going to make the point that 1,1 modeling gives you a higher first coefficient, then he needed to use a two coefficient type noise in his pseudo-proxies. Of course the converse would apply to Ritson/Connely if Steve did use a two coefficient noise proxy set and they are comparing it to a one coefficient set.
I’ve actually always felt that a more common-sense thing was for Steve and Ross to indicate what shape (define it mathematically) interacts with the method to get promotion. He tends toward this thinking with some low frequency comments…also the Wegman experiment is intrigueing in showing that the interaction is not per se with hockey sticks but with any clear long term (low freq) curved shape. Does the method mine for hockey sticks or some shapedness in general?
And it definitely doesn’t mine for non climactic signal or not. It has no way of knowing what is good or bad signal. The method can’t tell if the bcps get their shape from dry lakebed blowing with sheep leaving the pasture while CO2 fertilizes their happy rings…or if the bcps have some magic teleconnection to the NH “global climate field”.
Once we understand and agree from a mathematical point of view, what exactly the method DOES, then we can discuss if what it does is fair/relevant or not. If I use a polling or market surveying technique and it is very biased, then of course it is not relevant. If I’m looking for enemy subs in a busy shipping lane, then separating and displaying some select “signal” separate from noise is relevant. Even in basic polling or market surveying some transforms on the data that are more complex then simple sampling and averaging may be relevant (for instance norming to the correct population by segmentation or shading the numbers based on records of voter turnout or the like). But the key thing is to separate out the simple description of what happens mathematically from the slanting and positioning debate efforts.
re #52: Strong comment. One thing to add for Marlowe and others (I try to explain this without math terms):
IMO it is important to understand what PCA is supposedly used for in MBH (and elsewhere also): to compress information. Instead of dealing with 70 North-American tree-ring series, you use PCA to produce, say, 3 series that are weighted linear combinations of the original series and capture the main “descriptive” features from all 70 series. Now if only few series (bristlecones) have an exceptional pattern (hockey stick), this does not appear in normal PCA in those top PCs as it is not “descriptive” feature of most of 70 series. But Mannian PCA picks that feature by assigning a big weight to all series that contains the desired feature.
So it is not the correlation properties that creates hockey sticks, but as bender explained, noise processes with autocorrelation (AR) are more likely to produce series which has the right property (as bender also said it can happen with white noise but it is unlikely). In MBH the bristlecones have the right property. See also my comment #42 how to obtain from white noise a series with the right property.
TCO (#53), these are all explained in Wegman’s Appendix. I don’t know if the explenation there is clearest possible, but all essential mathematical facts are there. The key property is the difference in means in the caliberation period (blade) and the rest (bar).
I’m still a little lost as to what the benefit of PCA process (information compression as with a zip file) is in the general process of training proxies and evaluating the output. I see how PCA is great for things like a chemical nose from Nate Lewis. For pattern recognition and categporization and perhaps investigatory analysis, PCA is useful. But for prediction?
53. Did Steve use one or two coefficient noise model proxies in his modeling of the mining?
#56: TCO, I’m sorry but I think I can not help you. I’ve several times tried to explain you the MSE-optimal approximation property of PCA. I may be a poor teacher but at least I’ve done my best.
JeanS, understood, please don’t give me another explanation of what PCA is, when what I’m interested in is a discussion of how suitable it is for the objective in mind. Feel free to answer number 57.
Re #59
Jean S answered #57 already (and with that #53a). He said the answer is in Wegman’s appendix. So go look it up and tell us!
Re #57
In the GRL05 paper M&M used an AR(1) red noise process where ar1 was calculated from the 70 series in the NOAMER tree ring data set. IOW there was a range of ar1’s, not one value, and they were fully representative of the spectrum of variaiblity in the MBH papers. They did 10,000 simulations which provides adequate opportunity for the “unlikely” randomly generated HS to show its face.
But, of course, you knew that – having “read” the entire blog. 🙂
Bender:
I think JeanS was referring to 53b, with the comment on Wegman Appendix. Nevertheless, I have just looked through that appendix and can’t find the answer to 53a/57. The closest I could find was part C (the summaries of the 2005 MM papers). There are a sentence or two talking about using red noise to test the transform. However, either the answer (single or double coefficient) is not in there or there is some phraseology that I don’t understand. So my question remains.
I also looked at the 2005 GRL paper itself and could not figure it out from there. I’m behind a firewall, so I can’t get to the ftp site for the paper’s SI. I will look a bit on the site. Maybe Steve discussed it in the context of one of the Ritson arguments.
We are cross-posting.
1. Thanks for the response on the AR(1) versus ARMA.Can you please tell me where you found this described?
2. As you pointed out, one would expect to have a different coefficient when 2 coefficients are solved for rather then one. (Same idea as multiple correlation regression work.) I’m a bit concerned about Steve defending his AR(1) value by explaining how a higher number is obtained when one models the tree ring series as (1,1), since he did not use 1,1 series as the input for his red noise experiment.
Re #62
I assume this was a crosspost with #61, which describes GRL05 methods.
section 2
Re #63
I *think* your concern is valid. Not certain. I’m looking into this, but suspect Steve M is as well.
*Note this does not make the O Neill argument correct. It is wrong. What the issue is is whether Steve has given a complete, debate-ending answer to Marlowe Johnson. Or just more fuel for the fire. Am investigating.
That’s great that Steve is researching things, but he could have just answered the question immediately (did he use a single or double coefficient method). It would be understood that argument over inferences may take a while, but he should be willing to answer questions of fact on things that we can all agree on. This kind of hesitancy to phlegmatically answer a factual question bothers me a bit. It reminds me a bit of you know who (not Voldemort). It’s not behavior of an ideal truth seeking and telling scientist.
A quick scan of GRL05 indicates the ar1 coefficients of the 70 NOAMER series are not described in the paper. [Presumably that’s part of the auxiliary material, available online. (Hurray!)] So I don’t have the bcp or HS statistics in front of me at the moment.
However … I think it is a mistake to characterize the bcps by a single ARMA model. I think you need two models because of the incredible change in behavior at the shaft-blade joint. i.e. A global ARMA model applied to the whole bcp series misrepresents the actual time-series structure. If you did that, the AR(1) for the blade would surely be on the order of ~0.7-0.9. This point alone is sufficient to refute O Neill and vindicate the M&M analyses. In fact, a red noise assumption is conservative compared to the real situation, and therefore stacks the deck *against* M&M – and yet their method still succeeds in showing the vulnerability of Mannian regression to spurious correlations under red noise! That’s robustness for you.
Re #67
“Hesitancy?” You got an answer within half a day and you’re complaining? You’re not too demanding, are you?
Here you go again on this same libelous crap as always. One day, and promise broken. Do you know how foolish you sound?
Bender, I’m getting confused in all the posting back and forth.
1. What does 65 mean (section 2 of what?) I looked at WEgman report. The appendix is A, B, C. The regular report has a section 2 that is essentially definitions.
2. Yup, I also looked at GRL paper (62 second para) and could not find the type of process described. As I said, I’m unable to get to the ftp site for the SI info (I think from my firewall).
3. Are you still firm that the process was AR1, not 1,1 as posted in 61? If so, what is your source? If I need to do a treasure hunt on the blog to satisfy your fiendish pleasure, let me at least know that it’s on there…:)
Re #70
section 2 GRL05 indicates they “applied a method due to Hosking (1984) to simulate trendless red noise based on the complete autocorrelation function”. To me that implies AR(p) where p is as high as what is needed to simulate the series. Would have to see the code and run it to know what p is. There are presumably 70 p’s – one for each series. Are most of them p=1? Probably, but probably with a few 2’s and 3’s. Main point, though: this is NOT an ARMA(p,q) model. It is an AR(p) model.
I will have to look at the EE papers to see what they say. I am scanning Wegman as we speak.
Wegman/NAS Figure 4.4, p. 33 recapitulates the M&M EE arguments using AR(1) with ar1 = 0.2.
GRL05 appears to be a meaningful refinement by extending AR(1) with low ar1 to AR(p) with realistic arp estimated from NOAMER.
#71 – it was an ARFIMA model – in using an arfima model, I was influenced by Mandelbrot’s observation of long-term persistence. But nothing turns on this and it was probably a needless complication and is not necessary to illustrate the effect. If one simply used AR1 coefficients from the function arima(x,order=c(1,0,0)), you get a HS effect from red noise. There’s no reason to believe that tree ring chronologies are AR1 processes. Ritson has a goofy method of estimating tree ring coefficients; it was discussed here http://www.climateaudit.org/?p=687. realclimate cut off discussion of Ritson coefficients in a record time of 7 days when they started getting humiliated.
As to the purpose of a PCA analysis in tree ring networks, the onus of proving this methodology rests with the proponent. In experiments with pseudoproxy networks which I’ve reported on here, I can find no circumstances in which the signal occurs in a lower PC which calls into question whether Preisendorfer’s Rule N – a rule formulated in a completely different context – is relevant. Also Preisendorfer always said that Rule N was a necessary condition for significance not a sufficient condition – realclimate always does sleight of hand here.
Re #73
1. I think I’ll take Yule over “Ritson’s Custom Solutions” any day. (Whoops – that’s an appeal to authority.)
2. Have you plotted a histogram of the ar1’s for the 70 NOAMER series? Under AR(1) and ARMA(1,1)? Alternatively, is the NOAMER dataset readily available somewhere where I could do this?
Re #73
TCO, that Ritson thread Steve M cites is another example of one I somehow missed, by scanning rather than reading.
Bear with me, Steve: ARFIMA means AR (1,1,1)? or AR(1)?
1, 2 or 3 coefficients in your red noise?
75. That’s ok. At least you have more good reading waiting for you. I have already sailed to the end of the universe. Now I have to watch it expand into the ether.
Re #77
TCO, it’s possible even that p,d,q, in ARIMA(p,d,q) are not fixed, but free to vary among the 70 series. His point, though, is that it doesn’t matter model what you pick; his results are robust, and Ritson’s goofy method falls apart as soon as p+q gt 2.
#74. The 70 sites in the AD1400 network (a subset of the 212 site network) with more bristlecones in the subset is here in the MM05a SI ftp://ftp.agu.org/apend/gl/2004GL021750
#76. TCO, I’m not going to explain arfima to you. It’s fractional differencing and the math is difficult enough for me. You can google fractional gaussian processes and amuse yourself if you want or read the citations in MM05a e.g. Hosking, but, for what you need, stay with AR. Again, you’re turning inside-out on an issue that is really secondary for the effect. At the time that we wrote the article I hadn’t thought about the issue of the impact of one nonclimatic series on a network – the point that’s been clarified from the VZ exchange – but it really illustrates the salient effect better.
Re #80
Thanks! (Patience, TCO. Graphic coming right up. Gimme 1/2hr.)
80. Steve, I won’t trouble you for any explanations of ARFIMA. You are released from TCO tutoring on that point. Bender can spoonfeed me or I’ll go learn it myself, if it is critical to understanding the issue. My only question for you was if you used 1, 2 or 3 coefficients in your red noise input (as both Bender and I were having a hard time noodling it out from the paper). Any way, thank you for clarifying that it was ONE coefficient (hope I got that right).
The code is archived. ONe of the reasons for archiving code is because with the best will in the world, explanations are not always clear (See Gary King for many comments on that.) I used the function hosking.sim for the ARFIMA simulations, but the code also includes code for AR1 simulations (which is what we’d done originally in the Nature article and what the replicators have done – NAS and Wegman.) So once again, you’re better off to follow the example of NAS and Wegman and experiment with AR1 (one coefficient) or perhaps ARMA(1,1) than ARFIMA.
The existence of this effect has been confirmed by both the NAS and Wegman panels. It’s the only thing that they both replicated. I’m not really prepared to spend any more time tutoring people on it.
Understood that you ran single coefficient. Thanks, Steve. The wider implications are of course interesting, but I needed confirmation on that matter of fact before moving to next level of thought.
Be careful what you think that you’re understanding. We ran AR1, but the illustration in MM05a is from ARFIMA which is not one coefficient. Wegman and NAS ran one coefficient. If you look at the post on the Ritson Coefficient, you’ll find information on AR1 methods.
Perhaps cigarette smoke and will be included in the next generation models.
GORE: CIGARETTE SMOKING ‘SIGNIFICANT’ CONTRIBUTOR TO GLOBAL WARMING
Fri Sep 29 2006 09:04:05 ET
Former U.S. Vice President Al Gore warned hundreds of U.N. diplomats and staff on Thursday evening about the perils of climate change, claiming: Cigarette smoking is a “significant contributor to global warming!”
Gore, who was introduced by Secretary-General Kofi Annan, said the world faces a “full-scale climate emergency that threatens the future of civilization on earth.”
Gore showed computer-generated projections of ocean water rushing in to submerge the San Francisco Bay Area, New York City, parts of China, India and other nations, should ice shelves in Antarctica or Greenland melt and slip into the sea.
“The planet itself will do nicely, thank you very much what is at risk is human civilization,” Gore said. After a series of Q& A with the audience, which had little to do with global warming and more about his political future, Annan bid “adios” to Gore.
Then, Gore had his staff opened a stack of cardboard boxes to begin selling his new book, “An Inconvenient Truth, The Planetary Emergency of Global Warming and What We Can Do About It,” $19.95, to the U.N. diplomats.
(My apology if this has already been posted)
Sent in from bender. (These appear to match my own calculations BTW)
Re #87
These are the AR1 and MA1 coefficients for the ARMA(1,1) model (top) and ARMA(1,0) model (bottom) fitted to teh 70 chronologies in NOAMER data.
Steve, ok, I think I got it now. the GRL article illustration is 3 coefficient.
Re #89
You haven’t got it. Your answer is not in the article; it’s in the code referenced by the article. Stop flinging crud to see what sticks. You may well be asking an ill-posed question – as I’ve told you several times now. The answer to your question, if you could pose it properly, is in the code. Who’s to say the order doesn’t vary among the 70 chronologies? The ultimate point, though, is that your question is irrelevant – as the graphic above shows.
I found a good “spoonfeed TCO site” http://www.vias.org/tmdatanaleng/cc_timeser_arima.html
(Steve, this is ‘tween me and Bender. You are off the teach TCO task.)
Or, you could download “R” and type help(arima).
Bender (Steve is on sabbatical), is ARIMA same as ARFIMA?
I thought this thread was about computer models. You have been successfully led away. I wonder why?
It’s all part of my evil plan to write nasty editorials about you in Canadian newspapers.
So getting back to the inquisition, Steve. Was it a 1,1,1 pdq model used for the GRL article?
Re #93 I don’t know. I would have to read that 1984 paper cited by M&M05 on TSA in hydrology to figure out what he was doing with ARFIMA. Presumably the F stands for “fractional”. Not sure what exactly that might refer to. ARFIMA might be a specialized term used in hydolorgy, or maybe I’m just unaware. ARIMA allows for differencing. Presumably that’s not the same thing as “fractional differencing”.
Re #94
Marlowe Johnson led us astray in OT post #13.
#96 is verging on moronic.
No. It’s not. It could be 2,1,1 or the like.
I’m not sure that reading the paper would tell you the answer. The GRL paper did not even say that it was ARFIMA. And when asked about code and the hoskins function, it seemed to cover both AR and ARFIMA processes. I think some of this discussion would have been nescessary to figure things out. For instance, you made a comment that he was AR1 in the GRL article, but Steve now says that he was ARFIMA…(contradicting what you said)
Re #100
1. I have told you numerous times now: the exact answer is in the code. I haven’t looked at the code, haven’t run it. Therefore it is not known whether your question is even answerable or not. It may be that p,d,q vary among the 70 chronologies. I’ve said this how many times now? You don’t get it.
2. #61 is incorrect. Thank you. I am 100% aware of that. I was the one who told you so!!! First in #68, and then a further clarification in #71.
You want answers fast & accurate. You can’t have both. Because it takes time to look up answers. So you can can the “bender was wrong in #61” routine. Bender was fast in #61. Bender was right in #68, #71, #72, #79, #87, and so on. If bender is fast, available, and hitting on 7/8 cyclinders, that’s better than most. You have no right whatsoever to complain.
Here is a good paper on ARIMA versus ARFIMA. pascal.iseg.utl.pt/~ncrato/papers/ncrato.pdf
Essentially ARFIMA is ARIMA except that non-integer values of I are allowed. I don’t think we need to worry about what a fractional derivative means. Essential thing is that Steve is telling us when he says that he used ARFIMA that AR, MA and I are all greater then zero. So it is like a 3 or 3+ coefficient model.
Relax dude. It’s ok that you were wrong. I just want to make sure of what right answer is. I saw info that went the other direction, but did not see a direct clear correction (and you were so authoritative with the first remark). I’m not trying to pound you. Don’t be so sensative. Just trying to make sure that we get things right. Obviously, my bulldog sticking to details has some relevance, has some value…maybe it’s not so stupid, given that there can be confusion, or incorrect info.
And maybe, don’t be so quick to send me to the Wegman appendix. The dope ain’t in there either…
Re #102
That’s what I figured. (For monthly flow data you might want fractional differncing. For annual data, no need.) But, you see, I didn’t want to be quick with my reply for risk of being wrong. Get it? There’s tradeoffs.
101-1: based on Steve’s comments, the posted code itself might not be adequate unless it says exactly with code was used for which figure. Steve seems to make the comment that looking at the code, we will see both AR and ARFIMA routines in that code.
104. It’s ok, man. I think it’s better if there is a caveat when you know you are guessing, but it’s ok regardless. Let’s just track down the right answer. A little less beating me up when I push, to verify things would be nice (but not required…I won’t back down to you or Steve, no matter how dumb you call me, if I have a doubt on an issue.)
I didn’t send you to the Wegman Appendix. At 2:33pm I pointed out Jean S’s post suggesting that. At 4:49pm I pointed out the use of AR(1) in Wegman Fig 4-4. Here you are complaining again about people helping you with your problems. Tell me: why should I ever help you if you’re just going to complain that I get things wrong?
1. AR(1) was used, but just not in the GRL paper.
2. The Wegman paper was the correct source for the use of AR(1), but not the Appendix.
These “errors” are trivial in my view. I will make those kinds of “errors” quite frequently because I don’t have instant recall of exact details, and they’re easily ironed out prior to publication. What I have is keen inuition about broad issues in pattern analysis.
And, yes, I’m sensitive about this because I see what you do to Steve M, hounding him all the time, and the names you call people like Pat Frank – and I don’t want the same treatment.
TCO – Huybers had no trouble with implementing the code; nor did Wegman; nor did Wahl and Ammann. The options are clear; you can generate the figures from the code. If anyone’s ever been in doubt about any step, they could re-trace the steps. Everything’s been on the table. Your constant complaining is really tiresome. Tell you what – go try and replicate a Team study and then see if you still have any complaints.
Re #105
You’ll never know what’s there until you look.
Relax. I’m not going to tan your “shiny ass”. P.s. yes you did send me to the appendix:
Re #106
I’m always guessing.
Re #110
I know what I wrote, I cited it myself.
I don’t see anything worthwhile in reacting to in post 108, Steve. I wanted to know how many coefficients you used and you have told me that you used an ARFIMA process. No need for me to look at the code. Your answer already tells me that you are at least 1 in AR and MA and some fraction in I. It’s good enough. Thank you for answering my question. I’m sure it would be good for my soul to look at the code, but since you answered me on the blog, I will just be happy with that.
OK, TCO, your last deleted comment is out of line. Please call it quits for tonight.
Steve, I will honor your wishes and leave for the night, if you really want it. How about taking another look and reconsidering. I thought my remark was more temperate then the 113 remark (still standing) about me being a secretary (I didn’t even call him anything back, just played along and called myself a secretary). My only point is that if I am pursuing an issue where things don’t add up (or I’m not sure that they do, or I even have a little teensy wondering if they do), that I’m not going to be scared or even bothered if people call me a fool or a “secretary”.
P.s. This ARIMA/ARFIMA paper is interesting.
P.s.s. Cross-posted at deltoid.
(If I don’t see this post go up or I don’t hear you change your mind, will honor your wishes.)
Steve, now you’ve eliminated Bender’s post (after my request to put my post back). Please put them both back. My remark was temperate and (as the injured party) I’m quite robust enough to withstand Bender’s little gibe. I really thought it very minor anyway. We’ve had a lot of useful ARMA, ARFIMA discussion. So it’s not like we are just goofing off. There is also a larger issue of how much I push on points and if I’m being overbearing or if the community is trying to stop me from pushing a (very few) very minor points where you may (possibly, in theory, conceptually, in a blue moon) be vulnerable.
(cross posted)
#4 Willis Eschenbach, I looked at the link about the model. I really like how it links regional effects with global effects by combining models of various orders of resolution.
TCO, I hadn’t noticed the post to which you took offence and when you pointed it out, I deleted it as well. You’re wasting bandwidth with this silliness. If you want to play silly cross-posting games, then go discuss things there. Yes, please stop posting tonight. You’re monopolizing the bandwidth.
Re #86: Source for that?
#52
Yes. RC post on the topic says that proxy noise a1 is 0.15. Proxy a1 is different thing. Maybe 0.9 is too large, 0.6..0.7 might be closer to truth.
This applies to Osborn&Briffa2006 proxies as well. And simple average of those 14 proxies gives a1=0.66, for the era before industrialization.
But the R code for figure 9-2 uses AR(1) with p=0.9, right? ARMA(1,1) or ARMA(2,1) would make some sense, the former can be thought as a sum of white noise + AR(1) and the latter AR(1)+AR(1). If the proxy noise is white, choose the former, if red choose latter. But these are just models, so need to be careful.
I think that the one-lag acc (AR(1)) estimate is important, whatever the underlying true model is. That is, the estimate you get by assuming that we have AR1 process. That’s how I would define redness, not sure if it is the right way.
I would appreciate a simple answer to the question,
. I am slogging through the code on the ftp site, but it is tough going. Not sure if the answer is in the text (cryptically) or if I need to use the hoskins simulator (and is there only one hoskins simulator?)
87 is interesting. It would also be nice to see what ARIMA (1,1,0) looks like. Is this implicitly what Ritson does? If (1,0,1) is “better” then (1,0,0); is (1,1,0) also “better” then (1,0,0)?
The Crato and Ray paper:
pascal.iseg.utl.pt/~ncrato/papers/ncrato.pdf
is fascinating.
In addition to teaching what ARIMA, ARFIMA, etc. are (very easily, with little of the pain Steve said was required), I abstract the following inferences:
1. It is easy to mispecify processes as ARIMA or ARFIMA when they are not.
2. ARFIMA is the most general formula, but will NOT converge to ARMA or ARIMA special cases (corollary to (1)).
3. Article overall seems a bit negative and cautionary about ARFIMA (corrolary to 1 and 2).
4. anti-corrolary of above, article says you need at least 100 oversvations, so the proxy set should have that, if it is made up of records going back to 1400 from 1980 in annual steps. So Steve passes that step for using ARFIMA.
5. With the above in mind, it would be interesting to see “to what extent that mining exists” when one uses an ARMA, ARI, AR, or ARIMA model rather then ARFIMA. I have no doubt, it will still be there, but have a sneaking suspicion that ARFIMA is the choice that makes it look worse. (I learned this with the covariance/correlation matrix kerfuffle. With arguable cases, both ways, Steve will show the one that makes his opponent look worst.)
TCO, honest question, can you tell me why you are so obsessed with such a miniscule detail?
Re #123 (5)
That is a breach of blog rules – impugning motive. A more reasonable explanation is that Steve used a method that he was familiar with from the hydrology literature. And it is also possible, even likely, that he used an ARFIMA model with fractional differencing = 0, in which case it wouldn’t be any differnt from ARMA. You don’t know what you’re talking about TCO. Why Steve lets you continue posting here is beyond me.
Re # 102 & 104 Bender & TCO The way to look at the fractional difference is to apply the binomial expansion theorem on it. See where that leads you.
The correct response to TCO’s insulting irrelevance and attention demanding tantrums is to simply ignore them. TCO is not a single person, but rather a group effort. That is why “he” seems not to learn–think of it as a slow witted tag team.
TCU,
The individuals making up the TCO tag team are individually annoying and individually irresponsible. So figure out which ones are abusing the TCO brand and reform them. TCO may be a corporate entity, but that does not absolve it or individuals that comprise it of corporate responsibility to the CA community.
tco – you can’t keep monopolizing the blog with tutorial demands or keep hijacking threads. You’re now taking over thread after thread with the same sort of stuff.
If you want to discuss Ritson coefficients or tree ring persistence properties, do it on a relevant thread and see if you can revive a discussion with someone else. You haven’t even read the references to MM05a on modeling persistence. Please read Hosking, J. R. M. (1984), Modeling persistence in hydrological time series using fractional differencing, Water Resour. Res., 20(12), 1898– 1908, cited in MM05a, before you comment further. Please read the references in Hosking as well. It’s not very easy – which is why I’ve urged you to consider the effect in an AR1 context where it also holds, as has been confirmed by both panels. I discussed stochastic processes yielding autocorrelation with you a year ago. This post http://www.climateaudit.org/?p=382 was specifically in re sponse to a question from you about stochastic processes that could yield series with autocorrelation properties.
Tree ring site chronologies are not generated by AR1, ARMA(1,1) or ARFIMA models, but by some complicated mechanism that is not understood very well and an interesting topic for study. The persistence properties depend as much on the author doing the study as the trees. The only purpose of obtaining persistence properties was to obtain pseudoproxies that were more realistic than the ones in MBH. If someone else wants to propose even more realistic pseudoproxies, then good for them. None of this affects the bias properties of Mann’s PC method. The yield of 1 and 1.5 sigma hockey stick shaped series will vary depending on the persistence – that’s all. Also as I’ve said lots of times, the more salient problem is the impact of a nonclimatic HS on a network – the issue arising out of the VZ comment. It wasn’t an example that I’d thought about at the time of MM05a, but is a more salient illustration – but it doesn’t affect the red noise example (which has been confirmed by numerous groups.)
I’ve done what I can for you, so please don;t count on further time from me. I’ll have to limit your number of posts pretty soon, so if you’ve got something to say, try to do it more systematically.
Re #126
No thanks.
Re #127, tcu
Intriguing. Could you clarify ?
re: TCO
If true that TCO is a corporate effort it explains a lot. And does this mean that TCO / TCU are an indication of where this is going on? It would certainly seem that TCU is someone who was in on the operation or had gained first-hand knowledge of it.
So does this mean that TCO has passed the Turing test (or that CA has failed it?) In my own defense I’d point out that I raised the question early on as to what sex TCO was, but I admit that I hadn’t considered that the denial by the TCO entity didn’t disprove female involvement (though it sounds like something a fraternity might come up with.) OTOH, I’d most likely be a science-club group or something.
Re #132
But the tag-team effect would not explain, or excuse, yesterday’s inanity. The time-scale of response was so fast & the exchange so continuous it had to be one person. That player needs to be reformed.
Next time I want to criticize Steve, I’m just going to use the TCO brand. It was bender, after all, “TCO”, that spotted the subtle gap in Steve’s reply to the Marlowe Johnson post – not TCO. TCO was asleep at the wheel. Bad TCO.
Re #133
bender rings in on ARMA(1,1) issue at 11:03am here:
TCO at 1:16pm, 2hours later.
Bad, tardy, TCO. Useless without bender’s vital assistance.
Re #130, bender, I saw the binomial expansion used in a literature paper to describe the fractional difference a few years ago. Your comment made me review my complex variable math book, and perhaps a Laurent Expansion using a binomial expansion would have been a better description. Further review suggests that the complex variable expansion may not be valid for a fraction (noninteger), but will check another book at work. So, then how does one mathematically describe the fractional difference?
Mandelbrot, who pretty much invented fractals, developed some of his ideas from looking at climate series – e.g. Hurst’s Nile River series. He even considered some of the tree ring series including precursor series in the NOAMER network. He had several articles in Water REsources Reseach in the 1970s.
Re #136 & 130, Steve & bender, my question for bender was, what is the difference equation for the fractional difference of the form (1-z^(-1))^(n) where normally we use n=1 but for fractional difference n might be 1/2 or 1/3, where z= exp(jwT) (z-transform). The binominal expansion provides a difference equation if the expansion holds.
I’m not TCO
That was me, see anybody can claim they are somebody on blogs.
#137 Phil, I think you’re confused about the algebra. The equation for fractional differencing involves the binomial expansion of [ tex](1-B)^d [/ tex], where [ tex] B [/ tex] represents the “backshift” operator. The actual vector of time series does not appear in this part of the equation. For positive values of [ tex] d [/ tex], one gets a finite-length ([ tex] d+1 [/ tex], actually) vector of coefficients. To get the d-th difference for the i-th element, one multiplies this vector by the vector of length [ tex] d+1 [/ tex] of the lagged time series starting at element i. For non-integer [ tex] d [/ tex], the vectors are of infinite length but everything else remains the same. Hosking [Water Res. Res. 1984(?)] does a nice job explaining this.
TAC, you need to remove the space after the “[” to get it to show correctly, viz:
#137 Phil, I think you’re confused about the algebra. The equation for fractional differencing involves the binomial expansion of![(1-B)^d [/ tex], where](https://s0.wp.com/latex.php?latex=%281-B%29%5Ed+%5B%2F+tex%5D%2C+where+&bg=ffffff&fg=000&s=0&c=20201002) latex B [/ tex] represents the “backshift” operator. The actual vector of time series does not appear in this part of the equation. For positive values of
latex B [/ tex] represents the “backshift” operator. The actual vector of time series does not appear in this part of the equation. For positive values of ![d [/ tex], one gets a finite-length (](https://s0.wp.com/latex.php?latex=d+%5B%2F+tex%5D%2C+one+gets+a+finite-length+%28&bg=ffffff&fg=000&s=0&c=20201002) latex d+1 [/ tex], actually) vector of coefficients. To get the d-th difference for the i-th element, one multiplies this vector by the vector of length
latex d+1 [/ tex], actually) vector of coefficients. To get the d-th difference for the i-th element, one multiplies this vector by the vector of length ![d+1 [/ tex] of the lagged time series starting at element i. For non-integer](https://s0.wp.com/latex.php?latex=d%2B1+%5B%2F+tex%5D+of+the+lagged+time+series+starting+at+element+i.+For+non-integer+&bg=ffffff&fg=000&s=0&c=20201002) latex d [/ tex], the vectors are of infinite length but everything else remains the same. Hosking [Water Res. Res. 1984(?)] does a nice job explaining this.
latex d [/ tex], the vectors are of infinite length but everything else remains the same. Hosking [Water Res. Res. 1984(?)] does a nice job explaining this.
Oops, you need to remove the space after the “/” as well … second try …
#137 Phil, I think you’re confused about the algebra. The equation for fractional differencing involves the binomial expansion of , where
, where  represents the “backshift” operator. The actual vector of time series does not appear in this part of the equation. For positive values of
represents the “backshift” operator. The actual vector of time series does not appear in this part of the equation. For positive values of  , one gets a finite-length (
, one gets a finite-length ( , actually) vector of coefficients. To get the d-th difference for the i-th element, one multiplies this vector by the vector of length
, actually) vector of coefficients. To get the d-th difference for the i-th element, one multiplies this vector by the vector of length  of the lagged time series starting at element i. For non-integer
of the lagged time series starting at element i. For non-integer  , the vectors are of infinite length but everything else remains the same. Hosking [Water Res. Res. 1984(?)] does a nice job explaining this.
, the vectors are of infinite length but everything else remains the same. Hosking [Water Res. Res. 1984(?)] does a nice job explaining this.
Hmmm … looks like further problems. I’ll remove the spaces within the tex operators, something there is making it print funny, they may be invisible non-printing characters:
#137 Phil, I think you’re confused about the algebra. The equation for fractional differencing involves the binomial expansion of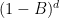 , where
, where  represents the “backshift” operator. The actual vector of time series does not appear in this part of the equation. For positive values of
represents the “backshift” operator. The actual vector of time series does not appear in this part of the equation. For positive values of 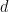 , one gets a finite-length (
, one gets a finite-length ( , actually) vector of coefficients. To get the d-th difference for the i-th element, one multiplies this vector by the vector of length
, actually) vector of coefficients. To get the d-th difference for the i-th element, one multiplies this vector by the vector of length  of the lagged time series starting at element i. For non-integer
of the lagged time series starting at element i. For non-integer 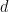 , the vectors are of infinite length but everything else remains the same. Hosking [Water Res. Res. 1984(?)] does a nice job explaining this.
, the vectors are of infinite length but everything else remains the same. Hosking [Water Res. Res. 1984(?)] does a nice job explaining this.
Hmmm …
w.
Re #140-143, Thanks for the responses TAC & Willis, I need to think about them, but got to catch a flight (without a computer) to Mexico with my wife for our 28th aniversary, and if I want to experience my 29th I had better run.
Thanks, Willis!
#129 Regarding ARMA(1,1), it might be worth noting that the ARMA(1,1) model, with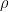 close to 1 and
close to 1 and  close to -1, can yield long time series that exhibit structures easily mistaken for long-term persistence. That is, an ARMA(1,1) can be a good approximation to FARIMA(p,d,q). Thus a physical argument for ARMA(1,1) may be simply that it provides a good approximation to the FARIMA models (which may be more easily justified).
close to -1, can yield long time series that exhibit structures easily mistaken for long-term persistence. That is, an ARMA(1,1) can be a good approximation to FARIMA(p,d,q). Thus a physical argument for ARMA(1,1) may be simply that it provides a good approximation to the FARIMA models (which may be more easily justified).
However, the debate about what statistical model to use presumes that we have either a physical basis for selecting a model or enough high-quality data to settle the issue on purely statistical grounds. I doubt either is the case. The “physics” of climate seems to be still maturing, so it is hard to know how one could provide a model that truly “corresponds” to the physics. Similarly, SteveM has convinced me that the data are not there to settle the question, either (except that we can reject the idea that climate processes are iid or AR(1)).
My sense is that either ARMA(1,1) or FARIMA models seem to do a pretty good job at fitting the data; it’s hard in some cases to tell them apart.
Having said that, however, the FARIMA models, though less tractable, have the advantage of corresponding to a rich literature on long-term persistence (LTP). There do seem to be hints of a very powerful physical explanation for LTP (though the arguments are not fully developed). Koutsoyiannis discusses this at some length.
Steve, you’ve said you didn’t want to waste time giving me tutorials. I’m not asking for them from you. I will never ask you again for a tutorial. Why are you still giving them? I just want to know what you did in your work, in your paper.
1. What were the p,d,q numbers in your ARFIMA model with which you characterized the autocorellation of the tree ring proxies. (just need three numbers: 1, .5, 1 or what have you.)
2. What were the p,d,q numbers of the generated red noise that you fed into the simulations (same values as (1))?
3. What were the coefficients (p and q, don’t bother with the binomial one) that were obtained for the tree ring autocorellation (from 1).
4. Were these same numbers used as the input red noise for your simulations?
——-
I won’t waste your time. Monosylabic answers are sufficient.
These comments are for the group (not for you, Steve). No need to read.
1. Willis, TAC: The paper that I referenced gives a very nice and tractable explanation of finite differencing, including the binomial equation.
2. It also talks about the issue of the different models well fitting existing data but giving different behaviour
3. I think one, can think about this by stepping back for a second and disconnecting the argument about what is the best model of the noise, from the issue of how that level of noise interacts with the Mannian PCA transform. Thus one can see how AR coefficient of .2, interacts, how .6 interacts, how more complicated inputs interact. then one can agree, given a certain input whjat the impact is. One can argue about what the right input is separately and can also worry about the possible implications of one of the worst ones being correct is (even if not sure that it is the relevant one.)
TCO: Thanks for the reference: I will take a look.
However, I want to point out that saying (#102)
completely misses the point. It is true that ARIMA(p,d,q) is a special case of FARIMA(p,d,q). However, the only stationary ARIMA(p,d,q) model is the trivial case d=0 (ignoring d less than 0), for which ARIMA(p,0,q) is equivalent to ARMA(p,q). However, for -0.5 .lt. d .lt. 0.5, FARIMA(p,d,q) is stationary. More specifically, for d around 0.25 or larger, FARIMA(p,d,q) exhibits structures that are remarkably similar to what one sees in real geophysical time series data.
In short, ARIMA models are both a generalization of ARMA and a special case of FARIMA models, but the only situation where ARIMA seems to be useful for climate science is where it is equivalent to ARMA.
Thanks for the expansion. Just pursuing the thought (with you, Steve can sheild his eyes): What is your interpretation (from a physical intuition standpoint) of what a fractional d value implies in terms of degrees of freedom, Aikake criteria, danger of overfitting, etc?
Maybe JohnA could move all the posts after 18 to a new thread. It is a fruitful discussion and deserves head billing, and this way the computer model talk could resume.
Remark to community (no Steve time required): I’m doing some looking at the MBH98 article and the GRL05 critique.
A. Seems like Mann’s figure 5a refers to PC’s of the hemisphere, but Steve in GRL05 (section 2) hones in on the 70 NA series to estimate autocorrelation properties. Is this appropriate or should he use the global set?
B. para 13 and Figure 2 in the GLR article, seem to unfortunately equate “conventionalness” with “centeredness” (these words are actually linked in the text and figures explicitly by parentheses) and do not clearly identify to the readers that the differences are the result of both removing off-centering AND standard deviation dividing. Are the authors taking the position that standard deviation dividing (covariance matrix) is “unconventional”. Even if they think that, they don’t lay it out and claim it. Nor does the explication explain how much of the effect is from “off-centering” as opposed to “standard deviation dividing”. I think this is unfortunate and tends to lead the reader to impression that the effect is coming all from off-centering. The Steve rejoinder that covariance matrices are conventional misses, the point: is he arguing that correlation matrices are unconventional and in any case, should he not cloud the issue by justaposing “conventional” with “off-centered”, when it is actually “conventional” with “off-centered” AND “standard deviation divided”. (We’ve discussed this issue ad nauseum and Steve and I have agreed to disagree, just pointing it out since I notice more of what he did and where the confusion comes in from his presentation, when rereading the paper and looking at those exact words of his in the para 13 and the figure.)
Para 6 of the GRL article says that Steve obtained the “complete autocorrelation properties” of the 70 series using the hosking sim program. This sounds like (1,f,1), but I will double check to make sure. If the hosking sim program, requires an input for p and q, we would need to know explicitly what Steve used. The rest of the para talks about generating 70 series for each of the 10000 simulations. The implication (although not explicitly stated) is that the generated series have the same properties as the measured red noise analysis of the 70 series. (I would be surprised, upset if this were not the case.) I also don’t get the impression that there are 70 different types of noise sereis (70 different sets of pdf correlation coefficients, and I guess 70 different f values.) Bender has suggested the possiblity of that, but if something like that done, would espect Steve to have described that exlicitly. Also it just doesn’t seemt to make sense to have that many paramaters running around. (70 times 3).
I’m off to reread Steve’s r code more slowly and also to look at the hosking.sim program.
TCO: Please quote our articles rather than paraphrasing as all too often you’re simply chasing your own tail. I realize that the Hockey Team and Huybers do not quote our articles and paraphrase them and then criticize the paraphrase. I’m getting tired of it.
In our GRL article, we described Mann’s procedure as follows:
In the GRL article, we referred to the EE article as describing the effect of this on NH reconstructions. IN respect to your concern about covariance/correlation PCs, we stated:
Wahl and Ammann obtain precisely the same results.
Just because you didn’t understand the points doesn’t mean that they were unclearly expressed. For exmaple, you’ve expressed a complete mixup about temperature PCs and tree ring PCs, which are calculated in different modules. We’ve never suggested that covariance PCs are the “right” way of doing things in the sense that they are a magic bullet. You’ said your piece on covariance-correlation matrices over and over again. If you post on it here, I end up picking spitballs off the wall and I am really bored with it. You’ve said that you think Huybers’ points on correlation-covariance are wonderful; I thought that Huybers’ points on correlation-covariance were crap. The point on RE was worthwhile responding to, but we had a complete response to it.
Ok…I’m looking at the waveslim guide right now. It is 74 pages, but the hosking.sim explanation is just one page, page 34. It is not clear to me what it does. If it determines autocorrelation properties or if it generates series. I also don’t see the pdq input or where it says what pdq it uses. there is some stuff about “freq, delta, omega”. Not sure if this is same thing as pdq or something different. Also not clear if this is an input or an output.
Also not clear to me why the reference is to the 1984 Hosking paper instead of the seminal 1981 paper on fractional differencing, but this is a side issue.
Steve, I just read, the exact part that you quoted. It was not the relevant part for me. What was the relevant part was where you said:
Were you making the argument that correlation matrixes are not conventional? And were you leading to the mistaken impression that your analyses showed the impact of centering, off-centering? Given that you changed 2 things at once, it is actually impossible to say that off-centering did anything unless you also do a test of standard deviation dividing. you have one equation and 2 unknowns if you compare 2 cases and change 2 things at the same time.
Instead of saying
you should have said
That would have been accurate.
Steve, let’s just agree to disagree on the covariance/correlation thing. I’m not getting satisfied with your defenses, but feel free to have the last word. I won’t be the one to bring it up again.
Right now, I want to concentrate on the PC1 red noise analysis.
Read #155. OK I’m glad that you’re not going to post any more on covariance or correlation PCs. You’ve said this hundreds of times; I don’t agree with your posts. I’m tired of you using bandwidth on this site to keep saying the same things over and over. You’re becoming like Peter K Anderson.
AS to the red noise, all the different persistence models do is change the spread in Figure 1 a little bit, but fractional processes are interesting and as TAC observes, very characteristic of geophysical processes. Demetris Koutsoyannis has much to say. But I’m going to have to hold you to a couple of posts a day on this as people are getting very tired of you and I’m getting a lot of complaints. I can’t spend time picking spitballs off the wall and I don’t like leaving them there. I’m not going to have the blog serve as a tutorial for you meandering through fractional processes. It’s not that there’s anything wrong with the topic; I like the topic and it’s interesting; it’s just that you’re posting too much about every little step. If you want to come back in a couple of days with your onservations, that’s fine, but not every few minutes.
Steve (on the tree versus temp PCs) I thought that you had made the point before on this blog that Mann had shown a graphic of the PC1 and described it as the dominant mode of variation (when defending your analysis of PC1 vice of reconstruction). That is why I expected you to have shown the same PC1 in your article that Mann does. Does he ever show a graphic of the tree ring PCs from North America? What gives?
I found Hosking still works at IBM. Too bad he is not an academicer. pdfs hard to find. Oh well, will check out the 81 and 84 papers in the library.
TCO – no mas. told you. If you don’t understand, I’m not helping you any further. Go read MBH98 and sort out tree ring PCs and temperature PCs. If you don’t understand it, ask him; not me. You’ve used your quota of questions for the week.
Learning about the fractional processes is an interesting sidelight, so I am cool with stopping the stream of consiousness posting on that. How about just answering the question on your method, though? I’m not asking for a tutorial, just a clear communication of what you performed in your paper.
#156
You are right that Hosking [1981] and Granger and Joyeux [1980] are often cited as seminal papers on fractional differencing. However, I like the presentation in Hosking [1984]. Also, Water Resources Research (in which Hosking [1984] appeared) published much of the early research on application of fractals to real geophysical data [e.g. early work of Mandelbrot; Wallis; Klemes; (as well as some of Koutsoyiannis)].
Steve, I would be very careful about listening to complaints or shutting me down, since you don’t have the time to deal with me (but don’t like the appearance of unrebutted criticisms). It is a very easy path to stifling debate or criticism, if you go down that road. If I’m being a moron or throwing spitballs, it should be self-evident. If it’s not, then maybe I’m making points that are at least relevant for discussion/debate. Maybe there are even some things that I have right and some things where I’m finding valid (small) faults in your work.
TCO, you’ve got to stop all the posts. Cut them back If you’ve got any concerns, you can express it in a fewer number of posts. Save up your posts and bundle them. Put them on appropriate threads. If you’re interested in Ritson coefficients, post there, not in an unrelated post.
If you don’t cut back, I’ll have to put you on hold-for-approval starting forthwith. Your posts will probably be put through eventually, but you’ll lose real-time rights if you don’t exercise some self control.
I was having a hard time understanding the hosking.sim function from the referenced R help site, so I googled it. Looks like I have some august company in my confusion:
http://tolstoy.newcastle.edu.au/R/help/06/05/26395.html
#151:
I think you are touching on an important and profound question. The short answer is I do not fully know, and I certainly would not claim to have “physical intuition”; others, including Demetris, SteveM, and a bunch of physicists (I can name a few; Lubos probably knows dozens), may have more insight. What I can say is that, for every statistic and diagnostic I have looked at, the assumption of LTP can dramatically affect one’s conclusions.
Finally, given the abundant evidence for LTP, I am surprised that this topic has not been more thoroughly explored.
This thread got seriously hijacked by Marlowe Johnson’s OT post in #18. Is it possible to perform a split at this late stage? People like Tim Ball, John Creighton et al. are very interested in the next generation of models and I think this is an important topic for detection & attribution. At the same time, the issue of tree ring autoocorrelation structure is also important, just OT. Maybe the tree ring stuff could be moved to an ARMA or Ritson thread? I have more to offer on the topic of TSA of NOAMER, after consulting today with a tree physiologist …
Re #168
Interesting. Nobody replied to his question either.
TCO, do you know offhand what package contains “hosking.sim”?
It’s package “waveslim”. Sorry for wastage.
#169. Hi, glad to see the LTP discussion. As to insight, there are top-down and bottom up ways. DK identifies a number of different process models that generate it, meaning that if observed, it doesn’t imply any particular process. He also equates LTP (or SSS as he prefers) to maximum entropy giving a nice macro physical motivation. My understanding of this is that AR(1) or any AR for that matter assumes a specific time step that is usually arbitrary. This distinct time step cannot be a solution of maximum entropy. Its like all molecules having the same identical energy — over time the distribution of energies will spread out to the ME solution.
Fractional differencing then, is really just an attempt to model the type of process that doesn’t make the arbitrary time step assumption with finite mathematics.
There is also another aspect that I would like some comment on that motivates this that is more philosphical and has parallels with special relativity. That is, in the same way SR drops the assumption of a preferred inertial frame, LTP like processes result from dropping the assumption of a preferred time frame implied by a (discrete) AR model. It makes sense that the human choice of time step should not be really relevant. That is, natural systems with LTP are like AR processes operating simultaneously at all time scales. Isn’t this the way it should be when the observer is removed?
There are lots of posts at my blog about this, simulations and plots to show AR processes do not have adequate variances at the longer time scales, whereas natural series including reconstructions show LTP, and others. Not meant to be an ad for my blog or anything, just that there is a lot of background and posts by DK that might be of interest (http://landshape.org/enm).
I really don’t know what it means for climate models. OTOH one could say that LTP implies greater long term variance and therefore potential to mistake noise for trends. OTOH one could say that the LTP is a result of various complex deterministic forcings an hence not really ‘noise’ in the sense most people understand it.
I’m not sure what all the fuss about fractional differencing is here. For continuous processes (like streamflow, say) it might make sense. But to the extent that trees are temperate organisms with annual life cycles, I don’t see the application there.
#174. In looking at temperatures reconstruced from tree ring proxies the minimum time step would be annual. That is, it is not a binomial sum of averages less than a year. But if the temperature measurements are more frequent, and of course temperatures are actually continuous, the steps are different.
Re #175
*I* realize that. I am just hoping the effort being expended on fractional differencing is not being driven solely by the Marlowe Johnson inquiry on tree rings.
Re #168
TCO, I just checked the R implementation of hosking.sim. It is, unfortunately, not going to tell you the answer to your question. At least not directly. This is because R is making an external call to some custom C code “hosking.sim” that is not accessible for viewing from R:
> hosking.sim
function (n, acvs)
{
.C(“hosking”, tseries = rnorm(n), as.integer(n), as.double(acvs[1:n]),
PACKAGE = “waveslim”)$tseries
}
To completely understand what that function is doing you need to see the source code. This is not a final answer to your question. Just an update. I may investigate further if I get the time. (Thanks for looking up the code and reporting back.)
#176. OK. Am somewhat late to this party. I would think that in general series with LTP provide better representation of natural series and if used in a monte carlo way would generally be ‘worse’ than AR or ARMA in generating apparent trends, depending on the specific parameters though. So LTP shouldn’t help Marlowe Johnson argument at all. I was responding to #169. I would rather talk about next generation models and the split as you suggest in #170 sounds good.
Got the hosking.sim C source code from the waveslim tar source file stored at CRAN. Looking it over …
TCO, you never answered #124.
I believe I have the answer to your question. I believe it is what I said way back in #71. I would have to run a bunch of tests to be sure though.
Re #179 (2)
This means we can close this discussion, move it somewhere else, and get back to “next generation models” – which many want to hear discussed.
#178
IMHO, the fracdiff package, also available at CRAN, does a nice job both generating and fitting FARIMA models. It is also well documented.
By the way, for those who don’t know “what all the fuss about fractional differencing” (#174), I would recommend sitting down in front of a computer and generating a few hundred 1000-year realizations from some iid, AR(1), ARMA, and FARIMA(0,d,0) models. These are all special cases of FARIMA models, and can be generated with fracdiff.sim, using parameters![(\rho,d,\theta)=(0,0,0)[/theta];](https://s0.wp.com/latex.php?latex=%28%5Crho%2Cd%2C%5Ctheta%29%3D%280%2C0%2C0%29%5B%2Ftheta%5D%3B+&bg=ffffff&fg=000&s=0&c=20201002) latex (\rho,d,\theta)=(.9,0,0)[/theta];
latex (\rho,d,\theta)=(.9,0,0)[/theta];  latex (\rho,d,\theta)=(0,.4,0) $.
latex (\rho,d,\theta)=(0,.4,0) $.
Also compute your favorite time-series statistis for each realization: PACF, trend (assuming iid; for AR(1), etc.); mean, variance, etc. Most important: Plot the data!
You might also want to remind yourself of what real geophysical data looks like. Go back in ClimateAudit and look at all of SteveM’s time-series plots (even, maybe particularly, the proxy data). Note the structures that appear in the records, whether they are 100-years long or 1 million years long.
You will be amazed. It’s hard not to wonder what is going on here.
bender, thanks for looking at the source code. I couldn’t figure out how to download it. I got the guide, but not the actual code. I suspect (but don’t know) that even looking at the code in detail, that we will still have some input (maybe p limits) that Steve would have hard coded in as well and that are not automatic. This would all be easier if we knew what Steve had done (in detailed description of method, not on math theory).
I guess the other possibility is that the sim just takes one series, abstracts it’s non-iid behavior, then creates a noise sim based on that. Without ever telling you what you found in the original series. In that case, you might have 70 different types of series as you had speculated. I would worry about such a plan, since there would be a huge amount of parameters and since it is relevant to understanding to know what kind of model was fitted (reference the paper that I showed which describes how ARFIMA and ARMA models may be confounded, how ARFIMA fitting does not nescessarily converge to ARMA solutions as special cases, even when it should.)
If we move the discussion, would ask that these posts be moved, if that is not too much trouble (or the computer posts be moved since there are about 17 of them).
Bender: I just want to nail down exactly what Steve did. Discussing the impact of alternates and the appropriateness of his choice is a different issue, that has been teed up as well. But let’s get the simple facts on the table. There is no reason to have to debate or wonder exactly what procedure was done.
Google (on waveslim and hosking.cim) led me to Huybers’s SI for his comment on Steve’s GR letter. I could not find any explication of how hosking function works, but there are some Huyber’s commments annotating Steve’s R code–maybe bender or Stockwell can find something in here that is useful.
ftp://ftp.agu.org/apend/gl/2005GL023395/
I downloaded the waveslim package, but could not run it without R. I tried viewing it in wordpad (was hoping for some readmes, comments) but did not see much. The online waveslim guide at r-cran with the hosking.sim explanation is very sketchy…as Gene Wahl mentioned.
I’ve figured out that the author of waveslim is whitcher (UK scientist at Glaxo). Will send him an email for explanation of hosking.sim function.
Dr. Whitcher:
Apologies in advance if this question is not poorly worded–I am not a statistician or an R user. I do understand at a crude level ARMA, ARIMA, and ARFIMA.
I am trying to understand what the hosking.sim function does in the context of understanding a researcher’s description of some work he did.
A. Is it correct to say that hosking.sim “does ARFIMA”?
B. Does hosking.sim “measure” the autocorrelation properties (p,d,q) of a series or set of series? Spitting out what the correlation coefficients should be? Or even what the p,d,q order should be?
C. Does the sim create new series (with specific noise properties)?
D. Does it somehow make new noise series based off of old series without ever displaying what the old series properties were? (both A and B and not showing the intermediate?)
E. When using the simulator, does one have to specify an order? As for instance an ARMA (2,1) is different from an ARMA (1,1) from a ((1,0)?
F. I assume that the middle “d” fractional number is solved for?
Thanks in advance for any assistance.
What hosking.sim() does is generate random simulations of a process that has a certain autocovariance structure. The autocovariance structure is passed to the function hosking.sim() as one of its parameters. So what hosking.sim() “does” really depends on what is passed to it. Thus the information you seek is not in the hosking code, or part of R. It is wherever the call is made where stuff gets passed to hosking.sim(). The question is what is that “stuff”. Presumably Steve or Ross have a script that contains all the high-level code that is their analysis. It’s in that script where you’ll see what exactly is being passed to hosking.sim. Look for the call, look at what the third parameter is that’s being passed to it, and work backward from there. I suspect that what is being passed is the autocovariance function of the 70 NOAMER series. Then the only question is how exactly are these autocovariance functions being estimated. My guess, as I said very early on, is that it is effectively an AR(p) model that is being used. But the details matter if you are really insisting on an exact desription of what was done.
Your questions in #185 are not well-posed and too context-specific. I doubt you would get a coherent reply. I doubt you’d get any reply.
Finally, it is still not clear to me why you are obsessed with what is a trivial detail. This is a lot of secretarial work with no apparent benefit.
188. Good points. I am thinking along similar lines. Do you think that the Rscript file in Steve’s SI has the adequate information to answer this question? Here is the relevant part, I think:
blog cuts it off let me try again:
#arfima version (used here)
if (method2==”arfima”) {N LESSTHENSIGN -nrow(tree);
b LESSTHENSIGN -array (rep(NA,N*n), dim=c(N,n) )
for (k in 1:n) {
b[,k] LESSTHENSIGN -hosking.sim(N,Data[,k])
}#k
}#arfima
The M&M script referred to in #186 is – surprise, sursprise – exactly where they say it is in the GRL section 2 footnote 1, namely:
ftp://ftp.agu.org/apend/gl/2004GL021750/2004GL021750-script.final.txt
And the call to hosking.sim() is in section:
#SIMULATE RED/WHITE NOISE
subsection:
#arfima version (used here)
I do not post the whole code because it contains the dreaded ASSIGN operator,
But the critical call to hosking’s arfima is here:
hosking.sim(N,Data[,k])
where the acv (named Data[,k]) passed to it is calculated earlier on:
Data[,k] ASSIGN acf(tree[,k][!is.na(tree[,k])],N)[[1]][1:N]
Which is exactly as I posited in #71: the order of the process is p, where p varies among chronologies. In other words he uses ARIMA(p,0,0) or, shorter, AR(p).
Ergo Steve’s description in the GRL paper is 100% accurate.
TAC: Thanks for the comments on fracdif. Just out of curiosity, how does one enter coefficients for higher order processes p=2 for example? I always have to keep track of the difference between the number that is the order and the number that is the coefficient. Not sure if there is such an issue with “d” or if the fractional difference is both the order and the coefficient?
For others: Here is a cool page with lots of stats publications with Whitcher: http://www.image.ucar.edu/staff/whitcher/papers/
Bender: ‘
1. I’ve already been looking at it (since last night). See blog comments. I told you I was in the SI….
Thank you for that interpretation. How can you tell that it is a p,0,0 process and if so, why would steve make the point that it is ARFIMA if the d is held at 0?
The last bolded line in #189 indicates that the acf is being passed to hosking. The acf is of whatever order is required to explain the entire autocorrelation structure of each tree ring series k. (I call it “order p” to indicate it varies.)
You’ll have to ask him. I thiink he was trying to give a generalized description of the algorithm as opposed to a specific description of what he did with the algorithm.
Important to realize that hosking was a convenient choice not because of potential for fractional differencing, but because it has another beneficial property, which is that it simulates on the basis of the whole acf, whatever order it happens to be. That means that the generated series are very realistic. If instead you used ar(1) then a critic might complain that that’s artificial & overly simplistic. Using ar(p) takes away that argument. Sometimes you have to do things like that because reviewers can be thick and sometimes need to be placated that way.
Am doing some reading on acv (seems to be a different concept than ARIMA pdq stuff).
http://www.qmw.ac.uk/~ugte133/courses/tseries/8idntify.pdf
http://www.xycoon.com/basics.htm
Re #193 This line of questioning is truly a waste of your time. Real-time reporting of your reading activities is a waste of bandwidth. Your question has been answered. There is no need for further questioning. Last post on the topic. For the benefit of CA readership, please make it yours as well.
My question is certainly not answered. You had a blithe remark, but have been wrong in the past. In addition, the explanation does not gibe with certain other things, like Steve’s remark that fractional differencing was used and that I needed to read Hoskings 1984.
Maybe it is a waste of my time, but that’s my deal. I do appreciate your involvement, but if it is too tedious for you and you leave the thread, I’ll understand.
#190 TCO:
I am away from my computer, so I can’t check the following but I think it’s correct. Also, I am not certain I understand your question, but I will try to answer what I think you are asking.
OK. I typically use R, and employ the fracdiff package if fractional differencing is involved and the arima command (part of the R system that gets loaded at startup) if it’s not.
Usually, if you are fitting a stochastic process to data, you specify the order of the model in (p,d,q) format, where p, d, and q are small integers. In arima, d refers to the number of times the series is differenced before the ARMA model is fit; in fracdiff, d is a coefficient that must be fitted simultaneously with the ARMA model (thus one does not specify d in the case of fractional differencing; its value is returned as part of the result). A typical command might look like arima(yourdata,order=c(2,0,1)) (this corresponds to an ARMA(2,1)). If you want to employ fractional differencing, say with fracdiff, the command is written fracdiff(yourdata,ar=2,ma=1). The result in either case is an R object that includes the fitted coefficient values corresponding to the model you have specified.
There are also commands to simulate random realizations from a specified model. In this case, you must specify the coefficients (the length of each coefficient vector implicitly indicates the order). For example, fracdiff.sim(100,ar=0.3,ma=0.1,d=.2), would generate a random series of length 100 from a FARIMA(1,1,1) model; I don’t recall if fracdiff lets one specify a vector of coefficients — you may be limited by the software to p .le. 1 (there is no theoretical reason for this limit). The corresponding arima.sim command for an ARMA(2,1) might be: arima.sim(n = 100, list(ar=c(0.3, 0.2), ma=c(0.1))).
Does this address the question you were asking?
Yes, thanks, much. BTW, do you understand what order and coefficients that Steve used for the red noise in his GRL article? Steve is unwilling to anser direct questions and has pushed me off trying to figure it out from the code and from articles. I have tried reading the code, but don’t understand all the terms.
TCO – Our GRL article stated the following:
This is a complete description of how the pseudo-network was calculated. Not only is the code a reference, but it is actually usable, as Huybers, Wegman and others have confirmed. If the Team provided this sort of information, there would be no need for inquiries. Your allegations that the methodology was withheld and that you are prying it out of me are false and very objectionable. I’m sure that acolytes of the Team read your comments and draw incorrect conclusions.
Re #197 The question was answered. The order of model varies among chronologies. The proof is provided in #189, explained in #192, and this was my initial guess in #71. If you would like a second opinion, that’s fine with me. Make sure you point your second expert to my posts to save them some time.
I know I said #194 was my last post. But Steve’s point in #198 is spot on. The methods were not witheld or misdescribed, and your pretense that they were, then and now, is objectionable. You clearly do not undersand what acf is doing in building Data[,k]. I suggest you read the documentation for acf, and try a few examples. But to do that you need to install R, which you haven’t done. You can not conduct an audit without an auditing toolkit.
I have a feeling this is not my last post, but I wish it were. Keep playing dumb like this and you are going to get kicked off for bandwidth wasteage. Good luck installing R and trying some examples. It’s easy and worthwhile.
200. Thanks Steve. I’m not (nor have I) accused you of withholdiong information. I’m trying to figure out if all the needed info is in there. Once I know that, I will make an assertion as to completeness or lack of things. Right now, I’m just trying to translate from the code and such to coefficients and orders in ARFIMA terms. (Don’t bother teaching though…I released you from tutorials. Bender and I can noodle it over.)
P.s. Please don’t worry so much about the Team misconstruing things. Just be phlegmatic.
201. I appreciate your posts and work together as a team with me, to understand things. You may very well have it right. I just need to make sure. Will direct the second expert to your posts and do some studying of the basic concepts as well (don’t want to irk you anymore with concept explanation.)
Re #195
Everyone makes mistakes, so that is a meaningless statement. To determine if soemone’s argument is correct, you look at their argument, not whether they’ve ever made a mistake. And I’ve not been wrong anywhere, although that’s twice now you’ve falsely accused me of this. This habit of yours of false accusations is going to get you suspended. I’m keeping track of these false accusations, you know. So be careful.
I believe I explained that one. Steve said in #73 he used “an arfima model”. Which he did. You are misquoting what he said, misunderstanding what he did, and accusing us both of being in the wrong. It is you who is wrong. Keep it up.
Re #201
I appreciate the revised attitude. The answer lies in the acf() function. You need to understand that last bolded line in #189.
Only slightly OT, but Pielke Jr. has a pretty funny link related to weather forcasting and models at his site here.
Apologies if someone already pointed this out!
Steve, I have emails in to Wegman and Huybers to ask about their replication of the red noise simulation (waveslim code) for section 2 of the GR letter (stuff you just quoted). I’m sure you’re right that they did replicate it and it was obvious to a trained worker what was being done. I will just check…
Dr/1LT Huybers and Prof Wegman:
1. Do you understand what type of red noise (AR1=0.9? or ARFIMA=??? and same for all 70 series or varying?) Steve McIntyre uses in his GRL article (where he feeds 10,000 different sets of 70 red noise series into the Mannian transform and gets a PC1)?
2. Could you explain it to a layman like me?
3. Did you explicitly replicate this part of Steve’s work (using the waveslim hosking.sim plugin for R)?
Have been discussing it on this thread at Steve’s blog (discussion starting at post 18, sorry for the wandering nature): http://www.climateaudit.org/?p=836
TCO: #199 states:
If that last statement is true, it comes as a surprise to me and you really need to remedy it. R is easy to use, and you will learn an immense amount about climate-related statistical issues by, well, playing around with both real and simulated data in R.
Bender, SteveM, Wegman and others may be able to answer your questions, but in the interest of everyone’s productivity and sense of well-being, please set some time aside and learn R. For all of us.
I’m downloading it now against my better judgement. I think that having me read Hosking articles and look at SIs and download R and such is actually more laborious for all concerned (including Steve and I). Steve could have said in a paragraph what Bender disclosed (if Bender has it right, still not clear on that.)
Re #208
I appreciate your diligence TCO, but there is an important point of principle here. In an Open Audit world there should be no need for you (or anyone) to question Steve (or any author) directly. You download his script, you run it, you replicate his results … or fail to. If you fail to replicate, *that’s* when you start writing the author. It’s bozo simple, and the idea is that anyone can do it. If Steve is spending his time answering your questions directly it sort of defeats the whole principle of having publicly available scripts that run on GNU licensed software.
Congratulations on deciding to download R. Once you are running these scripts it will make it alot easier to understand what various authors are doing. The graphic in #87, for example, takes only 15 lines of code. But it tells you so much about the behavior of the NOAMER proxies.
When you ask Wegman if he “replicated” Steve’s work, recognize that “replication” is subject to interpretation. Wegman used AR(1) models. Steve has done many different flavors of ARFIMA (including white noise, red noise, and persistent noise), although the GRL article reports on the one batch that were done by feeding acf’s to hosking. (I would call this persistent red noise because the models are AR(p) where p ~ 6.) Bottom line: the signal-mining effect of Mannian regression is so strong that any flavor of null modeling is going to produce the same result.
Well that will be a nice surprise for them.
#208 Excellent decision! You clearly have a lot of energy for this topic, and a lot more to contribute. This is the right path.
I also want to respond to your comment that
Well, you may be right. But Hosking is a truly great mathematical statistician and a gifted writer (full disclosure: I know him personally). Your time will not be wasted. In fact, once you open up one of his articles, you are going to want to read everything he has ever written, on topics from L-Moments to determining bias from expectations of third partial derivatives of likelihood functions. Pure magic!
Forget about climate for a while and just learn this material. It is not easy; but it is immensely rewarding.
Good Luck!
Fig. 1. This graphic indicates why a persistent noise moel is a good choice for the NOAMER tree-ring series. Note especially in (a) how the order of the ACF is ~p = 8.
(a) Mean of the 70 NOAMER tree-ring series
(b) acf of the 70 NOAMER tree-ring series
(c) pacf of the 70 NOAMER tree-ring series
(d) smoothed spectrum (see how red it is?)
Fig. 2. This graphic represents the average PACF mesaured on each of the 70 NOAMER series. Note the pacf is ~ p = 6. What’s good for the continent is good for the region: these series are all high-order persistent.
TCO’s homework is to recreate these figures. The reason they’re relevant is that they show the approximate order of the acfs being passed to hosking.sim().
Speaking of Hosking, I ran across a 1980 monograph (“Applied Modeling of Hydrologic Time Series” by Sals, Delleur, Yevjevich & Lane) that ties together two separate issues – (1) physical interpretation of the ARMA model, (2) ergodicity & sampling error – all in 2 pages.
On p. 8 they provide a nice diagram of the hydrological cycle explaining why streamflow conforms well to the ARMA(1,1) formulation.
On p. 9 they describe the importance of “infinite universes” in time-series forecasting. Of particular interest to the doubting TCO:
“The values observed in the historical series of any given number of years is only one realization of the infinite number of possible realizations that may have occurred during that time. Consequently the statistical chractersitics derived (estimated) from that sample are only one possible estimate out of many others. That is, the sample estimates are random variables and so they are uncertain. Whenever possible and necessary, such uncertainty must be incorporated in the modeling of hydrologic time-series.”
They go on to make the helpful distinction between an estimate of mean, or variance, from a single realized time series – which, being based on many observations, is not very uncertain – vs. an estimate of autocorrelation structure, which, being effectively based on only a single sample, is highly uncertain. (In the case of forecasting the desired scope of inference is larger than just the population represented by the years sampled; it includes all possible outcomes that could be realized in coming years.)
Hadn’t quite thought of it that way, but that is exactly the problem: it takes a lot of data for a sample autocorrelation function to converge on the true ACF of the population/ensemble. (In the case of 1/f noise, you don’t even get covergence!)
TAC:
In all seriousness, I’m not a statistician or mathematician of any sort. Just a dude who surfs the net. I hated that part of calculus or algebra where they made us learn about the determinant of a 3 by 3 matrix. I never used it. I think pushing me to learn R, etc. is not a useful use of anyone’s time and is maybe a bit of an evasion, rather then a requirement to answer questions.
My basic question revolved around what Steve did. There was an argument that he should use AR1=0.2 instead of AR1=0.9. Independant of what red noise structure is most appropriate* for testing the mining behavior is the basic question of what did Steve do? To me, it’s like separating the question of what did Karl Rove say to a reporter (or what Bill Clinton did to Monica) from the issue of whether it was right to do so. One issue is a simple issue of fact. The other is debatable. When someone is asked a question of fact and tries to avoid answering it, by shifting to the (unstated, but anticipated debate of significance) that is shifty. Comments on what one could do (in terms of running other tests to look at the bias) are also jumping the gun. Worthy in general, but non-responsive and shifting from the direct question on the methods performed.
I think a paragraph or sentence long characterization would have been sufficient. If the answer were** “we used AR(p) with variable rank and coefficients for the 70 series”, then I could have easily googled definitions or gotten bender to explain it to me.
P.s. I have had some preliminary conversations with Hosking and Huybers.
*I think the issue of which series is selected is an interesting one as well. The 70 NORAM series would seem to have a proclivity for higher trends (or autocorrelation) then the overall set of series. Looking at the biggest challenge is probably useful in terms of showing off the bias (which exists to some extent regardless), but may not be the fairest choice if the reader gets the wrong impression that the overall data set suffers to this extent. This can be solved by simple disclosure in the text by Steve to explain why he chose that set of records. That’s the fair thing to do.
**For Bender eyes: It’s still not clear to me that this is the right answer;
1. Steve is mum.
2. I am not clear what an acf or acv function is (in general or in this program)
3. Nor do I know how to read the syntax to see if 70 different rednessess are created or if there is one created and then 70 runs of it are done (varying by chance).
4. Also, still not clear what part of the syntax says that this is an AR(p) process.
5. Or how AR(p) equals fractional differencing.
6. The other concern I have (I expressed it before) is that if we have 70 different “types of redness”, that is a LOT of paramaters. I don’t at all assert, but would wonder if we could fit an elephant with that. Wonder how much the derived simulated proxies would differ from the dataset. Your recent post fits into this. I feel better taking 70 series of similar physical nature and getting one description of them overall then getting 70 different versions…I was “intuiting” this earlier.
If you are concerned about bad apples, come up with a (stated) defintion of the bad apple and show how the algorithm performs with/without bad apples, with percent bad apples, with “badness” of the apple. This is just basic thinking process. The sort of thing that you would do if you were investigating a phenomenon in a factory or such. What BC would do. STeve does this in a sense with his “dotcom” examples or single bcp tests, but the examples are so singular and so much chosen for effect rather then for learning, that it is not very helpful. graph the darn response surface. Show where things are especially bad, show where they don’t change that much. Be phlegmatic and honest and curious and don’t just do stuff to try to win points against an opponent rather then exploring an issue.
Re #214
1 no comment
2 keep web surfing, you’ll get it (correl = cov/var)
3 k goes from 1 to 70 across the “tree” data matrix; each time thru the loop, an acf is calculated and passed to hosking.sim
4 it is not explicit in the syntax; it is implicit in that you are passing the whole acf, however many coeffs are in that; probably 25, but probably only ~6 of which are 95% significant; running the code would tell you
5 it doesn’t; using hosking.sim as ARFIMA implementation conflates two issues
6 it’s the tradeoff between realism and parsimony; had he done it more parsimoniously someone would have complained the noise series weren’t representative; could he have done both? yes, but it would have made for a longer paper.
Most of this I’ve explained already. Maybe expressing it differently a seecond time helps?
Re #216
A follow up. The graphics in #212 might help answer q. in #214, but they are not showing.
#214 TCO,
I apologize if I inadvertently reminded you of bad math classes. I am well aware that math is often taught so poorly that people come away hating it. This is a shame, because math is both inherently beautiful and empowering.
I also want to assure you that my recommendation that you develop some skill with R is not at all “a bit of an evasion.” To the contrary. Having R under your command will help to sharpen your insights, make more pointed arguments, and deliver deeper criticism.
I have to go now, but I am not done.
216. Yes.
218: you’re a cool guy and it did not come accross as an evasion from you. some comments from others have. Did not mean it from you.
*Just musing here: you know given that (all, most?) of the bcp series have a hockeystick shape in same direction or some consistent physical subset of them do (strip-barkers), I think it is wrong to think of those long blades as noise. What are the odds that all those series could happen by chance? It is a signal of some sort. So, the implication ought to be that the Mannian transform magnifies a certain type of signal, a certain type of SHAPE, not that it magnifies autocorrelation.
Re #221
You’ve been talking to someone. Good!
“Noise” and “signal” are relative terms. Let’s agree with your view that the bcp 20th c. blades are not “noise”; they’re “signal”. The problem is that the “signal” they represent is NOT a pure climatic signal – which is what we’re supposed to be reconstructing. The blade is too steep (just compare strip- vs. full-bark). My guess is that this represents a hypersensitized response to climate, so that part of the blade is climate signal, but part of it is a spurious result of a non-climatic amplifier of climatic signal. Viewed that way, it becomes a matter of semantics whether you want to call the steepness of this blade “singal” or “noise”. The point is: if it is signal, it ain’t usable signal. May as well call it persistent noise, then.
the bcps could be non-climatic or they could be the only useful ones or they could be intermediate. But the fundamental thing is that the transform mines for shapes. If you had 10 thermometers and 90 pendulums, and the climate rose and affected the thermometers, the transform would magnify the effect of the thermometers. (and actually the ideal transform would be to get rid of the pendulums and keep the thermoters. You can come up with several other different types of thought experiments. Still, I really do think you can deconvolute the method versus the input. the method doesn’t know if the signal is climactic or not.
?!?
#220. Now you’re hopefully starting to understand the issue that was discussed with von Storch and will start to understand some of my comments instead of screeching about not understanding them. Take a look at the slide that I presented on this in my Stockholm PPT and you’ll understand the effect better. The Mannian method is strongly data mining, but its impact in a practical setting is better illustrated by the effect of a couple of nonclimatic HS series on a pseudoproxy network with an actual non-HS signal than the red noise networks of our articles. That doesn’t mean that the statements in the article were incorrect – they weren’t. Just that the VZ exchange cast light on the matter. VZ used the word “steering” in their article and that’s a word that I like.
#221
TCO: You have brought up a very important point, I think. In most fields (though apparently not climate science), there are well established statistical models. (As SteveM notes, in financial matters the accounting/statistical rules are particularly carefully defined). The role of the statistician is somewhat trivial in such cases; she simply calculates the projection of the high-dimensional data onto the low-dimensional subspace (the “model”). This can only be done correctly in one way; it always yields the same “answer”.
However, if a scientific field has not matured to the point where it has established models (chosen either because of physical arguments or by examination of many long datasets), then one might resort to a “default” “white noise” linear model. However, this is not mandated (or if it is, it is seldom enforced). If one can get away with it, it is temptiing to invent a custom model for the specific dataset at hand — bad practice, sure, but only a few people like SteveM see what’s happening.
The point is that by choosing the shape of the subspace onto which one condenses the data, it is possible to ensure almost any particular result one wants. For example, from what I understand the method in MBH98 preferentially produces hockey sticks (LOESS smooths also tend to produce hockey sticks, but to a smaller degree).
Many people, including some scientists, assume that statistical methods do little more than extract the signal from the data. This is what introductory statistics classes teach. However, it is simply not true when dealing with sophisticated methods. When using such statistical methods, one has to be very careful that a strong signal — a trend, for example, or some other salient property — is an artifact of the data and not of the fitting procedure or model.
As you note, another difficulty involves defining what data are “good enough” to be used, or “bad enough” to be excluded. Biased samples yield biased results — no surprise there.
One last point: If one is dealing with geophysical data, I would argue (see Koutsoyiannis’s work) that the “default” model ought to include long-term persistence. Hurst pointed this out in 1951, and although Hurst’s work is still debated, it has never been discredited.
Re #223
Dude, what if a subset of your pendulums are responding to temperature somewhat like a thermometer, but not exactly with the same degree of sensitivity as a thermometer?
That the problem with the strip bark bcps: the temperature response (if that is what it is) is exaggerated by something else that we don’t understand yet. That’s why the persistent noise models make the point: they allow you to simulate spurious effets that *look* like signals but are in fact something else. (If we know what that was we could call it a signal of that. Since we don’t, we must call it something else. Non-climatic signal. Persistent noise. It doesn’t matter what you call it. The point is Mannian methods will mine for shapes like that. Put in HS temperature data on one side, a mess of persistent noise series over on the other, and you’ll pull out an HS-shaped spurios “signal”.)
I don’t want to sound pessimistic but I’m not sure you will ever really understand this unless you get to the point where you’re running these scripts for yourself and seeing with your own eyes what these methods do. You will just keep asking the same questions over and over again, coming at it from different angles each time, but never seeing the core of the problem. Hopefully not, but …
227. Let’s keep it on the subject, not on me. wrt your “what if”, I agree that there are many other “what ifs” that one can make. The key issue to me (and I think you) is to consider how different situations interact with different methodologies.
221:
“all those series??” No, only the CA trees. You just don’t get it, do you? You can’t let the outliers dictate your conclusions, without some real good reason.
Steve:
I think that I understand (and understood) the issue with VS which has to do with the type of series used to test the method. The method mines for certain types of series more then others, so that more extreme examples show this effect of concentration/mining more.
I’m concerned about your use of the term “nonclimatic” with respect to the mining (in this post and in the presentation). Suggest instead using the term “not nescessarily climatic” or just avoid the issue in general. The fundamental idea is that the method mines for certain shapes. It would do this whether the shape was the instrumental Jones derived NH temp series or whether it was sheep-de-grazed bcps.
Also suggest intstead of focusing on what is a good example for showing the effect to extreme, to just investigage in general what sort of mining the transform does, how the input effects that etc. Learning how something works and to what extent it does is more important then showing examples for effect. If you do decide to show examples for effect (and pick more extreme ones then typical of the overal data set), it is important to say in text that the example is for effect and may be more extreme then expected in practice.
Small nit, am concerned to see your use of the term Mannomatic on these slides and in your GRL SI as analagous with the Mannian transform derirved “PC1”. At other times on this blog, you have used the term to mean the overall reconstruction method for Mann.
Small caveat, I could not find your stockhold presentation, looked at the Holland one, which you indicnated was similar.
In the illustration with von Storch pseudoproxies, the network was climatic but did not have an uptrend in the section selected. A nonclimatic HS was inserted into the network. The Mann method mined for the HS series though it was nonclimatic by the construction of the network. I think that the term Mannomatic has usually been used for the PC method, but I could have occasional variant usage. To my knowledge, it is not yet a recognized technical term.
Yeah, you seem to have a habit of that, but also used the term differently…it was in context of a discussion about reconstruction versus PC1. Reason it pricks my ear, is the habit of muddying the differentiation.
Rest of 231: 230 applies.
Re #230
Has he? Where?
#212 again, for TCO
Fig. 1. TSA of 70 NOAMER tree-ring series; (a) Mean, (b) acf, ( c) pacf, (d) smoothed spectrum.
Fig. 2. Average PACF mesaured on each of the 70 NOAMER series.
#212 again, for TCO (with trailing white space this time)
Fig. 1. TSA of 70 NOAMER tree-ring series; (a) Mean, (b) acf, (c) pacf, (d) smoothed spectrum.
Fig. 2. Average PACF measured on each of the 70 NOAMER series.
bender: I will reply. May be a few days as I am pretty fried. want to give this some thought. (May have some light posts elsewhere in mean time.)
Bender:
On your graphs: Not immediately clear what graph corresponds to what in terms of the “what did Steve do in GRL” waveslim discussion. Please let me know if you want me to ask questions or to go web study this stuff first.
Re #237
These graphs show that the NOAMER series are roughly AR(6). i.e. If you pass the entire acf to hosking.sim() as in Steve M’s code, and as in the GRL paper, it’s only the first 6 lags that contribute anything toward the tendency for red noise to produce low-frequency false signals. This supports my contention that he effectively used an AR(p) model with p variable among the 70 chronologies but averaging around 6. (I could put error bars on the second graph and that would tell you how variable the p is.)
Please reply as to if you want me to ask specific questions.
No, I’m good, thanks.
From help(acf):
lag.max: maximum number of lags at which to calculate the acf. Default is 10*log10(N/m) where N is the number of observations and m the number of series.
The length of the acf therefore defaults to 28 (n=581), 6 of which on average tend to exceed the 95% significance threshold in the NOAMER dataset.
That fully answers the original question.
Re #213
Steve M you may want to check out the last couple of lines here. I think I may have figured out a major problem in autocorrelation analysis in dendrochronology that stems way back to Fritts (1976). I don’t think these guys understand the sample statistic convergence problem, and so that’s why their AR (& ARMA) models don’t work so well (all that nonstationarity, not just in the mean and variance, but the sample acf too!). Maybe Jean S will want to contemplate this. (If I’m right it will give you an edge in future modeling efforts.)
Re #242
This helps explain our different experiences with ARMA models on tree-ring data as well (can’t remmber the thread; one of the ARMA ones): I always work with detrended data, never HS-like. Aha …
I can’t help myself. These are the things I’m wondering, right now. No requirement to respond, bender:
From bender #141 (kudos on looking up maxlag btw)
1. The noise simulation is ARFIMA (28,0,0)= AR28?
2. Do we still think that there are 70 different types of red noise? The definition of max lags includes the number of series, so it seems that we are considering the overall data set (all 70 series) not making a different red noise model for each one. I guess you could have different structure for each one (in coefficient, but not in order). Anyhow, this area still seems unclear.
3. My reading on acf and acv says that sometimes the terms are used interchangeably, sometimes they have different mathematical definitions. I wonder if the “acvs” that hosking.sim asks for is the same quantity as what that “acf” of R spits out. This is an issue of precise mathematical definition.
Fractional differentiation:
1. Still not clear to me why Steve referred me to fractional differentiation as a stopper to understanding what his noise structure is. Seems that just saying it’s AR28 would be simple if that’s what it is. And he didn’t just use the term ARFIMA. He actually told me to read Hoskings and said that ‘fractional differencing was hard even for him’. Either we are still missing something or Steve was misleading.
GRL article:
1. I wonder what the graphic on the HS experiment would like with correlation matrix run as the comparison. (i.e. just looking at off-centering as an issue, not muddling in standard deviation dividing). Is the resultant centered or bimodal? Closer together for the two humps?
2. I wonder why the results are shown in a histogram instead of a distribution curve. There were 10,000 runs. Wonder what the curve looks like.
The more I think about this, the more I think that Steve’s results overdramatize the problem. Sure, for a 70 seperate AR28, non-detrended (but had trends) acf-determined set of coefficients, one gets the result that he showed. It is intriguing to me that Wegman used an AR2 challenge instead. Of course, there is still a bias regardless. I just think it unfortunanate when Steve does things that overdramatize it and does not straightforwardly say that he is doing so, for effect. I mean the covariance versus correlation, this AR28, Preisendorfer’s n, etc. All the choices lead to overdramatizing the impact of the “cadillac criticism” of off-centering and he muddles issues to allow it to look like “off-centering” is carrying the load that several factors do. It reminds me of dealing with investment bankers. They won’t lie to you. But they won’t tell you the story straight, won’t point out places where the deal is skewed.
This part is just bizarre. Is the matrix supposed to be able to tell if something is non-climatic? And what does it mean to be “climatic” or “nonclimatic”? Surely the matrix just crunches math. If we had a “climatic” HS (say instrumental temp) and we had a bunch of nonclimatic series (say pendulum swings), then the network would select the climatic and leave out the non-climatic. It’s IRRELEVANT, the climaticness (if that is even a word) in terms of evaluating how the network functions.
I also find Steve’s running to say that Wegman and others have shown the bias or that one can see it with a simple AR1 model to be a bit off-putting. It’s like he wants to shift the discussion from what his red noise model was. Like he doesn’t like the scrutiny. I have no doubt that the bias can be shown with other methods. But when someone tries to shift examination from himself to another, it makes me wonder if there is some fault in the former. Whether or not the bias exists in general, would not change the issue of whether Steve’s red noise was properly modeled. For one thing, Steve may have overdramatized the effect. It’s annoying that every time there is a judgment call, it’s not clearly pointed out and I MEAN BUTT-CLEARLY, not a 10K Enron footnote type caveat. And every time the judgement call seems to go in the direction of overdramatizing off-centering.
Typo: Wegman uses AR1=0.2. At least he does in Fig 4.4. It is not explicitly stated what type of red noise he uses in 4.2, in the figure which is the analog of Steve’s red noise/HS figure from GRL.
Wegman notes on Figure 4.2 that his result is not indentical to Steve’s Figure 2 in GRL, but shows similar features. I would like to know what is different between the two and why. Eyeballing the figures, they look very similar.
Also, I’d like to know if Wegman actually duplicated what Steve did (with the 70 different AR28 series per Bender) or if he did something simpler. I find Steve to be a bit Clintonian (equivocating) on things like this. He will say he didn’t have sex, but won’t answer questions on the definition of sex. I want to know if Wegman duplicated the whole shebang (hoskings.sim and all).
looking at the definitions in waveslim, hoskings.sim asks for the “autocovariance sequence” or acvs. It is not clear to me that this is the same thing as the “acf” that R calculates. Not clear if it is the right argument to be passed over.
TCO, I have nothing to add to your conversation except to point out that’s 7 posts without a reply. At what point do we consider you are merely talking to yourself.
I’ve been in touch with 3 big guys in this area of work. Nothing to report yet. Just trying to figure out what Steve did. Exactly.
bumped for UC. Read the comments to finally get a better understanding on exactly how the red noise was created.
Thks, TCO, I will read this ( in the days ahead ) . (Hey, I’ve commented something here earlier, can’t remember, this is a big big blog 😉 )
I can’t see any problem. As per bender’s comment 241, function acf estimates 28 autocorrelation coefficients from the proxy data, and those are passed to hosking.sim . I don’t know how hosking.sim makes the random series, but a matrix square root is one option to make series with a desired covariance matrix, as I mentioned in
http://www.climateaudit.org/?p=370#comment-124617
Other option would be to estimate only the one-lag correlation p, and pass a series p^n where n goes from 0 to 580 to hosking.sim. That would be AR1 process model, and probably the conclusions wouldn’t change at all.. Nothing to see here, now let’s get back to Mann’s uncertainties, much more interesting topic 😉
Not so quick, meestir.
RE Bender 15. Audit the gcm’s? There is only one way you can do that in a meaningfull way. Take a another somewhat related area. CFD (Computational Fluid Dynamics) and turbulence modeling. CFD is pretty good to get local and shortterm properies, but once you start integrate the flowfield to get oerall properties like total resistence your in trouble. An accuracy of +-100% is what you many times can expect. But! As long as you can do physical experiments, CFD is very usefull inspite of lack of accuracy in some respect.
With climate science you don’t have that. The only climate lab you have is the earth itself. The only way of proving or disproving the gcm’s predictions in 100 years is to wait 100 years. If they were right: halleluja! If they were wrong: hey, those gcm are 100 years old, we have much better now!
In my world a physical theory has no value unless you can verify it with experiment. As i see it, the only way to test the gcm is to find a way to build a small physical model of the earth in which you can speed up time. If the gcm could handle the small physical model they might handle the full scale to some degree. But if they would fail with the small model they would most surely fail with the full scale. But here’s the catch.
Why would any climate scientist try a way that has nothing to win and everything to loose?
Re: Andreas W (#54),
Well you could also study the climate of other planets…might actually be easier.
Re: Andreas W (#257),
Audit. Meaning dissect and expose. Sort of what Spencer Weart at RC claims is just not practical, even though it’s theoretically possible.
#54
But that’s exactly what they try to do. There’s a catch though. How can you possibly know that your small physical model of the earth is representative of the real earth?
Umm… I thought they tried to build COMPUTER models? Building a PHYSICAL model would be great fun, even at a relatively small scale, say, one to a thousand, you would still need a ball 8 miles in diameter. And then you would need to move it at relativistic speeds with respect to the observer to alter apparent time….
Perhaps we could enlarge the LHC?
Sorry to remain off-topic, but it just struck me that you would probably have to coat this putative model with custard to simulate the atmosphere at the appropriate Reynolds number, which makes the experiment even more attractive. We MUST get this on the budget list! Here is a link to one of my favourite talks, which talks about a broadly similar issue, Low Reynolds Number Swimming, from 1977: http://brodylab.eng.uci.edu/~jpbrody/reynolds/lowpurcell.html
You will note the apology in the notes above it – “Some essential hand waving could not be reproduced…”