Update: also see posts 382, 460, 462, 460.
We often hear a distinction made between “climate” and “weather”. It may surprise people that the famous mathematician, Benoit Mandelbrot, thought about this problem with completely opposite conclusions to realclimate. Mandelbrot is a prolific author who invented and popularized the concept of fractals . His popular book, The Fractal Geometry of Nature, is beautifully illustrated and well worth reading. Mandelbrot and Wallis [1969] not only considers the distinction between climate and weather, but considers earlier versions of many tree ring series in the infamous North American tree ring network. (This consideration seems to be completely lost to dendrochronologists.)
Here is an extended quote from Mandelbrot and Wallis [1969]:
Among the classical dicta of the philosophy of science is Descartes’ prescription to “divide every difficulty into portions that are easier to tackle than the whole…. This advice has been extraordinarily useful in classical physics because the boundaries between distinct sub-fields of physics are not arbitrary. They are intrinsic in the sense that phenomena in different fields interfere little with each other and that each field can be studied alone before the description of the mutual interactions is attempted.
Subdivision into fields is also practised outside classical physics. Consider for example, atmospheric science. Students of turbulence examine fluctuations with time scales of the order of seconds or minutes, meteorologists concentrate on days or weeks, specialists whom one might call macrometeorologists concentrate on periods of a few years, climatologists deal with centuries and finally paleoclimatologists are left to deal with all longer time scales. The science that supports hydrological engineering falls somewhere between macrometeorology and climatology.
The question then arises whether or not this division of labour is intrinsic to the subject matter. In our opinion, it is not in the sense that it does not seem possible when studying a field in the above list, to neglect its interactions with others, We therefore fear that the division of the study of fluctuations into distinct fields is mainly a matter of convenient labelling and is hardly more meaningful than either the classification of bits of rock into sand, pebbles, stones and boulders or the classification of enclosed water-covered areas into puddles, ponds, lakes and seas,
Take the examples of macrometeorology and climatology. They can be defined as the sciences of weather fluctuations on time scales respectively smaller and longer than one human lifetime. But more formal definitions need not be meaningful. That is, in order to be considered really distinct, macrometeorology and climatology should be shown by experiment to be ruled by clearly separated processes, In particular there should exist at least one time span on the order of one lifetime that is both long enough for micrometeorological fluctuations to be averaged out and short enough to avoid climate fluctuations…
It is therefore useful to discuss a more intuitive example of the difficulty that is encountered when two fields gradually merge into each other. We shall summarize the discussion in M1967s of the concept of the length of a seacoast or riverbank. Measure a coast with increasing precision starting with a very rough scale and dividing increasingly finer detail. For example walk a pair of dividers along a map and count the number of equal sides of length G of an open polygon whose vertices lie on the coast. When G is very large the length is obviously underestimated. When G is very small, the map is extremely precise, the approximate length L(G) accounts for a wealth of high-frequency details that are surely outside the realm of geography. As G is made very small, L(G) becomes meaninglessly large. Now consider the sequence of approximate length that correspond to a sequence of decreasing values of G. It may happen that L(G) increases steadily as G decreases, but it may happen that the zones in which L(G) increases are separated by one or more “shelves” in which L(G) is essentially constant. To define clearly the realm of geography, we think that it is necessary that a shelf exists for values of G near λ. where features of interest to the geographer satisfy G>=λ and geographically irrelevant features satisfy G much less than λ. If a shelf exists, we call G(λ) a “coast length”.
After this preliminary, let us return to the distinction between macrometeorology and climatology. It can be shown that to make these fields distinct, the spectral density of the fluctuations must have a clear-cut “dip” in the region of wavelengths near λ with large amounts of energy located on both sides. But in fact no clear-cut dip is ever observed.
When one wishes to determine whether or not such distinct regimes are in fact observed, short hydrological records of 50 or 100 years are of little use. Much longer records are needed; thus we followed Hurst in looking for very long records among the fossil weather data exemplified by varve thickness and tree ring indices. However even when the R/s diagrams are so extended, they still do not exhibit the kinds of breaks that identifies two distinct fields.
In summary the distinctions between macrometeorology and climatology or between climatology and Paleoclimatology are unquestionably useful in ordinary discourse. But they are not intrinsic to the underlying phenomena.
Mandelbrot calculates Hurst indices and 3rd and 4 th moments for 12 varve series, 27 tree ring series from western U.S. (no bristlecones), 9 precipitation series, 1 earthquake frequency series, 11 river series and 3 Paleozoic sediment series.
Reference:
Mandelbrot and Wallis, 1969. Global dependence in geophysical records, Water Resources Research 5, 321-340.




107 Comments
I thought the main reason climatologists separate climate and weather is to refute arguments on the lines of “how can you predict the climate in 50 years when you can’t predict the weather in two weeks”. To pursue Mandelbot’s analogy this is like saying “how can draw a map of the coast of the UK when you don’t know the details of how the coast fluctuates in any given ten yard stretch”.
Or have I missed the point?
yes….
re#2
🙂
Yes. What Mandelbrot is saying is that for a map the fine detail ceases to matter as you zoom out to view larger areas at coarser resolution. But for the weather there is no level of fine detail that ceases to matter as you zoom out to the coarser resolution of climate.
The weather, and hence the climate, is a chaotic system, it exhibits sensitive dependence on initial conditions, popularly known as the butterfly effect. Small differences in inputs produce results that can be wildly different. Among other things, this means that even if you had a perfect model of the atmosphere, if you put in say, 70 degrees for the temperature in New York and Boston, when in reality it was 71 and 69 respectively, you are going to get a prediction that deviates significantly from the real world after a while. It’s part of the reason weather forecasts fail beyond two weeks.
There’s an interesting discussion of this at http://climatesci.atmos.colostate.edu/?p=68. The funny part of the discussion is that the AGW guys, Schmidt and Connelly, admit it’s true but still want you to believe that climate can be predicted.
There is a sense in which it is true that climate could be predicted from averages of the weather. It would require a bazillion years of weather data at infinite resolution with no absolutely no changes in the earth’s climate system. With that in hand you could take very careful averages to make the predictions. Until then, I’d bet on changes in solar activity as the source of most warming, that tree rings are not temperature proxies, CO2 makes plants grow, and the AGW climate predictions are complete garbage.
My reading of the excerpt was that you should map the coast using an L which provides useful detail for the person using the map. Neither a map showing individual grains of sand nor one showing the entire planet would be useful for finding one’s way to the parking lot from the beach.
In weather/climatology neither the force of Hurricane Katrina nor the climate changes over the past 4 billion years give much information as to what has happened over the past 1,000 years.
Paul,
Thanks for the link to Pielke’s discussion of chaos theory. It very was interesting to read the two climate modellers defense of GCM. In fairness to both of them, when one’s career focus is an area that chaos theory indicates is barely worth a hill of beans, you can hardly blame them for being a little defensive.
That is indeed an interesting discussion. The best message of the thread is that by Mr. Clarke. However I generally agree with the warmers on this one. What’s being confused is that a particular action doesn’t have just one result. Consider a single molecule in the atmosphere. Just within a second it will interact with thousands of other molecules giving or taking momentum from each. Thus if such a single molecule has its momentum arbitrarily changed by some small amount it will soon affect which molecules are changed in what way. And even if our test molecule then escapes from the atmosphere, never to return, it will still have affected all these other molecules, so the information contained in it has not been lost as one writer claimed.
But it is true as others pointed out that we will never be able to observe these interactions and their myriad results. Therefore prediction is impossible, at least in a perfect sense. If we’re talking just measurable macroscopic properties, however, we can approximate as closely as we want things like pressure or temperature. But there are many things which require other things than just macroscopic measurements and they aren’t predictable (and they will eventually affect things like pressure and temperature). Among them are not just climate ‘tipping points’ but a gigantic number of things which are subsystems; things like Brownian motion can move submicroscopic actions up to the observable level.
Of course, none of this discussion is exactly real-world since we don’t live in a Newtonian world but a Quantum one and that truly will blur things and make prediction not just beyond human capability but total impossible.
Well, I’m not qualified to speak about the physics and maths of chaos theory, but I can and do observe my part of this planet.
When I go out I’ll observe not one butterfly, but millions of leaves all interacting with the wind, millions of flying inscets interacting with the wind as well no doubt too. Do their interactions mean that the weather now is completely different to that now or that tomorrow or next year? I don’t think so. It might be on a slightly differnet path, but it wont be as differnet as the word ‘choas’ implies, and it has to obey the laws of physics and the forcings invlved. We must ‘know’ what the weather an climate do, why else do we build rain fast houses in some places, tents in others? Becuase we know what that climate will do… if unperturbed.
This planet is like one model. It has one set of starting conditons. To me models are crude but they capture the jist of things becuase they clearly give predictons that are not way out of the bounds of reality. The planet could be at a temperature between absolute zero and infinity, but the models predict temps to rise just a few degrees. Pretty good I’d say! Moreover, if a lot of them point the same way they’re, imo, on to something – a lot do, they make sense with other physics too. Now, do models diverge because the starting conditons are all different? I think they do (but, I may have read this bit wrong elsewhere…) But earth isn’t a model…
So, why the concentration on chaos by sceptics? The use of it to ‘rubbish’ models? I think because people think it invalidates predictions they don’t like. I don’t think it does.
Dear Peter
chaos theory made an enormous impact, because what it suggests is so counter-intuitive. But it is still demonstrably true.
There are fixed mathematical equations. By changing a variable by 0.001, you can see a massive effect on your endpoint (5+ fold), whereas really large manipulation of the variable (doubling,etc), can have a trivial effect on the endpoint.
If weather is a chaotic system, then an infinitesimal perturbation could have a large and measurable effect on weather.
yours
per
Yes I agree with you up to here BUT…, and I’m asking the question, but in reality, by our experiences, it (weather/climate) doesn’t, does it? Neithr of these two things lurch about doing unpreditable (really unpredictable, things outside human experience) things. Right?
Peter,
One is given the illusion that the GCM’s do fairly well because they don’t fly off into wild predictions of future climate. As you put it, “The planet could be at a temperature between absolute zero and infinity, but the models predict temps to rise just a few degrees. Pretty good I’d say!”
If the models where built strictly from our knowledge of climate forcings, indeed, they would fly off into obviously incorrect predictions of future climate. To prevent this, arbitrary feedbacks are built into the models to stop this from happening. Modelers may claim that these feedbacks are not arbitrary because they must exist, otherwise real climate would fuctuate madly. This is the same type of circular argument one often finds in religion.
All the GCM’s are extremely simple when compared to actual climate, and they all have the same fundamental assumption that the fluctuation of CO2 is a major driver of climate change, even though we have very little real world data to support that claim. That is why the ‘Hockey Stick’ is absolutely essential to the AGW argument. If CO2 didn’t change much in the few thousand years before the industrial revolution, then climate must have been stable, the argument goes.
M & M have done a great job in pointing out the mathematical, statistical and procedural flaws in the Hockey Stick analysis. So it looks like we are back to a climate that goes through ‘natural’ cycles of warming and cooling. The GCM’s have no ability to predict these cycles because they do not even recognize that they exist or the mechanisms that cause them. For the GCM’s, the only significant climate driver is CO2. The fact that all the models generally come up with similar solutions is a function of the initial assumptions and arbitrary ‘governors’ on their equations to prevent run-away solutions, not a testament to their ability to accurately model real climate. Simply put, the models are designed to produce the expected answer, and so they do.
Re #11, you start quite well, then go off the rails.
What’s all this about ‘If CO2 didn’t change much in the few thousand years before the industrial revolution, then climate must have been stable, the argument goes’? No, if all forcings we stable, not just CO2. As I understand it the forcings changes look minimal, so the changes probably were.
What’s all this about ‘For the GCM’s, the only significant climate driver is CO2.’? Where on earth did you get that from? If you perturb models with varying CO2 conc you get differnt results. But CO2 palpably obviously isn’t the only climate driver.
What’s all this about ‘M & M have done a great job in pointing out the mathematical, statistical and procedural flaws in the Hockey Stick analysis. So it looks like we are back to a climate that goes through “natural’ cycles of warming and cooling.’? OK, lets leave aside whether they’re found meaningful flaws, M&M absolutely do not claim to say anything about past climate – read what they say here! If you’re relying on past ideas about climate, Lamb?, then we really knew a lot less then than we do now, so if you wont rely on what we know now I can’t see what we knew when we knew less is a better thing to rely on?
I’m afraid you’re believing what you want to believe about climate models.
Re #4. As I read the Mandelbrot excerpt his main point is that long term climate fluctuations are mathematically the same kind of thing as short term weather fluctuations and you can’t find a point where one discipline gives way to the other as you increase the timescale. There are no “shelves”. I don’t think it is true. Even if it is true I don’t think it necessarily invalidates climate modelling.
1) Is it true?
Isn’t there a shelf at about 10 years? Short term fluctuations in the weather such as North Atlantic high or an El Nino will affect climate figures for a year or two – but not averages over the 10-15 year scale. For example, can we not predict the average minimum temperature for New York in June for the next 10 years with some confidence and accuracy? And can’t we do this without having to concern ourselves with the fine detail of the weather?
Once we go longer than 10-15 years than different processes come into play – of which the composition of the atmosphere is one.
2) If it is true – so what?
If it is true then in Mandelbrot’s terms L(G) varies continuously with G. Going back to the geographical analogy: even if L(G) were to vary continuously it still would be possible for a geographer to draw a coarse map without knowing the fine detail of the coast.
I guess the key difference is that in the case of the coastline small perturbations cannot cause large changes – the large fluctuations are just the accumulation of the small ones. In the case of the weather/climate there is some reason to believe that small fluctuations can cause large ones. But as Peter points out – in practice there seem to be limits to this. Does anyone serious believe that a butterfly flapping can cause an ice-age? There are an awful lot of butterfly wings flapping every year – and not much to show for it.
Per,
with respect, but chaos cannot be theorised by definition.
Re #13:
I think the point is that Mandelbrot sees much the same sort of changeability within the climate whether he looks on yearly, 10-yearly, century or millennial timescales. I don’t think this either endorses or refutes models – he’s not talking about the mechanisms, just about the observed changes.
What it does rather refute is the notion of “stable climate”.
A few points about the Mandelbrot post:
First, the operational definition of climate as opposed to weather is arbitrary and heuristic. Linacre’s book (1992) surveys a range of them and distills it to a few vague sentences (I quote it in http://www.uoguelph.ca/~rmckitri/research/econ-persp.pdf). But there is a statistical implication, namely that it is a time scale of averaging at which new properties emerge in the average that are not observed in the raw observations. There are now long enough time scales of data to test for the emergence of properties like stationarity and antipersistence which are implied by the intuitive meaning of climate. I’ve had occasion to refer to Karner’s time series work before, and one of the other specific points he tests for is the existence of a “climate time scale” (Tsonis and Elsner also have written about this). The only scale break detectable in the data series is at a few weeks. There is no sign that a scale break emerges at 20 or 30 years. Mandelbrot’s last paragraph is confirmed in the most up-to-date and direct tests.
Second, not to toot the old horn too much, but Taken By Storm chapter 3 is all about the problem discussed above, namely whether talking about “climate” time and space scales actually allows the researcher to sweep aside all the fatal complexities known to exist on the local, daily time scale. The answer is no, for fundamental reasons. Averaging does not intrinsically remove chaos. An averaging process is involved going up from the atomic scale via kinetic theory to the level of fluid motions, but chaos emerges at that scale (ie the averaged quantities exhibit chaotic behaviour). In that case averaging introduces the chaos. There is no reason to assume that averaging up further to the climate scale removes it. Also, the theory exists to explain the changes in behaviour from the atomic scale to the fluid scale, but it doesn’t exist to explain the emergence of properties on the climate scale. However, where the theory ends the behaviour is turbulent and chaotic, and gives no clue as to details that can be ignored; it only says that there is no level of detail too small to matter.
Finally the example of distance does not carry over exactly to the climate problem, since distance is extensive (summable) whereas temperature is intensive (not summable), so concepts like measurement norms and averages cannot be readily invoked for temperature as they can for distance. In other words the “length of coastline” problem is still a simpler one than the “temperature of the climate”.
#8, Peter “So, why the concentration on chaos by sceptics? The use of it to “rubbish’ models? I think because people think it invalidates predictions they don’t like. I don’t think it does.” Yes it does. Look at the figures at the end of http://planetmath.org/encyclopedia/LorenzEquation.html. They are solutions to the Lorenz equations, first developed in 1963 as a toy model of the atmosphere. Look at the behavior at the right side of the plots, the curves go up and down in an unpredictable way, but within limits. No matter how long you run the solution on a computer it always does this and never settles down. What’s more, all the parameters of the equations are fixed, there are no changing “forcings.”
In any model of the atmosphere, you get this kind of behavior writ large. It will stay within bounds but oscillate around in an unpredictable way forever. There is no “steady state”.
BTW, there is no need to invoke quantum mechanics here, this is a purely Newtonian phenomenon that comes about from the nonlinearities in the system.
Mandelbrot distinguished his issues from Lorenz’ issues. Mandelbrot’s point is that you have variability on all scales.
Concepts like average can of course be invoked for temperature and other intensive quantitities. See here. In fact, temperature is nothing but an average.
Paul,
I disagree that quantum mechanics need not be considered, except in one sense. It’s true that the quantum mechanical model converges to the Newtonian model at sufficiently high quantum number and it’s possible that the agreement of a Newtonian Chaos theory with a Quantum Chaos theory will be high enough for a particular purpose but that has to be shown in a particular case, not just assumed. The point is that Chaos theory requires initial conditions to be known to arbitrary accuracy and quantum mechanics explicitly denies the possibility of such accuracy (usual caveats assumed).
So when does the accuracy of knowledge of initial conditions get to a sufficient number of digits that Plank’s Constant comes into play? I don’t know off-hand, but it’s not sufficient to say, “We’re dealing with macroscopic objects so QM doesn’t apply”. Such macroscopic objects have quantum hair on the outside and quantum worms inside (so to speak) which make their bulk meaningless when there are sufficient numbers of them.
Of course when the purpose of invoking Chaos is to show something can’t be predicted anyway, showing that quantum mechanics makes even chaos uncertain may be considered to be a case of gilding the lily, but it might have practical application in certain circumstances.
In principle you are correct, quantum mechanics ultimately determines the ability to specify initial conditions and adds its own indeterminacy via Heisenberg. In practice, the issue for accurately predicting climate in the long term is going to be some totally impracticable requirement for initial conditions like measuring the temperature in the lower 5 km of atmosphere on a 10 m grid to an accuracy of 0.001 C at every grid point. This is the type of issue that kills forecasts long before one reaches a quantum mechanical scale.
“Mandelbrot distinguished his issues from Lorenz’ issues. Mandelbrot’s point is that you have variability on all scales.” There’s no distinction. You have variability on all scales because the small scales feed into the larger scales via sensitive dependence on initial conditions.
Paul re #17 and #20. I think we might agree more than you think, but, if weather and climate are as chaotic as I think you’re saying how come, admittedly massive, computers with very limited data (certainly not as post #20 call for) can predict them at all? I think it’s because there is clearly some predictabilty to both.
It seems to me we debating degrees of, lay term alert, ‘chaoticness’. I do think weather and climate clearly chaotic (as per fact, Lorenz and the rest), but I also think the time and effort being put into the forecasting of both suggest a lot of fine minds think useful prediction of this chaotic system possible. Why? Here’s a phrase that caught my eye from William Connolley ‘OTOH the butterfly stuff is often misused: a butterfly flapping its wings will certainly lead to totally different global weather in a months time, and within a year is rather likely to cause a tornado to appear somewhere that it wouldn’t otherwise have done; but of course other tornadoes that would have appeared, won’t. The mistake-in-interpretation that I think people make is to think that the *energy* for the tornado comes from the butterfly, which is obviously wrong’. I don’t know if he’s right, but it sounds more right to me than some of the comments I’ve read. There a lot of butterflies out there effecting a lot initial conditions, but it the sun what drives the weather (and ghg’s that give it ~33C extra fizz) no amount of chaos will alter that physical fact. Right?
Let’s do the quick numbers…
circumfrence of earth = 40,000 Km (initially by definition)
radius = 40,000/2 pi
Surface area = 4 pi R^2 = 4 x 20,000 x 20,000 / pi =~ 5×10^8 sq Km. so the total number of your 10m grid points is 100 x 100 x 500 x 5 x 10^8 = 2.5 x 10^15. Next we have the accuracy of the temperature, which actually amounts to about 1 part in 10^5 since the temperature can change by +- several tens of degrees. Then we have pressure differences which help determine winds. How accurately would we need to know that and to what extent is the pressure implicit in the temperature? Then we have to have parameters for humidity and surface temperature and solar constant, but again we need to know how they interact with each other. I have no idea how do this but I expect that the total ‘factor’ we end up with will be something like 10^25 or more. Now Planck’s constant is 6.6 x 10^27 erg-seconds so you can see that if we consider what will happen to the earth’s atmosphere in the course of a few hundred seconds is likely to have had some interaction of a purely quantum nature somewhere and that change, over and above what could be calculated in a Newtonian manner will then need to be allowed for in your futile attempt to predict the weather / climate.
Of course the above is very schematic, but it at least gives us a bit of an idea about how things compare. QM on such a course grid as you propose would be marginally important on a climactic scale, but not probably on a short time scale.
I’m not particularly impressed by butterfly effect arguments either and that’s not what was on my mind (or Mandelbrot’s). Paul, I disagree with your assertion that Lorenz chaos and Mandelbrot effects are the “same”; Mandelbrot definitely thought not.
Or if you look at Klemeà…⟠take on long-term variability, you need look no further than long-term “storage” of energy in things like glaciers, or even in stratified ocean layers. If you add on geological changes, Milankowitch cycles never recur in quite the same way: it looks to me like there are measureable changes in Tibet over the Pleistocene for example so that the present interglacial is not going to be the same as earlier interglacials.
That’s what I’m thinking about , rather than butterfly wing effects.
Steve, the effects that you refer to are not due to the fluid dynamics of the atmosphere and the oceans, areas where chaos is applicable. Chaos is definitely part of what Mandelbrot is talking about when he says there is no distinction between macrometerology and climatology. There’s some goal-post moving in your argument since I thought the issue was prediction of the climate a few decades out. Once geological time scales are under discussion there are bound to be any number of effects beyond the fluid dynamics.
Ross McKitrick writes
This is not correct. Not only can you average temperatures, temperature is an average. (The average kinetic energy of the particles.)
Re #9:
Peter, we really don’t “know” what the climate is going to do. Normally on human time-scales the climate in one place does not change too much, so we get used to it and mistakenly think that it will never change, after all it has not changed in our life-time. But as we know it does change, and in big ways. Witness the ice ages.
Anyone that has done any modeling can tell you that the cardnal rule is “All models are wrong. Some are useful.” I’ve learned the hard way not to trust models too much. You never understand the thing you are modeling as well as you think you do.
Only at thermal equilibrium. Since the earth’s atmosphere is demonstrably not in thermal equilibrium at any scale (since it is chaotic and turbulent) your point is meaningless to what Ross said.
Re #25. This definition of temperature is for “kinetic Temperature” only – a more general definition is “the inverse of the rate of change of entropy with internal energy”.
See http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/temper2.html
Re #27 and #28 – I don’t buy Ross’s position on this. I think he needs to be more pragmatic. We use mean temperatures all the time, especially means for one location over time, and they work just fine. If someone tells me that the mean August high in Marseille is 2 degrees higher than London then that is a solid indication of a real difference in the climate. And if that difference were to change over 10 years that would be significant and represent a change in heat.
In the environment we are talking about temperature is not a bad proxy for kinetic energy. We aren’t talking about very sophisticated calculations – just whether the mean is a reasonable way of representing change.
Ross also seems to think that you can’t average intensive variables. Which is wrong. You can’t add them, but you can certainly average them.
Re #26 we do ‘know’ in the broad, not pedantic sense of some here, that I’m using it. I think Mark puts it well in post #29.
This is priceless.
http://pruffle.mit.edu/3.00/Lecture_03_web/node2.html
I beg to differ: all potential fields are intensive variables, like magnetic field, gravity field, electric potential or even pressure. You bet you can calculate averages for these, and they do have physical meaning.
Try reading Alonso and Finn, Fundamental University Physics, Book III Fields and Waves.
One of the points Ross and Chris made in Taken by Storm is that there is an infinite number of possible global averages (in fact, even in a small space, such as a single classroom, an infinite number of possibilities exists). That discussion alone is worth the price of the book.
When it comes to climate, we’re very data-poor. Only a few tens of tousands of surface stations exist to characterize climate, and this number has been dwindling. Many significant parts of the planet are very poorly characterized.
The modeler Michael Schlesinger said once that there are 14 scales of motion in the atmosphere, from the global scale at the top end to the molecular scale at the bottom. Models can resolve the first three (global, synoptic and mesoscale). To jump to step 4 will require orders of magnitude more computer power than we have at present, and that still leaves 10.
There are several versions of the old saying about big and little whorls. The one I remember is “Big whorls feed on little whorls and so on to vorticity.” Mandelbrot’s thesis is that the closer we look the more connections we see. If all we can see are the big whorls, we’re probably missing a great deal.
Re: #30
If you can’t add them how can you average them?
Mandelbrot is hard to summarize and I’ve obviously not conveyed the salient point here, because this has diverged into other people’s hobbyhorses. Let me say that I don’t get the point about averaging in Taken by Storm either. Chris Essex is an accomplished thermodynamicist and I’m sure that his point is not one that is refuted by a high school argument. Having said that, I don’t understand why it isn’t refuted by a high school argument.
Rather than huffing and puffing about global averages and is at a dead end in this discussion, can I suggest that people try a different problem which is more Mandelbrotian in spirit – calculating the time-variance of global temperature? I’m really more interested in time series issues – there are lots of stochastic processes for which there is no second moment, Mandelbrot identifies lots of them. If you have variability on all scales, how do you know that there is a second moment – i.e. calculable variance?
Can we try this time series question before we have any more discussion of # of stations or intensive fields?
Its odd that the invocation of chaos theory is assumed to be attractive only to climate sceptics. In fact Al Gore in Earth in the Balance invokes Chaos Theory in support of his quasi-religious vision. This is the looniest invocation since Jeff Goldbum’s character in Jurassic Park explained how Chaos Theory clearly predicted that the dinosaurs would get loose.
Chaos Theory is something like Marcel Proust. At a cocktail party you can always discuss Proust even if you’ve never read him. You are guaranteed to make a favorable impression.
For example, discourse on how Proust presages the Green Movement in Germany. Or if you had rather, discourse on how Chaos Theory does. Try not to wave your arms about too much. It hurts credibility.
Chaos Theory is unified mathmatically but it’s impact comes from a series of discrete messages or lessons.
Lesson #1 – Self similarity
This is the point of Mandelbrot’s article. The Mandelbrot set defines a border that looks the same at all scales. The coast line of Norway appears to exhibit this behavior (within limits). Is the border of climate self similar with weather? The language is discrete (climate, weather) and so connotes a difference in kind. Is this a valid distinction?
There is clearly one aspect of climate modeling that differs substantially from weather modeling. Weather models are subject to empirical and statistical analysis because the best models for tommorow’s weather may be determined the day after tommorow. Climate models may only be judged analytically because of the human time scale. The next lesson shows some of the limitations that Chaos Theory imposes on analytical judgements.
Lesson #2 – Initial Conditions
There is, I believe, real randomness in the physical world. True random events bubble up from the quantum level. Their occurance cannot be predicted even with perfect knowledge. They can of course be treated statistically. Quantum mechanics was a shock to modern man because it had been assumed that ever better knowledge would soon allow us to know the world deterministically not just statistically.
Chaos Theory was the second shock. It was shown that simple equations often led to complex graphs. That was originally thought to be OK because every value on the graph was deterministically derived. However the intiating value had to be exact. Small differences at the starting pont might yield big differences later. Again in the real world pure determinism cannot be obtained – ever.
This is the lesson that climate modelers fear. Lomborg points out that all the IPCC models round up the initial warming measurement from .6 C to 1.0 C. This is a substantial change in initial conditions. It is much more than a butterfly in Peking.
Lesson #3 – Strange Attractors
This is the lesson that Al Gore invoked, however he misses the point completely.
It has long been known that there are bi-stable phenomena in the physical world. Among the best known is the ENSO. It isn’t clear intuitively why this should be. The mathematical phenomenon of strange attractors provides a possible explanation or a heuristic.
Many simple mathematical series proceed to an end point in a straight forward fashion that is easy to graph and to understand. However some seemingly simple equations exhibit odd (chaotic) behavior. Again the behavior is mathematically deterministic albeit physically unpredictable.
The path of a strange attractor approaches one focus and then seemingly at random switches to another focus. Notice that this mathematicaly behavior is bi-stable without an outside ‘forcing’. Al Gore cautioned us that the Earth’s climate is bi-stable. He invoked Chaos Theory then to argue that we should not disturb the ‘delicate balance’.
In fact if you believe that strange attractors are a good model for ENSO and similar climate phenomena you should not worry about anything. The oscillation of El Nino then is independently and intrinsically caused. It oscillates because of its unpredictable intrinsic mathematical behavior.
If climate, as Al Gore claims, exhibits the characteristics of Chaos Theory (Strange Attractors), then no one is to blame for any climate change. Strange attractors mean never having to say you’re sorry.
Conclusions
Chaos Theory like the Heisenberg Uncertainty principle, and Godel’s Incompletness Theorem is a limitation on what we can know. As such it doesn’t so much tell us what is or what will be as it warns us about epistomological hubris.
I won’t wear out my welcome with Steve by provoking an average temperature donnybrook on this thread. It took me a long time to get the intuition, so I am entirely sympathetic to those who don’t buy it, and I presented most of the above objections myself (and other ones besides) en route to conceding the point. For the genuinely curious the math is not overly hard and will, hopefully, be in print in a proper science journal before too long. Bottom line here: the distinction between equilibrium and nonequilibrium is essential. Of course you can “average” temperatures sampled from subsystems out of equilibrium with each other, in the sense that your computer will oblige and the police won’t show up at your door. And there are circumstances in which the resulting number has useful intuitive meaning, eg whether to pack a sweater or a bathing suit. But the resulting number does not have the same physical meaning as the raw data on which the calculations were done, and in the analysis of the global climate system over time the theoretical problems created by this distinction are important and cannot be waived away.
One thing which hasn’t been brought up but which is important when Chaos is discussed is that it’s possible to ‘entrain’ a chaotic situation. This is why climate isn’t purely random. Mountains, deserts, seasons, etc. force certain patterns on the underlyingly chaotic atmosphere.
I remember reading a paper concerning how the the heart’s native pacemaker is intrinsically chaotic but that over time as it’s developing, or later via electric shocks the feedbacks in the system keep the system steady and under control. The same is undoubtedly true in the case of the climate, but knowing what feedbacks exist is vital. What I see being done by the warmers is to pick a few known feedbacks and assume they’re all the important ones that exist and that we understand how they interact well enough to make prescriptions for policy. Most skeptics, I’m sure, disagree with both assumptions.
Yeah…I knew that was your main point and I’m waiting to hear people engage on it. Somehow, both the post itself and your recent remark are hard to engage on, Steve. You need to spoonfeed us.
I do agree that the temp averaging and butterfly stuff is sorta off-topic, but they do represent efforts to engage intuitively with the ideas/topic.
Let me break down and try to read and parse your selection…
I like the phrase: “the classification of bits of rock into sand, pebbles, stones and boulders or the classification of enclosed water-covered areas into puddles, ponds, lakes and seas” as a counter to pontificating about weather and climate. If you have Mandelbrot-type autocorrelation, why are [time] averages or 2nd moments of “climatology” not themselves as transitory as the global average temperature or variance from 3 to 4 pm EST on April 11, 1956? I’m not saying that they are. I just want to know why not?
The obvious difference between weather and climate has to do with seasonality, Steve. At Canoe U (surely not a leading meteorology school), I heard a prof say that weather is about what’s going to happen tonight. climate is about what in general will happen tonight. saying that it will be humid in July with a chance of thunderstorms in Southern Maryland is not “weather”, it’s climate. Because I can say that right now in October. So I think there is some point to the comment that climate is very different from weather in that sense.
The Mandelbrot post seems to make the point that fluctions on a decadal scale versus centenial scale may have no clear divider. this is a much different point than saying that daily weather and “climate” (in general) are best studied in the same manner.
Time scale seems is connected to averages. When you take data, whether you record it manually, or upload it into a computer you are not obtaining an instantaneous data point. Sensors are noisy. Therefore, whether you have an analog or digital readout, what you see is damped, or averaged over time. When you record a series of data points, each one is actually an average. This time period in between the data points may differ significantly from the data point at the start and end of this time period. The average may or may not include readings from the entire period. Perhaps you do not want to include every spike in the data, since some spikes are caused by electrical surges, induced currents, or some other anamoly.
These data points are then averaged over some period of time to give hourly, daily, weekly, monthly, or longer time period averages. Looking at weather/climate data for a certain geographic reagion means that several data sets are averaged together. Do these data sets represent the entire region so that we can rightly call them a regional average? Probably not.
For a global average, you take many data sets and average them together over a certain time interval. What about the places which have no data collection stations? Is the global average truly global? With some stations openning and others closing over decades, is the average from one time period even comparable with the averages from the periods before or after it?
Long time period averages are actually composed of averages of averages of averages of averages down to the average number of electrons coming from the sensors. I won’t get into quantum effects. Each of these averages may miss certain periods of time as well as many locations. We say that a global average monthly temperature truly represents the average temperature of the entire planet over last September (or any time period), but it really represents parts of the planet during some of the time during September. Let’s now compare this September’s average to a September 50 or 100 years ago. Are the same locations in both averages? Are the some time frames included? What about the response time of the instruments. Are they comparable?
My post above should read: “Time scale is connected to averages”
Brooks,
While your points need to be considered while designing experiments, when we’re examining data once collected the major question to be asked is whether the data is biased or not. If the actual temperature as represented by mesurement A is just as likely to be too high as too low then the data is unbiased and we can average it with other measurements and, given enough such measurements we can even come up with averages of greater accuracy than the individual measurements (though that’s tricky and requires further examination of what sort of unbiasness we’re dealing with.)
Re #39 and #46
Dave, err, somethings wrong because I agree with these posts (yes, honestly) bar this sentence in #39 “What I see being done by the warmers is to pick a few known feedbacks and assume they’re all the important ones that exist and that we understand how they interact well enough to make prescriptions for policy”. Do you think there are significant unknown feedbacks? If so how have they escaped detection? And why do you still think ‘warmers’ so dishonest and so unknowing?
re 43
Annual average station temperature is highly correlated over 1000 km and then breaks down. So the longer the period the longer the correlation distance.
However, the global average is not a good predictor for individual regions,
but strangely individual stations _are_ good predictors for regional averages.
We therefore cannot predict if temperature will rise at all in central antarctica, based on the global average.
see also my classic european compilation:
http://home.casema.nl/errenwijlens/co2/europe.htm
wtf does this post have to do with 43? Sheesh.
Re: 46, Peter, you ask “do you think are there significant unknown feedbacks”.
Recently, it was discovered that phytoplankton can affect the weather above them, by emitting substances that serve as cloud nuclei. The increase in clouds, of course, cools the area underneath the clouds, and the plankton cool down. Given the numbers and large distribution of plankton, this is obviously a significant feedback, one which was previously unknown. A similar effect has been discovered over forests.
So, yes, given that one was discovered just this year, I do think there are still signficant unknown feedbacks.
To your other question, how have they escaped detection? Well … umm … err … they escaped detection the old-fashioned way — nobody noticed them, just as no one noticed the feedback from the plankton. Did you notice the plankton feedback? I know I didn’t. That’s why they’re called “unknown” feedbacks.
I doubt very much that this discovery of plankton and forest feedback marks the final uncovering of the last unknown significant feedback. Since you obviously don’t think so, I have to ask the basis of your certainty …
w.
PS – I know you asked your last question, “And why do you still think “warmers’ so dishonest and so unknowing?” of Dave, but I’ll give you my answer to compare with his.
First, I don’t think anyone of note thinks all warmers are “dishonest” and “unknowing”. Some, however, clearly are one, the other, or both. As a result, climate “science” is in a shambles. If you want dishonesty, take a look at Mann et. al. and their responses to simple scientific questions. If you want “unknowing”, check out the claims of the modellers versus the (un)reality of their model when they are checked out against real historical data. Anyone who claims that a slight resemblance in the trend over some period shows that a model is correct is deliberately ignoring all of the rest of the ways that we measure results (standard deviation, IQR, Hurst exponent, autocorrelation, etc. ad. infinitum). To me, that spells “unknowing”
read! sheesh.
Peter, I had a message ready to post but it was too political in tone. Suffice it to say I think a number of warmers think the end justifies the means and that this even applies to science.
Hans, Re: 47
Thanks for the comments and the link to your graphs.
Did you adjust the data for UHI?
As you asked for an example.
I have seen in many places (less so here) where even the thought of solar output effecting climate is derided. To the point that those doing the derision were amazed at the stupidity of anyone who could even think that solar output had anything to do with climate.
While I wouldn’t think that many people here would be so obtuse as to exclude solar output in any climate equation, I would make note of the point that variances of solar output are rarely discussed in “warmer” circles in relation to “Climate Change”.
I would think that the very first thing one would look to, as a researcher, as to what might be showing a century long trend towards warming would be solar output, if for no other reason to subtract it from the gross trend to isolate any anthropogenic signals. Yet in any of the literature I rarely see a mention, much less a graph, showing solar output in the past, lets say 150 years, or to correlate to something like the Hockey stick let’s say 1000 years, wouldn’t it be nice if we had some data showing the trends since let’s say the beginning of industrialization, I mean it has to have some relevance to the discussion.
Well after much searching over years I did find something. Jeff bless the wonders of the Wiki.
“Carbon-14 record for last 1,100 years (inverted scale). Solar activity events labeled”
You will note that this graph is reverse of norm, with present day being on the far left, going into the past towards the right.
You will of course note an upward trend starting at approximately 1900
You will not a similar trend here starting, again, at approx 1900.
Definitely not an “Unknown feedback”, yet certainly not a well publicized one. Think of it as the Harry Dean Stanton of climate data. Not very well known, but highly pervasive.
Sorry I almost forgot. Quoting the IPCC
“Climate response to solar variability may involve amplification of climate modes which the GCMs do not typically include.”
Emphasis is mine.
Hans,
re: “Annual average station temperature is highly correlated over 1000 km and then breaks down.”
In terms of year to year changes of differences of annual mean temperatures, how small would you say would constitute highly correlated?
#53. One of the regular commenters here has written a monograph that you might be interested in reading. “The Role of the Sun in Climate Change” by Douglas Hoyt & Kenneth Schatten.
There is also a very interesting idea that couples solar activity to climate via the solar wind and shielding of cosmic rays. It seems to work quite well and doesn’t need any GCM’s to explain past climate. By its nature it makes it difficult to predict future climate, unless you can predict solar cycles. http://www.dsri.dk/~hsv/Noter/solsys99.html
Re #46:
Peter, I for one do think that “warmers” are unknowning, in the sense that there are surely some things about global climate that they don’t know. At one point nobody knew that E=MC^2 or that the earth is round. That does not mean everybody was stupid, just that certain discoveries had not been made yet.
I find it very annoying that you ascribe a personal attack to all questioning of the AGW theories and thier authors. Just because someone is asking questions it does not mean they think the authors are dishonest or stupid. It’s a tactic that’s used to put people on the defensive, but it won’t work here.
re 52
yes
http://home.casema.nl/errenwijlens/co2/homogen.htm
re #46
As far as I remember it’s quite widely acknowledged – you may even find it somewhere in RealClimate – that neither the amplitude nor the direction of feedback due to clouds is capable of being modelled.
re #53
Somewhere on this site you should find a link to von Storch’s “Erik the Red” exercise, where a climate model was run backwards for the last 1K years or so using solar forcing records. (It’s the data he used to prove that MBH’s method wildly underestimates past climate variability, even when fed with good temperature proxies.)
The result is not at all like a hockey stick, well at least not one you’d want to use…
Here is another proof that MBH’s method wildly underestimates past climate variability

Average of Hohenpeissenberg and Vienna compared with Mann et al.
Source for Mann et al data: http://picasso.ngdc.noaa.gov/cgi-bin/paleo/mannmapxy.pl?lat=47.5000&lon=12.5000&gridcell=37&filename=grid37.dat
Re #59 ahh, and seriously, that’s a known unknown not an unknown unknown.
Re others, I accept we discover new feedbacks, but I doubt (that’s all) feedbacks that are significant (by which I mean big, AGW reversing or AGW doubling) are still to be found. I also don’t see why, if there are some big feedbacks to be discovered, any reason why they need be -ve rather than +ve (unless one spends time just looking for the one and not the other) – they’re by definition undiscovered and unknown unless one believes the ones left to be discovered must be -ve cooling ones that is….
Re #57 and my percieved personnal attacks. Here’s a nice one from #49 “If you want dishonesty, take a look at Mann et. al. and their responses to simple scientific questions.” Perhaps they only count if they’re from me, or are only a personnal attack if you think what’s said is untrue and that, therefore, anyone who disagrees must be wrong?
re # 62
Sorry, didn’t realise you meant unknown unknowns. Don’t know how anybody could know about those (except of course that there’s this giant pan-dimensional Quantum Boodlum in the lower stratosphere…)
AS Donald Rumsfeld put it.
“We also know there are known unknowns; that is to say we know there are some things we do not know. But there are also unknown unknowns — the ones we don’t know we don’t know”
It must make people proud to be Americans.
Peter,
Re: 62
GW”€°⟁GW
You could say that f(GW)=AGW, however I have yet to see the mathematics of this function. At any particular point, the ratio of AGW/GW would lie between 0 and 1, but this is not very helpful.
Since any unknown forcings effect GW, it then follows that they also effect f(GW). It is not the other way around.
Peter,
I should also add that there are some people who believe that the ratio AGW/GW is greater than 1.0. I do not share this belief.
Why not Brooks? If you accept that we don’t really understand what’s going on, isn’t a next step that we may very well have a natural cooling trend limiting GW from being high?
Following up on #67, couldn’t it be argued that it’s only the AGW which is keeping us from sliding into a possibly overdue ice age; or at least another little-ice age. Would any of the precautionary principalists on the warmer side want to argue that it’s better to have an earth 3-4 degrees C colder than now than one 3-4 degrees C warmer?
TCO and Dave,
I have often wondered how the GCMs handle changes in albedo from increased cloud cover. The key point of “nuclear winter” was that increased albedo would reduce the sun’s energey flux to the lower atmosphere and the earth’s surface causing significant cooling.
Re:#69
From what I’ve seen the GCMs divide the atmosphere into a number of layers and then each grid cell is given a certain % cloudiness for each layer based on the value of certain parameters within the cell. It’s a bit more complicated than that, but when we’re talking 5 deg square cells or whatever, it’s not a very fine-grained system. And it’s strictly parameter based rather than derived from any first-principles. The hope, of course, is that enough parameters are being used to do a decent job and that the large number of cells will let the errors wash out.
I’m sure it has some degree of accuracy, but remember we’re talking fractions of a degree C over decades and the absolute temperature is going to be in the 300 +- 50 range. So we’re talking about having to have the model give us a value greater than 99% accurate and maybe 99.9% accurate in terms of absolute temperature. Given the unknowns in just what the positive and negative feedbacks are on cloud formation and dissipation and how they’re affected by things much smaller than a cell, like jet exhausts, cooling towers, small mountain ranges, etc., it’s hard to see how they can be that accurate. And this doesn’t even include things being discussed in this thread like vortexes and butterflies.
Re: #62
Peter,
That’s a logical fallacy called “Two wrongs make a right”. According to your reasoning if I call you out for making personal attacks, and I don’t also call out everybody else for doing the same thing (according to you), then my criticism of you is invalid. Wrong.
Re#36 Steve, in the financial world, a time series is created by taking the natural log of the daily closing price of the S&P 500 and than taking the difference to create a returns series, ie r(n) ~ ln(1+r(n)) = ln(P(n+1)) – ln(P(n)). The histogram of the time series exhibits a long tailed behavior. A Mandelbrot view would be to model this histogram with perhaps a Cauchy probability density function (pdf) which doesn’t have a defined mean or variance. But practically, the returns series has finite bounds, so one could use a truncated Cauchy pdf that would provide a finite mean and variance. The other school of thought is to use a gaussian pdf with a time varying variance (actually correlated) to model the long tailed histogram. This approach leads to the Garch type modeling which is very popular now in the literature.
Re #57 Here’s a recent paper examining the contribution of solar flux variations to global temperature changes.
http://www.agu.org/pubs/crossref/2005/2005GL023849.shtml
ping
Patrick M. said:
You are right, they stickhandle that one like a hockey puck around a defenceman, twisting and turning, definitions shifting, sliding. As a goaltender, you must keep your eye on the puck. Or as Steve has suggested before watch the “pea under the thimble”. But to answer your question: one might issue a challenge to go through RC archives and COUNT the number of times they waffle on this one to suit their argument at the time.
Steve: I’m OK with this topic on the main board, but I’d prefer that it be attached to a relevant thread. There are so many threads that it’s hard to find, but let’s do this. I’m happy to suggest a thread and ping it, as I’ve done just now, pinging an old discussion of Mandelbrot opining on weather vs climate, an old discussion but Mandelbrot is a big name.
#60
Rind (2008) p. 858:
I agree with the main thrust of this, that there really isn’t some clear dividing line. Think about a certain phase of some major weather pattern; you’d expect the climate to be a certain way during a positive PDwhatever than a negative one. So is climate only averages? No, it’s areas and patterns. Certainly, what the climate is in summer is different than that of winter, desert different than jungle.
I tend to think of the global mean temperature anomaly trend not as climate, but rather as tracking heat levels over time by proxy. 🙂
But to the analogy, you don’t have to know what sand looks like or what kind it is or how it’s shaped, or the exact lines of a coast to know the general path. Nor is there any surprise that one coastline pretty much looks like another.
Climate’s what you expect, weather’s what you get.
Patterns can be averaged.
That knife isn’t as sharp as the alarmists require. We expected La Nina. We got El Nino. So what is ENSO*: climate or weather? (*Insert your favorite ocean fluid dynamic here.)
In case it isn’t obvious, I’m with Mandelbrot. Nice OP.
Suppose “climate” is defined as the time and space scale (L) at which local “weather” anomalies (noisy departures from the expected climatic mean) sum up to cancel each other out, thus yielding unambiguous deterministic responses to various external forcings.
Supposing that this actually happens in the real world – then what is “L”? 30 years + 1000km?
Recalling that we’ve only been seriously monitoring the oceans for less than a century, what are the realistic prospects for solving for “L”?
Next, how do we treat circulatory anomalies whose characteristic spatial and temporal scales span “L” (due to LTP)? In this case, they will be part noise, part signal. How do we partition? How do we handle GCMs that are incapable of generating realistic L-spanning phenomena? ICTZ, THC, ENSO, PDO, AO. How do we tune the GCMs or EBMs if we can not distinguish external “signal” from internal “noise” in the instrumental data?
Are these problems as trivial as the RC zealots make them out to be?
I guess that Gavin thinks that the distinction between climate and weather is more fundamental thank the classification of bits of rock, but it does seem like valid question.
“Climate is what you expect. Weather is what you get.”
What if what you “expect” is not statistically supported? i.e. You have no right to “expect” what you say you expect. What if time-averages over any short interval (t) are a poor indicator of a process x’s actual expectation, E(x)? What if x is subject not to white noise, not red noise, but 1/f noise?
Can 1/f noise processes be split cleanly into meteorological vs. climatic time scales?
The RC zealots assert “yes”. But how do they know?
1. Ray Pierrehumbert says the deep ocean turns over on an Order(1000) year time-scale. I believe him.
2. Gavin Schmidt says we don’t know the ocean’s full thermal state at any given time. I believe him.
If (1) and (2) are true, then how do we know ocean circulation is not a source of, say, 1/f noise? Doesn’t that have important implications for how we develop and treat the output from stochastic simulation models like GCMs?
I know I am stupid. But the voices in my head ask these questions. I can’t stop the questions.
Mitigate. Mitigate. Just, please, answer the questions. Make them go away.
74 (Mayson): The abstract of the Scafetta & West paper cited says:
Since most other analysis of TSI suggests that the ACRIM increase was spurious so would also the minimally [sic] contributed ~10-30% of global surface temperature warming seem to be.
Haloperidol for the voices, bender.
An interesting conundrum your voices have brought to light, btw. We can understand, presumably, the rate at which the ocean state changes, but we don’t know where along that time-line we are at, or better, what the state actually looks like right now, only that in O(1000) years, it should look similar to now.
I think you are correct that there are important implications. What if it is not noise-like, either, but subtly driven by an external force that we are not looking at closely enough to notice?
Mark
bender,
I don’t think most people have a clear idea of the consequences of 1/f noise. If I’m doing emission spectroscopy, I integrate (sum) the signal for a period of time to reduce high frequency noise. If the noise is white, then the longer I integrate, the more precise my result. With 1/f noise, the longer I integrate, the less precise my results. Signals aren’t pure 1/f, of course. So what happens is that there is an optimum integration time for maximum precision. For surface temperature, that optimum time could be on the order of 30 years. But fluctuations on time scales longer than 30 years can still be noise and not signal. If indicators like global temperature are subject to 1/f noise, then there is no bright line between climate and weather and separation of signal and noise is not trivial.
bender (#83; and DeWitt #86):
Wikipedia, echoing the unanimous position of serious researchers, supports this premise:
With respect to the second question,
is there any ambiguity? If the distinction between climate and meteorology is interpreted as the difference between signal and noise (i.e. ; deterministic versus stochastic), the answer from an operational perspective is no. Even with very long time series, it is hard to separate “signal” from “noise.” Mandelbrot addressed this in many places, including [Mandelbrot and Wallis, 1969, WRR 5(1)]:
In conclusion, I think I appreciate what you are going through. I, too, “can’t stop the questions.”
Leif
The majority is against your own particular stance on solar vs climate too so it’s odd for you to denigrate the minority position in anything. The use of the weasel word “suggests” doesn’t convince either.
In this respect, it is also salutory to review Klemeš thinking about fractional noise and persistence, linked in one of the pages in the top line of the thread (update). Klemeš’ highly plausible view was that persistence features in climate series pertained entirely to hydological processes as there were all sorts of processes that acted as “integrals” (I tend picture these things as inventory build-ups and drawdowns). Aside from things like lakes and oceans, things like glaciers, clouds and precipitation and, I suppose, even raindrops are nit just t-events but draw down or build up inventories of one thing or another. Klemeš derived LTP properties as a consequence of accumulations of such processes.
An image of El Ninos that intrigues me and I haven’t seen it discussed in precisely these terms, though the idea seems pretty obvious and directly connects El Nino to 1/f noise is this: [and, Atmoz, Eli, the following is just chit-chat and whether this makes any sense has NOTHING to do with the validity of my criticisms of Mann and the 1000 year proxies – so please don’t read any further) one of the simple models of 1/f noise are sandpile avalanches under steady drips of sand onto a pile. One of the characteristics of El Ninos is that they seem to be preceded by an increase in ocean elevation, which dissipates in an El Nino. So one can easily picture why ENSO time series could well have 1/f patterns. Indeed one would expect this. I saw an early article arguing that the original Nile series did not show “long-term memory” because it was connected to ENSO, but this really just moves the issue one stage back.
Well said, De Witt:
Interesting, TAC, that Wikipedia knows what RC doesn’t accept. [How long before Connolley alters that page?]
To bring it to a fine point. (A) What is causing the current flatline in global mean temperature? (B) Maybe it’s the same thing that caused 50% of the rise in GMT in the 1990s? i.e. Maybe the cause is not external, but internal? That would mean that it is “very, very wrong” to attibute as much GMT variaiton as possible to external deterministic forcing agents. If internal ocean hydrological noise is 1/f noise, then that may be enough to explain the unexplainable.
Note I am not denying a role for GHGs or the value of “mitigation”. I am simply hypothesizing that maybe the alarmism is not justified. Maybe the GHG effects are weaker than what “the consensus” thinks.
The plausibility of 1/f noise is justified by the dynamics of the THC. “Conveyer belt” processes – like rivers – are 1/f processes. That’s why Koutsoyiannis – a hydrologist – is on to something. There are rivers running in the ocean.
J. Peden, from another thread says:
It is a very real statistical problem. To treat it as a mere “word game” is to underestimate its foundational importance. One gets the defintions straight – using the unambiguous language of mathematics – so that there can be no doubt as to what is being claimed. Definitions having been formally laid out, the scientist can then proceed to solve the problem. Which, in GCM-based attribution terms, is about how much internal noise vs. external signal one can expect in any given “trend”.
[I am quoting Peden out of context, and do not disagree with his original point. Just want to illustrate that there *are* those who think it is nothing more than a semantic issue, fodder for those who love endless debate.]
Note that at one point, many people here claimed that climate was defined as the average over time only, without any spatial average, so this is progress.
>> Suppose “climate” is defined as the time and space scale (L) at which local “weather” anomalies (noisy departures from the expected climatic mean) sum up to cancel each other out, thus yielding unambiguous deterministic responses to various external forcings.
The only problem with this definition is the definition of weather, which refers to climate, causing a circular definition. Perhaps Weather should be defined as variations in atmospheric parameters (temp, humidity, etc) which are caused by atmospheric circulation.
>> Supposing that this actually happens in the real world – then what is “L”? 30 years + 1000km?
To satisfy the definition, we can use L = 1 month + entire globe
>> There are rivers running in the ocean.
I’ve said the same thing on this blog for a long time.
Geoff, on aother thread, quotes this interesting exchange:
And what if a substantial portion of that matching “trend” from the 20th c. is due to 1/f ocean noise? That would cause the variation attributable to external signal to drop proportionately. The magnitude of external forcings estimated using these same model may drop by that much or more.
Just hypothesizing. Just asking. Has this been considered? Please point to the paper (or section in the IPCC 4AR) where this has been mentioned, and dismissed as implausible.
We can. But *should* we? As the guy who doesn’t like arbitrary, subjective thresholds, this seems awfully arbitrary and subjective. But I gather that Gunnar agrees with Mandelbrot – that although it may be possible to separate out the characteristic time-scales of weather vs. climate, there are phenomena that span the threshold – “rivers in oceans” being one example.
Mathematics mavens tend to think in terms of ‘1/f noise’. Physics folk tend to think in terms of ‘energy equipartitioning’: that is, systems with 1/f noise have no preferred scale at which to dissipate their energies. As regards weather/climate, it has always been interesting to me that the unforced Navier-Stokes equations are (in their own way) scale-invariant. It is suggestive to
use that scale invariance and calculate as follows:
Form the Fourier power spectrum
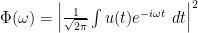
Scale by setting
by setting  and define
and define 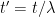
This is ‘1/f noise’. [Let me be the first to say that this is no proof of anything; but I think it is interesting nonetheless.]
>> As the guy who doesn’t like arbitrary, subjective thresholds, this seems awfully arbitrary and subjective.
LOL, touche. But to be fair, this is a conceptual definition, not a hypothesis, so this is something that we need a consensus on, otherwise, communication is hampered.
>> But I gather that Gunnar agrees with Mandelbrot – that although it may be possible to separate out the characteristic time-scales of weather vs. climate, there are phenomena that span the threshold
Yes, I do, because according to your definition, which I like, climate is about external forcings. As such, there are external forcing events which have short term effects, while there are internal weather variations which have long term effects.
Ahh, but short term weather events are also caused by short term external forcing changes (earth rotation & orbit). So maybe the definition should be:
Climate is the effect of the longer term average of external forcings.
Rather than theorize any further, let me put this issue in a due diligence context.
1. Is Mandelbrot’s view consistent with the IPCC consensus view?
2. Where, in IPCC 4AR, is “climate” and “internal climate variability” defined or discussed?
3. What is the consensus view on the nature of Earth’s “internal climate variability”?
4. What is the consensus view on the nature of modeled “internal climate variability”?
5. How does the IPCC consensus justify allocating as much variability as possible to external forcings, and assuming the remainder is “noise” – given that this will obviously tend to underestimate the noise and overestimate the signal?
6. Are the concepts of climatic “signal” and weather “noise” clearly defined in IPCC AR4?
7. Is the IPCC consensus view on “internal climate variability” sufficiently inclusive that it can really be called a “consensus”? Or have they selected a subpopulation of researchers who think along the same lines, leading to a false consensus more akin to groupthink?
8. If the consensus difference between “climate” and “weather” is “expectation” vs. “realization”, how does the consensus view intermediate-scale phenomena that are tantalizingly patterned a posteriori, yet nevertheless unpredictable a priori, such that expectations are rarely if ever realized? [Must not these phenomena be classified as “weather”? And can these phenomena not account for 10-30 year warming and cooling trends?]
9. How seriously is the alternative hypothesis considered that 20th c. warming could be a result of poorly understood “internal climate variability”? Does IPCC AR4 discuss this possibility? Do they dismiss it, or avoid discussion altogether?
These are auditing points that anyone could follow up on.
bender #97
Let me guess. AR(1). No LTP.
Mann & Lees 1996
..and so our story begins. Median-smoothed spectrums and partially centered PCs..
I came across this today -which suggests that the rain events themselves are similar to earthquakes or avalanches:
rain is earthquakes in the sky
#98 Great quote, UC. So AR(1) is a Team paradigm. No wonder RC dodges questions about Hurst and 1/f.
#98 Makes sense now why Gavin would suggest lucia base her noise model on GCM output. No way you’re going to get 1/f noise from GCMs – especially when they cherry-pick outputs that conform to their arbitrary criteria. Good for lucia choosing not to accept what the self-interested authorities recommend.
#99 If rain event size follows a scale-free distribution the way that earthquakes do, then maybe hurricanes do as well? David Smith? Ryan Maue? Paul Linsay? You may want to check this.
Bender–
Except when it’s not. 🙂
If we assume weather noise IS AR(1) and has the lag-1 correlation that gives the variability in 8 year trends Gavin gets, then you can prove the monthly weather data since 2001 is an outlier. By a lot. It’s just not variable enough. 🙂
I will bet that local ocean heat content fluctuations follow a scale-free power law distribution – 1/f noise, not white, nor red. Note this would be very different from surface temperature in the well-mixed atmosphere. I wonder if there are deep ocean temperature yiime series for Iceland, at the top end of the THC. I have to say, I strongly support Pielke’s view that ocean heat content is a critical parameter worth studying. The historic focus on land surface temperature has to change.
AR(1), but probably not many AR(1)s summed, as
http://www.scholarpedia.org/article/1/f_noise
#105 Hey, I’m not dogmatic. Use an AR approximation to 1/f if you like. The details don’t matter. It’s the LTP that counts.
Re #105
It makes sense that using multiple AR(1) series summed can generate a realistic power spectrum for a time series. I think I would be wary of using that approach for significance testing, though, since it implies different assumptions about the frequencies much lower than the minimum resolvable frequency from the series (i.e., 1/t, where t is the series length). This may not have much effect on the look of the power spectrum, which has limited extent, but I suspect it could well have an effect on the apparent significance of a trend within the series.
This reminds me of the Schwartz and Scafetta example, discussed at Lucia’s place here. This relates to the “controversial” Schwartz paper which found a short time scale for climatic processes. Scafetta investigated and felt the data was based described by two different time scales. This would come as no surprise at all to Hurst fans, for the reasons described above.
To my mind, treating the problem in this way is possible, but the solution seems to have a degree of “cycles and epicycles” about it. My instinct is that generalising the scaling behaviour would be a better route to take. My instinct is not always correct though 🙂
4 Trackbacks
[…] this depends on whether climate is chaotic just like weather. Mandelbrot seems to have shown this: http://www.climateaudit.org/?p=396 I think the fact that many aspects of climate tend to display LTP / scale-free behavior is also […]
[…] there is no reason to assume that we can predict it any better than we can predict the weather. See Mandelbrot on the chaotic nature of […]
[…] there is no reason to assume that we can predict it any better than we can predict the weather. See Mandelbrot on the chaotic nature of […]
[…] obviously been intrigued by persistence issues for some time and have briefly discussed Mandelbrot and also Vit Klemeà’¦à⟼/a>, who has encouraged Koutsoyannis. In light of […]