One of the really annoying things about Wahl and Ammann was their failure to cite our prior analysis of various MBH permutations and, then, having failed to cite these prior analyses, reproaching us for supposedly “omitting” these analyses. For example, in MM05 (EE) we discussed the relative impact of using 2 or 5 covariance PC2 or using correlation PCs; we did so largely because these issues were already in play through our Nature correspondence and realclimate postings, where Mann had raised the same issues. (Wahl and Ammann don’t cite or even acknowledge Mann.)
However, when Wahl and Ammann carried out similar analyses, they did not refer to or reconcile to our prior analyses, leaving a highly distorted record. Here’s a graphic that I presented at KNMI, showing the virtual identity of MM05 (EE) results and Wahl and Ammann Scenario 5 results. (I spent several hours with Juckes coauthor Nanne Weber at KNMI and she did not inquire about this graphic.)
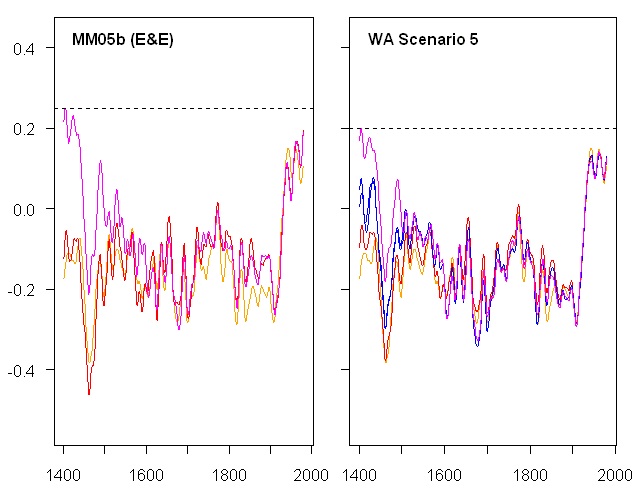
Left: Archived results from MM05 (EE) Figure 1. Orange- MBH98 as archived; red — MM05b emulation of MBH98; magenta — using 2 covariance PCs from NOAMER network. All smoothed. In addition, MM05b reported that 15th century results using correlation PCs were “about halfway” between the results with 2 covariance PCs and that “MNH-type” results occur if the network is expanded to 5 PCs. Right – WA benchmark and Scenario 5 cases using MBH98 weights and temperature PCs (after fully reconciling calculations to WA benchmark with no weights and WA version of temperature PCs). Orange — MBH98 as archived; red- WA benchmark varied as described; magenta — using two covariance PCs; blue — one graph with 4 covariance PCs; one graph with 2 correlation PCs.
The differences between the Wahl and Ammann emulation and the MM05b emulation are obviously very slight – apples and apples. The slight difference pertains to how the reconstructed temperature PCs were re-scaled. I discussed this on the blog in May 2005 after Wahl and Ammann released their code. Apples and apples, the reconstructed temperature PCs were identical in the two codes. The difference arises in the re-scaling procedure in MBH98, which is handled a little differently in the two algorithms, accounting for the slight differences. In MM05b, we calculated the NH composite using the reconstructed temperature PCs from the regression module without re-scaling; the resulting composite was then re-scaled to match the instrumental NH composite. In the WA implementation (which has been adopted in all fresh calculations reported here), the reconstructed RPCs were re-scaled to match the variance of the target RPCs. The WA source code acknowledge a pers. comm. from Mann in April 2005 for this step, which is undocumented. The practical effect of re-scaling prior to calculating the NH composite (as opposed to the other order) in this particular case is to cause a slight compression of scale and to improve the replication of MBH results. However, the replication, as noted above, remains incomplete and there is a disquieting remaining discrepancy in 15th century results.
The pink curve shows the emulation results using 2 covariance PCs in the NOAMER network, a situation illustrated in MM05b and discussed in Wahl and Ammann Scenario 5. The left panel shown here uses the identical digital information as the corresponding Figure in MM05 (EE), but is colored and smoothed differently to match Wahl and Ammann. The blue curves shown on the right shows the reconstruction using 2 correlation PCs or 5 covariance PCs. In MM05b, we reported the following result:
If the data are transformed as in MBH98, but the principal components are calculated on the covariance matrix, rather than directly on the de-centered data, the results move about halfway from MBH to MM. If the data are not transformed (MM), but the principal components are calculated on the correlation matrix rather than the covariance matrix, the results move part way from MM to MBH, with bristlecone pine data moving up from the PC4 to influence the PC2….
If a centered PC calculation on the North American network is carried out …., MBH-type results occur if the NOAMER network is expanded to 5 PCs in the AD1400 segment (as proposed in Mann et al., 2004b, 2004d). Specifically, MBH-type results occur as long as the PC4 is retained, while MM-type results occur in any combination which excludes the PC4.
The only amendment that I would make to the above comments is to concede a little less than conceded above: that inclusion of the covariance PC4 (the second paragraph of the quotation) merely moves the reconstruction about halfway from the results using 2 covariance PCs to the MBH results.
When you think of the various calumnies thrown out by Wahl and Ammann (and re-cycled by Juckes), the similarities between the results in MM05b and Wahl and Ammann Scenario 5 are remarkable. The failure of Ammann and Wahl to reconcile these results amounts in my opinion to a distortion of the research record, a distortion being perpetuated by Juckes et al.




6 Comments
Hi,
this is surely not the right article to make this request, but this one seems as good as any. Feel free to delete or move this to its appropriate place. My request is as follows:
Olavi Kàƒ⣲ner has done a lot of remarkable studies of negative versus positive feedbacks in climate. Reading his papers I find no fault in his methodology, but I am no statistics expert. Even so I find it puzzling that this work of his has not received any more attention as it is potentially a blockbuster. Then again… Anyways, his two main articles are On non-stationarity and anti-persistency in global temperature series and Some examples of negative feedback in the Earth climate system, both very interesting.
What I would like to see is 1) a comment from statistical experts here on ClimateAudit on the validity of this approach, 2) as a bonus an audit of the results.
At the moment I would be more than happy with just 1. If I understand the results of these papers correctly then a) the claim about positive versus negative climate feedbacks is not something that we need to wait far into the future to see unfolding, it can be measured now, using statistical techniques, and b) the result from the second paper implies that there are negative feedbacks in the climate system everywhere on Earth, but that they are weaker in the tropics. That in itself seems like a highly significant finding.
Comments?
Onar,
Although a little way off topic (SteveM, feel free to move this with the above post), this type of article is of great interest and although not specifically audited, these approaches have been discussed on this site:
The Mandelbrot and Wallis paper referenced by Olavi is discussed here.
Along similar lines, Cohn and Lins is discussed here.
I would also recommend reviewing some of Demetris Koutsoyiannis’ work, discussed here. Demetris has been on this site and has an impressive knowledge on these topics.
Suffice to say many of the people here are of the opinion that the statistical models commonly applied in climate science are not up to the job. ARIMA, FARIMA and FGN (fractional gaussian noise) being posited as much better models. Very little work seems to be done by mainstream climate scientists in this area.
Spence,
thanks for all these interesting references. Reading Benestad’s views was particularly illuminating.
It was shocking to discover that he really do believe that they understand climate very well, and that he is so impressed by the fact that climate models fit the data very quite well. (thereby revealing a thorough lack of understanding of the profound role of uncertainty in multivariable systems)
However, despite lots of interesting comments I am still at a loss about the physical interpretation of the Kàƒ⣲ner papers. Basically, he interprets the Hurst exponent as a measure of negative versus positive feedbacks in the system. A Hurst exponent between 0 and 0,5 implies non-stationary anti-persistence, whereas a Hurst exponent greater than 0,5 implies persistence. Kàƒ⣲ner finds H-values significantly lower than 0,5, implying anti-persistence and in his interpretation, negative feedbacks dominating the climate system. This seems logical, but I need to get a handle of what this means in practice. In particular, what would be extremely interesting to find out is what the Hurst exponent of climate models are. If Kàƒ⣲ner is correct in his analysis then it should be possible to test it right now: positive feedback dominated climate models should have a Hurst exponent > 0,5. If they do but reality has an exponent lower than 0,5 then this pretty much falsifies the whole thing, no?
Although, in order to put confidence into such a finding I would like to see the Hurst exponent calculated for a range of climate
sensitivites, all the way from a Lindzenesque 0,3 C/doubling to a doomsday 6 C/doubling. If Kàƒ⣲ner is correct, then a all climate models with a sensitivity lower than ~1 C/doubling should have a Hurst exponent lower than 0,5. ~1 C/doubling (i.e. zero overall feedbacks) should give H=0,5, and sensitivities 1-6 should give H>0,5.
Has anyone done this? If not, why the hell not? As far as I can tell it should be possible to use H to measure the climate sensitivity statistically by mapping the empirical value of H onto the climate model which best matches that value. Comments?
#3 Onar, I am confused by Kàƒ⣲ner’s finding of antipersistence, but I think that result is limited to short time frames and may be a consequence of easily explained periodicities (seasonality, e.g.) in the physical processes. However, as a general rule it is not always easy to find a good physical explanation for persistence of anti-persistence. In particular, long-term persistence (LTP) has been the subject of debate since its discovery by Hurst [1951] (see Mandelbrot; Klemes; Koutsoyiannis). While I am convinced that the LTP we observe in virtually all long climatological records tells us something fundamental — likely about the nature of the physical processes — I am not sure precisely what.
In any case, I do not believe H is an indication of sensitivity. In particular, although I am intrigued by your statement:
I do not think it is correct.
Perhaps Koutsoyiannis or Kàƒ⣲ner himself might have a comment on this?
Interesting discussion of the different parameters and statistical models on David Stockwell’s ENM weblog here, includes some further useful references.
Anyone got anything to say about Juckes citing Wahl and Ammann 😉
I am thankful to Spence and TAC for pointing out my work and to Onar for asking my opinion (he sent an email).
With the risk of being monotonous, I will repeat here a few of my theses which are related to this discussion:
1. Records which seem to exhibit long range dependence (LRD) should not be handled with the ease of typical statistical processing. LDR implies dramatically increased uncertainty and classical statistics can yield quite misleading results if LRD is not taken into account in statistical estimations. This extends to derivative time series (e.g. by differencing) and to transformed statistics (e.g. power spectrum). In this respect short records of say 20 years do not provide sufficient information to study processes which might exhibit LRD. (See details in Koutsoyiannis, 2003, and Cohn and Lins, 2005).
2. Nonstationarity and stationarity are not properties of a time series but of a mathematical process that models the time series. In this respect it is not possible to infer nonstationarity or stationarity merely from data. Some reasoning is also needed about (1) why a stationarity hypothesis cannot be valid for the process at hand; (2) what has caused the change of behaviour (in time); (3) whether this change is deterministically known (for instance a random change in the mean of a stationary model results in a composite model that is again stationary). (See details in Koutsoyiannis, 2006a).
3. The power spectrum is very helpful in detecting periodicities and choosing a cyclostationary against a stationary model (e.g. for monthly temperature). But it cannot be used to reveal whether a process without specific periodicities is stationary or nonstationary. Besides, it can lead to very misleading results in the presence of LRD. (I am preparing a paper about this — I hope to publish it in the next decade).
4. Asymptotic behaviours (e.g. the Hurst behaviour and the estimation of the Hurst exponent, the long distribution tails, the entropic dimensions) should not be detected in the “body” of a graph but in the appropriate “tail”. Otherwise (e.g. by neglecting the slope in the tail and taking an average slope in a graph with varying slopes), there is high risk to obtain mistaken results. (This I have demonstrated for entropic dimensions is an older paper that was published only recently: Koutsoyiannis, 2006b).
5. Obviously the climatic system is not characterized by a single feedback loop (e.g. a negative one, which perhaps would introduce anti-persistence); rather several feedback mechanisms, positive and negative, act simultaneously. I have tried to demonstrate that in a system with a positive and a negative feedback component whose parameters vary in time as if they obey some feedbacks themselves, the resulting time series can exhibit LRD even though the dynamics are fully deterministic ( Koutsoyiannis, 2006c).
From the difficulties I had to publish the above referenced papers and from what I see in the mainstream literature, I understand that there are not many who think that these theses are correct. So I am very grateful and happy that this blog discusses positively these ideas.
Now, coming to the papers that Onar brought into discussion, I leave it to the reader to decide whether or not these papers fall into some of the problems that I wrote into the above five points.