I have been spending some time (my wife would say “too much time”) examining how the Hansen Bias Method influences the temperature record. We have already observed that the Hansen method introduces an error in cases where the different versions are merely scribal variations. See http://www.climateaudit.org/?p=2019 and discussion.
The cause of the error has also been pinned down: in the case where a scribal version has only two of three monthly temperature values in a quarter available, Hansen calculates the anomalies of the available two months. It is important to note that the anomalies are the difference between the month’s recorded value and the month’s average value for the period of scribal record. Hansen takes these anomalies, averages them, and then sets the estimate of the “missing” month’s anomaly equal to this average. The “missing” monthly temperature value is then estimated by adding the estimated anomaly to the scribal record’s mean for the month. This occurs even when there is a temperature value available for the missing month in another scribal record. From the two available monthly values and the third, estimated monthly value a quarterly average is calculated, followed by a calculation of the annual average from the quarterly averages. Finally, for the two scribal records that are being combined, Hansen averages the annual averages for the overlap period, and, if there is a difference between the two averages, determines that to be a bias of one version relative to another and adjusts the earlier version downwards (or upwards) by the amount of the bias.
While the method clearly will corrupt the data set, there doesn’t seem to be any reason why it would introduce a material bias in northern hemisphere or global trends. We’ve observed cases in which the method caused early values to be falsely increased (Gassim) and cases where the method caused early values to be falsely reduced (Praha), and one’s first instinct is that Hansen’s method would not affect any overall numbers. (Of course that was one’s initial impression of the impact of the “Y2K” error on the US network.)
However, that proves not to be the case, because of a “perfect storm” so characteristic of climate errors.
Hansen’s network outside the US has 2 main components: GHCN records, which all too often end in 1990 for non-US stations (USHCN records continue up to date); and 1502 MCDW stations (mainly airports). The MCDW reports started in January 1987 and continue to the present day.
In Siberia, to take an important case under discussion, the overlap between the MCDW record and GHCN record is typically 4 years – from January 1987 to December 1990 or so. Here’s where the next twist in the perfect storm comes in. Instead of calculating annual averages over a calendar year, Hansen calculates them over a “meteorological year” of Dec-Nov. While there may be a good reason for this choice, it has an important interaction with his “Bias Method”.
Even if the two versions are temperature-for-temperature identical in the overlap period, the MCDW series is “missing” the December 1986 value and the 1987 DJF quarter must be “estimated”. Now suppose that Jan-Feb 1987 are “cold” (in anomaly terms) relative to December 1986 (also in anomaly terms). As it happens, this seems to be the case over large parts of Asia (other areas will be examined on another occasion). The variations in Asian anomalies are very large. Let’s say that over large regions of Asia, the Dec 1986 anomaly was 2.5 deg C higher than the Jan-Feb 1987 anomaly. And let’s say that all other values are scribally equal.
Under Hansen’s system of comparing annual anomalies, this difference of 2.5 deg C will enter into the average of 4 years ( in effect being divided by 48 months) and then rounded up to a “bias” of 0.1 deg C. Since the MCDW version is “cold” relative to the prior GHCN version, the GHCN version extending to earlier values will be lowered by 0.1 deg C.
It looks like there may be a domino effect if there is more than one series involved, with the third series extending to (say) the 1930s. Hansen combines the first two series (so that the deduction of 0.1 deg C is included in this interim step.) When the early scribal version is compared to the “merged” version, the early scribal version now appears to be running “warm” relative to the adjusted version by 0.1 deg C. So it “needs” to be lowered as well.
The net effect is to artificially increase the upward slope in the overall temperature trend for most of the stations we have studied. As noted earlier, this process can bias records in the other direction, but stations with the requisite conditions have been hard to come by – Gassim being one of the few.
Update
To visually understand how the method works, I took the combined record for Erbogacen and corrupted it using the bias method. The data I use has already been processed through this method, but that is really unimportant. What is important is that I have a complete set of records that I can artificially split into two “scribal” versions. If the method for combining stations worked appropriately, the recombined record would be identical to the record I started with.
The first image shows the original record where I have defined two “scribal” versions that overlap in the period of 1987 through 1990:
The second image shows the result of estimating the DJF temperature for the latest scribal record, overlaying it with the older scribal record. As you can see, the estimated annual value falls below the actual value due entirely to the estimated DJF value.
The third image shows the impact of then using the bias method to recombine the two scribal records, using the estimated value for 1987 (derived from DJF) as input into the algorithm. This result is overlayed with the original record. As one can see, the bias method has “cooled” the early years of the original record.
The final image simply shows the trend lines for the original record and the recombined record. Clearly, the bias method has increased the apparent warming trend for this station.
Climate Audit 
90 Comments
John G:
Nice concise summary. Do you have a list of the Siberian stations you have examined? I continue to think the best way to gauge the potenital impact of Hansen’s assumptions is to look at where the results are most extreme, i.e., the Arctic and Central Asia.
I am so glad my maths is not up to the requirements of this site, or else I would never get any work done!
Keep up the good work….
John, could you or somebody illustrate this graphically step-by-step? Your explanation is clear, but there’s too much information for for my brain to pick through and get it precisely pictured.
Could you repeat the description using algebra? It would make it much easier to follow.
#3 Gary…I will try to create some graphics and post here.
#2 Andy
I began by looking at the following Siberian stations: Erbogacen, Bagdarin, and Kalakan. Unfortunately, they all are combinations of more than two scribal records. To reverse engineer the method I looked for stations with just two records. In this case I had to look outside Siberia and found (among others) Praha-Libus, Gassim, and Joensuu. Since then I have examined Barguzin, Bratsk, Cara, Jakutsk, Troickij Priisk, and Ust Barguzin.
So the ROW switches from GHCN records to MCDW records in the late 1980s, roughly the same time that the AGW movement gains momentum.
Coincidence?
#4 Paul: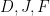
are the actual temperature values for the months of December (previous year), January and February (both current year), respectively; 
are the means for the respective months in the scribal record, and 
are the anomalies for each of the months.
OK, assume for the latest scribal record that
What I am saying in the post is that because the scribal record begins in January, 1987, our value for D is missing, so we need to estimate its anomaly and absolute value:
Now we use the estimated value for December to get an estimated value for the DJF quarter:
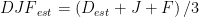
Which gives us an estimated value for the year:
The thesis is that for many, if not most, of the stations the annual estimate is less than the actual. This will cause the older scribal record to be biased downward when using the HL87 method of combining records.
One thing for a clarification/speculation: Hansen only estimates monthly temperatures implicitly. That is,
is equivalent to estimating the seasonal anomaly to be the average of the two monthly anomalies (that is, I think monthly values are never actually calculated).
Since the calculation of the annual averages is based on the seasonal averages, Hansen is able to “estimate” the annual average even when there are only six months of data available (one season missing completely; every other season missing a value). Additional strange consequence (with the caveat that I haven’t checked if this is actually somehow explicitly excluded): split a record into two in the following manner (letters denote months):
station1: DJ MA JJ SO
station2: JF AM JA ON
This should be combinable according to Hansen’s method with possibly a huge bias…
Finally, a request for all you C-wizards: at least my understanding of the procedure has been based on experiments. Now as the code is available, everything should be checked. The annual anomaly calculation seems to be located in monthlydata-folder of the EXTENSIONS-code (C-code under STEP1) and is called from the get_records-function (comb_records.py):
#9 Jean
You are correct. Hansen never goes back and fills in the estimated monthly values. Similarly, he never goes back and fills in the missing seasonal value when calculating the annual average when only three of the four seasons are present. Also you are correct in pointing out that he can calculate an annual average when as many as six months are missing!!!
John,
Let me congratulate you on some excellent CSI math detective work, and on also earning status to publish on CA. Steve is obviously impressed with your work, and rightly so.
It is very satisfying to see this turn into a team effort from many fronts.
Thanks, John. It will be interesting to see what happens when the relevant code is modified appropriately, rerun, and the results compared quantitatively.
#11 Anthony
Thanks. I’ve said it before and I will say it again, this kind of forum is great for problem-solving. Steve, as always, makes interesting observations and provides useful feedback both in this forum and via email. Also, Jean S. and KDT made comments in various posts on topics I had visited a while back but had not connected the dots. Those were true “Aha” moments when reading through what they had to say.
There is a consistent 3.0 to 4.0 C degree rise over the ’87 to ’90 time frame in Scandinavia that I noticed in other Siberian and Asian locations, though not with as high an increase.
I had assumed a solar cycle was the most significant cause of the spike, but it could be related to the MCDW change. It is much more than just a rounding error in any case.
I really that you guys will put all this work into a formal paper. I believe that this would bring much more clout and credibility (not that you don’t have any at the moment).
A formal peer-reviewed paper would have no reason to not be included in the next IPCC repor.
#15: How about a formal peer reviewed paper about the apparent problems with the formal peer-reviewed paper process? Or would this be an oxymoron? The paper should includes issues with scientific funding and political interference.
Is it possible to validate the intention of the method as well, and check to see if there is good correlation between the anomalies for adjacent months. I wonder if there is not a trend for one warm month to be likely to be followed by a cool one (or at least a less warm one). I’m fairly sure rainfall has a pattern like this (so the seasonal variation is less than the monthly variation, and less than the daily variation).
Geez, a guy goes away for a week and all hell breaks loose, Hansen releases his code, CA discovers many strange rounding, step, and scribal anomalies, everyone is talking, and I have to read through a 350+ thread plus a couple 100+ threads to get caught up. There certainly is a buzz in the air. Great work everyone.
Ian
PS: John, Paul is right, the algebra is easier to follow.
RE: Peer review. My past experience with the formal peer review process in the field of analytical chemistry was that the examination was relatively superficial as compared to the virtually constant peer review that the climateaudit.org research is subjected to. Unless Hansen or Mann are the reviewers, formal peer review shouldn’t be a problem?
John:
Neat graphics. But as you allude to in your opening statement the effect will be benign if the Dest is sometimes below and sometimes above the actual. The question therefore is the extent to which December 86 is unusually warm or cold on a local, regional and global basis. A parallel came up last week for Omaha in the 80s. One additional thing you have pointed out though is to track actual time of missing data. If it is not random across months and years, systematic biases can be inadvertently introduced into the data.
The monthly temperature of a loaction looks a bit like a skewed sine-wave. At each site it would be easy to workout the average monthly temperature and then findout what the line shape actually is. If you know the lineshape you could easily fit missing months to the lineshape of the yearly average line shape, fitted to known values. You could compare the two methods, Hansens missing months vs. calculated from lineshape.
I have every reason to believe the NET impact will be warming.
WHY. Very simply if you look at hansens exclusions ( stations dropped: crater lake;, time
periods dropped: early norcal) ALL of his EXCLUSIONS, exclude cold bias.
1.If his scribal combination method (SCM)Induced a noticable chilling HE would have found it.
2. If his SCM was NEUTRAL I’m a statistcal monkeys uncle. A bias mean of Zero is rarer than
a britney spears brain cell.
3. His SCM method ( I BET) leads to SOME warming bias. Which passes unnoticed because it confirms
his BIAS.
IN short, A Zero bias is damn near impossible. A cooling bias would get his attention a warming
Bias would pass unnoticed.
RE 21. Yup!
If you look at daily data or monthy data on a long enough time scale you will see the
periodic functions. And your mean temperature is like a DC bias. and your global warming
is a TREND in the DC bias.
Make sense?
RE 15.
I would rather see hansen fix the mistakes than see people here bogged down in the
years long process of getting something published in a journal no one reads.
Journals are an academic pissing contest.
John, thanks for the quick response on the graphics. Short, sweet, and to-the-point. Good job.
DocMartyn said:
I second that!
Ian
#8 – How did Hansen come up with the mean for December (previous year) if December (previous year) is missing?
John Goetz: A perfect example, well described and illustrated. The unconvinced are undoubtedly busy checking your analysis for themselves. How nice that they can do that, and satisfy their doubts! This is the way science is supposed to work. Nice job.
I would rather see Hansen, and all the warmers, admit that a global average or mean temperature is a meaningless metric. It doesn’t even rise to the level of apples and oranges.
#27
The mean for December is from the current scribal record. Therefore, the mean is calculated over 1987 – 2006 and is used in the implicit estimation of the Dec 1986 value.
RE 29.
Hansen has admitted as much and he does the anomaly dance.
#29
Here is the link to “The Elusive Absolute Surface Air Temperature (SAT)”
http://data.giss.nasa.gov/gistemp/abs_temp.html
The SAT was needed as a method of estimating global temperature change
for comparison with one-dimensional global climate models (according to GISS/Hansen)
So it still seems possible that Hansen will escape with a bloody nose,
and a few bruises. 😉
#24 “Journals are an academic pissing contest.”
Not if you’re an experimental scientist.
So, not only have we garbage models, we also have garbage in.
There is only one certain result … WE’RE ALL GOING TO DIE
… oh, sorry for the slip there….There is only one certain result, garbage out.
In all seriousness, what I see here is not elementary mistakes, but infantile reasoning. There must be several sound ways of dealing with disparate data sources, it’s not a new problem. But Hansen has simply gone off on his own ad hoc tangent. Was there no peer review?
Does the bias carry backwards to earlier data? Erbogacen seems to have data back to 1936 on GISS. If I understand GISS, they have 7 strings of data that have been merged. (One series, I guess, is just a few datapoints in 1913)
#36 nrk
Yes, I used Erbogacen for illustrative purposes only. In fact, because there are seven records that are combined for this station, the older data gets biased ever downward.
#35 nrk
A straightforward method of combining scribal records, in my mind, would be as follows:
1) Examine the overlap period month-by-month.
2) For monthly values that are identical, simply use that value in the new record
3) For monthly values that are not identical, simply use the average value in the new record
4) If a monthly value is missing from one record, but present in the other, use the value that is present in the new record
5) If the monthly value is missing from both records, record the new record as missing the monthly value.
Very impressive John Goetz, both that you found this and that you can explain it so I can understand it. Please pass on my appreciation to your wife for her sacrifice.
#38 John Goetz:
Your procedure for combining scribal variations will work, assuming you can identify scribal variations first. Here’s my idea for combining *any* overlapping records:
1. For all months with values in both records, calculate the difference between the records
(exclude any months with one or zero values when calculating differences)
2. Calculate the mean and standard deviation of the differences from 1
(variance should be used for quality control and for determining the overall uncertainty)
3. Apply the mean as an offset to the appropriate record
(if subtracting record 2 from record 1, apply the mean difference to record 2)
4. Continue in this way until all records have offsets applied
5. Merge all records by averaging all available values (with offsets) for any given month
(also combine the variances)
6. For missing months (ie. no record with value for a month), use another algorithm to estimate a value for the month (with appropriate variances)
I believe this algorithm will result in no offset being applied to scribal variations.
I also suspect that the order of combinining records has no effect.
Have I missed something, or would this work?
What’s Hansen’s rationale for using the anomalies to find the missing value (or is there not one)? Wouldn’t that tend to overestimate extreme anomalies because of regression to the mean?
38 That makes sense but even in 5) a value could be reasonably estimated from surrounding months and simply noted as an estimate. The lack of documentation, possibly due to limited computer resources (frightening thought), is ridiculous.
Your explanation of the combination does seem to explain the older series adjustments. I am still not convinced that there are not newer series adjustments that are not documented. If the data provided were truly raw, then it would be very simple to follow the combination. With most overlaps being identical other than the DJF average error, I find it difficult to trust the data. The scribal thing confuses me
Admittedly, I am not a scientist, I was just a Test and Balance Engineer that measured quite a few temperatures. Then I compared everything that could be compared to verify the validity of those measurements. If everything agreed to +/-5% I was golden and I was just checking HVAC equipment, not predicting a global climate change.
Digital thermometers whether thermocouple or thermistor were incredibly inaccurate in the late ’80’s. They could be tightly calibrated for a short term, but drifted so much that they required constant calibration verification. Around 1994 the accuracy improved to the point that I started having some trust in them but I still had a few hundred bucks worth of mercury thermometers around to double check the $500.00 digital equipment. Self heating was a major problem with the digital equipment back in the day.
While I doubt that most scientists would be unaware of the limitations of various generations of test equipment, other than a few at the University of Utah, there were problems with digital equipment in the ’87 to ’92 time frame.
The huge jump in temperatures in Scandinavian starting in 1987 that is evident in most Eurasian high latitudes during that time would freak me out if there were an instrumentation change taking place. Hell, it freaks me out anyway since the only game in town then was a strong solar cycle, since solar cycles have no temperature influence globally after 1980.
Forgive my uneducated opinion/rant but I think there is something rotten in Denmark.
John:
Okay so it looks like Dr. Hansenstein stitched together the GISS-TEMP monster and Im ready to light my torch and storm the castle with a rope. BUT, before I strike the match, is there any valid rationale for his methodology (I can think of some invalid ones like stretching the warming trend to make his models look better, but are there any valid ones)? It would be nice to hear it from the Dr. himself (or one of his proxies who sometimes lurk here, Gavin S. et al.) but I doubt that is going to happen and failing that, Id be interested in your thoughts.
I have another question born of my inadequacies in math. I know you indicated that there is good reason to think that a bias would be neutral but wouldnt his methodology tend to exaggerate any existing warming signal (say, recovery from LIA, urban heat bias trend or bias from poor station siting)? Last, I add my congratulations to the many well deserved others on the string.
#43 togger63:
I know your question was directed at John Goetz, but let me give my opinion anyways. I think he made a mistake in attempting to estimate missing monthly values, but there is nothing apparent in the algorithm that would skew the results either way. (We don’t even know the net effect of the algorihmic mistake yet).
With the benefit of hindsight, it is clear that the GISTEMP method of combining scribal variations is, uh, sub-optimal (to say the least). However, if you were attempting to combine records without thinking about scribal variations, how would you do it? You would have to compare months with multiple values and get the average difference between them to determine the offset.
To get more months for comparison, you may try to estimate a value for missing months. (That would be a mistake, but it *seems* reasonable). Remember, you are not thinking about scribal variations so you have to think of every record as an independent measurement. Therefore, you must make your estimate using only values from the current record. You can’t copy values from other records, because you think they are independent. So, given the task of estimating a value for a missing month using values only from the current record, the GISTEMP algorithm is quite good. (I would have averaged the anomalies from adjacent months instead of from the other months in the season, but it’s still pretty good).
Again, in hindsight it was a bad idea to estimate missing values for the purpose of calculating an offset. Doing so in the presence of scribal variations was a serious mistake. But I believe it was only a mistake.
re my post #40 above:
I want to retract step #6. There is no reason to estimate the value for a missing month. If a station has no value for a month, then it simply does not factor into any larger average calculations.
It may have been necessary in the 1980s to work with yearly averages for each station, but with modern computers we could easily work with monthly data (or daily data).
John V.:
Thanks. I think I see your point — the method is “good” at keeping each scribal version of the record independant but the manner in which it does it inadvertantly introduces bias, correct?
#46 togger63:
Statistically speaking, as I understand it, the bias *should* be neutral.
Of course, the bias will not be exactly zero. It could fall on either side of zero with 50% odds.
Re: 44 and 46
Interesting points, both of you. Very technical however. On the basis of these “mistakes” and “inadvertantly” introduced biases we now have a global body of politicians making decisions that will negatively affect the global economy, and in particular the developing societies around the globe, in order to fix a “man-made global” warming problem that by all best available accounts remains unproven.
That, in a nutshell, encapsulates the profound damage done by Hansen et. al. [with the IPCC standing in as the Wagnerian choir, as it were].
It seems to me, real difficulties arise when combining data where one or both sets are missing numbers. One way, of course, is to leave that value blank indicating the data is missing. The problem when doing this is that it affects the annual mean, which I think is important looking at the graphs above. If the missing data happens to be in a month like January or July, the average with missing data will skew the yearly mean considerably.
Perhaps a better way when data is missing is to find a polynomial that fits a selected set of points and assume that the polynomial and the function behave nearly the same over the interval in question. DocMartyn alluded to this above.
Spline fitting a curve is one such method, like the cubic spline, Bezier curves, or B-spline. A numerical method or technique of this type will generate a more reliable value than mere averaging with standard deviation and variance.
Ian
#49. No. There is no “bias” between scribal versions. It’s nothing to do with curve fitting.
#49.
The more I think about this, the more I realize there is no need to calculate the annual mean for a single station. The monthly mean for a region can be calculated every month using only the stations that have data for that month. The yearly mean can then be calculated from the monthly means. No estimates are required at any step.
This assumes that a substantial number of stations (with good spatial distribution) have values for every month.
Re # 40 JohnV
“Have I missed something?”
Opposite. You have put something in. You have created missing values. Simple question: Are there not enough data worldwide to do all required analyses by disregarding missing data? After all, missing data insertions are guesses.
BUT, it is very important to check the meta data for WHY they are missing, like Nagasaki 9 Aug 1945 or Darwin 25 Dec 1974 (cyclone Tracy destroyed the weather station) and so on. The dates just AFTER missing data might have anomalous data. It’s a process of understanding that I think would be hard to automate. Geoff.
#52:
I assume you are referring to step 6, which I later retracted (see post #45). It was only there for months with no data available, but I have since realized that it should never be necessary to estimate anything (as you said, and as I said in posts #45, #51).
Good point about anomalies after missing data.
Steve said,
Okay, but some have discussed combining scribal data and utilizing a simple first order interpolation to ferret out numbers between known values. I was referring to a situation where data is not available for one reason or another, in lieu of bad or missing data.
If as you say, there is no bias between scribal versions, there are certainly variations, would you agree that John Goetz #38 algorithm or John V. #40 algorithms is the right methodology?
Good job, John Goetz. I see that the difference between the biased and the original trend lines is around 0.1 degree. That means a fabricated increase (or hyperbole) of 0.1 degree.
#43 capdallas,
The big temperature jump in the 1980s is well observed by Swiss stations (I trust them for accuracy), and is undisputable in rural stations (like Saentis). Then there is a plateau so far. Both can be in no way explained by the GHG theory.
Hansen terminates many rural series data after 1990 even if data exist up until 2007 (that can be easily seen for France, with just 43 stations used by the GISS) so as a result, it masks the temperature plateau of the last decade shown by satellites, radio-sondes and even the CRU.
The uptrend has been made both ways by Hot Hansen: cool the past, heat the present.
Re #53 John V
TOB error with time lags in different parts of email world. I agree with your retraction of step 6. Apologies Geoff.
#40 John V.
I would agree with dropping #6, as I don’t like “filling in the blanks” as a step when combining records. Make it a step after all records have been combined. As for the remaining steps, adding offsets to the records (step #3) is the sort of thing that got us into this mess in the first place. I’m also not sure it would yield a better answer.
#43 Togger63 (and others)
I believe the use of the process to combine scribal records was derived from the method used to combine temperatures within a gridcell. Because I’m not one to believe in conspiracies, I’m sure it simply seemed like a good idea at the time and was simply an honest mistake.
#42 captdallas
I do believe there are other, undocumented adjustments going on in these records, although I would not necessarily point the finger in just one place. As an example, while I was studying this problem I observed something interesting with the scribal data for Bratsk.
Bratsk record 0 and record 1 overlap from 1951 through 1990. Looking at the period from 1951 to 1965, I see an interesting pattern of differences on a month-by-month basis. Subtracting record 0 from record 1, I see that most (not all) differences are as follows:
Jan – 0
Feb – 0
Mar – -0.2
Apr – 0
May – +0.2
Jun – +0.3
Jul – +0.2
Aug – +0.1
Sep – -0.1
Oct – 0
Nov – 0.1
Dec – 0.1
This pattern indicates to me it is more than a scribal error…it is an adjustment, and it warrants further investigation.
#60
I should add that after 1965, most of the monthly records have a difference of 0, and when differences occur there is no clear pattern.
#58 John Goetz:
Excuse me if I misunderstood your post, but some sort of offset method is required to combine independent records (not scribal variations) at a single station.
For example:
If a new thermometer is added but both old and new are maintained for a period of overlap, then there must be a way to combine the trends from both. It is likely that there will be a temperature bias between the two, so an offset is required.
(Incidentally, with a resolution of only 0.1C on the monthly means, the new and old thermometers may have nearly identical values — making the distinction between scribal variations and independent records difficult).
A quick question regarding scribal variations:
How do we know which records are scribal and which are just similar?
For example, if we don’t know that Bratsk record 0 and 1 are scribal, then the differences in Bratsk (post #60) could be explained by instrumental bias (instrument 1 reads high on cold days and low on warm days, relative to instrument 0).
#63 John V
That is a good question. I think Steve has commented in the past at the lack of a document trail specifying where records come from. In the specific case of Bratsk, my working assumption is that it is scribal because after 1965 the records largely match, whereas prior to that they differ as described above. Thus far this has proven to be a signature of an adjustment. However, I am glad you pointed out that it could be a difference in instrumentation. It is possible that an instrument change was made in 1965 such that both stations came into line. It will take some work to tease the reason from the record, if it is possible.
Note also for Bratsk that the negative readings occurred in March and September, and that positive readings occurred in not just the summer but also December and November. It feels scribal.
You’re right — I didn’t notice that.
FYI, I tried plotting the average vs the difference for the period 1951 to 1965, but there was no apparent pattern.
I like how it’s put in #22…I’ll replicate it as I understood it:
1. There is an erroneous trend caused by Hansen’s methods.
2. Such a trend is massively unlikely to be 0.
3. If the erroneous trend introduced cooling, Hansen would have found and corrected it.
So if there’s a non-0 trend that isn’t a cooling trend, it must be a warming trend 😉
Of course, while 1 is all but confirmed, 2 ‘could’ be wrong, and 3 relies on Hansen’s thoroughness and reliability as a scientist.
Haparanda has some interesting stuff happening in the 70’s early 80’s. The combined is as much as 0.15 degrees lower than two other series running at the same time. The rest is mainly the -0.1 adjustment until 1988 then no adjustment. Haparanda has four data sets combined. The -0.1 degree adjustment appears to be only due to the ’87 DJF averaging error.
s0 comb. s 2
1972 2.11 1.99 2.1
1973 2.52 2.53 2.76
1974 2.38 2.28 2.13
1975 3.13 2.98 3.09
1976 0.52 0.4 0.53
1977 0.76 0.62 0.73
1978 0.78 0.53 0.52
1979 0.24 0.15 0.32
1980 0.83 0.71 0.87
1981 0.13 0.02 0.14
1982 0.97 0.84 0.97
1983 1.95 1.82 1.95
sorry my table got scrunched, the center column is the combined.
#60 John, I haven’t looked at Bratsk but it sounds like some other old records I’ve looked at. For those, my guess was that the different versions were each estimated off of the same hand-drawn graph or chart. This explained the variations better than if they were copies of numerical lists with ambiguous handwriting, which has a much different pattern. They could also have been separate records but not very likely. Maybe Bratsk is another example.
#67: Haparanda also combines perfectly with my code. I also run the combination code but using the calendar annual mean estimation: in this case the Hansen’s December gift (Dec bug) causes pre 1990 data to run 0.1C higher than with the calendar year estimated combination. In Bratsk, for example, the effect is opposite.
Follow-up on #69: A signature of dual estimations from graphs is the presence of a specific kind of error in the negative temperatures. A good example is a graph point of -9.2 which is entered as -10.8 when the transcriber reads the chart upwards instead of downwards.
70 The gift is pretty random. If I get a chance I am going to spend more time on 1987 overlaps only. I just can’t shake the feeling there is something there.
I experimented with the 41 Russian (country=222) “rural” sites to see what their adjustments were in the first combining phase. There were both positive and negative adjustments, but there were more negative adjustments and there was an overall bias towards an increased trend in the rural sites – which then imprint the overall trends if Hansen has correctly described his “urban” adjustment. I haven’t estimated the overall impact, but it could be as high as 0.1 deg C. I think that it will be a bit like the Y2K error in that while it doesn’t look like there’s any reason for a net impact on the face of it, there will be a net impact when the sharp accounting is finished.
#60 John,
So I did look at Bratsk and that pattern is odd. Here’s an wild guess.
The original record is a list of 52 1-week averages. The two versions we have are each the original numbers converted into monthly averages. The cyclical difference between the two versions results from different methods of turning weekly averages into monthly averages. Maybe one interpolates and the other curve-fits. More likely, one uses 30-day months and the other uses proper months. I call this the irregular interpolation interval idea.
#74 KDT
Interesting idea, but I think practically it is more likely daily averages than one-week averages. I also really doubt curve-fitting is being done in creation of the scribal record. But frankly, who really knows? I have not really begun looking into it, but thought it might be worth throwing out there as an oddity. When I do get a chance to look at it, the first thing I will do is look for other stations with a similar oddity and see if there is any pattern across stations.
Follow-up to #75. I try to look for something simple. I believe the answer here will be simple, although finding it might be complex.
Steve:
If Hansen uses “rural” stations to correct urban stations upto 1200KM away, I assume that it is possible for “extreme” rural stations to influence large numbers of urban stations. It seems that making up for a lack of proximate rural stations is a major problem and leads or should lead, as in the case of Brazil, to essentially gray areas on the map. Were you able to verify that the 41 rural sites were in fact rural and not emerging urban locations? If you post the locations I will try to provide the latest population numbers. After all we know that Hansen’s population data can be somewhat misleading.
70 BTW, the variations between the s0 and s2 data sets mentioned in 67 are more representative real world comparisons of duplicate sites with separate instrumentation. If you look at the 1987 plus comparisons there is little variation in the overlap. So the same instrumentation was used (a BS series was created)or something was adjusted to produce magic. In any case the December gift is just plain nuts.
#78 I’ve noticed a similar jump in the figures for the GISS UK stations (only about six for the whole UK?). I have been lurking long time on this blog and only saw this eyeballable step change recently. Apologies for not providing a link. Then seeing your Swiss stations have the same apparent step change I wonder, is this something already acknowledged on this site? Is it a technical problem already adjusted by the team? Or is it something very odd? Any chance of another thread on this?
captdallas2, your observations on digital thermometers seems to me to be potentially very important. I think it’s the way of this world that in the pursuit of “world’s best practice” newer technology replaces older regardless of whether it’s better or worse. And digital devices are always thought to be better because human judgement is reduced in getting the data. It’s also a matter of budgets. Not everyone will be able to afford to replace equipment at once, so it might take decades for “world’s best practice” to be followed everywhere. If digital thermometers tend to give higher readings (as I think you’re saying) that could be a significant contribution to apparent global average increases, as the new technology spreads.
re 66 yes thats it.
In Hansen 2001, for example, Hansen excised 5 nrthern california sites that had a cooling
trend. The overall cooling was .01C. Cool be gone.
So if his methd here had a cooling bias he would find it.
And it is highly unlikely the bias would be 0.
Therefore I predict the Bias will be a warming one
re 77
The Rural adjustment uses a different range. It uses 1000km.
oh and the test for 1000km doesnt care if it crosses a big body of water
The Leba site (635121200002)is very interesting. If you compare the 1987 – 1989 monthlies you will see the same stuff I saw the first time we set up a A to D converter to run a month long test of a shopping mall air conditioning system. (Then the boss cheaped out with 2% resistors instead of precisions.) Without the daily values it is impossible to determine what happened, but there are some strange values to average.
#83 captdallas2
You can try to find daily values at one of the sites Steve links to here:
http://www.climateaudit.org/?page_id=1686
Try GHCN daily and Russian METEO daily
Demesure September 11th, 2007 at 2:27 am,
The uptrend has been made both ways by Hot Hansen: cool the past, heat the present.
That would be cool the past, heat the immediate past, ignore the present.
John V. September 11th, 2007 at 7:55 am,
Excuse me if I misunderstood your post, but some sort of offset method is required to combine independent records (not scribal variations) at a single station.
You have to allow for the possibility of not just offset differences but also gain differences.
Glass thermometers can suffer bore variations and electronics gain can vary with circuit output with even mW differences in resistance in the measuring circuit. The gain bias may not be random if the resistors used in a given design came from the same mfg. batch.
Thermistor heating can introduce another variable bias depending on temp, wind speed, and RH.
A lot of this could be fixed with high precision resistor networks. They cost more than $.01 per resistor.
That should be:
even mW differences in resistor dissipation
#85 M. Simon
Note that what prompted the quote “Excuse me if I misunderstood your post, but some sort of offset method is required to combine independent records (not scribal variations) at a single station.” was an odd pattern I observed in the differences between two scribal records for Bratsk from 1951 to 1965. I really don’t think the Russians at this particular station were using a digital thermometer at that time.
84 I may have to leave the dailies to the pros, that is a ton of data! I did find the 1989 daily but it doesn’t match the any of the Leba sets from GISS, close but not quite. Then I had to calculate Tmean from the Tmax and Tmin so it was a waste of time.
Sorry I got on the digital track, I still haven’t found out what if any instrumentation changes were made in 1987.
Okay, the daily averages I calculated are correct. They just don’t match the GISS averages due to 1) an obvious 2 degree scribal error in Aug series 2 data, 2)Major inconsistancy in the series 0 data set due to apparent instrumentation error and 3)an unknown positive winter temperature bias in series 1 and 2.
Other than that the record is just fine.
Leba series JAN FEB MAR APR MAY JUN JUL AUG SEP OCT NOV DEC
series 0 1989 1.4 4.1 8.7 10.4 12.3 16.5 20.3 17.9 14.8 9.4 2.8 1
series 1 1989 3.4 4.3 5.4 7.5 11.1 14.1 16.9 16.4 14.4 10.9 4.2 2
series 2 1989 3.4 4.3 5.4 7.5 11.1 14.1 16.9 14.4 14.4 10.9 4.2 2
combined 1989 2.5 4 6.3 8.2 11.3 14.7 17.8 16 14.3 10.2 3.5 1.4
from daily 2.9 4.2 5.5 7.5 10.7 13.8 16.4 16.3 14.3 10.6 4.1 1.7
0,1,2 mean 2.7 4.2 6.5 8.5 11.5 14.9 18.0 16.2 14.5 10.4 3.7 1.7
Here is one site that is interesting, but not in Siberia, Everglades Florida.
1) the gisstemp shows a warming trend.
2) the co2science site shows a cooling trend (same data set?)
3) the monthly download from giss indicated bad months.
4) the daily data from ghcn has bad days every where, so bad I would not attempt to run a monthlies from that data.