I’ve adopted a graphic from the R-gallery to better illustrate the issues that we’re working on with the Mann proxy correlations. I think that this should help.

Figure 1. Scatter plot of calculated gridcell correlations to Mann SI correlations, color coded by “proxy” class, together with marginal histograms. The dotted red lines show r=0.14, a 95% benchmark according to Mann et al SI.
This graphic shows several important data analysis points.
First and most importantly, the SI correlations are not random by “proxy” class, but are highly stratified. There are marked differences in average correlation for each of the three main classes (Luterbacher, Briffa MXD and ring widths). The Luterbacher series (article here; SI here) have very high correlations, but they are not really “proxies” as they use instrumental information to reconstruct European gridded temperature back to AD1500. Luterbacher states:
This reconstruction is based on a comprehensive data set that includes a large number of homogenized and quality-checked instrumental data series, a number of reconstructed sea-ice and temperature indices derived from documentary records for earlier centuries, and a few seasonally resolved proxy temperature reconstructions from Greenland ice cores and tree rings from Scandinavia and Siberia (fig. S1 and tables S1 and S2).
Examination of his SI shows clearly that the post-1850 Luterbacher series rely almost totally on instrumental data and thus, a high correlation to CRU instrumental data is hardly remarkable or representative of the ability of “proxy” networks without instrumental data e.g. the proxies available for MWP comparison.
The Briffa MXD series form a second stratification, also with very high correlations. This data set has been discussed on a number of occasions as they are the type case for divergence. In this case, Mann has deleted post-1960 values and substituted RegEM values prior to calculating the correlations. This can hardly be considered representative of other proxies. Re-doing the analysis with original data is currently impossible as Mann deleted the post-1960 values from the “original” data as well and the “original” data, originating from another RegEM publication by Mann and associates (Rutherford et al 2005) has never been archived (despite representations to the contrary.)
The bulk of the proxy series (red) are tree ring width series. Here the Mannian distribution of correlations has a bimodal distribution not present in the gridcell correlations. The Mann et al SI mentions a highly unusual procedure (which I called ‘pick two daily keno’ in an early post. Pick Three Daily Keno is a lottery in Ontario.) Instead of using the correlation to the actual gridcell, Mann calculates the correlation to the two nearest gridcells in his network. I am presently unable to fully replicate this calculation, but can do so for many series. (My guess is that there is some difference between the instrumental version used in rtable calculations and the version archived with WDCP, but these things are always difficult to sort out in Mann articles.) I’ve done some experiments with random data and simply picking the value with the highest absolute value from two random data points will introduce a bifurcation in the distribution.
The pick two procedure has another interesting result: as you can see, there are a lot of ring width series that fail the Mannian correlation test to the actual gridcell, but are bumped into “significance” by the pick two daily keno procedure. (Note: compare this graphic to the plot of random white noise in Comment #15 below.)
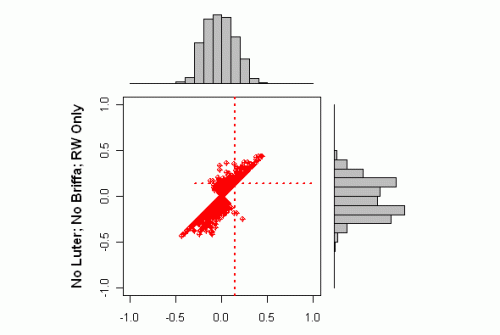
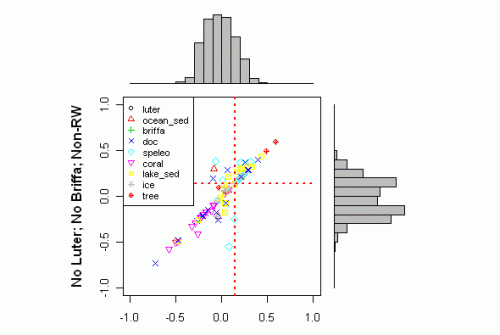
The handling of autocorrelation is another issue entirely. The dotted benchmarks here assume i.i.d. distributions, while actual series contain highly varying degrees of autocorrelation. Mann asserts that there is “modest” autocorrelation, but this assertion is untrue for many series. The “minor” proxy classes e.g. ice cores, sediments, do not show clearly in the above series and will need some further analysis. These proxies typically have enormous autocorrelation and autocorrelation benchmarks derived from tree rings have no bearing on their analysis, which I’ll get to on another occasion.
I’ve managed to replicate Mann’s correlations in R for the vast majority of series as shown in the graphic below comparing my emulation to the archived rtable values. Given the exact replication of so many series, the inability to replicate the other results remains a bit of a puzzle, but I’m hopeful of getting a precise reconciliation so that analysis is clarified. The difference between this graph and the top one is that both scatters incorporate pick-two methods.
Sept 25.
Here are a couple more versions in which I stratify RW series by themselves (excluding Luter, Briffa MXD and the odds and ends – ice cores, sediments, corals,…). This very much has the appearance of simply random data with some autocorrelation spreading out the distribution of correlation coefficients. Looks a lot like the random data in Comment #15.
Next here is a plot of the odds-and-ends. Over and above the issues shown in this graphic, there is another shoe to drop. The SI values for many of these proxies are different from the rtable values. This difference comes from another ad hoc procedure applied to some, but not all, of these proxies: “low frequency” correlation. Matt Briggs has written recently on this (see his recent post on smoothing). I haven’t assessed this little bag of snakes yet. I’ve examined autocorrelations on many of the odds-and-ends proxies and they tend to be very large, much larger than allowed for in Mann’s rule of thumb/





34 Comments
I tried to get the R script in the other post on this subject to run because I thought it would be a good project for me to work on correlating not just to adjacent temp gridcells but the whole thing. To see if perhaps an error was made in lat long. I kept getting errors saying unexpected “;” right before the load statement in the download data lines.
The pick two helped more than I guessed it would.
#1. Try again. I re-uploaded. I had an extra bracket in the script that I’d removed at the console.
What was the reason given by Mann for deleting the post-1960 Briffa MXD series?
#4
Translation – The data didn’t fit too good.
It’s one of the highlights for me.
Re: Jeff Id (#5),
Amazing!
It didn’t ‘work’ after 1960 but it was a good proxy before that.
What were the journal referees doing? So much for peer review……
What they don’t seem to realize is that if you have solid evidence that a proxy “loses sensitivity” for any length of time, you must assume that it “loses sensitivity” arbitrarily over all time. In other words, it ain’t representing what you think it is.
Mark
I am not a statistician, but doesn’t the lack of any points above the datum line in the lower left quadrant and the lack of data points below the datum line in the upper right quadrant just scream out “selected data”?
Re: David Jay (#7),
The fact there are few points in the left or right quadrants is not so much cherry-picking as automatically having two bites of the cherry. It comes from the trivial mathematical result: x<=max(x,y)
If Steve could replicate the data and data handling precisely then there would be no points in the left and right quadrants, and at least half the points would lie on the leading diagonal (/) of the X.
Re. 5 & 6
This is one of the (several) things that flabbergasts me about their papers. How can any semi-reasonable, self-respecting scientist give this sort of thing a pass? Dr. North?
#9. This particular is not one where people were “asleep”. It was an issue in IPCC AR4 where I objected to the deletion of the post-1960 values of the Briffa reconstruction. The only response was that it was “inappropriate”. David Holland has been trying for a year to get the Review Editor comments on this absurd response, only to be told by the Hadley Center that John Mitchell had destroyed all his IPCC correspondence and then that the correspondence was “personal” and not FOI producible.
What did you do to bring the correlations into so much better agreement? Was it just accounting for the the max(a,b)? Any other adjustments?
What would happen if one picked the max(a,b,c)? It should bring in fewer and fewer changes with each additional grid is added, but the distribution will become more and more bimodal. But with each addition, the significance of any particular cut-off will go down. Are there statistics on this relationship?
Please clarify, the comment above does not quite make sense – fascinating to read, I’m here everyday! Keep up the great work.
Re: Rejean Gagnon (#13),
Say, Rejean, you aren’t the same fellow who has worked on the Gaspe cedars, are you? On the off-chance you are, what do you think would be the possibility of posting some of those data here? Merci en avance.
The “pick two” procedure is described in the SI as follows:
The top graphic compares “pick one” correlations to “pick two” correlations. You can simulate this easily as I did a couple of posts ago. Make two columns of random numbers; from each row, pick the number with the highest absolute value; then do a histogram. It comes out bimodal.
If you do a plot of the first column against the “absmax” of the two columns, you get a scatter plot that has the same sort of look as the actual Mann results.
So I think that one can safely conclude that using pick two methods has changed the properties of the distribution and that tests based on pick one cannot be correct. The impact appears to be strongest on low correlation tree ring networks. The Luterbacher network (already instrumental) is highly tailored to the gridcell and hence pick two is irrelevant. But it makes a difference in the low correlation ring width data set.
The lower graphic illustrates my implementation of the pick two method versus the archived results. There are still some nits in my emulation pertaining to how the two sites are picked, but they are small nits and do not affect 99% of the picks. The nits pertain to two cases: (1) gridded “proxies” where the proxy is co-located with the center of a grid box and there is a tie between the east and west neighbors. Jean S observed that his code seems to resolve the tie in favor of the series with the lower column number. Since the columns are big hand N to S, minute hand dateline to dateline going East, I resolved ties in favor of the west neighbor. Most of the discrepancies show values for the east neighbor. At some point, I’ll test to see whether resolving in favor of the east neighbor improves the fit, but my guess is that it will end up being about the same with a bunch of west neighbor fits showing up. (2) Arctic sites where his algorithm finds a different neighbor than mine. I wouldn’t bet the farm on either algorithm right now for pole-crossing distances. It’s a small issue but I’ll come back to it some time. In either event, there seems to be a certain randomness in which pick two is done.
The bottom line is that the “pick two” method has implications for “significance” benchmarks. USing this method without changing the benchmark enables Mann to push quite a few low correlation series from below his benchmark to above his benchmark. Exacerbating the matter is that the assumed autocorrelation used to establish the benchmark in the first place appears to be severely under-estimated, a topic that I’ll return to.
The net result is that we’re probably going to end up with a rather pretty jujitsu demonstration of the randomness of Mann proxies using his own data.
Re: Steve McIntyre (#15),
Steve,
I can’t see your point here with respect to reconstruction. There’s red noise series that – even after undergoing post-1960 plastic surgery – still don’t look very hockey-stickish.
By second chance qualification few of them now are relabeled as carrying a small temperature signal and become included in the reconstruction – thereby spoiling any common signal Mann could hope to find. It just doesn’t make sense to me.
Notice another interesting aspect to the “topology” of the scatter plot of the random pick two (shared with the Mann graphic). There are somewhat prolonged prongs on the x=y line on both the positive and negative quadrants. This reflects the fact that, if you got a high absolute value correlation in your first pick, you were very unlikely to do better in your second pick. Pretty.
Re: Steve McIntyre (#16),
Steve,
I thought I had noted that earlier (#10). It would be interesting to know what proportion of your points lie on the y=x line, i.e. how many have better correlation with the gridcell they are nearest than with the second nearest. Just a guess, but I would not be surprised if it was about 60%. I would be surprised if it was less than 50%.
Steve: Your surmise isn’t too bad. Wouldn’t it would be surprising if it was less than 50%? It isn’t, but it’s not as high as 60% either. With Luterbacher in, it’s about 57% and without Luter about 55%. The effect is strongest in tree ring width data where the correlations tend to be low.
Re: Henry (#17), Steve’s response
So (ignoring series which are based on the local temperature) about 45% of the proxy series are more correlated with the second closest gridcell temperature record than with the closest. This does suggest that the local temperature signal is generally weak.
But it could be a way to demonstrate teleconnection, by refusing to stop at “pick two”: instead compare each series with every gridcell (big calculation, but even so) to find where in the world it is most correlated with. For the vast majority, it will be somewhere far away, thus proving teleconnection. And in most cases the largest positive value will be way over Mann’s filter, so most of the series can then justifiably be included in the next step of the reconstruction.
bender (#14):
Sorry, not the same person. Gagnon is a very common name in Quebec. The most common, I believe, after Tremblay. I am an engineer (not quite officially, but by training).
R
If you look at the big population, there’s not much HS-ness in it. But there wasn’t in MBH either. All you need is a few HS series oriented the same way and hundreds of white noise and low order red noise series and you can “get” a HS. In this case, the Finnish sediments and bristlecones appear to be carrying the HS.
Re: Steve McIntyre (#20),
Steve,
according to #17 an additional ~ 10% of trash proxies will pass due to the second-chance test. Simply lowering the bar a little would lead to the same result. At present I don’t think there’s much behind that part despite the affirmation that ‘treerings do work as proxies’.
From what I read in your #20 the basic procedure hasn’t moved on very much. Then I’m all with you that these alibroxies won’t carry much weight anyway – the algorithm will cling to series with distinct recent upticks. If it’s these contaminated finnish lake and bristlecone series, that needs to be demonstrated.
Steve —
It looks like you have a great letter to PNAS developing here! Please bear in mind that PNAS has a 3-month deadline for submitting letters and comments — after that time, all PNAS errors are exempt from correction! I found this out in my critique of the irroproducible results in Thompson’s 2006 paper, which will soon be coming out in EE instead, with discussion here.
Although PNAS letters are severely restricted in length, they can just summarize the conclusions of a thorough online SI, whose URL is part of the letter.
The Sept. 25 first figure above, for TR widths, is particularly interesting. How many observations are there, and how many have a positive own-cell correlation? It looks like this might actually be a minority, even though Mann uses a 1-tailed critical value (upper tail) on these series. In any event, I doubt that there is a significant majority that are positive (a presupposition-free 2-tailed test would be appropriate for this question).
I am puzzled by the fact that the Sept. 25 first figure has several prominent points on the back-diagonal (\) of the “X”. For these points, the near-cell correlation is almost the negative of the own-cell correlation. Your simulation in #15 shows that this can happen occasionally when the own-cell correlation is weak and there is zero correlation between the own and near cells, but even then there is no mode on the back-diagonal. Is there some kind of error here?
Re Bob KC (#8), I don’t know who the reviewers were, but note that it was NAS-member Lonnie Thompson who initially recommended this paper to the editors. It evidently met his standards of documentation and replicability.
Re: Hu McCulloch (#21),
Any idea which NAS member invited:
Ramanathan, V. and Y. Feng, 2008: On avoiding dangerous anthropogenic interference with the climate system: Formidable challenges ahead, PNAS, 105, 14245-14250, Sept 23, 2008.
… currently under review at ClimateScience under:
Misconception And Oversimplification Of the Concept Of Global Warming By V. Ramanthan and Y. Feng.
The autocorrelation properties of the Mannian series have every possibility under the sun and my guess is that the explanation is there.
From a statistical point of view, the properties of the data set are more and more bizarre as you look at it.
If I understand what’s going on here… the pick two method doubles your chance of significance. Suppose you have 100 pairs of random numbers and you compute 100 squared correlations. Depending on the amount of autocorrelation you might get an outcome just like generating 100 uniform random numbers between 0 and 1. If your cut-off for significance is 0.9, then 10% will look significant just by accident. But now generate 10 such columns of squared correlations, and in each row pick the maximum. We would expect this new list of numbers to be uniformly distributed between 0.9 and 1. Voila, 100 significant scores.
But I think there’s also an issue that the pick-2 procedure drops the coefficient straight down to the diagonal, whereas the confidence region is an ellipsoid, so some numbers inside the ellipse get bumped outside it.
Re. 21
Point taken. Still has a large flabbergast factor, though.
#24. There are a couple of aspects to this. These things won’t “matter” in the sense that they aren’t carriers of the recessive HS gene. But they matter a lot in terms of getting to the vote count of 484 votes for “significance”. My guess is that there might well be 100 votes here that shouldn’t count under the stated rule. While lowering the bar might get more in as well, it might not get the same ones in.
This is a very odd procedure that I’ve never seen in any previous statistics. My experience with the authors is that you can’t exclude the possibility that the odd procedure was done for a reason and that a non-odd calculation was done but not reported.
Ross, for the 90th percentile or 95th percentile, it looks to me like pick two is more like a few points from say .14 to .17 (white), with higher for autocorrelation.
OK — a naive question here
Has anyone checked if there is any geographic significance to this procedure? If a proxy site is on the boundary between two geographic regions, is this procedure a means of finding which region ( i.e the grid cell which contains the region) is more representative of the proxy?
I have a feeling that this question is more a display of my ignorance of the issues than anything else but anyway.
My surmise is that it’s just data mining. If this procedure were a clue to climate behavior, then it should be described in a separate technical paper.
It is probably rather evident by now, but the Mann et al. temperature reconstruction papers down through the years invariably depend on statistics that in turn can be manipulated by what might be considered an a priori choice, but that without a goodly amount of objective reasons for the selection become very suspicious as being an indirect means of cherry picking.
This leads me to the question whether reviewers of climate science papers ever object to cherry picking and data mining, be it direct or indirect? Or do they merely look at the formal statistics and assume that one of a scientific mind is going to use an a priori criteria as indicated (before the fact) and for reasonably objective and technical reasons? It seems to me that a strategy of forcing your statistics into a subjective mode would provide cover with reviewers that might be looking for a reason (or an excuse) to make a favorable or at least neutral review and at the same time obtain some reasonably good (for a desired result) data mined answers.
Some of these statistics, with what I will call a subjective bent, are rather obvious to a layperson, but I am wondering whether anyone with a statistical background has made a comprehensive list of these suspicious statistics and methodologies in the Mann et al. reconstructions.
The case in Mann et al. (2008) of eliminating the Briffa series for the poorly rationalized claim of divergence seems to be made even more questionable by using RegEM to put it back into the reconstruction.
I am aware that the RegEM (regularized expectation maximization) algorithm is a rather commonly used method for infilling missing data. My question as a layperson is, that since I have read that ridge regression is, or can be, a part of this method and that ridge regression in turn depends on a ridge parameter which is an extra parameter that has to be introduced in the model and its value is assigned by the analyst, and determines how much ridge regression departs from LS regression, can the RegEM method be made subjective?
Re: Kenneth Fritsch (#30),
Obviously I meant eliminating only part of the series or truncating it and not eliminating the whole series. Actually eliminating the whole series would have been the more honest choice here, although that might be considered a choice made to avoid a discussion of “divergence”.
ACtually I don’t think that much turns on the RegEM stuff. I think that some of these things are like the complicated distractions carried out by a magician. IF you have red noise (and this stuff sure looks noisy), and (1) orient the 20th century results by correlation to a trend; (2) eliminate those with a “negative” trend, you’ll get a HS as the pciking criterion wears off and you end up with cancelling noise in the blade. They are all variations on a theme.
There’s a VERY simple way to look at ridge regression. Stone and Brooks 1990 (Which I think that I’ve written about) describe a one-parameter continuum between OLS and Partial Least Squares regression (these are the ridge). There are some systems for picking a stop along the way – Mann’s “objective” criterion, but it’s still going to be a “blend” of the two coefficient approaches.
The real issue is the one that we were discussing with Brown – “inconsistency”. I can’t imagine that Brown confidence intervals will be anything below floor-to-ceiling.
The funny thing about Mann using the Briffa truncation is that I’m pretty sure that, at one point, we laughingly considered what would happen if Mannian end-point smoothing were combined with Briffa truncation. It’s hard to imagine that something even wilder has happened.