An interesting comment on Hegerl et al by James Annan here.
-
Tip Jar
-
Pages
-
Categories
-
Articles
-
Blogroll
- Accuweather Blogs
- Andrew Revkin
- Anthony Watts
- Bishop Hill
- Bob Tisdale
- Dan Hughes
- David Stockwell
- Icecap
- Idsos
- James Annan
- Jeff Id
- Josh Halpern
- Judith Curry
- Keith Kloor
- Klimazweibel
- Lubos Motl
- Lucia's Blackboard
- Matt Briggs
- NASA GISS
- Nature Blogs
- RealClimate
- Roger Pielke Jr
- Roger Pielke Sr
- Roman M
- Science of Doom
- Tamino
- Warwick Hughes
- Watts Up With That
- William Connolley
- WordPress.com
- World Climate Report
-
Favorite posts
-
Links
-
Weblogs and resources
-
Archives




36 Comments
Wow.
I don’t think I’ll trust anything from Nature again…not until significant changes are obviously made.
Hwang Woo-suk was indicted on charges of fraud and embezzlement related to his cloning research today. Prosecutors confirmed that former Seoul National University veterinary professor Hwang Woo-suk fabricated data for his now discredited research papers that claimed to have cloned human stem cells. A Fox New report said he could get life in prison for this fraud.
What is the penalty for dendro climate research fraud? How many years? Governments are spending billions reducing greenhouse gases, based on data and analysis that cannot be verified. Is this fraud worthy of a criminal investigation?
That is so spot on in so many areas. Thanks for pointing it out. I might also add that what people think, say and publish are not always in sync, to put it nicely.
My comments about the climate sensitivity and this story are here:
http://motls.blogspot.com/2006/05/climate-sensitivity-and-editorial.html
Bizarre reasoning.
re:#5
Isn’t it, just? James Annan had better be careful, lest he be tarred with the adjective of “skepticism”. Who knows where that might lead?
It might be useful here to distinguish fraud from incompetence.
Fraud is wilful misrepresention of fact while incompetence is ignorant representation of data as fact.
So in terms of climate sensitivity, which is aprioristically defined as the increase in global temperature from a doubling of CO2 concentration, that definition is not derived from experiment, and hence, as Annan et al did, honestly I must add publish, is a guess. The problem is that it can’t be tested using the normal standards of science.
So I suspect Annan has realised the issues associated with the definition of climate sensitivity and taken a step to disassociate himself from the flak that inevitably follows from detailed analysis of problematic theory.
Lubos,
you state that
Whereas Arrhenius and Myhre state
Which is valid in Modran up to 4000 ppm, can you explain the difference?
Dear Hans,
yes, I can explain the difference between the exponential and the logarithm. An exponential is a function that increases (or decreases) by a certain fixed multiplicative factor whenever you change the argument by an additive shift while the logarithm is the inverse function. 😉
More seriously, I can’t quite explain why and how the Arrhenius’ law was exactly used in your calculation because I don’t quite understand the application of this law. What I understand is how the Arrhenius law is used to calculate the temperature dependence of the rate of chemical reactions that needs some extra energy per molecule to run – energy that is obtained from thermal fluctuations that are governed by the Maxwell-Boltzmann factor.
I don’t know in what sense the greenhouse effect is a chemical reaction. You will have to explain your formula yourself.
What I can do instead is to explain mine. You take a dominant frequency at which the carbon dioxide absorbs. You realize that the infrared radiation at this frequency leaving the Earth that is not absorbed is a decreasing exponential function of the “thickness” of the carbon dioxide component of the atmosphere, which clearly gives the Ansatz T0(1-exp(-deltaConcentration/C0)). There is a maximum amount that the CO2 can absorb – namely all the radiation at the frequency or frequencies where it can absorb efficiently. This gives the saturation.
The main bug of this Ansatz is that the CO2 molecule absorbs at many frequencies and it has a quasicontinuous spectrum. When the concentration increases, one gradually opens new channels at which the absorption may occur. The formula above should be integrated over different frequencies with an appropriate weight, and the parameters of the integrand C0,T0 would depend on the frequencies. The resulting integral would have a different functional form, but it would still be true that the growth of the equilibrium temperature as a function of the concentration would be slowing down as the concentration increases. After all, this holds for your Arrhenius formula, too.
I hope that you will agree that I have justified my formula more thoroughly than you have justified yours, and now it’s your turn. 😉
Best
Lubos
Incidentally, “Modà…’„¢an” is a Czech word derived from the adjective “modràƒ⻢ which means “blue”. “Modà…’„¢any” is a part of Prague. My understanding of your comment about “Modran” is that you talk about “Modran 4” climate model but it seems that you don’t understand where the formula comes on physics grounds. (I know exactly how such a formula would be derived in chemistry but the relevance of this derivation for the greenhouse effect seems problematic.) Sorry but I will continue to prefer formulae whose physical justification and derivation are clear to me rather than obscure arguments based on climate black boxes from Praha-Modà…’„¢any. Hopefully it is OK to admit that the climate modellers in all groups should be ashamed if they’re using models whose behavior they don’t understand even at the level of the super-simplified no-feedback single-number calculation.
Re #9, Lubos
Sorry, I don’t understand this. Can you clarify ?
Dear Freddy,
the exponentially decreasing saturating formula is assuming that there is a universal value of the coefficient (that I wrote as “1/200”) in the exponent, which is only reasonable if you study the absorption at one frequency.
In reality, there are many frequencies that the CO2 can absorb. The frequencies that are most important for the calculations are those for which the percentage of absorbed radiation is comparable to 50% – neither too close to 0% not too close to 100%.
If you increase the concentration of CO2, the most important absorbed frequency will change, too. In the approximation where I approximate all frequencies by the most important one, I should still change the factor “1/200” in the exponent, as a function of the concentration. This would consequently change the functional form.
The kind of integrated formula I have in mind is
where “t” and “c0” are functions of the frequency. For appropriate choices of these functions, I can probably also make the full integral to behave as the Arrhenius logarithm, but right now I don’t know what the required functions are.
All the best
Lubos
Re:#11-12
Lubos was making a simplification that at any given time, only certain frequencies will both “have enough room left to absorb more” (not too close to 100% absorption) and be “increasing their absorption fast enough”[I think] (not too close to 0%) to significantly affect the near-term future. These are what he calls “channels.”
Of course, to do it properly, you need to integrate over all the channels, as Lubos noted in #9: “The formula above should be integrated over different frequencies with an appropriate weight, and the parameters of the integrand C0,T0 would depend on the frequencies.”
PS – according to Mathworld, “An ansatz is an assumed form for a mathematical statement that is not based on any underlying theory or principle.” Not sure if that’s the right nuance here, but then I’m new to the word.
As I understand it, Luboà…⟠is precisely right. Leaving aside Arrhenius, the logarithmic model is discussed in IPCC TAR at http://www.grida.no/climate/ipcc_tar/wg1/222.htm.
Actual absorption in a given wave length, as I understand it, is either in a linear range or saturated range, with the mix changing with concentration. The logarithm rule is an empirical rule of thumb (ansatz?) which describes the net result in ranges of interest, considering various isotopes, far bands, hot bands etc. , with the combination of changing linear and saturation effects being approximated by a logarithm.
More recent sources than Arrhenius for the logarithm rule are said to be:
Kiehl, J.T. and R.E. Dickinson, 1987 Study of the Radiative Effects of Enhanced Atmospheric CO2 and CH4 on Early Earth Surface Temperatures. J. Geophys. Res.92 2991-2998
Wigley, T.M.L., 1987, Relative Contributions of Different Trace Gases to the Greenhouse Effect. Climate Monitor 16 14-29.
Hansen, J., I. Fung, A. Lacis, D. Rind, S. Lebedeff, R. Ruedy, G. Russell, and P. Stone, 1988: Global climate changes as forecast by Goddard Institute for Space Studies 3-dimensional model. J. Geophys. Res., 93, 9341-9364.
One issue that intrigues me is the effect of water vapor overlaps. Clough and Iacono JGR 1995 have a detailed discussion of this using line-by-line models rather than the wider band models such as Modtran. Unfortunately Clough’s work was not discussed in IPCC TAR – an unfortunate oversight as the article seemed impressive to me and I’d be interested in how it stacked up.
re 9:
Lubos,
Arrhenius is known for two laws, one in electrochemistry (the one you are referring to) and one in greenhouse physics:
http://en.wikipedia.org/wiki/Svante_Arrhenius
I am using Modtran 3 (spelling error, but you cant edit postings here) Modtran 3 is online on http://geosci.uchicago.edu/~archer/cgimodels/radiation.html
As Co2 concentrations increase, the central band saturates, but the wings take over, keeping it nearly logarithmic. Here are some lab data of 1901 by Arrhenius in Germany

ref:
Arrhenius, S, 1901, Ueber die Wàƒ⣲meabsorption durch Kohlensàƒ⣵re, Annalen der Physik Bd 4. 1901, p690-705.
Here is a calculated EPA spectrum for 300 atm.m and 600 atm.m compared with a modtran standard atmosphere CO2 absorption:

correction: atm.cm
Dear Steve,
thanks for your references, clarifying words, and constructive approach.
Dear Hans,
it’s slightly entertaining how seriously you view the original 1896 Arrhenius paper (based on the just-discovered Stefan-Boltzmann law) given the fact that the first web pages found by “Arrhenius was wrong” are yours. 🙂 On these pages, you emphasize Arrhenius’ wrong Ansatz for the CO2 absorption spectrum.
http://www.google.com/search?q=%22Arrhenius+was+wrong%22
However, I don’t think that there is any real disagreement in between us. On the other hand, how much you trust that Modtran is doing the right job with these calculations?
Do we agree here that the no-feedback calculation is stable and the rate of temperature increase per 1 ppm of CO2 decreases as the CO2 concentration grows, instead of “exponentially” growing as some people argue?
All the best
Lubos
Yes we agree on that, also that no feedback sensitivity is 1K/2xCO2.
So we are back to debunking the scary economic SRES scenario’s, which is the specialization of Ian Castles.
PS http://www.google.com/search?q=Arrhenius+co2 The first four are mine 🙂
Re #12, 13, 14
Sorry chaps, I should have been clearer about my confusion. The sentence I quoted from Lubos’ #9 :
gives me a picture of CO2 absorbing all the radiation of a particular wavelength until it is pretty much “full”, then moving on to absorbing less “attractive” wavelengths.
This sounds wrong. Given that Lubos is a serious physics chap, I must be misunderstanding him.
Surely the result of a quantum of absorbable radiation hitting a molecule of CO2 is entirely independent of what is happening to the next molecule along, and of what has previously happened ?
I would expect that a chart of the proportion of a given wavelength that has not yet been absorbed, against altitude (i.e., amount of atmosphere it has passed through) would show an exponential decay, as Lubos says. I would also expect that different wavelengths have different probabilities of absorption, and hence different rates of decay.
What I don’t understand is why the amount of one wavelength that has been absorbed should have any effect on the amount of another wavelength that is getting absorbed.
Am I missing something about the basic physics of absorption here ?
Dear fFreddy,
when I read your text, I agree with everything you wrote. I am not claiming that the different frequencies are conspired in any way. Yes, they are independent.
I am just saying that if some frequencies are already almost fully absorbed, the amount of absorption no longer increases substantially when you increase the CO2 concentration.
On the other hand, given a certain concentration/thickness, there are other frequencies that are absorbed too slowly, and they are also not the most important one for the increase of temperatures.
In between these two extremes, there are frequencies that are not yet fully absorbed, but whose absorption rate is high enough, and these “marginal” frequencies are the most important ones for the increase.
It’s much like the Laffer curve argument about the maximization of tax revenue. 😉
The frequencies don’t look at each other what the other frequencies are doing. But they do look at the concentration and the absorption rate, and are absorbed depending on physical parameters. Each frequency interval, independently of others, contributes something to the equilibrium temperature. But I can still ask which frequency contributes most, for a given concentration, even though the calculations for each frequency are independent, can’t I? 😉
Concerning the statement that the derivative still decreases as the concentration grows – it’s because the total “delta T” is an integral of a function whose second derivative is negative (for every frequency) over frequencies, and therefore the second derivative of the integral with respect to the concentration is also negative.
All the best
Lubos
I might add that one thing which isn’t usually considered is that once you get to high altitudes where the absolute concentration of CO2 is much lower than at the surface, the ‘recently’ saturated frequencies will become unsaturated and additional IR will escape to space (over and above that escaping from ‘holes’ in the spectrum.) Thus, each cut in half of the atmospheric pressure will presumably result in a linear increase in atmospheric transparency.
Likewise since the altitude at which the atmosphere will have absorbed, say 90% of the IR from the surface at a given frequency, will be reduced as the CO2 concentration increases, this will change the structure of the total IR absorption and heating of the atmosphere. Of course the atmosphere is generally well mixed over relatively short time periods, so this is not generally too important.
re 15:
Here is a comparison of CO2 infrared absorption as postulated by arrhenius in 1896, as measured by arrenius in 1901 and calculated by modtran using modern spectra:

re: 21
The outgoing (more saturated) radiation wil come from an average higher and thus cooler layer. As infrared radiation is proportional to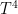 the total radiation will decrease.
the total radiation will decrease.
Re #20, Lubos, thank you, I was misunderstanding.
Re #21, Dave Dardinger
Dave, sorry, I’m confused again.
I thought that ‘saturated’ in this context meant that effectively all the radiation of a particular wavelength has been absorbed by this altitude. (Probably not the best word to use, I suspect.)
Does becoming unsaturated imply that new radiation is being generated at high altitude ?
Apologies in advance if I’m being ignorant again.
#24. fFreddy, Here’s what I find the most helpful way to look at the matter. The temperature of radiation-to-space from earth varies by wavelength. In the wavelengths of strong CO2 absorption, the radiation-to-space comes from the tropopause and is vey cold ~212 K; in the "window", radiation-to=space will come directly from the surface and is warm. A large amount of radiation-to-space comes from clouds or water vapor and is in between.
To the extent that there is more CO2 absorption due to more CO2, radiation-to-space will occur at higher altitudes. This is the position in Houghton’s text.
The CO2 saturation in the main bands is very extreme. There is full absorption within meters or tens of meters. It bounces around and is re-emitted; re-absorbed’ etc until the final emission to space from around the tropopause. The key point here is: because the temperature at the tropopause is constant, increasing altitude of radiation-to-space due to incremental CO2 has minimal effect on the lines of heavy absorption. In fact, in some very strong lines, it looks like radiation-to-space comes from the stratosphere where the temperature INCREASES with increasing altitude. Thus, the impact would be reversed in these lines. I think that you can perhaps discern this effect in some infrared spectra in the middle of the CO2 band, but I’m not sure of this.
The main effect of increasing CO2 comes in lines in the far wings of the main band; in secondary bands and in isotopes, which are emitting to space from below the tropopause (“not saturated”) . You should theoretically be able to say: with CO2 increases in the 1990s, we will see changes in the temperature of radiation-to-space in very specific lines: certain far wings of the main CO2 band in the 700s cm-1; and in specific lines in hot bands.
I was quite intrigued by an article by Santer or someone like that arguing that the height of the tropopause had increased. Think about that for a minute: – if radiation=to-space is occurring at higher altitudes in critical lines (say 200 meters higher), if the lapse rate changed so that the tropopause was higher, this would mitigate forcing from CO2 very strongly.
A pretty good analysis, Steve. Where I take issue is saying something like:
It implies that CO2 after absorbing a quantum of IR then re-emits it. But the collision frequency of gases in the lower parts of the atmosphere is very much larger than the emission frequency for IR by CO2. Therefore almost all of the IR emitted is going to come from black-body radiation and that, AFAIK comes during collisions of molecules. Thus two O2 molecules, which can’t emit IR on their own because of their symmetry, if they interact during a collision can emit IR and do so. So while CO2 will emit some IR in its bands, most of the IR emitted will come from the bulk of the atmosphere and this will to a large degree go directly to space.
When we have added CO2, it will absorb more in the places you mention but the energy absorbed will be thermalized and much of the energy re-emitted into the holes in the IR spectrum and when looked at from space these bands will be augmented over what they would be without the additional CO2. At the same time, as has been pointed out, the CO2 bands will be emitting mostly at colder temperatures and will thus be attenuated. I’m not sure that your point about emission in the warmer parts of the stratisphere affects things much since the amount of gas at those heights are so much lower and thus the energy available to be emitted is small.
Re your last sentence, I agree that the effect is small; I’m just highlighting that the altitude-heightening argument reverses at a certain point.
How do you get “black body radiation” from the atmosphere? I agree that there is bumping of molecules but the radiation can only come from CO2 molecules, water vapor molecules and clouds.
The lapse rate from a pure radiative model would be much steeper than observed. Convection (especially water vapor evaporation and condensation) reduces the lapse rate. So the temperature of CO2 molecules and water vapor molecules at height is not as low as under a pure radiative model.
I’ll try to write up a post on my thoughts within the next month. Otherwise, let me leave it at that as I’m trying to write some other material right now. The topic is interesting but I’ll have to leave my discussion for another day.
Well, I’m going a bit on general principles (and will gladly accept correction based on more than hand-waving). I tried looking a while back on-line to get info on the black-body radiation emitted by the atmosphere and got nowhere. But the point is that anything will emit black-body radiation at frequencies depending on the temperature. The mechanism is easy to figure for solids. For gases it’s more difficult. As I said in the last message, a symmetric gas can’t emit electromagnetic radiation as an individual molecule because there’s no dipole to work with. But when two molecules collide, there will be a dipole set up when they approach each other, and this will occasionally result in radiation being emitted. Indeed there must be radiation emitted in such cases with some probability. It was precisely the problem of why atoms didn’t collapse by the orbiting electrons emitting radiation which was one of the things which led to the formation of the quantum mechanics. In essence they resulted in the charge of the electron being smeared out over the orbit and thus not having a dipole moment. But two molecules approaching, whether or not they are identical (unless both are the same and monoatomic), will set up a rotating dipole which may or may not emit during the time they’re in close proximity. I’m not saying the emission is of real high intensity, but given the small relative concentration of CO2, for instance, it doesn’t have to be.
Dave: are you sure that radiation can occur due to two molecules approaching each other. Where does the energy come from?
Kinetic is the initial source. The molecules themselves of course have an energy state, what it is depending on whether or not they have absorbed energy from other sources.
Any gas molecule has an energy potential, mainly because by definiton it has to be above absolute 0.
Yes, but does quantum mechanics predict a release of energy when two molecules attempt to bump into each other?
You’ll have to ask a quantum mechanic, but it can happen spontaneously, or it can be triggered. I.E. Lasers. energize the atoms, then send a phonton through and you get a cascade.
Same thing here, if they are heated and colide, it is very likely they could let a photon go.
But if you wan’t me to prove it with a Quantum mechanic equation, sorry. But we do know the energy has to be released eventually so the molecule can reach ground state, a collision can initiate that, the molecule being in an unstable state.
re:#32
But releasing the energy via collision is different than releasing it as a photon. As I’m sure you know from elementary physics, a charged body moving through a magnetic field can produce electromagnetic waves. It depends on either the charged body rotating with a dipole moment or the magnetic field changing over time. Most molecules in the atmosphere, in particular Nitrogen, Oxygen and Argon don’t have a dipole moment and thus can’t release electromagnetic radiation by spinning in a field. But if two molecules pass close by each other, their internal electric and magnetic fields will interact with each other and this can result in a circumstance where a photon can be released. It’s a bit tricky quantifying this however, at least for me. You have to have conservation of momentum and the colliding molecules will have other restrictions. You won’t be able to treat things as a two-body problem since at least one of the molecules and usually both with have two atoms in it.
To clarify when I say collision there are mechanical as well as electromagnetic energies.
Compress two atoms at ground state, and attempt to overcome the electrical bands, as well as the strong and weak force of the concerned atoms (in the molecule) and you will release energy. You are converting mechanical force into electromagnetic force.
Think of the piezioelecric effect.
It all gets a bit hairy because your talking about the atomic level which is still not well understood, and even those bits that are get hairy when you start thinking of boundary terms, all atomic talk gets wonky.
Suffice to say if you mechanical collide to molecules, one of which is in a high energy state it is entirely likely that it will release a photon to reach ground. A mechanical force intiated the interaction which can cause an electrical or nuclear reaction.
Axtually the more I think of it.
Take a CO2 molecule and shove it into the muzzle of a particle accelerator, and shoot it at anotehr CO2 molecule.
Do you think you will get particle emmision? I’ll bet money on it.
Granted a realitive low energy colision in the atmosphere has nowhere near that much energy. But if one of those molecules is already on the edge to dump a photon, well there you go.
I think I’d like to write the headline on this one. How about ‘Climate alarmist alarmed at Nature’s editorial policy.’