Climate Audit

Yet another propaganda essay masquerading as a scientific paper has been published (SI here) in the journal, Environmental Research Letters.   The latest entry, Quantifying the Consensus on Anthropogenic Global Warming in the Scientific Literature, written by a team of activist bloggers led by John Cook of the antithetically named Skeptical Science blog,  attempts to further the meme of a 97% consensus of scientific support for a faltering Global Warming movement.

There have been a number of posts, for example,  here, here and here at Lucia’s Blackboard or this one and that at WUWT which discuss the weak data gathering / data interpretation methodology and the truly incredible spin-one’s-head- around algorithm for generating a value of “97” which conveniently ignores a large proportion of the data.  My focus in this post will be to examine some of the other “quantifying” material.

Given the virtual absolute absence  of available data and statistics in this paper, this will not be that easy a task.  The authors have apparently bought into the Climate Science tradition of why should I make the data available if you will only use it to prove me wrong.  I should point out that I have spent much of my academic career doing just that and become reasonably adept at recognizing situations where work might  be shoddy.  This is due to my experiences with consulting on academic research projects, Ph.D. and Master’s theses work as well as outside the university.  When  interviewing the researchers about their project, I would tell them that I would attempt to find everything that was wrong with their planned research.  When it got to the point that this was no longer possible to do, I would be satisfied that the statistical aspects would be adequate for answering the questions that they wished to answer.

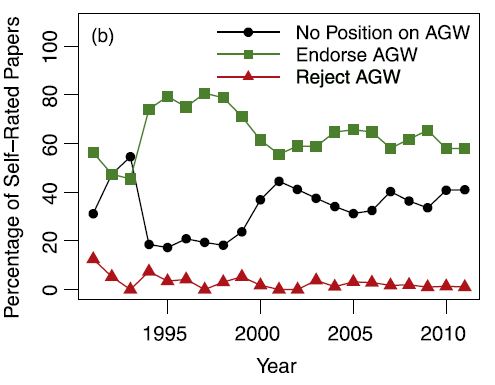
One of the items that caught my eye was Figure 2b:  Percentage of self-rated endorsement, rejection and no position papers.

This figure was discussed in the text of the paper:

Figure 2(a) shows the level of self-rated endorsement in terms of number of abstracts (the corollary to figure 1(a)) and figure 2(b) shows the percentage of abstracts (the corollary to figure 1(b)). The percentage of self-rated rejection papers decreased (simple linear regression trend  -0.25% ±0.18% yr^-1,  95% CI, R² = 0.28; p =0.01, figure 2(b)). The time series of self-rated no position and consensus endorsement papers both show no clear trend over time.

Figure 2(a) showed that the number of abstracts each year was increasing at a very high rate.  This implied that the variance of the percentages calculated for figure2(b) would change substantially from year to year.  Since a “simple linear regression” assumes homoscedasticity (i.e. equal variability) of the data from year to year, this would mean that the early years with very few abstracts would have an inordinately strong influence in the calculation of the parameter estimates as well as possibly distorting the interpretation of the significance of the results.

As well, the model for this regression (which for convenience we will do for a probability rather than a percentage) looks like:  P_k = α + βT_k where P_k is the probability that a paper in year T_k will belong in the category for which the regression is being done (e.g. “rejection papers”).  An observation for that year will look like p_k = n_k / N_k where n_k is the count of papers in years k and N_k is the total number of abstracts in that year.  One should note that p_k is assumed to have a binomial distribution with parameters N_k and P_k.  The full model  becomes  p_k = α + βT_k + ε_k where ε_k is a random variable with mean 0 and variance equal to P_k (1 – P_k ) / N_k .

The data needed to create Figure 2(b) was, you guessed it, unavailable, so I digitized the data in the graph using a simple R programme.  The large symbols used in the graph were not helpful to the process, but I managed to get what appeared to be a very reasonable replica of the various plots.  The replicated plot appears below near the end of the post.

Using creative rounding, I also turned these percentages into yearly counts for the categories each year for later use.  As a check, I calculated both the yearly count totals and the overall category totals.  The yearly counts matched the counts given in Table S2 of the Supplement except for the years 2009 and 2011 where they were each out be 1 in opposite directions.  The overall totals for the categories were

reject          endorse               nopos

40                 1321                    781   :  Estimated from Figure 2b

39                 1342                    761   :  Given in the paper

The differences of size 20 seem to be much too large to be explained as digitization errors (since a check on Photoshop of my reconstruction and the original graph showed an extremely close matchup of points, so this appears to be something that Mr. Cook could address by providing the “correct” values for the totals he gives in the paper.  However it is not the central issue here.

Using the digitized data, the “simple regression was carried out in R.  The comparable statistics to those above for the Reject group were (to all decimal places provided – round as you wish) :

-0.2501658% ± 0.1950723% yr^-1,  95% CI,                 R² = 0.2749;         p = 0.0147   Calculated in R

-0.25% ±0.18% yr^-1,  95% CI,                                         R² = 0.28;                   p =0.01  From the paper

The Cook bound for the confidence interval appears that it might have been calculated from a simple 2 times standard error calculation rather than formally using the appropriate t-value – something one should not do in a professional paper.

As I mentioned earlier, the “simple” regression method assumes equal variability from year to year which is clearly not the case.  In order to correct for this, we need to do a weighted regression where the optimal weights are equal to the inverse of the variance of the data value.  Thus the weights look like:

W_k = 1/( P_k (1 – P_k ) / N_k  ) =  N_k / ( P_k (1 – P_k ))

There is a slight problem here in that the P_k’s are not known.  One could substitute the sample proportions or better still, one can estimate the probabilities from the regression equation,  P_k = α + βT_k.   This is done by alternately calculating the regression and the weights until the process converges (iteratively reweighted least squares).  I wrote a short program for doing this and recalculated the above estimates:

-0.1524997% ± 0.1182535% yr^-1,  95% CI,                 R²  = 0.2772;        p = 0.0142

The magnitude of the slope is reduced by about 39% from the inappropriate unweighted regression.

I repeated this exercise for each of the other groups for which no results whatsoever were calculated because ostensibly  “the time series of self-rated no position and consensus endorsement papers both show no clear trend over time”.  One would think that for interest’s sake, such results would at least appear in the SI.

Endorse Group:

-0.16485% ± 0.7570545% yr^-1,  95% CI,                       R²  = 0.01081;     p = 0.654              Simple Regression

-0.4350717% ± 0.5419943% yr^-1,  95% CI,                 R²  = 0.1294;        p = 0.1093            Weighted Regression

No Position Group:

0.4149549% ± 0.7862663% yr^-1,  95% CI,                  R²  = 0.06034;     p = 0.283              Simple Regression

0.603483% ± 0.570961% yr^-1,  95% CI,                       R²  = 0.2048;        p = 0.0394            Weighted Regression

Using a more appropriate regression can produce substantial changes in the results.

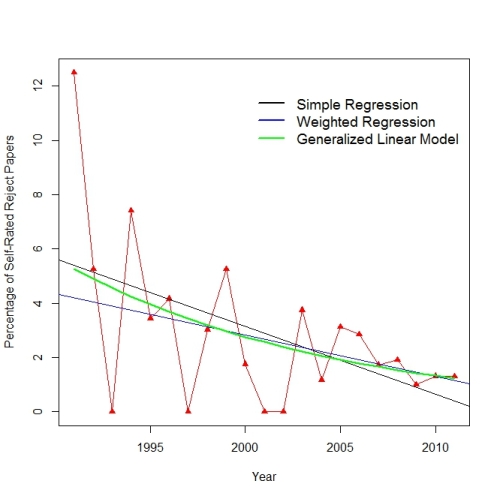
So is this the end of the story?  Not quite.  Unbeknownst to some amateur statisticians, using regression to analyze this type of data is not recommended.  For example, if one were to use the Cook paper regression to “predict” the probability for the Reject group for any year from 2013 on, they would get a negative value ( possibly because retractions would exceed new publications???).   Methodology  termed Generalized Linear Models has been developed for exactly this type of situation.  In our case, we will use a slightly different model:

P_k = exp(α + βT_k) / (1 + exp(α + βT_k))

where exp(x) represents the exponential function e^x.  This particular model is also known as logistic regression.  Fitting is done using maximum likelihood techniques and interpretation of the estimated coefficients differs somewhat from the regression case.  Unlike linear regression the result is always between 0 and 1 with no negative probabilities.  Also, confidence intervals for probabilities are usually not symmetric about the estimated value.

Using the glm() function in R, the calculations were done   for all three groups:

Reject:

…………………………Estimate              Std. Error             z value             Pr(>|z|)

(Intercept)          144.97037            54.51333              2.659          0.00783

year                   -0.07427              0.02720                -2.731       0.00632

Mean annual rate of change from 1991 to 2011: -0.2007284

Endorse:

………………………..Estimate              Std. Error             z value          Pr(>|z|)

(Intercept)          38.788789            18.676384            2.077       0.0378

year                  -0.019095            0.009308              -2.051    0.0402

Mean annual rate of change from 1991 to 2011: -0.4384528

No Position:

…………………………Estimate              Std. Error             z value    Pr(>|z|)

(Intercept)          -55.417983          19.119586            -2.898    0.00375

year                   0.027343              0.009528              2.870     0.00411

Mean annual rate of change from 1991 to 2011: 0.60276

You will note that all three of the groups now seem to have statistically significant rates of change with the Endorse group showing a decrease of almost 9 percentage points over the 20 year period.

The plot below shows the distribution of the Reject group with associated regression lines and the fitted GLM.

All of the groups with associated GLM fits:

All of the R calculations and the data used are available by running the following lines in R (you may need to fix the quotes first):

dfile = “http://statpad.files.wordpress.com/2013/05/cookpost.doc ”
download.file(dfile, “cookpost.R”, method = “auto”, quiet = FALSE, mode = “w”,cacheOK = TRUE)

Open the script cookpost.R .