Last year, when Moberg was published, I pointed out witha slightly arched eyebrow that one of the two most important contributors to any 20th century HS-ness in Moberg was the increasing percentage of subpolar foraminifera (G. Bulloides) in the Arabian Sea – intuitively not a direct indicator of warming. Having visited the foraminifera literature in more detail in my reading of Hansen (who is more interested in G. ruber), I noticed some pertinent discussion of G. Bulloides in the Arabian Sea, which confirmed my initial reading. G bulloides percentage directly indicates upwelling cold water, which in turn is linked to a stronger winds (i.e. stronger monsoon), which is said to be associated with warming onshore.
Moberg stated that proxies were chosen according to the following policy:
Records that have been interpreted as reflecting annual mean temperatures were preferred, but a strict application of such a criterion would have led to a too limited amount of data. Therefore, data representing seasonal (mainly summer) temperatures were also allowed.
Here is Moberg’s diagram of the percentage G. Bulloides is shown in Figure 1, with his description in the caption (my bold),

Figure 1. Percentage of G Bulloides in an Arabian Sea core. Original description: A combination of two marine sediment records from the Arabian Sea [Gupta et al 2003; Overpeck et al 1996] in which the percentage of the foraminifera Globigerina bulloides reflects the extent of ocean up-welling, which is determined by the strength of monsoons, which in turn indirectly reflect both summer and winter large-scale temperature changes through the differential seasonal heating and cooling of the Asian continent and surrounding oceans [Overpeck et al 1996]. We used data from Core 723A [Gupta et al 2003;] for the early years up to 1390 A.D. and data from Core RC2730 [Anderson et al 2002] from 1391 to 1986 A.D. (c.f. Fig. 3c in ref. 15). Although this record reflects temperatures only indirectly, it was included to improve the balance in the geographical distribution of proxy sites.
Conan and Brummer 1999 have an interesting discussion of foraminera in a nearby location – offshore Somalia at about 11N; 52E in an upwelling zone. They studied both foraminifera both in a trap at 1265m and coretop at 1625m. Figure 2 below shows the annual cycle of sea surface temperature at the sites – with a remarkable drop in SST during the summer upwelling.

Fig. 2. Sea surface temperature at the mooring site (upper panel (a)) for 1992}1993 and fluxes of particles ‘100 lm to the sediment trap at 1265 m water depth, 268 m above the bottom (lower panel (b)). The large circles are in situ measured, small circles are derived from remote sensing and squares are monthly averages (see Brummer et al., 2000). Please note that particle fluxes are displaced by 2 weeks to account for the delay in shell production and settling of the planktic foraminifera. Note the different scale at right for the `unidenti”ed fragmentsa category which predominantly consists of bioclastic grains.
The next figure shows the seasonal distribution of foraminifera. You will notice that G bulloides is associated with cold upwelling water.

Conan and Brummer Fig. 5. Species composition (%) of planktic foraminifera’100 lm (a) and’125 lm (b) of sediment trap MST8-B.
Finally the last figure shows the seasonal distribution of shell production – as annual yields are obviously integral/

Conan and Brummer Fig. 3. Seasonal shell fluxes of planktic foraminifera (shells’100, ‘125, ‘150 lm m~2 d~1) intercepted by sediment trap MST8-B at 1265 depth, 268 m above the sea #oor in the Somalia Basin from June 7,1992 to February 14, 1993. The peak flux observed in the 2 samples of October in the’100 lm fraction is probably caused by resuspension of bottom sediment material from the shelf and upper slope but did not affect the’125 lm fractions.
I’ve also mentioned before that the values of this proxy are nowhere near being normal – they are more like a uniform distribution. Despite the assertions that the proxies were selected to “reflect” temperature, the reflection here is through a very distorted mirror. Additionally, although the proxy increases are interpreted to show increased warmth, they do not reflect warmth in the area of the proxies but hypothesized warmth elsewhere as a result of increased winds. To the extent that Yang’s China composite draws on this onshore area, isn’t this already counted?
References:
S.M.-H. Conan, G.-J.A. Brummer 1999. Fluxes of planktic foraminifera in response to monsoonal upwelling on the Somalia Basin margin Deep-Sea Research II 47 (2000) 2207}2227
Gupta, A. K., Anderson, D. M. & Overpeck, J. T. Abrupt changes in the Asian southwest monsoon during the Holocene and their links to the North Atlantic Ocean. Nature 421, 354-357 (2003).
Overpeck, J., Anderson, D., Trumbore, S. & Prell, W. The southwest Indian Monsoon over the last 18 000 years. Clim. Dyn. 12, 213-225 (1996).
Anderson, D. M., Overpeck, J. T. & Gupta, A. K. Increase in the Asian SW Monsoon During the Past Four Centuries. Science 297, 596-599 (2002).




13 Comments
(nit) Need the ref for Yang also.
(substance) What does China have to do with this area of the ocean?
Steve
This sounds rather like nit picking. Does it matter if a proxy indicates temperature where it is located or 1000 miles away, as long as it it reliable? You have done some great work exposing the flaws in proxy studies, but sometimes I feel you do rush in exclaiming, its wrong, its wrong!! whenever a new proxy study comes out indicating warming, often at you own admission before properly understanding the background. Yes sometimes you are right and things look dubious, but not always and sometimes it just looks a bit foolish.
The hypothesised link between bulloides, upwelling, monsoonal circulation and temperature was clear in the original paper (at least as clear as it is possible to be in a nature format paper). I really don’t think you have uncovered anything new here.
That statement doesn’t bother any of you – even a little?
If I remember correctly Moberg tested for removing any single proxy to see how much it changed the final result, and it didn’t to any significant degree.
#5. Relative medieval-modern levels in Moberg are not as robust as you might think.
Given that perecntage G bulloides has a negative relationship with SST – which is what it is directly measuring – so if the proxy were calibrated to SST, wouldn’t the proxy have a negative effect?
I disagree that Moberg clearly stated that increasing percentages of G bulloides were evidence of colder local SST – or that he clearly articulated why colder SST offshore Oman whould be regarded as especially strong evidence of global warming.
Re #5, Thomas, thanks for your comment. You say:
However, with 11 proxies this is not at all surprising. Suppose we have 11 proxies. All but one of them are randomly distributed around 100, with a standard deviation of say 10, and the final proxy is distributed around 200, with a standard distribution of 20. Let’s say we’re looking at the mean and standard deviation of the average of the proxies as our variables of interest.
The mean of all of the proxies is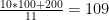 . The standard deviation of this mean adds in quadrature, so it is
. The standard deviation of this mean adds in quadrature, so it is  .
.
If we pull out a correct proxy, the mean of the proxies is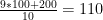 . The standard deviation of the results adds in quadrature, so it is
. The standard deviation of the results adds in quadrature, so it is 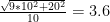 .
.
If we pull out the incorrect proxy, the mean of the proxies is . The standard deviation of the results again adds in quadrature, so it is
. The standard deviation of the results again adds in quadrature, so it is  .
.
Now, this is an extreme example, where one of the proxies is badly wrong, and still pulling out any one proxy doesn’t make much difference (less than 10%).
And in the real world, things are mushier, and errors are never in quadrature, so the removal of an incorrect proxy may, paradoxically, make your results closer to reality … so in fact, finding things basically unchanged after removing any single one of eleven proxies doesn’t mean much.
w.
Re #8, a postscript … all of this assumes that you are not mining for hockeysticks, in which case all bets are off. However, from what I understand of Moberg, he’s not doing that …
However, what he is doing is mining for non-normal datasets. If a distribution is fat-tailed, then normalizing (subtract the mean, divide by the standard deviation) emphasizes the tails. This may be correctable if the series is autocorrelated, because the lower effective “N” increases the standard deviation … but on the other hand, it may not be. I doubt if Moberg made any such correction, at least I find no mention of it.
I suspect that in fact, this is a fundamental flaw of his method. Essentially, he is doing a Fourier analysis of sorts on the data, breaking it down into sinusoidal or quasi-sinusoidal frequencies. The problem is that a sine wave is non-normal, since the value spends more time at the extreme values. Let me go take a look …
… 1 hour pause for confirmation …
Yes, that’s the case. I constructed a synthetic series by averaging two different sinusoidal proxies. I had constructed the proxies previously through the addition of 4 sine waves that differed in frequency, phase and amplitude, so I knew the actual underlying functions. These two proxies had the same four underlying frequencies for both proxies, and differed only in phase and amplitude. Here are the proxies and the data.
The first proxy (blue) explains 23% of the variance, and the other explains 58%. Of course, between them they explain 100% of the variance.
Then, a la Moberg, I did the following:
1. Normalized the proxies.
2. Extracted the underlying four sine waves.
3. Averaged the corresponding frequencies.
4. Recombined the averaged sine waves.
5. Adjusted the mean and standard deviation of the reconstruction to that of the data.
Here are the results …
The problem, of course, lies in the incorrect calculation of the standard deviations of autocorrelated time series. While this data is extremely autocorrelated, the difficulty is clear. Without adjustment for autocorrelation, Moberg’s method contains an unknown error.
w.
re 9: After one semester of circuits an engineering student would say that your filter is ringing. If you were measuring hydraulic pressure, I’d say there was an air bubble in somewhere in your tubing. And if the red line represents the right rear wheel on your 1959 VW Beetle, you need new shocks.
Re #5
Thats because Moberg inventively included two dodgy proxies for temperature.
Learning from Mann et als “mistake” of only including one dodgy proxy (Bristlecone), Moberg, so he could say his results were “robust” WRT removal of any single proxy, included two.
If you look through StevM’s archive page More on Moberg you will find graphics for each of Mobergs proxies, and they include two suspect ones, #1 and #11that both “coincidentally” have a Hockey Stick shape to them.
Leave only one in and Mobergs process still overweights it and produces a “robust” Hockey Stick.
link
How clever of them. Not.
Here is a figure from a Gulf of Mexico core reported in Poore et al 2003, which, on a long scale, shows increasing percentage of G bulloides as we approach the last Ice Age. As a thermometer, percentage G bulloides shows cold water not warm water.
Figure 3. Stratigraphic plots of relative abundance of selected planktic foraminifers, d18O for Globigerinoides ruber (white variety) and winter sea-surface temperature estimates in RC 12-10. Data are from the work of Dowsett et al. [2003b].Poore, R. Z., H. J. Dowsett, S. Verardo, and T. M. Quinn, Millennial- to century-scale variability in Gulf of Mexico Holocene climate records, Paleoceanography, 18(2), 1048, doi:10.1029/2002PA000868, 2003.
One Trackback
[…] on Arabian Sea G. Bulloides On an earlier occasion, I observed that one of the key Moberg series (and now an essential Juckes series) was the Arabian Sea […]