There are a few other blogs that from time to time do detailed analyses of what people are doing, not dissimilar in format to what I do. Last year, in Apr 2006 shortly after publication, I observed here that the upper and lower confidence intervals of Hegerl et al crossed over.
In Feb 2007, Tapio Schneider published a Comment in Nature observing that the confidence intervals in Hegerl et al were wrong. Hegerl published a Reply and replaced the Supplementary Information with new data (I kept the old version in case anyone wants a comparison.) James Annan recently discussed the matter , linking to my graph, acknowledging it in a business-like way. About the new Supplementary Information, he said:
There is now a file giving the reconstruction back to 1500 with new confidence intervals, which no longer vanish or swap over. This new data doesn’t match the description of their method, or the results they plotted in their Fig 1 (which is almost surely a smoothed version of the original supplementary data).
He went on to say:
Hegerl et al used a regression to estimate past temperatures anomalies as a function of proxy data, and estimated the uncertainty in reconstructed temperature as being entirely due to the uncertainty in the regression coefficient. The problem with this manifests itself most clearly when the tree ring anomaly is zero, as in this event the uncertainty in the reconstructed temperature is also zero!
Maybe UC (or Jean S who we haven’t heard from for a while) can comment on this. This comment still doesn’t seem right to me as I can’t think of why the uncertainty would be zero merely because all of the uncertainty was allocated to the regression coefficient. I still can’t get a foothold on what they’re doing here; Annan said that Tapio Schneider had been unsuccessful in getting Hegerl to document what they did in any of the calculations. I’ll write but I’m not optimistic about my chances. I’m up to about 20 emails with Crowley trying to find out how they got their Mongolia and Urals series, without any success.
Eli Rabett observed that Huang et al appeared to have done the same thing in a borehole study. In the caption, Huang refer to Bayesian methods being used, so maybe there’s a clue for someone. Whatever these folks are doing, it’s not a totally isolated incident. Who knows – one day,we might even find out how the MBH99 confidence intervals were calculated – presently one of the 21st Century Hilbert Problems in climate science.
References:
Hegerl JClim 2006 here
Hegerl Nature 2006 here
Hegerl SI here
Climate Audit 
25 Comments
if y = a + bx + e, and you want to know the variance of the estimated value, y^, that variance is not zero when you are comparing the actual time series with the fitted values and one of the fitted values is equal to the actual value. If that is what he is saying here, he’s nuts.
You just have to look at the ANOVA. http://en.wikipedia.org/wiki/ANOVA
Confidence intervals, regardless of method, cannot vanish or cross over. If one does end up with such confidence intervals, it is a sure sign that something is seriously wrong in the way calculations have been done. If it happened to me, I would withdraw to an isolated room, not get out until I figured out my error and I would be ashamed to tell anyone about whatever stupid mistake I made.
However, this paper got published. Sad.
Here is what I mean: The width of the confidence interval for mean response in a simple OLS regression with one independent variable depends on the standard error of the mean response (which, in turn, depends on the x-value at which mean response is being evaluated). We have, from the Intro Stats textbook I use in the undergrad stats class I teach,
If
, this reduces to 
which cannot be zero (unless the regression line is a perfect fit) because s is the square root of MSE.
Now, confidence intervals for mean response will be narrower than prediction confidence intervals (for the same confidence) but they cannot vanish and the lower and upper bounds cannot cross.
I am baffled.
Sinan
It looks like the uncertainty is all assigned to the regression co-effecient of the anomoly (i.e. to b in y = bx + e); consequently, the upper and lower bounds flip over when the anomoly passes zero.
Correction to #2:
In the formula for the standard error of mean response, there is a sum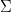
sign missing from the denominator of the second term in the square root.
Also, I mention the undergrad intro stats textbook to underline the fact that this is basic, elementary stuff. Vanishing confidence intervals or crossing upper and lower bounds is an indication that the author of the article ought not be trusted to balance his own checkbook.
Sinan
I sent the following inquiry to Gabi Hegerl:
#5. Gabi Hegerl replied as follows:
Did you plot that diagram yourself? If so, is the R code easily available somewhere?
I’m asking because they look an awful lot like they are merely scaled versions of each other. It would be interesting to check if that’s true.
I’ll try to post up the code today. It might be an interesting project for statistically-interested people to decode their uncertainty methodology. I’ll post up as much relevant data as I have.
It looks to me as if they originally used a statistical recipe in the wrong context.
Trying to imagine a proper context: suppose you tried to regress national GDP against national population using data for 100 countries.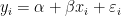
would be a bad model since it is obvious that a country with a tiny population would have a tiny GDP. 
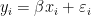would be almost as bad as the absolute values of errors would clearly be related to population. 
starts to make more sense.
But that model only makes sense if all the values are positive and if errors tend to increase with the independent variable. That doesn’t apply here, so it was the wrong method to apply. It probably stemmed from a desire to have everything at zero in the base period for calculating anomalies. And the graph should have been spotted by the peer reviewers.
I have heard it said before, that a lot of these results that involve statistical techniques lack the input of suitably qualified statisticians. Am I right in thinking that elementary statistical errors are being made due to lack of competence? If this is the case, then the quality of a lot of this kind of research must be suspect.
Very briefly:
something odd in the manuscript figure 2 as well, cross overs..
BTW,
‘negative bias of the variance of the reconstruction’ in supplementary refers to vS04. I believe that this negative bias is a result of ‘natural calibration’ assumption, i.e. optimal solution in the case where P and T are obtained from joint normal distribution. I’ll return to this topic later ( and if I’m wrong I just disappear 😉 )
Recommended reading:
Confidence and Conflict in Multivariate Calibration (PJ Brown, R Sundberg, Journal of the Royal Statistical Society, Ser B, Vol 49, No 1, 1987)
Multivariate Calibration – Direct and Indirect Regression Methodology (R Sundberg)
Those papers contain some ideas how to deal with uncertainties in this context (filtering theory is another way, but it doesn’t seem to interest climate people ).
Here is how one can get “confidence” intervals of zero width in temperature reconstructions:
1) Estimate a regression model
T – [T] = b(p – [p] + eta) + eps (*)
where T-[T] are temperature anomalies (mean temperature [T]), p-[p] are proxy anomalies, and eta and eps are error terms.
2) “Reconstruct” temperature anomalies by taking expected values in the regression model (*) and plugging in estimated regression coefficients b’ (and estimated mean values [T] and [p]).
-> The “reconstructed” temperature anomalies T-[T] are zero for any value b’ of the estimated regression coefficient if the proxy anomaly p-[p] is zero.
3) Vary the estimated regression coefficient b’ within estimated confidence limits and “reconstruct” temperature anomalies as in (2) for each value of b’.
-> The “reconstructed” temperature anomalies will still be zero for all values of b’ whenever p-[p] is zero.
4) If one infers confidence intervals from the reconstructed temperature anomalies for the different b’ for each year, they will have zero width whenever p-[p] is zero. Of course, it makes no sense to estimate confidence intervals in this way.
This seems to be what Hegerl et al. were doing and what led to their manifestly wrong confidence intervals for the reconstructed temperatures.
Schneider’s point in the Nature comment, however, seems to be more general. Hegerl et al. base their inference about climate sensitivity on the residual difference between the “reconstructed” temperature anomalies and temperature anomalies simulated with an EBM. Schneider points out that
While the error terms eta and eps do not enter the expected value of the difference between EBM temperature anomalies and reconstructed temperature anomalies, they do enter the variance of the residual difference. The variance of the estimated regression coefficients contributes to the residual variance, but so do the variances of eta and eps. This is elementary regression analysis: The variances of eta and eps are generally greater (by a factor of order sample size) than the variance of b’.
#12
Clarifying posts are appreciated, thks (and posters should not be worried about making mistakes, if you make an explicit mistake, gavin drops by and corrects it, so no worries ). It is 1959 in climate science in statistics sense, Williams just published Regression Analysis. Next year will be interesting, as Kalman will publish his A New Approach to Linear Filtering and Prediction Problems.
#12. That makes total sense as an explanation. That’s unbelievable. What a joke. I’ll make a separate post on it in a few days.
Any updates on this?
It’s hard to imagine an error of this magnitude being made by an author and then not being caught by co-authors, internal reviewers, peer reviewers, co-editors, editor. The crossing over of the curves is an obvious sign something’s gone wrong. An undergraduate could tell you that.
Steve M, look at the original confidence interval in the Nature 2006 paper, the region in gray. Why is the confidence interval so thick in those problem areas where the upper and lower bounds cross over? The answer, which you get in the form of a delay in graphics redrawing when you zoom in close, is that the authors have heavily thickened the lines of the gray graphic object. (If they were thin, the pinch would be obvious.) Now why would they do that? To hide the fact that the confidence region pinches as the bounds cross over?
Anyways, this is probably why reviewers never caught the error. But it would be nice to know to what degree this deception was intentional.
“Hide the crossover”.
The new SI at least answers john lichtenstein’s #5 from the previous thread:
The new SI (which starts from 1505) shows the CI’s around 1650 and 1750 to be very wide.
Still, as Annan argues, the CI’s are wrong. In order to get the uncertainty on the inferred value, the uncertainty in the observed value (the proxy value on which the temp reconstruction is based) has to propagate through the uncertainty in the regression coefficients. It makes no sense to assume all the uncertainty comes from the standard errors in the estimated regression coefficients. Some of it must come from sampling error from the estimation of the means.
It is very important to know exactly what these folks are doing.
Some notes / questions:
TLS uses first principal component, minimizes perpendicular distances from data points to the line ( a new line to my calibration-line-plot ) ?
In Hegerl J. Climate paper
I think this is an misunderstanding. IMO Coehlo explains CCE and ICE quite well, and Hegerl et al didn’t read carefully. ICE requires prior distribution for temperatures, and another viewpoint of ICE was just developed in http://www.climateaudit.org/?p=1515#comment-108922 and following comments. If I were a reviewer, I’d stop reading that manuscript right there, page 7. ( I don’t have the final version, was anything corrected? ). I’m not surprised that their CIs went wrong..
Suppose:
inferred Temperature = A * Proxy measure + B
where A, B are regression parameters, each with standard errors, and Proxy P is subject to sampling error.
Then the error in the inference T is the quadrature sum of the errors in A*P and B, and the error in A*P here is the straight
sum of the relative errors in A and P.
Is that not the correct way to compute the confidence level for a quantity inferred from an error-prone calibration? That’s what I learned in high school physics, anyways.
Gabi Hegerl has sent me the following email last week in response to my request for further particulars on her method:
Just so that I meet the requirements of other readers, UC and bender, can you summarize any questions? BTW I got a copy of the Hegerl J CLim article as published posted up here Ther references ot an SI have been removed and there is no SI at the J Climate website.
Re #20
Steve M,
The URL for the Hegerl paper is a bit off. It looks to be http://data.climateaudit.org/pdf/Hegerll07.jclim.pdf
James Annan writes:
Man, that’s just plain and fancy footwork. I can’t offhand think of any physical measurement that has a confidence interval of zero. Examples, anyone?
w.
Re #23 That remark baffled me, too. (I didn’t say anything because I’ve been commenting too much lately.)