Many climate studies use an equirectangular projection, in which lines of latitude and longitude are equally spaced, to graphically summarize data. An example is the following figure from Hansen et al 1988, discussed here recently under the topic Hansen and Hot Summers:

John Goetz uses the same projection in his recent thread here, Historical Station Distribution
While this projection is handy for plotting locations, it unfortunately distorts areas by a factor of the secant of longitude. The result is that areas near the poles are greatly enlarged, albeit not by as big a factor as in the Mercator projection. The result is that a temperature anomaly near one of the poles, as in the lower panel of Hansen’s graph, will appear to be disproportionately important for average global temperature. Likewise in Goetz’s graphs, stations will appear to be far more sparse than they really are as we move away from the tropics.
In order to prevent this area distortion while retaining a rectangular map, the vertical axis must be compressed by a factor of the cosine of latitude in order to offset the secant effect. This is done in the 1772 Lambert Cylindrical Equal Area projection. The following image is linked from Carlos Furuti’s webpage on map projections:

Unfortunately, the Lambert projection greatly distorts shapes near the poles, and makes features difficult to locate. A much better option for presenting climate data without area distortion is the 1805 Mollweide projection

I posted these graphs earlier as comments (#62, 73) on the Historical Station Distribution thread, but as they were somewhat offtopic there and of interest in their own right, I am reposting them here.
In a comment on that thread (#66), Steve McIntyre has already remarked,
#62. Equi-area projections are used in many contexts. In terms of graphic presentations, you’re 100% right and anything other than equi-areal should be banned from scientific journals.
In practical terms at my level, the only issue is the availability of routines in R (and for someone else Matlab). Doug Nychka of NCAR maintains the R-package fields. He’s very responsive to inquiries. I’ll check the manual and otherwise check with him.
and (#71),
http://cran.r-project.org/doc/packages/mapproj.pdf has a package with equi-area maps.
Somebody should be able to locate parameters that yield a “good” map for representing areas in climate contexts.
Mr. Pete, #76, remarked, “If you modify latitude by sin(lat in radians) you get the simplest equal-area projection. No need to use fancier things for basic display.”
This is what is known as the Sinusoidal projection

I like the Mollweide much better, as it gives far less shape distortion, and uses the available space better: Both are the width of the equator and the height of the prime meridian.
However, Mollweide uses fraction = .79 of this box, while the Sinusoidal only uses
= .64 of this box. Thus, Mollweide gives about 23% more informational area within the same size figure.
The formula for Mollweide is a little complicated, and involves solving a transcendental equation numerically (see above Wikipedia article for formula or Furuti’s site for derivation). However, if Mollweide could solve this with an 1805-vintage analog computer (pencil, paper, compass, straightedge and French curve), a modern digital computer should have no problem with it either.




147 Comments
Hu,
If you can provide the Vbasic routine so I can use it in Excel, I’d happily update my plots.
(Yes, I said Vbasic and Excel. No laughing please)
Hu, I love your stuff…but your html skills are, umm, well, not as good as your stat skills. Don’t forget to close you tags.
ACTUALLY…all I need is a new table with the latitude and longitude of each station replaced with the x and y values needed to perform the projection. Can you simply update the GHCN v2.temperature.inv file with the appropriate values for the Mollweide projection and post the file here?
If my calculations are correct, the degrees at the poles are 111 x 2 then 1/3 way to the equator 111 x 55 then 2/3 are 111 x 96 then there 111 x 111
I’m rounding, it’s actually 110.94 x 1.95 per degree for the first degree at the pol and gets larger the farther down you go each degree, but I’m not doing all 90 of them. There’s a calculator someplace on a geo site that does tho, I forget where.
So that would put 2×2 at
29 sqkm (about 865 km of area or the square root of ~222×4)
157 sqkm
207 sqkm
222 sqkm
And 5×5 at 74 392 517 556
The shapes move from triangles to squares on the way to the center. So the farthest away a two stations in a grid can be for the 5×5 is the diagonal of a 550ish x 550ish square at the equator (308,000 km of land).
I probably messed up all the calculations tho. 🙂
Re #2,
This type of code works OK here in the comment windows, so I’m not sure yet what went wrong. I think if I just pasted the whole thing into the comment window, it would come out fine, but perhaps there is some way to fix the post. Have e-mailed SM for advice.
Re #1 and 3, I’m not saying I know how to generate maps of any sort, but wish I could. Actually, Craig Loehle’s associate Mike Martin generated a nice Mollweide graph of proxy sites that was published with our corrected reconstruction article. I’ve asked Craig for tips on software.
I could easily write a GAUSS program (similar to MATLAB) to translate longitude and latitude into Mollweide x-y coordinates. The problem is getting the continents to appear nicely.
These are the Angell radiosonde stations in mollweide:
You could also use GMT (GNU open source package from Soest university Hawaii)
http://gmt.soest.hawaii.edu/
#5 Hu
Trust me, if someone can run the lat/lon coordinates found in the the GHCN v2.temperature.inv file through a program to create the equivalent x, y coordinates for a Mollweide projection, I can create an Excel graph with the proper image as a background. That is all I did on the scatter plots I displayed earlier.
The Mollweide and Sinusoidal projections are normally scaled so that the equator is twice the length of the prime meridian. Let’s see if these work:
It seems that the post editor, unlike the comment editor or the last millenium HTML the I’m used to, wants a / before the > on a tag end.
Notice how the Mollweide (top) fills the equivalent box much more fully than the Sinusoidal, and therefore has a larger overall scale. At the same time it has far less shape distortion — the Sinusoidal N. Am looks like it just swallowed a whole bottle full of hair gel, while its Greenland is anorexic.
The R-packages mapproj has functions that plot these projections. I experimented a little. The Mollweide projection is in the package as were the sinusioidal and cylindrical equal area projection and many other interesting projections. In the plot of meridians here, the meridians are transformed into place with the function mapproject, so it looks like the R plot functions can be used without a lot of difficulty so that things that can be drawn in a rectangular space can be coerced onto this shape.
##MOLLWEIDE
map(“world”,proj=”mollweide”,fill=TRUE,col=”grey80″);
lines(mapproject(list(y= -89:89,x=rep(-174.9,179) )),col=4 )
lines(mapproject(list(y= -89:89,x=rep(-174.8,179) )),col=4 )
a=seq(-60,60,30); for(i in 1:5) lines(mapproject(list(y= rep(a[i],3),
x= c(-175,0,-174))),col=4,lty=2 )
a=seq(-150,150,30);
for(i in 1:length(a)) lines(mapproject(list(x=rep(a[i],181),y= c(-90:90) )),col=4,lty=2 )
There’s something funnny in the display at 60N and I’ve asked the author about this; also there’s more white than I like in the image border. The EW divide is at 174.8W or so.
Here’s another projection from IPCC AR4.
This appears to be an Eckert IV projection (one that was not in the R pacvkage).
Of all the stupid things which you guys complain about in Climate Science, this has to be the dumbest and most inconsequential. Of course most of the things you “auditors” complain about are stupid and inconsequential. This is just the dumbest.
This is from a post I made in the Climate Audit forum a while back:
I have a pet peeve with charts like this one from the GISS (from the NY Times, 1997 warming vs. 1950-78 average):
I have many issues with this chart, not the least of which was the fact that it fills in data for large swaths of the earth for which we have no data. However, my pet peeve is that the GISS is essentially fibbing here by using a straight cylindrical projection of the Earth. We all know from junior high school that there are a lot of ways to project the globe onto a flat sheet of paper, all of which are imperfect. However, for a chart like this, one really needs an equal area projection. In an equal area projection, a square inch at the equator represents the same surface area as a square inch at the poles. The GISS is NOT using an equal area projection (neither is UAH). In fact, in the projection they are using, the area at the poles is wildly exaggerated. Since the north pole is the area of the earth with the most anomolous measured warming, the chart visually overstates the amount of global warming. That whole top red band is really probably about the size of a few pixels in Africa.
It turns out, though, that there are some good free tools available to do just this kind of task. With these tools I was able to convert the chart above to an equal-area projection (using the Eckert IV method):
One can see that the visual message is certainly different when projected correctly. This tool was so simple it took me less than 10 seconds to make this reprojection, and it had options for many, many different types of projections. The source of this fabulous tool that the GISS should have used is … the GISS! Its free and a lot of fun.
I can’t tell if I am linking the images above correctly. If they do not come through, you can see my post here.
I wonder if NASA knows about these types of projections 🙂
For Rattus:
I would agree that map projection is the least of the problems one can identify in the GISS map. However, I think the examples I have shown better illustrate why the chartmanship can be important. Besides, if one can do it right with 10 seconds extra work, why not do it right?
Jae-
I fell over laughing a couple of weeks ago when I found that the best tool to correct the GISS chart to an equal area projection was available free from … the GISS. LOL. It is a fun too, try it.
I edited the article so that a) the images appeared and b) the images weren’t so big that it nearly crashed my browser.
Does this do it for everyone:
Re Steve # 10:
The 1906 Eckert IV is described briefly at http://members.shaw.ca/quadibloc/maps/mps0405.htm. It sounds like a valid compromise between the Mollweide and the Lambert projections. Its outline is evidently two semicircles on either side of a square. As such, it occupies even more of the 2X4 box than Mollweide, and hence shows even more detail. It’s a little misleading, however, that the N. and S. Poles have been dilated from single points to half the width of the map.
The IPCC Figure 3.19 you show looks like an Eckert IV that has been fudged slightly so as to make it a little taller, by adding the gray bands. If these were just blank gray it wouldn’t matter (aside from being confusing). However, Greenland has somehow been extended up into the gray band, instead of cutting off just short of the top of the actual map!
Re Coyote #12 —
Bravo! That’s exactly my point.
John A (#16) writes, “I edited the article so that a) the images appeared and b) the images weren’t so big that it nearly crashed my browser.”
Thanks! However, as I note in #8, both the Mollweide and Sinusoidal should have a 2:1 aspect ratio, eg 600 X 300. I tried to set them this way in my original effort that had the bad(?) tag ends, but somehow my heights and widths got lost in translation. You have both at 640 X 400 presently in the main post, which is a little too tall.
Re Hans #6, I’m now inclining back towards Mollweide and away from Eckert IV for this kind of image, since it indicates that the Arctic stations are fairly close to one another, whereas Eckert IV would make them appear more widely separated than they really are.
Coyote #12 —
Will the GISS tool let you do the same graph in Mollweide? I’d like to see how it looks.
Here’s another projection that’s similar to Mollweide, but which is maybe even a little better at the poles
Re #10,
Two more of these AR4 “Extended Eckert IV” maps were discussed recently in the Hansen and Hot Summers thread:
Although the extra bands at the top and bottom are blank gray, they still give the impression that the polar regions are more important than they really are.
My bad:
On closer examination, these AR4 maps are not Eckert IV, even if the spurious top and bottom bands are removed. In a true Eckert IV, the outer quarters are semicircles that meet the central square on a tangent. The outer lobes of these maps meet a central rectangle with a cusp (with or without the mystery band).
So maybe they’re not even equi-areal. Greenland does look a little too large, even if it is not extended into the band.
Re #22,
Beautiful, beautiful!
So now explain to us why the Turks, Japanese and Americans are such temperature fetishists!
#22 For me it is not only a much more self-explanatory illustration, but the stations along the Greenland coast show up nicely.
Hu, I wasn’t speaking of sinusoidal. I may have had my trig upside down, but a simple cos() or sin() function (depending on how you use it) generates the Cylindrical Eq-Area projection as you showed. [Unless I’ve really lost my marbles, cos(phi)+sin(phi) = 1, so it’s all a question of how you use the function!]
We tended to use this for most ‘raw’ GIS display purposes because it is so much faster than any other projection method. Once a presentation display or layout is needed then of course one goes to whatever projection the user desires. The correct (bit-invertable) math on such things can be quite hairy.
One final comment: the Robinson projection was chosen by Nat’l Geographic and many others as their std projection because it gave the most pleasing compromise: almost (but not quite) equal area, and it looked “normal” to most people.
But here, we’re talking science not promotion, and the need for the spatial accuracy of equal area is more significant.
Repost of p=2015 from Sept 1st last year under “Hansen’s Bias method”.
A few quick thoughts on the range of influence of pairs of observations near the Poles. Just for fun.
Let’s assume that points up to 1000 km apart can be used to help predict each other re temperature, as Hansen accepts and uses in his adjustments.
I do not know when Hansen uses a straight line, a stepped line, a logarithmic line or a line to a power or inverse power to weight for distance when comparing and weighting sites, as opposed to adjusting for temperature change over time. I’m confused.
Mental exercise. Start with a point at 500 km North of the South Pole, say Mt Glossopteris at longitude 120 degrees West. (Glossopteris was a plant found in fossils, as geologists know). Call this our Reference Point, RP.
A point 1000 km south of the RP is on the other side of the world, 500 km from the Pole. That is, at noon at the RP it is midnight at this point. (We assume here that the South Pole is fixed at where Amundsen-Scott Base is, to avoid worrying about magnetic positioning, magnetic pole movement, global wobble, GPS inaccuracy, etc). Does it matter that the two points on opposite sides of the world are both in constant darkness in midwinter and constant sunlight in midsummer? How does one get a grip on diurnal variations? Also, the two points have different thicknesses of atmosphere between them and the Sun, except for two moments daily. Then they alternate half-daily as to which one has the thicker atmosphere, so there is a solar irradiance attenuation effect not the same as (say) comparing sites along the Equator.
What is really meant by an average temperature at a chosen time at the Pole, corected by station observations up to 1000 km away? It’s a mix of day and night – but at least it’s unlikely to have an asphalt problem.
A Warm Northerly wind at the RP, if continued forward, becomes a Southerly at this opposite point. How does one write an algorithm to correct for wind direction?
Look next at what happens if one goes East from the RP for 1000 km., which is at about 85 deg South latitude. Roughly, one stops at 0 deg longitude, on the Greenwich meridian. The time difference between the RP and this site is a third of a day, or 8 hours. A TOB correction seems in order. The northerly wind example that we used before at the RP becomes a South-westerly if uniformly projected onto a near-planar map projection centered on the Pole. (More probably, in real life, the winds would keep at more constant latitudes and travel around the Pole).
Another complication is cells based on latitude and longitude lines, the latter converging to a point at the Poles. 5 degree grid cells have rather different sizes, with latitude, but this is not the place for an elementary discourse on spherical geometry and map projections.
I am gently making these points because Hans Erren kindly advised of a paper on the India CA thread where the Arctic was used as a location for estimation of the range of interactions between sites. Near-polar regions have particular properties not so similar closer to the Equator, some mathematical, some temporal, some spatial, some climatic – like different albedos.
In the absence of computational code released by Hansen, we have no idea of the sophistication of the adjustments made in polar regions, or whether particular problems were not thought of. We do not know if the 1000 km range derived from Polar regions is valid for ROW.
Unfortunately, the ROW is being fed stories from the USA with no good chance to check them. And they are backed up by Hollywood, so they must be right.
You are now invited to mentally apply the Hansen bias adjustment to Polar regions. I wish you freedom from headaches.
Geoff.
OK. I changed the images to be 600 wide x 300 high and I also TeXified the fractions near the end.
That’s all folks.
Oh yes, WordPress uses xhtml meaning that its very much stricter about closing tags than html. I think I agree with being strict because html to me makes no sense.
Mr Pete:
I think you’ll find it’s so I’d suggest a marble hunt is in order!
so I’d suggest a marble hunt is in order!
re 10:
That’s because at that lattitude coastlines cross the 180 meridian and the application connects them across the front of the picture and not over the backside.
IPCC AR4 uses Robinson.
John A – 🙂 🙂
My only excuse — It’s been a while (17 years) since I actually had to use all this in practice to create the first PC GIS. This discussion is good for scraping out the cobwebs in my brain!
OK, I just made the mistake of going over to Realclimate, and saw this:
http://www.realclimate.org/index.php/archives/2008/02/antarctica-is-cold/
[snip] Hansen’s projection at the top of this entry CLEARLY indicate a dramatically warming Antarctic. [snip-
Re Steve #26 and Hans #33, neither the 1889 Aitloff projection nor the 1963 Robinson projection purports to be equi-areal.
The Robinson projection was popular in the 1960’s, and was the official NGS world map projection until 1988. Y and width as a function of latitude have no mathematical form, and are just defined by a table that Robinson made up that makes the map look nice. His table appears to greatly enlarge the polar regions, so that the gray bands shown by AR4 are in fact part of the projection. IPCC’s team of experts have evidently tried to compensate for this enlargement by graying out an ad hoc slice at the top and bottom, without actually removing this area.
Mollweide and Eckert IV, on the other hand, are actually mathematically derived equi-areal projections (or so I’m told — I haven’t checked either formula myself). Only they or other equi-areal projections should be used by IPCC for such graphs, if they have any pretense of being scientific.
Even if Aitloff were equi-areal, it would have the disadvantage for climate studies that its parallels are not horizontal straight lines, so that the viewer cannot see at a glance how N or S a given point is. In fact, however, it is the “equatorial form of the azimuthal equidistant projection, stretched into a 2:1 ellipse”. Thus, it starts out as equidistant, rather than equi-areal, and then is deformed until it is not even equidistant any more. It may give a pleasing and informative view of the world, but doesn’t seem to fit any exact purpose.
Re #26, 32, I see now what you were getting at, Pete. The Lambert projection you had in mind compensates for the secant(latitude) stretching of the parallels in a rectangular (cylindrical) projection by setting the derivative of the vertical axis equal to its reciprocal, cos(lat). This in fact makes the vertical axis sin(lat). I was not very clear about this in my description of Lambert above. The Sinusoidal projection, on the other hand, just sets y = lat, and lets each parallel be its true length, proportional to cos(lat).
Since I can implement Mollweide and sinusioidal in R and don’t know how to implement Eckert IV, the next time that I draw a world map of something, I’ll try to do it in equi-areal view.
For MATLAB users, I find the warp command the most effective for map projections. I don’t have the code conveniently to hand at the moment but essentially the steps are:
– get a long/lat rectangular image to reproject
– use MESHGRID to create rectangular matrices of long/lat
– apply geometric transform to these matrices
– use WARP to overlay the image
Warp just uses texture mapping, so uses a bilinear interpolation between points, but as long as your long/lat grid is dense enough this won’t matter. What is nice is that this method isn’t limited to 2D projections – you can do 3D projections as well, on to a sphere for example:
WorldImg = imread(‘my_world_map.jpg’);
[x,y,z] = sphere(50);
figure;
warp(x,y,z,WorldImg);
should create an image window with a square map texture mapped on to a sphere, which you can grab and rotate with the mouse. The world map needs to be oriented the right way first, of course, otherwise it will look very odd 🙂 Use axis equal and axis off to make the image look spherical and uncluttered.
Sinusoidal reprojection of rectangular world bitmap in MATLAB:
WorldImg = imread(‘my_world_map.jpg’);
[xdata, ydata] = meshgrid([-180:10:180]*pi/180, [-90:10:90]*pi/180);
warp(xdata.*cos(ydata),ydata,zeros(size(xdata)),WorldImg);
set(gca, ‘View’, [0 90]);
axis equal
axis off
As usual wordpress will make a mess of the quotes!
Since I updated my copy of the GHCN v2.temperature.inv file with the appropriate (x,y) values for the Mollweide projection, I will use that projection in the future.
To be very accurate in terms of area (factor of 1.134 from the best to the worst areas on the map, maximum difference of 4% distortion from place to place)… the (Buckmkinster) Fuller (“Dymaxion”) projection may be the best. On the plus side, the twenty icosahedral triangles make you want to fold it into a real 3-D icosahedral version of a globe (and it is easy to do). On the minus side – it really doesn’t look like a real map when printed or displayed flat.
The American artist Jasper Johns did use such projections to make a prety decent looking map – by hiding the lat long lines and the oceans. Could envision a layer to hide the lat long lines and oceans for some audiences, include them for others.
Wikipedia has a nice write-up (google: “Dymaxion Map” or “Fuller Projection”)- including the Jasper Johns.
Even better, there is a “C” program to convert lat long to x, y for a Fuller Projection. (Google: Robert Gray Fuller Transformations, then select “Source Code for Coordinate Transformations). The University of Toronto Press paper which has the area data is available (I spent $12.00 for it…) on the utpjournals.metapress.com site “Exact Transformation Equations for Fuller’s World Map”
(sorry to reference google searches – I wasn’t sure how to embed links)
In #36 I wrote,
Sorry, Ross and Steve — My gentle sarcasm was just referring to the 619 co-authors of WGI, not the 624 reviewers!
(Somehow Newsweek gets 619 + 624 = 2500 scientists “solidly behind” AR4. In fact, the sum is only about 800 or 900, because of extensive overlap between the two lists, and even this invited list includes many critics.)
Steve: The 2500 was discussed previously somewhere and, as I recall, it was found to include WG2, WG3 and the Synthesis Report, but I’m not sure.
The 1772 Lambert Equal-Area Azimuthal projection, mentioned by Gary on the earlier thread, is another valid projection. It doesn’t preserve N-S, but does provide interesting alternative perspectives, with good views of the polar regions when centered on the Equator:
It’s also relatively straightforward to compute.
Here’s an equirectangular graph Steve did on the earlier thread on Hansen and Hot Summers:
For small regions, areal distortion in equirectangular graphs is not a big issue, but the US is large enough that Texas is not getting its fair share here, while Maine, Seine rain and all, is overrepresented.
I’d suggest that such country or regional maps should instead be presented in the Lambert Cylindrical Equal Area projection illustrated above in the post. (The original link didn’t work, but this one should).
The standard Lambert Cylindrical has vertical scale equal to horizontal scale at the equator, and hence mashes higher latitudes. There is no reason, however, that it cannot be calibrated so as to give equal vertical and horizontal scale along any reference latitude desired, so as to preserve shapes at that latitude. In the case of the US, I would suggest about 38 degrees.
10 degrees on the horizontal axis of Steve’s graph are about equal to 5 degrees on the vertical axis. This preserves shape at 60 degrees N (Anchorage or Oslo), but causes excessive narrowing at US lower 48 latitudes.
#43 – Something like NASA does with it’s J-Track 3D really would be cool.
Good to see some people have time to reinvent the wheel.
For all the others there’s Rich Pawlowicz’s M_Map package in Matlab :
http://www.eos.ubc.ca/~rich/map.html
which does support all sorts of equal-area (AND equi-areal !) projections, in particular the Mollweide :
http://www.eos.ubc.ca/~rich/map.html#e4
These mapping conventions do matter a whole lot. I had a collaborator who contended that climatology’s progress was delayed by 50 years because people were using polar stereographic projections for, say, Northern Hemisphere climate, which had the unfortunate effect of masking that much of the interesting dynamics originates in the tropics.
I fully agree that Mollweide gives a much more fair view of a global field – aside from its shape being more than appealing to a Rugby fan.
Julien writes (#46), “Good to see some people have time to reinvent the wheel.”
What a pity then that NASA and IPCC are still dragging sledges!
PS: Re #36, make that Aitoff, as in #26, not “Aitloff” as I had it.
Re #26, 36, There’s also an equal-area Hammer-Aitoff projection that looks a lot like Mollweide, except that the lines of longitude curve as in Aitoff (#26). It does not distort Alaska as severely as Mollweide does, but IMHO that is a big price to pay, in a climate context, for loss of N-S monotonicity. It’s supported in the UBC package Julien recommends in #46, which is where I learned of it.
Note that Mollweide etc can easily be “interrupted” so as to reduce shape distortion. However, this greatly increases distance distortion (counting the gaps), and so is counter-productive from a climate point of view.
Julien, no one is “re inventing” any projections. I don’t think that it does any harm to take note of the projections in IPCC usage. It’s not a big point, but, as you say, failure to attend to this seemingly small issue can cause some misconceptions.
Nor is there any harm in those who understand these things making it easier for those who don’t.
Re #49
I think JEG is taking a pop at me for posting up MATLAB code to perform a reprojection. What JEG doesn’t realise is that a considerable amount of the toolbox he links to simply performs the exact same task as the built-in warp function. (WARP only became available in v6.5, whereas the toolbox he links to was written for MATLAB v5). So even with the toolbox, you still have to write most of what I did in #39, just using less efficient, less portable, less maintainable non-standard functions rather than the built-ins.
That said, it took me probably less than a minute to write the code in #39. How long would it have taken me to search for that toolbox, read up on it, download it, and use it? Considerably more than a minute! And then I’d still have to write most of #39…
I guess it is a good job someone has time to spend all day surfing the ‘net rather than doing real work and properly exploiting the advantages of the latest versions of MATLAB.
Gosh this is just like England vs. France at rugby all over again. 14-9 ring any bells here? 🙂
Postscript: Of course, Rich’s toolbox, once installed, gives you quick (ish) access to several different projection schemes. If your maths isn’t too strong, or your MATLAB is a bit out of date, it would save you a considerable amount of time. You’d still be left with clunky outdated code though.
Re #46 JEG
Dr. Emile-Geay,
Having formerly spent a couple of years instructing students, I wonder what your philosophy on instruction is? Do you believe that a simple recitation of fact is sufficient? Or, would you prefer that your students actually learn how to derive the fact (and any underlying basis for such derivation)?
My approach has always been to teach them to determine the facts for themselves, including following false trails to dead-ends, if necessary, albeit with guidance to help recognize a dead-end. Telling the student a priori that their line of investigation leads to a dead-end is not particularly instructive, in my opinion.
I find that philosophy mirrored, to a large extent, by Steve’s blog; so I find your criticism a bit confounding.. I certainly find “appeals to authority” less than compelling, and would encourage you to refrain from the disparaging commentary and help us to understand the path that Climate Science and paleoclimatology have taken to obtain the results that you (and your colleagues) have presented.
If this includes revisiting projections, so be it. Not everyone has your years of training, knowledge and experience and I wish you wouldn’t begrudge us the opportunity to learn some of it, and maybe, even, there is some bright mind reading this thread that will invent a new, possibly better, form of projection.
I encourage all posters to keep the discourse lively, but to refrain from disparaging commentary which has little educational value (or any other value for that matter).
Hu
Useful thread.
In the special case of Hovmoller diagrams that post degrees latitude on the x-axis and time on the y-axis, there is clearly a distortion with latitude as measurements in the polar regions are given equal weighting with lower latitude measurements.
Instead of plotting Hovmoller diagrams with latitude in the range 90S to 90N as a linear degree axis, a more appropriate approach might be to plot sine latitude on the abscissa in the range -1 to +1. This approach would locate lat 30S at -0.5, lat 30N at +0.5 & Lat 60N at +0.866 etc. This scaling would then provide a more appropriate visual match to the global variation of surface area with latitude.
Describing and Analyzing Graphs
Giovanni Plot Types
I remember reading a claim that much of the increased global temperature we’ve seen over the last 30 years is in fact an artifact of the projections used that amplify the relative area of the northern regions. Anyone know any more about this and whether this is in fact true?
Re #43: Rotating the Lambert Azimuthal Equal-Area projection to the meridian of either Delphi or Alexandria (ancient contenders for the Center of the Universe) would bring Indonesia and Australia into the picture better, and give a more balanced World.
In #48, I said, “except that the lines of longitude curve as in Aitoff.” Make that latitude. Whatever…
Two factors beyond dispute, then an opinion.
1. You cannot make a planar undistorted map of the globe that has meridians parallel e.g 44 Hu. You can make a map of a small part which approximates this. How small? Depends on the use. Risky to go beyond a kilometer mostly. We would survey grids of white pegs according to curvature (The Australian Map Grid, AMG) and there was a definite, visible curvature over a few hundred meters.
2. It is instructive to rotate a globe of a usual Mercator type projection placing the Poles on the present equator. Add a 5 deg by 5 deg grid as it would look on a normal Mercator. Then plot the existing climate stations to see how dense they are. Indisputable fact: You cannot interpolate through empty grid cells with anything better than an inferred mathematical guess.
Opinion: Global policy on climate change should not be made when huge areas have no better than inferred guesses about data.
#56
Always.
I was thinking any of the Malwide / Robinson projections might look better if the poles of the projection were established north west of Japan and southeast of Chile — that is, in otherwise fairly empty parts of the globe.
For fun. When the Shah ruled Iran, we did an airborne geophysical survey of a significant part of the country, flying proton magnetometers at 80 m terrain clearance and using Brit milspec nav radar range-range systems (“Tans”, before the advent of SatNav). The authorities demanded we produce maps that had North-South lines parallel to the edges of the map paper, but also so that distances betwen places on the ground were correct and could be scaled by ruler. So we had an educational job with I hope we did with more grace than JEG above.
We also did tracking camera flight path recovery, with an 8 mm movie camera in the belly taking a snap every second. Features were then accurately identified on high altitude aerial photos and the flight path plotted. This is a scientific procedure sometimes called “confirmation” or “replication” whose use seems to have decreased in recent years, to be replaced by immense faith in computers that work with 64 bits, because 64 is more powerful than the 8 bits that some of us started with.
Such was the military paranoia that the first lot of censored 8 mm film we got back had every recognisable feature cut from it. We got a cardboard box of short shots of sand dunes and a camel.
In the course of this work – in the late 1970s – we developed Fortran software for the accurate plotting of base maps from first principles at any scale and at any place in the world, with several earth model shapes. Quite a few possible projections were incorporated, but luckily we did not go on to survey in Polar regions. We had enough problems with understanding weather and climate where we worked.
It is not necessarily intuitive for a scientist or engineer to understand spherical map projections and conventions. Clearly, those maps commonly in public use which give huge Polar areas are distorting the impressions of the naive or those uneducated about the nuances.
Gary says:
I agree – since NASA has the data, why couldn’t they incorporate the anomaly information to the surface of that globe?
And of course, this being Valentine’s Day, we mustn’t overlook the equal-area Cordiform map of Orontius Finnaeus (1494-1555):
This is essentially an equidistant polar projection, except that instead of each line of latitude being stretched to go entirely around the pole, it only goes half its true length on each side of the central meridian. As a result there is no size distortion, albeit considerable shape distortion (“shearing”) toward the edges. NS and EW distances are actually true when measured along the curving lines of longtitude and latitude.
The oversized Antarctica is not due to the projection, but just to the pervasive 16th century notion that there was an Antarctic continent much larger than the actual one.
This is in fact an excellent projection that should rank high on any equal-area list.
Pouncer (#56) writes,
This would be interesting to try, but the globe has to be split in back from pole to pole, so it would also help to have a great circle connecting the two poles that is entirely (or almost entirely) water. From say 165E, 30N to 15W, 30S you have to cut a lot of land no matter how you do it.
this one?
Try, try again:
Wikipedia article on Orontius Finnaeus with Cordiform Map
That looks like a version of the Bonne projection (an example shown below with parameter 30). At parameter 0, it looks to me like the Bonne projection goes to the sinusoidal. THe one shown above looks similar to parameter 45 or 60 or something like that.
On second thought, NS distances along meridians do get blown up as you move away from the central meridian, but it should still be equal-area since areas of thin annuli are preserved. EW distances can be measured with a protractor centered on the N Pole.
(In my first attempt at #61, I tried closing my tabs XHTML-style, with a / before the >. However, the comment window seems to recognize the HTML closing > better. One fluke of WORDPRESS is that you can’t use the .LT. sign, since it thinks it is the beginning of a tag that continues until it sees a > sign, so you must either type X .LT. 3 or go into TeX mode. However, X > 3 is OK, since > means nothing to it unless you are already in a tag.)
It seems that the Cordiform projection was fist invented by a Johannes Stab in 1500, and then refined and promoted by Johannes Werner (1466-1528), whence it is also known as the Werner Projection:
Again, if the globe were turned a little clockwise, Australia would be brought into the picture better, and the landmasses more symmetrically surrounded by ocean.
RE Steve #65, the Bonne Projection, named for Rigobert Bonne (1727-1795), was in fact invented by Sylvano in 1511. It nests both the Werner/Cordiform (which has no shearing at the N Pole) and the Sinusoidal (which has no shearing at the equator), to have no shearing at a selected standard latitude. When this is set to 45 degrees, the following results (I hope!):
Very nice class, but again it could use a little clockwise rotation.
Hmmm …
Why not make the leap into the 21st century and make a 3-D map projection animated to rotate the image like Google Earth et al.
While I’m at it, here’s a Robinson Projection for comparison to the IPCC AR4 Robinson maps in #10 and 20-21 above (ID’d by Hans in #33 as Robinson):
This projection was popular in schoolbooks of the 1960s-80s, but obviously makes Greenland and Antarctica way too big. As noted in #36 above, IPCC has apparently tried to visually compensate for this by arbitrarily slicing a few degrees off the top and bottom, and representing these in neutral gray. It’s too bad this “climate science consensus” is clueless to the many equal area options that have been circulating since at least 1500.
#70. Good question – here’s something interesting on animation of statistics for R users:
Click to access animation.pdf
Coming full circle to Hansen 1988, here is a comparable view of Earth in the NASA-GISS or Equirectangular Projection, aka plate carée, which was attributed by Ptolemy (c 150 AD) to Marinus of Tyre (c. 100 AD):
Note the hugely inflated polar regions. Ptolemy himself preferred the far more advanced (but still not equi-areal) Conic projection.
As they say at NASA, “Whaddaya expect, Rocket Science?”
re: 66
Try using ampersand-ell-tee-semicolon instead to get the .LT. symbol (e.g. <)
scott
I inadvertently set the width wrong in #73, with the result that shapes are undistorted at a reference latitude of about 41.4 deg. For an equatorial reference latitude as used in Hansen 1988 etc, the aspect ratio should be 2:1, as follows:
Re #70
For MATLAB users, my code in #38 (that JEG didn’t like very much) does just that. It projects the map onto a sphere which you can grab and rotate with the mouse.
You can then create animated .gif using the ‘WriteMode’, ‘append’ parameter of imwrite or an avi using the avifile commands, although not an image a third party user can themselves control.
Of course, this is not very helpful for non-MATLAB users. Sorry folks 😦 There might be an ActiveX control kicking around that does that, or maybe someone with Flash skills could do it?
That’s the bummer about using a proprietary software package vs. a library compiled in something open-source such as C or R. The other bummer is that the proprietary packages aren’t “standard” in the same sense as C or R, and as a result, incompatibilities exist between releases. Usually with MATLAB they give you a warning when something is about to be changed, or outmoded, but releases that are more than one major revision apart (e.g. version 5 to version 7) may simply result in an error. I’ve had compatibility issues between versions 5 and 7, which is why I mention those in particular (and if the package JEG referred to really is for version 5, updates may be required to work with version 7).
Mark
RE 76. Spence I got a huge laugh out of JEGS attempt to criticize you.
It was classic.
for animated gifs I use Mirosoft gif animator (free)
Here is an animation I prepared with GMT (aerthquakes in the vicinty of Greenland by year.
horrible spelling mistaks 😉
OK, for fun and removal of cranial cobwebs, I’m bringing myself back up to speed on projections 🙂
A few notes on projection accuracy:
* Fundamentally, we’re dealing with conversion from 3D “paths” (bounding curves described by infinite-precision real numbers) to 2D pixels (theoretically, square boxes of light or color). There’s not only areal distortion involved but also angular distortion as well as challenges introduced by antialiasing effects, etc.
* Bottom line: NO projection will always get everything visually correct, even for display of areas. You can optimize the various factors for a given situation, but change the parameters a bit and the accuracy is lost.
* An example of the kinds of issues that will always plague us: look at any of the displays above. The smallest area represented is a single pixel. Even assuming perfect displays and eye reception, these maps are displayed as no more than about 300 x 600 pixels, vs the earth at about 20k x 40k km. I.e. the pixel dimensions we’re viewing each represent 65km or more at the equator. That’s a large areal error factor in itself, and is compounded by angular errors.
* Turns out that the various equal-area projections, AND the projections (such as Robinson) that use compromises to come close, are all reasonably similar at the resolutions we’re dealing with — they are within an order of magnitude of the correct values… and that’s about as good as you can get. Other than avoiding blatantly bad (unprojected, Mercator, etc) choices, I wouldn’t worry about niceities of projection selection for simple display purposes like this.
I googled a bit and found an interesting analysis paper here.
Table 2 shows results that might be surprising to some:
* All the equal-area projections are accurate for large scale maps (e.g. 16km pixels and below)
* At 25km pixels, Mollweide significantly under-represents areas, while Robinson’s accuracy improves to be approximately correct (probably due to its reduced areal distortion)
* At 50km pixels, all the projections under-represent areas; Robinson is (slightly) closer to correct than the other projections discussed.
* (They don’t analyze for anything smaller scale than 50km pixels)
Again, I’m not arguing for one or the other of these projections. Simply that we shouldn’t get too picky about such things due to the inherent inaccuracies at the scales we’re dealing with. Choose any of the reasonably good projections and you’ll do well — certainly better than unprojected results!
(By the way, slash-before-‘>’ is xhtml, the modern way of doing html 😉 )
This is the map projection bible:
Snyder, J. P. Map Projections–A Working Manual. U. S. Geological Survey Professional Paper 1395. Washington, DC: U. S. Government Printing Office, 1987.
http://onlinepubs.er.usgs.gov/djvu/PP/PP_1395.pdf (yes, online 394 pages!)
see also
http://www.galleryofmapprojections.com/
Mr. Pete (#81) writes, paraphrasing the Usery & Seong paper he links,
I can see that Mollweide will distort areas — a 25 KM square on the ground may at one point appear to be a 1 pixel square, while somewhere else it may map to a diagonal area 10 km wide and 62.5 km long on the scale of the first pixel, and hence end up as a small portion of several pixels. Depending on how the pixels are assigned to the data (by NW corner? by Center?), this could cause some local distortion or even Moire patterns. But how could it systematically under-represent areas if it’s mathematically equi-areal?
When plotting detailed data at 300X600 pixels, a lot of the data points are going to get lost. But as long as each pixel is assigned the data point nearest its center, how is this going to over- or under- represent areas on average? If you really want to provide more resolution, provide a link to a bigger picture. Thus all the Wikipedia pictures I displayed above can be blown up to several screensful by going back to the article and clicking on the image a few times. If you want to scrutinize the polar region, say, you just have to use the scroll bars to get it on your screen. I just shrank them to blog-size (about 300X600 or 400X400) for the convenience of readers, whence the grainy lines of latitude and longitude. Likewise, if you’re going to print out a wall poster, do it from an appropriate resolution image.
Robinson has more, not less, areal distortion than Mollweide etc. Its advantage is in shape distortion, and in particular shear, so that assigning pixels to data is less of an issue. But how can it become approximately correct areawise just by pixilating it?
If you’re going to print your map on a standard page as part of an article, there could be an advantage to the squarish projections (eg Lambert Az or Werner/Cordiform) over the rectangular ones (eg Mollweide, Lambert Cyl.), simply because they get more height per unit width, and therefore will show more resolution. But still you’d want to start with an equal-area model.
That may be true in the post window, but in the comment window slash before > doesn’t work for img src. Omitting the slash is how I got the Werner/Cordiform image to work in #68 above.
Wow… some great news. I was about to comment that the gold standard of map projection software libraries is from Mentor Software. I googled, and found this announcement:
AutoDesk is preparing to donate the entire Mentor projection library as Open Source! That is extremely wonderful. Mentor’s code is the only I’ve seen that provides extremely accurate, fully reversible projections. (I.e. you can project to-and-from a projection and get your original data back, as closely as can be managed.)
For areal representation accuracy: it’s all in the niggly details. Choosing how to convert data between two spaces is quite tricky. Not as simple as pulling a value from the center of the projected source. Among other things, we’re not dealing with infinite-precision math… and it actually matters in cases like this. It’s easy to end up with rounding effects that impact the displayed result. Anyway, I think I’ve gone about as far as I need to on this. I don’t *really* want to revisit the niggly details! That was a previous life 😀
From Wikipedia:
The Peters projection map was featured in the United States television drama The West Wing (season 2, episode 16), in which the (fictitious) Organization of Cartographers for Social Equality is given access to the White House Press Secretary due to Big Block of Cheese Day. Dr. John Fallow (actor John Billingsley) explains why the President of the United States of America should champion the use of this map in schools, because it correctly represents the size of the countries and therefore gives due prominence to countries in less developed parts of the world that are otherwise under-estimated.
The Peters projection is ugly.
http://geography.about.com/library/weekly/aa030201a.htm
snip
Maybe this is a dumb question but when these grid calculations are made surely the grids are defined in a 3 dimensional inertial coordinate frame…right? Its only when the results are presented that we get into a debate about what sort of spherical to 2-D projection most clearly conveys the information. ???
Re #78
Thanks mosh, I have whinged a bit about JEG’s response here; although in one narrow sense he is right (if you just want to have a play with lots of different projections, you can’t beat downloading a library); he completely missed the point that if you have a slightly deeper understanding of what you are doing, you can do surprisingly powerful stuff just with the MATLAB command line (beyond what the mapping library offers).
There was a guy who I worked with some time back, and whenever given a tricky maths based task, he would immediately go to the web and look up someone who had already written the code. He got away with this once or twice until he was given a task that he couldn’t find; then he was stuck. JEG’s comments just remind me of that.
Incidentally, when messing about with this stuff in the past, I’ve tended to use Dave Pape’s maps, located here:
http://www.evl.uic.edu/pape/data/Earth/
Some very nice high resolution maps which are perfect for warping in MATLAB 🙂 And with the other tools, of course.
I wrote to Tom Minka, the maintainer of the R mapproj package as follows:
> Thank you for the excellent R package. I have a couple of questions
> which I’d appreciate some help with and may useful to you in any
> iterations. 1) In the map(“world”…) function, I get annoying and
> distracting horizontal lines around 60N e.g. example below. This
> occurs in different projections. 2) the white borders around the
> image are much bigger than I want and I can’t figure out how to shrink
> the margins; 3) the outer boundary isn’t marked. With some
> experimenting it seems to be at about 174.8-174.9W – a sensible
> location visually. I think that it would be a good idea to actually
> show the edge or at least include an option. Cheers, Steve McIntyre
>
He promptly responded as follows:
re 88
This depends on the model, I certainly hope they do consider geometric effects on global models.
RE 89. reinventing the wheel is a most useful excercise. Making a fetish of novelty
leads to hockey sticks and other freaks of nature.
I really do like JEG. he likes Tom Waits; he writes well ( read his papers); he’s not
afraid of a fight; and in the end he is a civilized human being with a sharp tongue.
He’s like me, except I’m right and he’s wrong.
I think this thread is fascinating, informative and fun. Its exactly the sort of subject best covered in blogs.
I don’t understand the carping about it at all.
re 93: It’s why I come here. I find it endlessly fascinating to watch people from different disciplines
come at a problem. I Don’t care so much about “the answer.”
Here’s a nicer version of the Lambert Cylindrical Equal-Area projection, in its standard equatorial form, in which the vertical and horizontal scales are equal along the equator:
With this scaling, the aspect ratio is pi:1, so that it shows much less detail on average than the Equirectangular projection, whose aspect ratio is 2:1, and which shown in #75 above with the same width.
However, this disadvantage can easily be corrected simply by stretching it vertically until its aspect ratio is also 2:1:
[Can’t get rescaling in HTML img tag to work here]
With this aspect ratio, the vertical and horizontal scales are equal at a reference latitude of 40.08º N or S. As in Mollweide, Eckert IV, or Hammer-Aitoff, the vertical scale is not constant, but is equal on average to the constant scale along the equator. Each hemisphere is represented by a perfect square.
Many other reference latitudes have been proposed for the Lambert Cylindrical projection: 30º (Behrmann), 37º04′ (Cranston), 37º24′ (Trystan-Edwards), 37º30′ (Hobo-Dyer), 45º (Gall-Peters), and 50º (Balthasart). But for some reason no one has ever before thought to simply make the globe as high as each hemisphere is wide. I suggest that this new variation be called the Isometric Lambert Cylindrical Equal-Area projection because of its equal average vertical and horizontal scale property.
If the Equirectangular projection is to be compared to an area-corrected rectangular projection for contrast, this Isometric Lambert is the natural candidate because of its equivalent aspect ratio. It would also work well for individual country or region maps near 40º N. or S., eg the US as in #44.
Hans (#87) rightly disparages the overhyped Gall-Peters projection, with its 45º reference latitude and 1.57:1 aspect ratio, as “ugly”. I find the Isometric Lambert to be a lot better proportioned than Gall-Peters, though of course not as nice and curvy as the Mollweide or Hammer-Aitoff.
Incidentally, the very nice graphs I have been displaying were contributed to Wikimedia Commons by “Mdf”.
There’s a nice Java Applet at http://commons.wikimedia.org/wiki/User:Mdf that allows you to interactively project the globe from any direction in a great many of these projections.
Using it with the Lambert Azimuthal Equal Area projection (#43), for example, it may be seen that a prime meridian of about 10º E gives a nicer balance of ocean around the landmasses, and at the same time doesn’t make NZ look like it’s somewhere south of Antarctica!
Unfortunately, there’s only one Bonne projection, and no cordiform.
Hu, I didn’t see the applet, only pictures uploaded by the user named MDF.
Re 95: Actually, some of you might recall, I presented McCulloch’s “Isometric Lambert Cylindrical Equal-Area projection” as a better way to present temperature anomaly data on this site a while ago. It was the best solution I could come up with. I wrote a program in c and openGL to transform a Straight Cylindrical Projection into a ILCEA :). SCPs distort the data too much. Now that this better representation has a name, we might agree to use it. Anyone know how to add this to R?
Re 96, 97:
Sorry, wrong URL —
http://www.uff.br/mapprojections/mp_en.html
RE John Bell, #98, Indeed John has already invented “my” Isometric Lambert wheel, as JEG would say. See the links John provides in his comment #88 on Thread #1100, 1/23/07. He compares an equirectangular map with the poles ablaze to a benign “Isometric” Lambert Cylindrical projection. #95 above answers his question in that thread about Behrmann vs. Gall-Peters.
Perhaps Julien can tell us if someone implemented this idea before John. It’s simple enough, but Snyder’s 1987 tome (see Hans #82 above) doesn’t seem to mention it.
Also, in #79 of the earlier thread, Willis Eschenbach dramatically showed a Mollweide projection of other data that Steve had presented Equirectangularly in #15 of that thread. The first illustration of that thread, taken from an article by Mears and Wentz, appears to be Mollweide.
Re #98, 101, here are John’s maps for comparison. First, the distortionary c. 100 AD Marinus-NASA Equirectangular projection:
And then (I hope), the same data, with the area-corrected “Isometric” Bell-Lambert Cylindrical Equal Area projection:
In all fairness to the real rocket scientists at NASA, the Equirectangular may be convenient for tracking satellites at a glance. It just doesn’t work for climate studies. It’s too bad Darrell Huff isn’t still around to write a sequel to his classic How to Lie with Statistics, How to Lie with Cartography!
tool:
sphereview (free!)
http://www.triusinc.com/sphviewanim.htm
With this tool you can wrap a rectangular map on a spinning globe.

see also:
ice age globe
citylights globe

ocean temperature anomaly

second tool:
with Microsoft gif animator (free) you can edit the animation into a repeating loop.
here is Hu’s map in sphere view:

I am not sure if the “Isometric” Bell-Lambert Cylindrical Equal Area projection is still equal area: see page 76-77 in Snyder(pdf page 85-86) for properties and discussion of Gall-Peters and Behrmann.
Click to access PP_1395.pdf
Re Hans, #105,
Snyder concurs that Gall-Peters, Behrmann, etc, are equal-area. They have to be, because they are just dilations of the standard, or “equatorial” Lambert Cylindrical Equal Area projection. Dilation to a more natural 2:1 aspect ratio, which I’m calling “isometric” for want of a better word, has the same property, just a different standard parallel (40.08º).
RE 104, cool image, but the underlying map is in fact due to John Bell, not me. I merely copied them here in #101 from his post early last year.
Incidentally, the Wikipedia article on Lambert CEA was missing the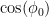 term that Snyder gives in the formula for X. This is required because you not only have to stretch the map vertically when you change the standard parallel, you also have to compress it horizontally by the same amount. (Or alternatively, leave one axis unaltered and change the other by the square of this factor.) I changed it last night, and no one has complained yet!
term that Snyder gives in the formula for X. This is required because you not only have to stretch the map vertically when you change the standard parallel, you also have to compress it horizontally by the same amount. (Or alternatively, leave one axis unaltered and change the other by the square of this factor.) I changed it last night, and no one has complained yet!
The informative graticules in #95 and #75 above (and other graphs) didn’t come through well. The following were reduced in Photoshop instead of using HTML height and width settings.
Standard (Equatorial) Lambert Cylindrical Equal Area:
Isometric (2:1 aspect ratio) Lambert Cylindrical Equal Area:
NASA/Hansen distorted area Equirectangular:
What you call “NASA/Hansen distorted area Equirectangular”, is called Plate Carrée in the cartographers jargon.
It’s the most straightforward way of plotting lat long. (It’s not intent, it’s lazyness to plot equal area)
http://en.wikipedia.org/wiki/Plate_carr%C3%A9e_projection
So it does have some benefits…
It turns out that GISS does offer an alternative to the area-distorted Equirectangular or Plate Carrée projection, but one that is even more area-distorted in favor of the poles!
At http://data.giss.nasa.gov/gistemp/maps/, there is a menu that allows you to obtain a map of temperature anomalies with selected parameters and a choice of either of two projections: “Regular”, i.e. the area-distorting Equirectangular, or “Polar”. The page does not say which of several Polar projections this might be, but here is the output for 1/08 using the default settings for all the other parameters:
By eyeballing this relative to the several Azimuthal projections supported by the Map Projections site of Rogerio Vaz de Almeida et al (including the Lambert Az. E.A), it would appear that this is a Polar Orthographic projection, in other words, a view of the globe when viewed from outer space infinitely far away, with no parallax distortion.
It does, however, generate serious area distortion, and from this polar aspect, the equator is in fact infinitely compressed. This is far greater than the merely finite area distortion of the important tropical region in the “GISS-Regular” projection. Here is a very obviously, and equally, distorted view of the globe from over the equator using this same projection:
(Source: Wikipedia Orthographic Projections article)
On viewing the GISS Polar map, another oddity of GISS-data emerges: If you circumambulate either Pole on a 10-foot tether, the temperature will change dramatically as your latitude changes, even though you are essentially in the same spot. Evidently GISS takes its “Regular” projection seriously, and believes that these are widely separated locations.
Here is another try at the equatorial orthographic image from the Wikipedia Orthographic Projections (Cartography) article:
RE ChemicalEngineer (#41), in Junior HS and HS, I was a big fan of Bucky F, and even heard him speak a few times at the University of Colorado’s United Nations Week. His icosahedral Dymaxion Map is ingenious and thought-provoking (and nearly equal-area), but unlikely to ever catch on. Here is an animation of the land-mass version of it from the Wikipedia article (I hope):
Hu Please don’t get to carried away with this topic. You may favour a new map projection that is not part of the standard packages, but this introduces the practical problem that few people can generate them.
I suggest therefore for global views to stick to Mollweide equal area and for polar views lambert azimuthal equal area.
So Isometric (2:1 aspect ratio) Lambert Cylindrical Equal Area is indeed correct, but not unfortunately not practical.
I have been teaching map projections for ten years now and the majority of earth scientists is simply not aware of map projections, let alone that they can be convinced to use uncommon ones.
And Orthographic polar is really not that bad, after all it’s the same view you have when looking to a globe on a table.
Hu McCulloch,
This distortion can be avoided, if you reduce the “Smoothing Radius” (interpolation?) from 1200 kilometers to just 250. In this case you can also see, that the data base is very sparse…
FWIW as far as practical goes: the simple cylindrical equal-area (adjusting latitude) is eminently practical. In our mapping systems, we simply set the center latitude to the displayed map central latitude, and adjusted as-needed for display. At small scales, you can simply change the aspect ratio of the data display. At large scales, y’gotta do the real projection, but a single trig function is fast enough that on-the-fly projecting works nicely.
I agree with Hans: projections are fascinating but mostly an interesting curiosity to a fraction of the public. The projections needed and used for land-use analysis (GIS, topo maps, etc etc) are much more “boring”.
If we could get the global climate community to standardize on one or two simple but accurate world-display projections, that would be a nice outcome.
Gerhard H.W. writes in #113,
The bug will not be obvious if the smoothing radius is small enough that no stations are within this radius of either pole. But the bug is still there.
And given that many people probably will use the larger smoothing radius, this error gives the public the false impression that the polar regions are much more volatile than they really are. (Quite aside from the false impression, already generated by the area-distoring projections, that they are much more important than they really are.)
re 144:
The biggest point against any cylindrical projection is that the north and south poles points are stretched out to a line of 40000 km..
Only if you believe that an equal-area map is also equidistant :-)… giving good scale/distance feedback helps people visualize the reality of a map.
I do like Google Earth because of this. A good visualization tool for areal themes like this would be to wrap the data onto a virtual globe, and accompany with a pie/histogram showing the relative global area assigned to each color “bucket”.
Re #112, 114, 116, 117, I agree that we should promote one map, and that should be Mollweide.
Nevertheless, if NASA insists on thinking “inside the box,” we should be prepared with the Lambert CEA (preferably in John Bell’s isometric 2:1 aspect ratio) as an “area corrected box”. If NASA offers an orthographic polar, we should be prepared with the Lambert AEA as an “area corrected polar”. If AR4 pulls out the schoolbook Robinson, which stretches the poles out to half the length of the equator or so, we should offer Eckert IV as an “area corrected pole-stretched” projection.
As MrPete notes, it is trivial to stretch Lambert CEA out to the “isometric” 2:1 aspect ratio — mathematically, just multiply y by pi/2, or if the graph is already drawn, just change the image height in Photoshop etc (deselecting “Constrain proportions”), as I did in #107 above.
Incidentally, Mollweide has a very nice unipolar aspect. Using http://www.uff.br/mapprojections/mp_en.html, turn the projection so that the central meridian is 30 deg. W, then drag the N Pole down to the centerline. The Arctic is then intact, with the Americas on one side and Afro-Eurasia on the other. This projection would also work well turned vertically in either direction. Unfortunately, this splits Antarctica in two, but for a penguicentric viewpoint, you can instead just drag the S pole to the centerline.
To get both poles in view (“bipolar”?), the best option would be to do each hemisphere in a Lambert AEA projection, then place them side by side, touching at a common point.
It’s unfortunate that the animated GIF of the Dymaxion projection doesn’t pause on the unfolded aspect. Does anyone know how to do this? (I’m not suggesting that we actually use this projection, but note that it does sort of have the same layout as the polar Mollweide described above!)
In Microsoft Gif animator, set the duration of frame 75 to 3 sec.
What is all the fuss about? There’s little gain in arguing for one projection over another. Those schooled in geology and mining and surveying learn to think in 3D anyhow and so can you. It’s not the prettiness that matters, it’s the accuracy and from the accuracy, the ability to discern new insights. e.g. an early series of maps showing polar weather station coverage (or lack thereof) would have been an early alert to a big problem, namely guessing interpolations over many grid cells. And choosing inappropriate grid cells.
Computer science has numerous ways of handling data from the globe and into the sky (or down). Economic geology has specialised in getting orebody grades correct over 3 dimensions from limited data. Off the shelf mine grade packages should be directly applicable for computation of climate data, no matter what pretty shape you favour. They are carefully designed to derive the best answer from the available data and to tell you when and where you need more.
My favourite interpolation method for irregular distributed samples is Kriging, this gives you also an error estimate map which is severely lacking in climate anomaly maps. Geostatistics in general is poorly used.
Re #109, 113, 115, I’ll concede that the polar discontinuity effect is probably not an actual bug in the NASA program. Such an effect could arise if the top 5 degrees say are chopped into a few pie segments, and each segment assigned the average temperature of the station(s) within 1200 km. If each segment turns out to be barely 1200 km from a single station, it will then be assigned a temperature that could be very different from that assigned to its neighbors. Indeed, if we follow Gerhard’s advice and select 250 KM smoothing, we see that there’s really nothing up there to speak of.
But it’s still a telling quirk that arises from the “gridding” approach favored at NASA. I can envision a smoother technique that would take into account a continuous model of covariance based on the data Hans shows in his Comment 83, on the Historical Station Distribution thread by John Goetz that started this discussion of projections.
This would give a point estimate of temperature everywhere on the globe, though with a calculable uncertainty that would naturally be very large where the data was sparsest. Such a “spatial autocorrelation” model used to be relatively difficult computationally because of the huge covariance matrix, but I doubt that that would be a big problem today.
Perhaps the Kriging mentioned by Hans in #121 (a mining technique discussed here by Steve on occasion) gives similar results, though I haven’t studied it yet.
Anyway, in response to Geoff #120, even if the bottom line is just a global temperature anomaly number, it really helps to be able to visualize the data on an equal-area map in order to understand what the computational issues are. And having a couple of alternative equal-area projections in one’s toolkit can enhance this understanding.
Re #119, thanks, Hans! This is a fun projection to contemplate. It gives the connectivity of the unipolar Mollweide aspect I mentioned in #118, without the extreme shape distortion, and with very little area distortion.
Re #113, #122, compare this 250-km smoothed NASA graph to that in 109:
NASA’s Orthographic Polar projection greatly exaggerates the area of this region, for which the data is in fact quite sparse!
Re sparse data:
One of my biggest battles over the years has been, and still is, to nurture an appreciation of the value of “I dunno.” Demographers, scientists, etc all have an innate desire to fill in the blanks, whether by interpolation, model-building, or whatever. We tend to assume that a nice straight (or nicely curved) line/surface fills in the gaps between our measurements.
Yet more often than not, our assumptions turn out to be false. People are singularly bad at predicting significant future events, and also at filling in the gaps of real-world observation.
Hu’s most recent polar maps are largely “Unknown” data values. I think that’s *fantastic*! Some advantages of highlighting the unknown:
* The “known” data is more believable in the context of admitting what we do not know.
* People will be encouraged to fill in the gaps. Whether students, policymakers or other scientists, it helps
to admit “this is all we’ve got, folks — please help make it better!”
* Spurious analysis can be more easily avoided. The above maps represent very little oceanic data. Other climate attributes are better known in the oceans (say, seafood harvest tonnage). This map demonstrates the fallacy of performing an oceanic-context analysis of the data. You’d actually be comparing a known to an unknown. If all the unknowns were filled in by interpolation/modeling, you’d easily be walking down a fallacious path.
The same goes for highlighting realistic confidence intervals in our graphs and models. If they aren’t good enough to tell us much — let’s admit it with honesty and humility!
There’s tremendous value in promoting what we don’t know.
Re MrPete #124, I fully concur.
However, it now occurs to me that there is an easy way to combine point estimates of temperature anomaly at every point on the globe with an indication of the uncertainty of most of those estimates, simply by using color, which in fact is not just 2 but 3 dimensional!
NASA wastes this potential information by using a one-dimensional temperature scale that runs, from cold to hot, violet-blue-pale green-white-yellow-orange-red-brick, with only an on/off indicator of confidence (color versus gray).
Temperature and confidence could easily be represented simultaneously and in detail simply by using hue (at full saturation) to indiate tempurature, and then luminosity or “depth” to indicate confidence, with deepest colors the most confident and white no confidence at all.
The hues would run from reddish blue to blue, teal, green, yellow, organge, and red to bluish red, with a little gap between the two ends to avoid confusion. Neutral would be either yellow (a happy, central color), or green (a nice, “green” color).
Measuring R G and B on a scale of 0 to 1, Depth D would equal (3-R-G-B)/2, so that pure white (R = G = B = 1) would give D = 0, and pure R G or B, D = 1. Colors like cyan (B = G = 1) are in fact brighter than pure B or G, so this formula would give them D = .5, while teal (B = G = .5) would give D = 1. (The conventional “Luminosity” measure treats cyan the same as B or G, which isn’t right.) As Depth declines from D = 1 to D = 0 by adding the missing colors, saturation would be held at 100% while the hue would be held constant.
I’d suggest using perhaps 11 hue brackets to indicate temperature, in order to give topo-lines of temperature as in the present NASA maps, but continuous shades of D. A region that was hot for sure would be red or bluish red, while one that merely probably hot, based on distant extrapolation, would be pink, fading into white as ignorance became complete. A region that was cold for sure would be blue or reddish blue, while one that was merely probably cold would be light blue, also fading into white.
I have created another version of the Lambert Equal-Area Projection. I call it an Arbitrary Axis LEAP. This particular one shows the poles rotated 90 degrees so that they are on the least distance distorted portion of the LEAP. Any point on a sphere can be rotated in this way to present it with less distance distortion.
I think it would show STAs near the poles with the least distortion of all the rectangular maps. It is an instance of the more general form.
Sorry my image wasn’t included. Try here.
Re #126, 127, Esnips link doesn’t work without an account. If you e-mail it to me (mcculloch DOT 2 AT osu DOT edu), I can upload it and post it.
Here is the image John Bell tried to display in #126, 126:
John writes,
Re John Bell’s Arbitrary Axis Lambert Cylindrical EA projection in #129, the one advantage of a rectangular projection (Equal Area or not) is being able to visualize latitude and longitude easily. So I’m afraid this version of the Lambert CEA defeats the whole purpose.
If you want both poles in the same graph, the complete Lambert Azimuthal EA, with an Equatorial viewpoint as in #43 above does that with less distortion of the continents. As in the Werner/Cordiform and Bonne projections (#61-69), a little clockwise rotation, to about the longitude of Switzerland (10 deg E) would bring Australia into the picture better and make the landmass better surrounded by ocean.
Or, if you want less distortion at the poles and don’t mind splitting the map, two half Lambert AZ EAs, with polar viewpoints as mentioned in #118, would be less disorienting.
Yet another great Lambert EA projection that is worth taking a look at is his Conic EA, one of the many options on Vaz de Almeida et al’s Map Projections website, the great Java application John mentions in #129. This is like the Lambert Polar AZ EA, except that it has been split half way through at the pole, and then the lines of latitude shrunken until there is no distortion at a selected reference latitude. The result looks like a pizza with a big slice removed. It is conic since the lines of longitude are straight lines emanating from the pole with equal angles between them, but the lines of latitude are spaced unequally so as to keep areas equal.
Speaking of interesting projections, one really big drawback of Buckminster Fuller’s Dymaxion projection in #111, 119 is that it sprawls all over the page, so that it must be greatly reduced in order to fit. You get more detail per dead tree with Mollweide or Lambert Az EA, and actually get even more with the Bell-Lambert Isometric CEA, since it fills its entire 2:1 box.
Re: 41, 111, 119:
One of the reasons I like the Fuller projection is – that I can build one! I am thinking of a 5/8 2v 30ft diameter geodesic dome (2″ aluminum struts: 9.27 and 8.197 ft length struts).
By placing a projector at the center of the inscribed sphere, one could use google earth maps to generate properly scaled gnomonic projections.
Why I like this: if I gave each audience member a USA dime, and projected on the map a section showing Lake Tahoe, California, I could mention that the dime, at the same scale as the 30 foot diameter globe, represents the volume of Lake Tahoe (although the dime’s thickness would be 7 times the actual)and that this represents all of the world petroleum crude lifted from wells and refined into gasoline, diesel, jet fuel, asphalt, etc from 1960 to 2007. The same from 1865 to 1960 would add 20% (1/6th the thickness of the dime instead of 1/7th being conservative.)
Bottom Line: if you also have access to Faraday’s excellent lecture “The Chemical History of the Candle”, you would know that the process of burning – Carbon and Oxygen yielding CO2 and energy, is the same as breathing. 15% or 20% of the CO2 being generated every year is not from automobiles and power plants but from humans and cattle and sheep and lions and buffalo and birds breathing!
Anyways, not to go off-topic, but to add again the pro’s of a Fuller (Dymaxion) projection map.
Re #125, 124, the temperature scale Steve used in #44 is close to what I had in mind for representing temperature with 100% certainty, since it runs through the spectrum without including white as does the NASA scale in #109, 123. White can then represent 0% certainty, with intermediate shades representing fractional certainty.
My primary reservation with Steve’s scale that it uses pale green, pale blue, cyan, and light yellow, instead of deep shades throughout. On a scale of 0 to 1, G = 1 and R = 1 are good deep colors. B = 1 as I suggested in #125 is perhaps too dark, and could be subjectively lightened a little to something like B = 1, G = R = .2. Pure yellow (G = R = 1) is too light, but cutting this in half, as I had suggested in #125, gives a murky olive color. Still, it could stand to be darkened to a rich egg yolk color, say to G = R = .95. Cyan can darkened substantially, say to B = G = .75.
#132. I used a symmetrical coloring scheme here, but the positives were stronger than the negatives – hence stronger colors. The fields package has a coloring scheme called tim.colors that has a range from red to dark blue that works very well IMO. If positive and negative are asymmetric, I manually set the breakpoints so that the max negative equals the max positive so that the deepness of the hues match.
Lonnie Thompson et al. introduce a Pseudo-Mollweide projection in their article in Climatic Change 2003:
This looks like a Mollweide at first glance, since it has an elliptical outline and horizontal lines of latitude. However, the latitudes are equally spaced as in the primitive NASA Equirectangular projection, rather than subtly adjusted so as to keep areas equal as in the 1805 true Mollweide projection. As a result, Antarctica and the Arctic Ocean are much too big.
The following true Mollweide image (by “Mfd” on wikipedia) shows the lines of latitude and longitude better than the copy I originally posted above:
Ironically, one purpose of the Thompson et al. map was to illustrate how important the tropics (and their temperature) are for humanity. However, the projection they invented actually underrepresents this region areawise! (Though not by as much as the Hansen/NASA Equirectangular, admittedly.)
The recent discussion of March 2008 Radiosonde data, at http://www.climateaudit.org/?p=3161 shows the following graph of atmospheric temperature by height versus latitude, taken from RealClimate at http://www.realclimate.org/index.php/archives/2007/12/tropical-troposphere-trends/, and originally probably from NASA/GISS:
Because Latitude is given in a linear degree scale, this graph exaggerates the importance of the poles, much as the equirectangular projection does. In order to eliminate this distortion, it is necessary to plot sin(latitude) rather than latitude itself on the horizontal axis. This is the same sin(latitude) that appears in the Lambert Equal Area Cylindrical projection.
With this transform, on a scale of 0 to 1 from the equator to N Pole, 30deg N would be at 0.5, 45 deg N would be at 0.71, and 60 deg. N would be at 0.87, rather than at .33, .50 and .67, resp, as in the existing plot The dark red high-altitude hot spot above 75 deg. N would still be present, but would be much smaller than depicted. On the other hand, the mid-altitude tropical hot spot would be somewhat larger than depicted.
It is most unfortunate that NASA still has not caught up with this vintage 1772 technology.
Re # 135 Hu
Agreed. Should use sine on X axis for a start.
(Some approximate statements follow). Another problem is that as you move from centre to edges, the incident angle of the sun changes; so does the length of atmosphere through which sunlight travels at a given altitude. Downward light radiation has to be plotted in a horizontal direction at the margins.
The data at the Equator are taken from above the whole Earth circumference. The data at – 90 and + 90 deg are taken above a single point, so sampling density is not constant.
Conclusion: It’s really a cartoon, not a map.
? Solution: The rotating spheroid, Google Map style, has advantages.
Some may find this interesting.
THE MYSTERIES OF THE PIRI REIS MAP ©by Diego Cuoghi
Part 1 (Piri Reis) – Part 2 (Oronce Fine) – Part 3 (Philippe Buache) – Parte 4 (Atlantide, only in Italian)
http://xoomer.alice.it/dicuoghi/Piri_Reis/PiriReis_eng.htm
Re Sam Urbinto, #137,
Piri Reis is way off-thread, off-blog, and, some would argue, even off-web. However, part 3 of Cuoghi’s site presents this unique 1531 double cordiform equal-area map by Oronteus Finaeus:
Fine’s data is admittedly a little sketchy — certain Canadians in the audience might object to his splicing Newfoundland onto Siberia. However, the projection itself is quite sophisticated. He has terminated the Stab-Werner N. Polar cordiform projection (#61-63, 67-68 above) at the equator, and spliced on a S. Polar cordiform projection, also terminated at the equator.
The resulting double cordiform polar projection puts GISS, and therefore NASA, to shame (cp. their abysmally primitive double ortographic polar projection, #109, 110, 123 above).
[snip ..sorry]
Re #138, here’s another try at the 1530 double-cordiform map of Oronteus Finaeus:
The URL is http://xoomer.alice.it/dicuoghi/Piri_Reis/Finaeus.jpg“
Re # 135 Hu McCulloch
The following news release just made by the US Geological Service might, in the meantime, be of some help in presenting mapping. It’s free and one can ask for different projections.
Click to access USGS_Landsat_Imagery_Release.pdf
Geoff.
Hu #138 “Piri Reis is way off-thread, off-blog, and, some would argue, even off-web. However, part 3 of Cuoghi’s site presents this unique 1531 double cordiform equal-area map by Oronteus Finaeus”
The point of posting that was threefold. And map focused, rather than on crazy conspiracy theories! 🙂 It’s really rather all very scientific.
First, with all the talk about maps, I thought it would be interesting to see how myths and legends of the mysterious land of Australia back then got moved, twisted, and put into interesting shapes (especially given my interest in Tierra Del Fuego /Cape Horn, Drake Passage and Antarctica and how close South America is to Antarctica.
Second, it’s interesting to see how doing the best you can to show the real world sometimes presents information that’s not quite right, but is the best you have; which others may misinterpret and present as clearer than they are.
Third, it’s got a lot of cool maps and map styles on it.
Now if only somebody that spoke Italian would translate that fourth page. 😀
Then again, thinking of the scientific method, amazing how they could get so close back then given the speed at which communications went, and 1/7th the number of people alive. Ha! Consensus, yes.
[snip]
The Wikipedia article on Global Warming now features Mollweide maps of global temperature anomalies prepared by Robert Rohde from NASA-GISS data. Here is an example:
Wikipedia has now left NASA in the dust, as far as mapping technology goes!
CRe: Hu McCulloch (#143),
Comparing a warmer 9 year period to one of the colder 40 year periods certainly helps to generate a map with a positive anomoly. Makes you wonder what periods could be selected in a future New Maunder Minimum dominated climate to generate maps with continued positive anomolies?
You all seem to be very well informed and all seem to have an abundance of images.
Could anyone help me as I am trying to teach projection at a very basic level, I felt the best way was to have different cut outs of projections of North America which students could compare and simply realise that they are different BUT I cannot find main projections of the USA that are simply oulines I can cut around, just to get an idea of the basic subtle distortions. Can anyone help provide me with these. Id love a Mercator and Robinson projection and an example of a conic and planar projection of at all possible, thank you.
RE Gemma, #145,
If you want to illustrate mapping distortions, N. Am. will show them a lot more clearly than just the USA.
I don’t know where to find the specific maps you request — I just got MATLAB’s mapping package, which should make it easy, but I haven’t figured it out yet. Perhaps you can google “Conic Projection North America” etc and find what you need. The maps will have details, but you can just transfer them to plain paper or posterboard.
IIRC, even Excel has a mapping option you can install…