Last year, Ross McKitrick proposed the ironic idea of a “T3 Tax” in which carbon tax levels were related to observed temperature increases in the tropical troposphere. Temperature increases in the tropical troposphere are, as I understand it, a distinctive “fingerprint” for carbon dioxide forcing. Apparent discrepancies between a lack of warming in satellite data and surface warming have been a battleground issue for many years. In one of the most recent surveys of the matter in 2006, the U.S. CCSP proclaimed that the issue had been put to rest:
Previously reported discrepancies between the amount of warming near the surface and higher in the atmosphere have been used to challenge the reliability of climate models and the reality of human induced global warming. Specifically, surface data showed substantial global-average warming, while early versions of satellite and radiosonde data showed little or no warming above the surface. This significant discrepancy no longer exists because errors in the satellite and radiosonde data have been identified and corrected. New data sets have also been developed that do not show such discrepancies.
In this respect, the March 2008 satellite data for the tropics is pretty interesting. The graph below shows UAH (black) and RSS (red) for the tropics (both divided by 1.2 to synchronize to the surface variations – an adjustment factor that John Christy said to use in an email). I also collated the most recent CRU gridded data and calculated a tropical average for 20S to 20N, shown in green. All series have been centered on a common interval.

Figure 1. Tropic (20S-20N) temperatures in [anomaly] deg C. All data shown to March 2008. Script for calculations is given in #19 below. Reference periods for original data converted to reference period 1979-1997 here.
There have only been a few months in the past 30 years which have been as cold in the tropical troposphere as March 2008 four months in the 1988-1989 La Nina. At present, there is no statistically significant trend for the MSU version. The data set has very high autocorrelation (but I note that autocorrelation doesn’t represent the spikes very well.)
Obviously each fluctuation is unique – I presume that we’ll see some sort of behavior in the next 18 months like after the 1988-1989 Nina – so that one can reasonably project that the long-term “trend” as at the end of 2009 will be a titch lower than the trend as calculated today.
While RSS and UAH move together, there is a slight drift upwards in RSS relative to UAH and there’s still a slight trend in the RSS numbers. There’s a third data set (Vinnikov – Maryland) which is not kept up to date, which has trends higher than either. Even CRU is now reporting tropical temperatures at surface that are below average during this period.
I draw no conclusions from this other than some claims about the statistical significance of trends need to be examined. The autocorrelation of the data set is very high; although I’m not in a position to pronounce on the matter, the concerns expressed by Cohn and Lins about long-term persistence seem highly pertinent to the sort of patterns that one sees here. Some readers may note a graphic in summer 2005 .
realclimate discusses the issue up to Dec 2007 here. Since then, cooling has been 0.3-0.4 deg C in UAH and MSU.
UPDATE: This post has occasioned references to Douglass et al 2007. Here is Table IIa from that paper.





475 Comments
How does _delta_ T look? Especially for trends longer than three months? IOW, visually I only see a couple sustained-dropping-temperature spots. 1) Are those spots real and 2) what are the non-visually-apparent next-steepest?
The projected greenhouse warming pattern is indicated by this IPCC plot . As can be seen, the tropical upper troposphere should show a distinct temperature fingerprint from AGW later this century.
Another way to check for the beginnings of the fingerprint, besides surface vs lower troposphere, is to look at tropical lower troposphere vs mid-to-upper troposphere. This is available from satellite data and is shown here , including the weighting function. (Note that Ross’ T3, the purple line, has stratospheric “contamination” and so, while the principle is intect, some other measure of the T3 fingerprint is probably needed.)
This plot, like Steve M’s plot, fails to show evidence of the AGW fingerprint. Perhaps 2008 is too early, but I’d expect to see at least a hint by now.
Concerning recent months, the temperature of the tropical upper troposphere ( see this Hovmoeller plot ) continues to show anomalously cool readings. If water vapor in the tropical upper troposphere is a function of temperature then there’s currently less water vapor there to slow IR loss, so Earth is bleeding extra IR into space at the moment.
Concerning the trends, I sometimes wonder if, in recent decades, the tropics have been moving an increased amount of their heat poleward for removal there, rather than doing the removal in the tropics.
Strange how these corrected mistakes favor AGW 99% of the time. (It’s probably 100% but I’m trying to be conservative here)
If you want to know what the fingerprint should look like, the most recent (controversial, disputed by RC) paper on the subject (your probably already aware of it) is here:
Click to access DOUGLASPAPER.pdf
I suspect that the RC critique (shouldn’t be too hard to find) is an attempt to obfuscate about taking “errors” into account that would make any denier flush red in the face.
The abstract to the paper linked in #5:
Tropical “hot spot” in the middle troposphere at 8-12 km is unique greenhouse warming signature, but is is entirely absent from both satellite and weatherballoon data. Warming rate which should be 2,5 -3 times faster in the troposphere is actually smaller than at the surface.
US CCSP so called overcoming of discrepancies between surface and atmospheric measurements concerns only global averages. But in the same report Steve cited it is clearly indicated that in the tropics discrepancy remains unresolved, because trend is larger at the surface than in the atmosphere. Report only speculates, in the good climate science tradition, that maybe data are wrong, not models. For analysis of that discrepancy and explanation of complete absence of greenhouse warming signature in tropics see Douglas et l 2007.
oops, my comment is redundant. I started writing it before comments 4-6 were posted, so you can ignore my reference on Douglas paper, since it was linked and commented in the meantime.
Steve,
I must say that I’m not particularly astonished that RC should have had no comment on this “pernicious” issue since Dec 2007. The global downward anomaly for the period 01/2007 through 01/2008 was approx. -0.7C [as noted by Anthony Watts and several others, the single largest temperature drop on record anywhere].
I know that 15 months certainly does not even begin to make a trend, but another 0.3C slide in tropical troposhpere temperatures since then certainly must be confounding to some.
Re 3
Thats because if the results match what they expect then they accept them and dont look for errors, whereas if they dont match then they are investigated until they find an error.
Even when looking for an error they will only look in one direction. For example with the TT temps, because they expected the temps to be higher the question they would ask themselves would be be “What could possibly make the temp readings lower then expected?”. That is the only type of error they would look for.
RE#4 Andrew
IIRC, Tamino simply inflated the error boundaries, viola! Problem solved.
In my unscientific mind it is a concern that the most modern temperature measuring devices we have (satellite MSU) have now been corrected to correspond to the most corrected set of measurements in history. The data from the HCN maintained by NASA GISS. It makes one wonder why? Perhaps there is a mouse in the works. I wonder if there will have to be new corrections when the new CRN comes online later this year? I Also wonder what the results will be when the other 1000 weather stations are overhauled will be. I can foresee some true surprises for the climate study community.
Just my 2 cents,
Bill Derryberry
Hey Steve,
Where did you get this data from? How close do the raw data look (that is without the modifications you did to plot them up together)?
Also, do you think you could add another plot of the data you have plus the Nino 3.4 index?
thanks
Re year 2008 RC comments on Douglass et al
See
Start at Ray Ladbury 120.
Re introductory graph
I had previously thought that there was a time lag between upper troposphere temperatuures and surface temperatures, especially since surface sea temperatures were supposed to have an appreciable inertia. So I’m surprised that there is such good correspondence on the time axis, in a coarse sense.
Second, with three measurements marching in lockstep, what is the dominant common cause? Is it still said to be CO2? Or is it Noel Coward’s Mutual Admiration Society?
Andrew #4 The criticism of the Douglass et al. paper on RealClimate was spot on. They incorrectly used the standard error of the mean instead of the standard deviation to measure the spread of the models, which is quite obviously wrong. This made the error bars about four times narrower than they should have been. Re-running the analysis with the correct statistic shows the observations are consistent with the models (i.e. the opposite of their conclusions). There were other issues, but this particular point is not contraversial at all, Douglass et al. got it completely wrong.
I don’t see why short term events such as this are at all interesting in a discussion of climate. Aren’t they just variations due to ENSO? It would be interesting to plot a rescaled NOAA ocean nino index (ONI) along side.
#15
In other words, they demonstrated that there is so much variation in the model’s outputs that even a complete absence of tropospheric heating cannot be said to be inconsistent with AGW.
#15 and 16,
So we have a high level of confidence that the power of the test stinks. What then is the point of the exercise?
re 17, yes the signal is small the error in the models is large, so you have to
wait thirty years to render a judgement, but until that time is up any attempt
at falsification is unsound, and you should just accept the models because.
but hey
Judd, here are scripts for locating and downloading the tropical temperatures. CRU does not publish a tropical average, so in this case I downloaded their gridded data (about 40 MB unzipped) and extracted a tropical average from it. The extraction of a tropical average show R and ncdf at their best. The nc file can be uploaded into R from the Hadley Center without having to do any manual copy operations; after that, a couple of matrix rearrangements – which R does magnificently.
#MSU
url=”http://vortex.nsstc.uah.edu/data/msu/t2lt/uahncdc.lt”
fred=readLines(url);N=length(fred)
msu=read.table(url,header=TRUE,nrow= N-4)
msu=ts(msu,start=c(1978,12),freq=12)
msu.trp=msu[,”Trpcs”]
#RSS
url=”http://www.remss.com/pub/msu/monthly_time_series/RSS_Monthly_MSU_AMSU_Channel_TLT_Anomalies_Land_and_Ocean_v03_1.txt”
tlt3=read.table(url, skip=3)
dimnames(tlt3)[[2]]=c(“year”,”month”,”70.80″,”20.20″,”20.80N”,”20.70S”,”60.80N”,”60.70S”,”US”,”NH”,”SH”)
tlt3=ts(tlt3,start=c(1979,1),freq=12)
tlt3.trp=tlt3[,”20.20″]
#CRU
library(ncdf)
download.file(“http://hadobs.metoffice.com/hadcrut3/data/HadCRUT3.nc”,”temp.dat”,mode=”wb”)
v< -open.ncdf("temp.dat")
instr =1979)&(time(monthly)<1998) #common center on 1979-1997
tsp0=tsp(monthly)
monthly=scale(monthly,center=apply(monthly[temp,],2,mean),scale=FALSE)
tsp(monthly)=tsp0
monthly[,1:2]=monthly[,1:2]/1.2 #divide troposphereic by 1.2 per John Christy advice
ts.plot(monthly,col=1:3,xlim=c(1980,2009),ylim=c(-.8,1.3))
Re #12 Here’s a plot of RSS Tropical LT Anomaly and ONI, with a few notes:
#15. I’m doing chores today but will do an ENSO plot. I’m sure that the gross fluctuations will correlate highly with ENSO, but I think that the principal interest from these plots is a little different than the traditional dispute. Let’s suppose that ENSO has 1/f autocorrelation and this is hardly an unreasonable hypothesis – one can even think of physical reasons. Indeed, I’m surprised that this hypothesis doesn’t seem to have been studied exhaustively. If you can get downspikes from an individual Nina and upspikes from an individual Nino of the order that has been observed, then you can get readily get unforced decadal fluctuations consistent with the observed history of the past 30 years. This doesn’t prove that there was no forcing – since the history is also consistent with a slight trend plus 1/f fluctuations. Just that the “significance” of any trends becomes less clear as you get allow for more autocorrelation. And ENSO is not an external forcing, but part of the climate system. So if you have highly autocorrelated ENSO with persistence, then that’s the sort of noise that you have to allow for in trend significance testing. Which puts IPCC in the wrong in their handling of Cohn and Lins.
#20. David and others, as I understand it, “ENSO” is now defined as the temperature of a sector of the PAcific Ocean. So at one level, one expects the temperature of the PAcific – the most important system on earth and especially in the Tropics – to be correlated to the tropical temperature.
But for #15 and others, if ENSO is defined as ocean temperature in a Pacific sector, it doesn’t explain tropical temperature. It is a component of tropical temperature.
#20, David,
Can you see the step change more clearly if you plot the difference between the two? That they’re correlated is no big surprise, but that step has always interested me. Is there anything besides the coincidence of timing to connect it to the AMO?
Sorry if that’s off topic, but it’s been bugging me for a while. Is there any way to tell statistically if a step function gives a genuinely better fit than a linear function?
Regarding the upper troposphere hot spot, the impression I had got was that it was an indication of lapse rate feedback, which supposedly occurs in step with (but with opposite sign to) the water vapour feedback that amplifies warming. That would mean it is not so much a fingerprint of greenhouse warming so much as general amplification of surface warming from any source. Does anyone know if that’s true?
Re #22 Agreed.
Interestingly, the ONI region (5N-5S;120W-170W) covers only 3.6% of the tropics (20N-20S) yet plays a major role in tropical temperature variation. I believe that’s because it straddles a critical temperature for placing heat into the atmosphere (when it warms, it creates considerably more thunderstorms).
The interesting things in the plots are the apparent effects of the volcanoes and, more importantly, the upward move in temperature when the Atlantic warmed in the 1990s/early 2000s. An alternate plot is here .
22 (Steve)
Nice distinction. Lets forget about ENSO and ask another question entirely. It’s this one:
Is the Tropical LT anomaly that relates to the entire globe (that David Smith shows in #20) due to an ‘internal oscillation’ or is it externally forced?
Where can the tropics (mostly ocean) acquire all this extra warmth and what is the mechanism that causes the swing between acquisition of warmth and that which we are currently experiencing, a solar minimum chill?
If the swing in temperatures around the whole globe is not the result of an interaction between the sun and the Earth’s atmosphere I will eat three hats of your choosing as long as they are made of ice cream. If you can demonstrate that it is due to another mechanism entirely I will eat six hats.
Re: #15
Beaker, that’s my reading on the critique of the Christy paper. What that critque is saying is that “on average” the climate models show the middle troposphere warming more than the lower troposphere in the tropics while the statellite measurements show the middle tropospere warming slower than the lower troposphere, but that the climate models have so much uncertainty associated with them that one cannot conclude with X probablity that results of the models and measurements are different. We discover just how much uncertainty these models have (and from the supporters of them) when these seeming contradictions arise, e.g. the crtiques of the climate models used in the recent Emanuel et al. (2008) paper on the relationship of SSTs and TC activities.
By the way, Beaker, perhaps you could post the probability of the climate model and instrumental results being different along with the corrected standard deviations for the model output and instrumental measurements. That is really what this whole issue boils down to.
I forgot to add how all this uncertainty could effect the Ross McKitrick T3 tax on CO2 emissions. I guess we would delay the imposition of it until such time as we could determine that the model uncertainties were sufficiently small to determine what the satellite results were telling us about CO2 related global warming. I could live with that.
15 (beaker): Well you’ll have to forgive me for never believing anything that comes from them. Okay, so, if the descrepancy is all down to problems with the observational data, what are the problems? What needs to be done to “fix” the data? If you can’t come up with a reason “you don’t even have anything worth denying”.
The CCSP 1.1 was finalized in late 2005 and did not include (though I gave it a try) the information that was either “in press” or close. So, the CCSP is out of date. In Christy and Norris (JTech) 2006 we determined that UAH data were more highly consistent with VIZ radiosondes than RSS and that UAH data were more self-consistent than RSS in a detailed analysis.
In Christy et al. 2007 JGR we specifically dealt with every tropical radiosonde along with UAH and RSS temps. Again, the UAH data were more consistent with all other datasets and the results specifically pointed to a likely spurious warming shift in RSS data in the early 1990s (RSS is the only dataset which shows significantly warmer tropical tropospheric temperatures in the three years AFTER Mt. Pinatubo – the surface didn’t even show that.)
Finally, Randall and Herman (JGR 2008) used a window technique to independently identify a likely spurious warming shift in RSS data in the early 1990s.
The key thing about Douglass et al. is that we specifically designed the experiment as a hypothesis test – meaning we needed model surface trends which matched the observed surface trend so we could compare upper air temperatures in an apples to apples comparison with observations. Many critics (i.e. RC) seem to have failed to grasp this conditional requirement. In other words we asked a very simple question, “If models had the same tropical SURFACE trend as is observed, then how would the UPPER AIR model trends compare with observations?” As it turned out, models show a very robust, repeatable temperature profile … that is significantly different from observations.
What I’ve found almost humorous is trying to be scientific about all of this. If rapid human induced warming is claimed as a hypothesis (in models) then how can it be stated in such a way as allowing for the possibility of it being falsified? The possibility of falsification is required for any hypothesis. However, as soon as we construct a test, (i.e. comparing upper air tropical temperatures, where the clearest GHG signal occurs, with observations) many cry fowl and object. How do you create a test to check the falsification possibility for assertions (hypotheses) of rapid, GHG-induced warming? If there is no possible falsification test, there is no science. As my colleague Roy Spencer likes to say, “No one has falsified the hypothesis that the observed temperatures changes are a consequence of natural variability.” (Let me add that I think there should be some warming due to the enhanced radiative forcing – just not catastrophic.)
John C.
BTW, I’m not sure how closely related it will be to that paper, but I have heard from a reliable source that Douglass is wroking on a similar paper. Should be interesting. Also, I would like to comment that RC really should have had their critique published rather than just blogging about it. What kind of science is that?
#21, Steve, your logic and intuition about the autocorrelation nature of ENSO is accurate. ENSO is phase locked to the seasonal cycle, hence the ability to predict January ENSO indices with July SSTs. However, the April persistence barrier precludes the converse prediction. A pretty good prediction for 2008 would be the continuation of La Nina conditions in the central and eastern Pacific.
Some of this “match” may be the scientists desire to prove that everybody is stating the same thing (consensus). With this data, would we EXPECT to see such close fit, or has the data been forced to fit? There still appears to be some “divergence” at times, they should be looking at these points. THAT’s where the signal is probably hidden.
#20 & 24.
Thanks for the plots, David. Nino 3.4 and the RSS tropical LT temp co-vary, and the relationship appears very strong (did you compute the covariance?). However, the divergence between the two in the 1990’s/200’s is also interesting. In your post #24 you plot a pink line and label it as “Warming Atlanic”. In #20, you label it as (AMO?). How do you distinguish between the AMO and a trend? Do you have a timeseries of the AMO by any chance to see if this time period correlates with a swing in the AMO?
John Christy, thanks as always for your contribution.
Over at UnrealClimate, gavin excoriatiates you roundly for allegedly using an older version of RAOBCORE. I had a couple of questions:
First, what is the real story about the use of V1.2 of the RAOBCORE data instead of the 1.4 version?
Second, the RAOBCORE dataset is a reanalysis of the balloon data. This means that the balloon data is reprocessed using a climate model. The input data for that climate model, in turn, comes from the NCAR/NCEP Reanalysis of global temperature. This temperature reanalysis, of course, is also based on a (different) climate model. So the RAOBCORE dataset is data which has been “reanalyzed” by tweaking it based on not one, but two climate models.
Seems to me the RAOBCORE results (particularly V1.4) have been hopelessly polluted by the climate models. My question is, after being “reanalyzed” by comparing them to two climate models, shouldn’t you be considering the RAOBCORE reanalyzed dataset as model results? Or at least as some kind of hybrid, neither fish nor fowl?
My best to you,
w.
#29 JC
Your efforts to be scientific are greatly appreciated. Regards
00.13 on 28 April and I’ve just downloaded the MSU file, using the address supplied by Steve in his R script. As a first try I’ve looked at the “Globe” column – the third in the array of 28 columns, as perhaps being most typical of them all. Of course, the “Trend” quoted in the file is exactly what I find (0.137). Looking at other details of the “trend” it is very highly significant indeed, and there, I suppose, many would consider the matter closed.
HOWEVER, for those of you with the means to examine the data using regression software what I advise is separating it into two blocks, to wit, before and after June 1997. Now examine the two separate segments. What you will find is is that the early set has a mean of -0.0324, a “trend” of 0.00304, (t = 1.505, prob 0.134). The later set, ending in March 2008 has a mean value 0.237, a slope of 0.00307, with t = .611, prob 0.54. The standard deviations of the original values are 0.162 and 0.177, so there’s no detectable difference in variance for those of you who are worried about that aspect of the analyses.
What happened is that around mid 1997 there was a /very/ rapid change of average of 0.27 units (degrees C ?). Prior to and after this step change date there were no enduring changes in “Globe” as reported by Uahncd.
I have run only one other analysis of the collection so far – it’s too late for me – and this also showed a step change.
How is this abrupt change demonstrated? By using industrial quality control methods, in particular by plotting the cusum of the whole series and noting that it divides very clearly indeed into two segments that are (on the grand scale) straight lines. These have a graphical estimate by me of slope difference (simple approximate geometry) of about 0.28. This rough eyeball estimate matches very well the one generated by using the least squares trend estimates.
The requirement for the data to be regarded in two segments is absolutely clear. Uahncd’s trend estimate (readily verifiable as I’ve noted) serves to hide the real structure of the data, which is of two effectively stable segments punctuated by a step change of nearly 0.3 units.
I can provide all the graphics as GIFs if anyone wishes it.
Step changes of this sort are very common indeed in climate data. Just look at the CET data available from the Hadley centre, for example. It is all very fascinating.
Robin
You may wish to refer to the CCSP Synthesis and Assessment Report on Tropospheric Temperature Trends, the executive summary is at http://www.climatescience.gov/Library/sap/sap1-1/finalreport/sap1-1-final-execsum.pdf. The information has about the same currency (date) as the IPCC, but provides more detailed explanations than the IPCC.
Here is why I don’t think the tropical tropospheric temperature trends is a good litmus test for AGW. The physics underlying the amplified tropical tropospheric warming in the models is the decreasing slope of the saturated adiabat as temperatures warm. Deep convection throughout the tropics will therefore result in saturated adiabat having a dominant influence on the vertical temperature profile, and hence result in the upper tropical troposphere warming faster than the surface. In climate models, it is the convective parameterization that determines this vertical transport of heat. The biggest achilles heel in climate models is probably the convective parameterization.
I have referred to this paper before on CA
Click to access Agudelo_GRL31.pdf
I would like to draw your attention to Tables 2 and 3, discussing tropospheric temperature trends in the ERA (European Reanalyses). The tropospheric trends in the ERA are arguably more accurate than those in a climate model, since the ERA is constructed from a weather model with data assimilation. This analysis highlights the complexity of regional variations in upper tropospheric trends associated with regional changes in atmospheric dynamics.
So the bottom line is that the canonical tropical upper troposphere fingerprint from simple radiative convective models and climate models depends on highly uncertain convective parameterizations. I would like to see a new assessment of the satellite-derived trends by people outside the RSS and Spencer-Christy groups. There are clearly new results of relevance since IPCC and CCSP, with both “sides” making different arguments and disagreeing. It will probably take some time to sort this out. But in the mean time, i personally wouldn’t put too much emphasis on this particular fingerprint.
Per the earlier comments on the relationship between tropical lower-troposphere temperature and tropical SST, a relevant plot is here .
It’s a close relationship, as expected.
There is another, controversial analysis (which I think Steve mentioned above) which apparently is not kept up to date. There is a rather old, and I suspect very out of date comparison of the three data sets here:

Which I think is missing some changes that have subsequently been made to the UAH data that bring it closer to RSS, but the graphic serves to illustrate that Vinnikov’s analysis is way above both (I’m sure the reason is mysterious). It would be nice if some one could point me towards the latest version of that analysis. Obviously, to me at least, that data will show more Tropical warming to.
Re: #38
There’s that word uncertainty used once again in the same sentence with climate models — and again not by a skeptic/denier.
Re: #36
Robinedwards, I have looked at change points on UAH temperature series for the globe and zonal areas of the globe on an annual and seasonal basis. I just went over my previous calcultions and determined that they required corrections. I plan to post all the corrected data and sources to change point analyses on the unthreaded thread tomorrow.
Judith, always good to hear from you. I fear, however, that your point is not clear.
The Douglass Christy et al. study, to me, showed that the models are deeply flawed in how they represent the tropospheric changes in the tropics.
It seems to me that you are saying that that result of the study is invalid because the models have “highly uncertain convective parameterizations”
But isn’t that what the study just showed? That whatever the parameterizations are the models are using, they’re not working?
What am I missing here?
w.
44 (George M): For a background on the data and corrections made to UAH’s data set over the years, you’ll want to read:
http://www.uah.edu/News/climatebackground.php
Re: RAOBCORE v1.4 and ERA. It has been shown by several studies the the ingestion of the HIRS 11 and 12 channels in ERA-40 led in 1991 to spurious (a) rise in 700 hPa specific humidity (.3 g/kg), (b) sudden increase in 200 hPa divergence (10-7/s) (c) sudden increase in tropical precipitation (0.5 mm/day) and other related variables. v1.4 of RAOBCORE depends strongly on ERA-40, so it also shows the same spurious shifts. We had looked at v1.4, but its unrealistic trend profile (and that of ERA-40) were highly and significantly different from in-situ measurements so we could not justify its use. ERA-40 has some other problems, for example a spurious warming of the MSU on NOAA-10 when there is no evidence for that at all.
The upper tropical troposphere/lower stratosphere in ERA-40 has no parallel with in-situ observations. But, to balance the outgoing IR in the reanalysis product, the lower troposphere in ERA-40 actually shows cooler trends than expected in the tropics with a surface trend for 1979-2004 of something like +0.02 C/decade (I don’t have the CCSP chart with me). So, the evidence indicates the upper troposphere is warming too much, and the surface not enough in ERA-40.
The study of Randall and Herman was done independently of both RSS and UAH.
It may well be that the tropical fingerprint we identified is a poor hypothesis test in terms of the real world. However, it is a dominate and repeatable feature of all climate model simulations caused by their enhanced greenhouse forcing, so that is the test we could perform. One conclusion would be that models haven’t captured the proper greenhouse signal in their physics.
John C.
Willis, I am not disagreeing that the models are flawed, but i don’t think that that stating the models are flawed based upon comparison with potentially flawed observations is very convincing. The arguments for concern about the model convective parameterizations are based upon model sensitivity to different parameterization schemes, the inability to correctly simulate moist convection in complex mesoscale systems using more detailed process models , as well as on broad brush comparison with observations (detailed verification of the parameterizations is very difficult owing to the scales of variability).
Judith, many thanks for your answer. You say we can’t tell if the models are flawed “based on comparison with potentially flawed observations” … potentially flawed? Each and every observation ever taken is “potentially flawed”, so I’m not clear what you mean.
All of the models show increased warming trends starting just above the surface and increasing upwards.
All of the data shows decreased warming trends starting just above the surface and decreasing upwards.
Could you explain, in a bit more detail, exactly how the data is “potentially flawed”, and why you think that “potential flaw” negates the conclusions of Douglass et al.? I mean, RSS and MSU and balloons are all getting a very similar answer. Are they all suffering from the same “potential flaw”? And if so, what is it?
Seems to me that until the “potentially flawed” becomes “demonstrably flawed”, the Douglass data is just like every other piece of data on the planet — potentially flawed, but used nonetheless until someone can expose a flaw.
w.
Re #44
Based on scientific principles yes, but the corrections were necessary to take account changes in orbits, matching the orbital data of the succession of satellites used (RSS has used at least 10 satellites: versions), varying calibration of the on-board sensors and drift, and accounting for the vertical weighting functions of the various channels:
weighting fns
The derivation of temperature profiles from the microwave sounder data is very complex and S & C original work was a great achievement, however like many such advances there were many improvements necessary, hopefully it’s getting close.
As a very simplified comparison consider a thermocouple made of Platinum and a platinum/rhodium alloy. If you stick this in a flame you’ll measure a temperature which is inaccurate by ~100ºK, the reasons are as follows:
heating due to catalysis on the surface, cooling by conduction, convection and radiation which can all be corrected for or minimized in various ways, a lot of the work on this was done by NASA (when it was still NACA). Not as simple as it first appears.
38 Judith Curry
But this is a very serious flaw, putting pretty much all the results of the models in doubt. Natural convection is a process which short-circuits the GHG effect, by providing a parallel path for vertical thermal-energy transport.
In other words, the ‘blocking’ effect of CO2 is diminished in the lower part of the troposphere by the fact that natural convection provides a path around the ‘barrier’. A good analogy in electrical circuitry is placing a second resistor in parallel to the original resistor which was controlling current.
Pat, I agree with you completely. The tropics are the hot end of the planetary climate heat engine. If the models don’t get that part right, their results are … well, in my youth I would have said “not worth a bucket of warm spit”, but I’m a reformed cowboy now, so I’ll just say their results are not very believable.
In particular, a huge percentage of the vertical heat transport in the tropics occurs in the center of the thunderstorm towers. There, it is hidden from and does not interact with the middle troposphere at all (neither through convection, conduction, or radiation). Instead, the air is picked up from the surface, the moisture is stripped out of the ascending air column, and the dry air comes out at the very top, ready to descend and start the process over again.
This leads to a host of problems in the model representation of these events. One is that the throughput of the system (how much energy is moved) is not connected to the gridcell average values. Because the movement is a very localized phenomenon, the amount of heat moved can vary widely with very little change in average temperature or average humidity. Trying to tell how fast the heat is moving through the tropical atmosphere by watching the surface temperature is like trying to tell how fast your car is going by looking at the engine temperature gauge … doesn’t work very well.
A related problem is that the wet air is concentrated inside the thunderstorms, while the dry air is descending outside the thunderstorms. This can lead to a paradoxical situation where on average (since there are no hygrometers inside the thunderstorm towers) the air is measured as being less humid as the heat transfer increases …
w.
Robinedwards:
I had noticed the same thing regarding the RSS and UAH data in January. It seemed to me, just eyeballing the data and doing some crude Excel stuff, that what you said about data could be noticed in all the regional data. Not being much of a scientist (a rather lackluster BSc in Chemistry way back in ancient times), and lacking any statistical skills whatsoever, I contacted Wm Briggs and asked him about it. You might be interested in his response http://wmbriggs.com/blog/?s=RSS&searchbutton=Go%21.
Anyway, have fun trying to convince the people here. This is a very talented bunch and its a great place to drop in on – but I think sometimes they miss the forest for the trees. I’m writing this just to let you know there is someone out in blog land that thinks you have a very interesting observation and had the cahonies to write it up here at CA. I chickened out!!
Have to see what Kenneth Fritsch says.
I read this blog about 3 or 4 times a week. Have lots of simulation/math modeling experience but relatively little, almost no, climate physics experience. So given all that, I am confounded by the audacity of statements like that. Maybe the utterer doesn’t realize it seems like pandering in the extreme. Makes me think there is no test that will ever be approved for testing any number of AGW theoretical constructs. Could it be they are following the sacred gourd and don’t even know it or have convinced themselves otherwise?
The Briggs posting cited in #49 is worth reading. http://wmbriggs.com/blog/2008/02/09/how-to-look-at-the-rss-satellite-derived-temperature-data/
Re: 29
“If rapid human induced warming is claimed as a hypothesis (in models) then how can it be stated in such a way as allowing for the possibility of it being falsified? The possibility of falsification is required for any hypothesis. However, as soon as we construct a test, (i.e. comparing upper air tropical temperatures, where the clearest GHG signal occurs, with observations) many cry fowl and object. How do you create a test to check the falsification possibility for assertions (hypotheses) of rapid, GHG-induced warming? If there is no possible falsification test, there is no science.:
Can we start a best quotes of 2008? I nominate John C.
Isn’t science about tests? In light of the (less than) 2 degrees of separation between modeling teams conclusions, shouldn’t dissension, contention, and rebuttal be welcomed? It’s as close to our Hippocratic oath as we can get.
RE:53 Falsification – Gavin provides illumination on this issue.
From RC on Douglass et al, comments:
58. Terry Says: 14 December 2007 at 11:55 PM
So what you are saying is that the confidence intervals around the model predictions are so large that they are essentially unfalsifiable?
[Response: for this metric and taking into account the errors on the observations and shortness of the interval, yes. Different metrics, different time periods, different observations it’s a different story. – gavin]
All clear now?
Cliff
Re my # 14, lack of comment
My sensitivities being disturbed by silence, might I please expand briefly?
The satellite senses a mixture of events that are virtually immediate (reflection of sunlight) and delayed (heat emitted by a warmed land or sea, if you believe these have risen, following a path back to the region of satellite measurement.) The satellite is measuring gas temperatures some distance from solids.
The surface measurements are also a mixture, with comparatively less of the former and more of the latter. At any instant, the satellite is measuring a different entity to the thermometer on the ground, whose response probably has a time lapse from interactions with solid and liquid.
There are also often clouds between the two areas of measurement, but that’s been mentioned before, I recall.
So I can’t see why satellite temp should agree with surface, with no lag/lead, assuming constant solar irradiance, but I do not have a good feel for the magnitude of separation on the time axis that is appropriate (or could be modelled????)
BTW I have always thought that the ozone hole was on nervous ground because I have had to model multiple interactive simultaneous chemical reactions in physical systems. Coefficients derived from relatively pure mixtures at the start can go badly wobbly in real life. Looks like that’s what happened to ozone, if this paper stands scrutiny
http://www.nature.com/news/2007/070924/full/449382a.html
But this is OT since the hole never reached the tropical troposphere.
JChristy says:
If the hypothesis test had been performed correctly there could have been no major objection. Had the test been based on the standard deviation instead of the standard error of the mean, had it involved the error bars on the data, had the standatd deviation been computed directly over over the individual model runs instead of the means of the runs for each model, the objections would only be minor quibbles. As it is, the paper demonstrates (if imperfectly) that there is a statistically significant bias in the models, but not that the models are inconsistent with the data.
The claim Douglass et al. sets out to test is falsifiable, it is just that the test was performed incorrectly and it turns out the claim was not falsified by the test when conducted properly.
Steve, thanks for the comments regarding ENSO and autocorrelation. The point I mainly was trying to make is that if the spikes are due to “weather” related issues, such as ENSO, we would be better off not drawing attention to them as they will get used as evidence for or against some particularpoint of view on the climate when actually they don’t really tell you anything at all.
I do agree though that if you are going to perform significance tests, then you have to be very careful and make sure you get them right, and it is best to err on the side of caution. This is my major problem with the Douglass et al paper, it draws a strong conclusion that is not justified by the data because of clear errors in the statistical methodology.
Kenneth Fritsch says:
I can’t really do without knowing the uncertainty of the observational data, but as you can see from the plot from the paper, even the standard error of the mean of the observational data is not insignificant.
N.B. the error bars on the models should be about four times broader in order to represent the stadard deviation, and even this may be optimistic as the standard error was computed from the average for each model, which will also have reduced the apparent variance somewhat.
I think that the fact that real data fails to show the characteristic fingerprint of a CO2-induced warming is more important that alarmists would like to admit, because the fingerprint is not just something that “happens” as a result of the process. It’s what is NEEDED for the process to take place.
In the Green House Effect, the Earth’s surface warms because of some extra radiation it receives from the troposphere, due to the increased temperature of it (CO2 absorption of energy). This means that the models need that high temperature of the troposphere in order to show some warming of the surface. Warming of the surface would not happen without it. Now, if the surface temperatures predicted by the models are happening, but the warming of the troposphere is not, it automatically leads to the conclusion that there is another factor which is even more important than GHE and which is causing the warming of the surface.
And that is not all. Because if part of the warming of the surface is because of some different processes, those processes are also afecting the warming of the troposphere independently of the CO2 concentration, because the energy that the GH gasses absorb comes from the surface radiation which depends on surface temperature. This means that part of the only slightly increased temperature of the troposphere isn’t caused by the CO2 concentration, but by whatever other causes that are increasing the surface temperature.
If a model correctly predicts nowadays’ surface temperature increase, but wrongly predicts twice as large troposphere temperature increase, we can automatically say that the importance which that model gives to GH gasses concentration as a cause for the warming should be, at least, halved.
If there really are model runs that match the observations, which I guess there must be if the error bars overlap the observations, it suggests some pretty wild fluctuations in the models. It would be interesting to know if those model runs that specifically match the troposphere observations also produce catastrophic warming going forward.
If so, how do models with little tropospheric warming (in the past and present) produce catastrophic surface warming in the future?
Beaker, in 56 wrote:
But when the “claim” is defined as including all the uncertainty of the model’s outputs — which is what RealClimate has done to save the “claim” from Douglas et al. — then that “claim” is not longer consistent with AGW theory, as Nylo has explained in comment 59.
Interesting disconnect between beaker in 56 and Gavin in 54. So, who is right? Beaker claims that the claim is falsifiable, just fails to falsify, while Gavin claims that the claim is not falsifiable, so the paper was just a waste of time. Hmm….decide for yourself.
BTW, if I’m understanding correctly, John is saying that doing what RC says would essentially include situtations where the surface trends can mismatch, but if you make it a requirement at the outset that the surface trends match, then you cannot claim that the atmospheric trends match becuase the only situations where they would match are situations when the surface doesn’t line up. That’s my take from reading his comments in the UAH press release.
Andrew, thanks for the link in 63. Do I understand correctly, then, that what RealClimate did to save the “claim” from being contradicted by the troposphere data was to include model outputs that are contradicted by the surface data?
64 (Michael Smith): I have no comment on what RC did or did not do. I’m just summarizing what I think John’s point is.
What’s the cite for tropical tropospheric warming being a “fingerprint” for GHG warming? According to RC:
They give examples from ModelE.
Stratospheric cooling is a GHG specific fingerprint.
@66 Boris:
Whether the warming is from greenhouse gasses, El Nino’s or solar forcing, the stratosphere will warm, that is true. However, if the warming is induced by greenhouse gasses, that warming of the stratosphere should be bigger than the one in the surface. If the stratosphere doesn’t warm more than the surface, its temperature cannot be the cause for the warming of the surface, but rather a consecuence, as it happens under El Ninos or solar forcing scenarios.
I’ve been unsuccessful in accessing ftp://ftp.cmdl.noaa.gov/ccg/co2/trends/co2_mm_mlo.txt though I can access the Google cache. Does anyone else have any problems in accessing this file?
68 (SteveM): no joy for me either
Beaker, there is no real reason why anyone should use standard deviations for model runs unless the normal distribution is both proven and meaningful. But there are far too few runs and the uncertainty bars in the inputs are far too large for that. Furthermore, when multiple runs tend to converge it is mainly because of the same climate sensitivity assumption and similar “best guesses” for the important parameters. This combination of limited runs, huge uncertainty on the input and inbuilt biases means that every run should be considered as likely (or unlikely) as any other – no bell curve, no sd. The locus of uncertainty is actually even larger than Gavin shows because the full range of the input uncertainties are never tested – (ie you would certainly get cooling under some aerosol scenarios).
The only runs useful for validation purposes are the ones which get the surface trend correct and the only truly useful validation test is against real world data. That is the crux of the Douglass et al paper as J. Christy said above. This is how computer models are usually tested. In 22 years of computer modeling I’ve never come across the RC conclusion that large overlapping uncertainties can validate any model. It’s preposterous!
66 (Boris): Tropical Tropospheric amplification seems to be a distinct GHG finger print. While it may be true that trends are amplified from any forcing as you go up higher in the atmosphere according to models, the GHG pattern is distinct from the others. If you look at figure two here Solar does not seem to show the same amplification. Sorry I can’t give a better ref, but that source has lotys of refs (and I think you can swim through his editorializing).
In agreement with JOhn Christy’s point about higher tropospheric temperature variance, Santer et al Sci 2005 Abstract also state:
John Christy mentioned that the 1.2 ratio was GLB and that the tropical ratio would need to be checked separately. I did a quick check on the ratio of the standard deviations of the two tropospheric series to my calculation of CRU tropical (as shown in #19 above) and obtained the following ratios:
So the variance scale of the satellite plots using 1.2 is a bit larger than the adjustment that would be yielded by the above standardization, but not enough to change the impression of the graphic. It’s interesting that the standard deviation of RSS is larger than the standard deviation of MSU.
Andrew says:
This is only one of the more minor points raised in the RealCLimate article, the use of the standard error of the mean and lack of error bars on the observational data is likely to have a far greater effect on the statistical test (and therefore the validity of any falsification). As far as I am concerned, the conclusions reached by Douglass et al. are questionable, to say the least, until these more substantive issues have been addressed.
66: Re: Tropical tropospheric warming as a distinct GHG fingeprint. Look at the AR4 Figure 9.1 and the CCSP Report mentioned above Figure 1.3 on page 25. Both show hindcasts simulating 20th century (or latter-half 20th C) climate change in piecemeal forcing-by-forcing steps as well as the total. None of the forcing changes yields an amplified tropical tropospheric warming pattern except GHG’s, and the GHG effect is so large that the GHG-only panel is just about identical to the sum-of-all-forcing diagrams.
Then look at AR4 Figure 10.7, all model runs available here. These are for medium-level GHG increase rates. All model runs without exception show a strong amplified tropical tropospheric warming trend.
The accompanying text in the AR4 (pp 764-765) states
As to the question of what you have to do to eliminate the warming in the tropical troposphere while allowing GHG’s to rise, in other words to generate an overlap between models and observations, the CCSP (p. 11) states, in discussing a figure that showed the data-model discrepancy:
(For those of you with a philosophical bent, it is worth pondering the situation in which model parameterizations yielding the greatest agreement with the observations but the least agreement with the modelers’ prior hypothesis are parenthetically dismissed as “probably unrealistic”.)
It appears to me that one cannot disavow tropical tropospheric warming as a necessary implication of the overall GHG hypothesis without thereby disavowing the current structure of GCMs altogether.
As for stratospheric cooling, the RSS record is graphed here. I see 2 steps associated with volcanoes, but flat in between, and flat since 1994. The trend line obscures this. I do not see a steady cooling that would correlate with rising CO2 levels, but perhaps this has been addressed in print somewhere (I have not looked).
Andrew,
Ah, I see what’s wrong with Monckton’s interpretation of the figure you cite.
The figure shows the contributions from the various forcings, and then the total effect of all forcings combined. It does not attempt to show various forcing fingerprints.
Here is the actual caption from the figure Monckton uses:
As you can see, this has nothing to do with “fingerprints” or “signatures.”
JamesG says:
Testing whether some observations are consistent with the model runs requires a measure of the spread of the model outputs. The standard deviation at least has the benefit of being a measure of the spread of the data; the standard error of the mean does not. If we had an infinite number of models then the standard error of the mean would be zero, but that would not mean that there was no spread in the outputs (i.e. zero uncertainty). You can argue whether a Gaussian approximation is reasonable or not, but the fact remains that the standard error of the mean is the wrong statistic. The standard deviation is still a sensible measure for non-Gaussian data via Chebychev’s theorem, which IIRC broadly states that 75% or more of the data lie within 2 standard deviations of the mean (almost) regardless of the distribution.
It is also a concern to me that the distributions for both the observed data and model runs may be assymetric, in which case it is possible that the error bars overlap even more than indicated (or indeed less). However, since it was Douglass et al. that were attempting to falsify the models (a laudable aim), it is for them to establish the adequacy of their distributional assumptions.
The point RC were making was not that the data validate the models, but that they didn’t invalidate them. That is not the same thing at all.
#68 SteveMc
Just tried the link and it worked perfectly fine. The data goes to March 2008.
Ross,
See my #75. Figure 1.3 from the USCCSP report is essentially the same as the IPCC’s figure 9.1, except that 1.3 is a run of forcings from 1958-1999 and 9.1 is from 1890-1999.
The reason that solar shows no fingerprint is because TSI has not changed much, and thus has not caused much warming. As noted in the RC article I referenced earlier, when you run a GCM with a 2% increase in TSI, you get hotspots just like the GHG pattern–except for the cooling stratosphere with GHGs, of course.
Re: #74
That is why we need a show of hands from the AR4 contributors on the separated parts of matters like the tropical tropospheric warming in attempts to avoid apparent contradictions and complications. That way we can have or at least appear to have more certainty about the uncertainties involved in climate modeling overall and yet be able to invoke uncertainties where required.
Beaker, here is something I don’t understand.
The error bars that RealClimate calculated for the models in response to Douglas et al are here: http://www.realclimate.org/index.php/archives/2007/12/tropical-troposphere-trends/langswitch_lang/sw#more-509
Now, if I’m reading their chart correctly, their lower error bar shows a warming trend at the surface of something like .025 degC/decade, or .25 degrees per century, or 1 degree every 400 years.
So, in calculating a spread of the model’s output that shows they are not inconsistent with the troposphere data, have they not also shown that they ARE inconsistent with the surface data? Or are they saying there is so much error in the surface data that the actual change in surface temperatures over the last century could really be as low as .25 degC?
Or am I missing something obvious here?
#77,69. It’s working for me now as well. Must have been a temporary glitch.
Michael Smith says:
No, as far as I can see the observed data for the surface are also within the error bars (computed using the standard deviation), so they are consistent with the models. Note consistency does not imply support, it just means that the data don’t invalidate the models.
To pick an example, in the Schmidt-HAnsen model, can someone tell me what would be the tropical troposphere temperature increases for doubled CO2 – apples to apples, as best as one can tell, relative to what RSS and MSU are measuring?
But Boris, we are not asking an in-principle question. We are not interested in whether a huge increase in solar output could, in principle, create a differentially strong tropical tropospheric warming (and since the IPCC argues elsewhere for extremely low solar influence it would have to be exceptionally large). We are interested in whether the observed historical changes could create such a fingerprint. The answers in the cited figures are: GHG Yes; Solar and all others No. In other words, according to the parameterizations in those models, the observed forcing changes over the 20th century ought to have produced a strong tropical tropospheric warming trend, attributable only to GHG (since the other changes were too small or weak to do it), and it should be observable by now. Its absence therefore has no obvious implications for understanding the solar, volcanic influence etc., since the hindcasts suggest they were never candidates to explain it anyway. The message of those figures is that the absence of a differentially strong tropical tropospheric warming trend tells us something about GHG’s.
The graph “buster” below from RC is what I was looking from Beaker. If one adjusts (lowers) those big black dots to fit the model at the low to surface elevations then the black dots at the 700 and 500 pressure heights would appear to be outside the model minus 2 sigma limits. That says nothing about the uncertainty of the instrumental measurements, but interesting none the less.
Beaker,
I take it the next time an alarmist cites “models” to refute a skeptic, you will back the position that the skeptic’s point of view is within the model’s range of possibilities?
Re #67
This is ‘not true’, the upper stratosphere will cool with the increase in GHGs (mostly CO2), cooling in the lower stratosphere has mainly been due to the reduction in O3
Figure 1. Tropic (20S-20N) temperatures in deg C. All data shown to March 2008
Wow, I’m glad I live in NJ, I had no idea it had got that bad down south! 😉
Steve: Playing the pedant today? Anyway, I had to put my toque and winter coat on today in Toronto. A little Arctic blast.
Ross,
The issue I was addressing is whether significant tropical tropospheric warming is a “fingerprint” of GHG warming.
Steve M says:
And I think this is wrong. Tropical tropospheric warming is a fingerprint of warming–whatever the forcing. So if there is some discrepancy between models and observations, it does not disprove GHGs as a cause of the warming, but it would suggest that we know a good deal less about the tropical atmosphere and the lapse rate than we thought. It doesn’t tell us anything about GHGs specifically.
In short, even if there were enough data to properly evaluate the models vs. observations, a discrepancy would not be a blow to CO2 warming specifically, but to our understanding of tropical warming more generally.
re 83. there is an online database of the hindcast 1880-2003. but you gotta
work by hand
re 89. what boris said. However, it comes with a flipside. So, One cannot point
to TT warming as evidence for or against AGW. Boris?
Essentially your argument is this if it goes up our hypothesis is bolstered.
If it goes, down, we were not wrong, we just need to fiddle with the theory.
All of which means these observations cannot falsify the theory. So. what to make of that.
shrugs.
RE: Boris #89 and Kenneth #85
At what point now do you suppose that the two sides can agree that there is divergence between observations and prediction models? 2 standard deviations are required to “place” models within observation. What re-calibration efforts are being made right now to get any of the current models (which we shall say are now “aggressive” wrt to the effects of CO2 forcing) to fall within at least one standard deviation? I have done a cursory look for any published rebuttal to Douglas et al., I haven’t found one yet. Perhaps someone might know of one.
Not sure what it tells us about GHGs but it seems to be telling us something about the models.
#90. That’s a different number than their doubled CO2projection. For example, in the figure http://www.realclimate.org/images/2xCO2_tropical_enhance.gif they show a hot spot in the tropical troposphere color coded only to the range 3-14 deg C. Presumably there is underlying data that equates to the UAH/RSS troposphere. You’d think that SChmidt would have calculated the USH/RSS equivalent for comparison. PErhaps he has somewhere.
85 (Kenneth Fritsch): Those error bars are ridiculous! Couldn’t they have graphed them so they looked less insane?
I think that there are different ways of interpreting the tropical discrepancy, if we except it as real. Boris is trying to imply that it really means we don’t understand the tropical atmosphere. Well, forgive me for being blunt, but isn’t it kind of important to correctly model the area of the atmosphere which is so important for getting the WV and cloud feedbacks correct?
Of course, Singer’s claim (that it falsifies AGW) is probably too strong.
Boris, if the IPCC and CCSP authors had intended to argue that differentially strong tropical tropospheric warming emerges as a result of all types of change, they could have done so, but they didn’t. They argued the opposite. They showed that the observed historical changes in non-GHG forcing agents are not expected to lead to differentially strong tropical tropospheric warming, in the case of solar, volcanic, aerosol etc. But observed historical GHG accumulation is expected to have generated differentially strong tropical tropospheric warming, under the hypothesized model sensitivity. The failure to observe the predicted pattern therefore refutes something. Either GHG’s didn’t actually accumulate, or they did but they didn’t have the predicted effect, or one of the other changes offset it. Since the data show GHG’s did actually accumulate, the first option is ruled out. Nor can you say they accumulated and had a strong effect but other changes offset it, since in the all-forcings summation the net effect is still strongly positive in the tropical troposphere, indicating the other forcings were not strong enough to offset it in the models. The remaining option is that GHG’s accumulated but didn’t have the predicted effect.
It won’t do to try and excuse the discrepancies by saying that they only show we don’t really know how the mechanism works, if you also want to say that we are certain the mechanism works the way we have always said it does. You can’t have it both ways. If the mechanism really works as embodied in the GCM code, the data apparently imply very low GHG sensitivity. If you want to argue high GHG sensitivity + no differentially-strong tropical tropospheric warming, you’ll have to come up with some other mechanism than what is currently in the GCM code. In other words, to disavow the prediction of differentially strong tropical tropospheric warming, you have to disavow the current structure of GCMs.
Steve Mosher, Hansen/Schmidt have outputs here
http://data.giss.nasa.gov/cgi-bin/cdrar/do_LTmapE.py
http://data.giss.nasa.gov/work/modelEt/time_series/work/JTmap.txt
These yield T2 and T4 for the benchmarking. It is inconveniently reported in a binary format (though they’ve provided a Fortran script.) Does anyone know how to read the binary format into R or ASCII?
@87 (Phil), @67 (myself)
Sorry Phil, wherever you read “stratosphere” in my post, I really meant “troposphere”. I chose the wrong word for unknown reasons. I’m still wondering why, as I knew well what I was talking about.
Beaker, in 82 wrote:
Yes, you are right, the surface record falls within the calculated error bars. The question is, what justifies the inclusion of models inconsistent with the surface record in the calculation of those error bars? Or to put it another way: What justifies using models that are wrong about the surface to cover for models that are wrong about the troposphere?
SteveMc(97)
The first link doesn’t work for me.
#100. It’s typical GISS; you have to regenerate things. Don’t worry about it, it doesn’t give forecasts anyway.
95:
Actually, I’m not arguing this. I disagree with the Douglass analysis for reasons outlined at Real Climate. If the Douglass analysis turns out to be right, then it would mean we don’t understand the trop. trop. I don’t think this would have a huge effect on our understanding of CO2 warming, but it could indeed have an effect.
Remember that climate is weather over a time over an area, and some events appear to be half weather and half climate (which is how I’d describe the large-scale repeating events).
Now about the “potentially flawed observations”. If you can’t trust the measurements and physical observations, how can you possibly trust something that’s modeling it? That makes no sense. Do the models show what reality does?
Thanks to John C for that gem; if you can’t falsify your hypothesis, it’s not a hypothesis now is it? That’s the first thing anyone should do, but instead, it’s not done at all, it seems to me.
Ross,
Your last sentence comes closest to the issue. If the Douglass analysis is correct and the tropical troposphere is not warming faster than the tropical surface, then it’s not just GCMs that are wrong, but also theory (from RC):
I assume a word is missing between “something” and “to,” perhaps “limited.”
Boris,
No, the the observations can be explained within the bounds of well established physical meteorology if the relative humidity doesn’t remain constant with temperature. If there is no increase in water vapor partial pressure, the lapse rate doesn’t decrease and theory and observation agree. Of course then there is no water vapor feedback and climate sensitivity will be at the low end of the scale.
Boris, this is why I think the cost of climate policy should be calibrated to the mean temperature in the tropical troposphere, a la the T3 tax. If strong warming doesn’t appear there, then the case for incurring the costs of major GHG abatement likewise fails to hold up.
Economists were once wedded to Keynesian macro models, but the emergence of stagflation in the 1970s, and the failure of deficit spending to yield GDP growth in the 80s, refuted the models since they predicted the opposite would happen.
Regarding GCMs, Soden and Held wrote in 2000:
Held, I. and B. J. Soden (2000) “Water Vapor Feedback and Global Warming” Annual Review of Energy and Environment 25:441—75, page 471.
We are near the ten-year mark since they published that. I think the failure to observe differentially strong tropical tropospheric warming, and the absence of stratospheric cooling since 1994, are significant facts.
And if theory is wrong, does the world come to an end? Not for rational people, no. Rational people go back to the data and come up with better theory.
I am very perplexed by the various comments. If the lapse rate for the tropics from the models doesn’t even resemble the measured data, what difference does it make that the measured values fall within the model error bounds – except to tell you that the model error bounds are huge. If the model error bounds are huge now, why should anyone believe what the models predict for 100 years in the future ? Can the model error bounds decrease with time (considering that the models are nonlinear, complex, probably chaotic, and only constrained from exponential growth by artificially applied damping) ? All the noise about Monte Carlo runs being used to project 100 years into the future assumes you know something about the parameter statistics – improbable, to put it mildly. To me, at least, the different shapes in # 58, graph, say that the models are both incomplete and presently wrong. Projections into the future are useless unless the models can replicate the present. I also find it entertaining that it seems to be increasingly difficult for anyone to articulate what AGW is (no more moving targets). Sure, we all know that increasing atmospheric CO2 is BAD, VERY BAD. Just hand over complete control of worldwide energy usage and you won’t have to worry about it anymore. Thanks, but no thanks. I’m not worried about CO2 increases, anyway. The global temperature is dropping rapidly.
96 Ross M
An excellent summary of the situation, very clearly stated. If the thinking of everyone were as clear, we would all make faster progress in resolving this issue.
To paraphrase the great Douglas Adams – “The theory is authoritative. When it differs from reality, it’s reality that’s got it wrong.”
Mr Mc.
This might help for binary conversions–BTW, I have scanned with Symantec Corporate AV and detected no viruses.
http://www.gdargaud.net/Hack/BinToAscii.html
you asked a Q over at lucias, my Link to the Model data is there.
I tried to register a while back to get the data, but I was curt and
they were snotty. It’s a cartoon show now. “curt and snotty”
So you can go to the place I linked to
register and get the data.
102 (Boris): Please read what I say very carefully next time, because I specifically added that caveat. I know darn well you don’t believe their analysis.
115:
I’ll promise to read mroe carefully if you promise to write more carefully. 🙂
116 (Boris): Okay, I’ll see what I can do about that.
Regarding the T3 Tax, the formula to calculate it sure is complicated for such a simple idea.
Click to access T3tax.VV-online.pdf
But in RC world, it would be able to simultaneously be a tax and a subsidy. Now that would be something! I guess that rather than calling their bluff he has exposed their incredible ability to dodge an unpleasant conundrum. Oh well, nice idea anyway…
Phil says:
The upper stratosphere also has no water and very little matter so we would expect to see a response that closely matches the basic radiative physics built into the models. The same radiative physics with no water feedback will give us warming in the troposphere of around 1.5 degC per doubling. We have nothing to worry about if that’s all the warming we will see.
This means the cooling the stratosphere tells us nothing about whether the models are reliable predictors of climate in the troposphere. That said, I would like to see some comparisons between the actual cooling in the stratosphere and the models but I can’t find any that are not behind a pay wall. In addition, it would be important to look at the tropospheric trends for those model runs that most closely match the actual upper stratosphere cooling. If the models with the best matches in the stratosphere have a poor match in the troposphere then the models are not very good.
117: Andrew, a 3-year moving average is not all that complicated. BTW, when I wrote that chapter last year the T3 tax rate was $4.67. It’s now $3.33 and falling. If this trend continues it could indeed become a subsidy, but to oppose it on the grounds that it might end up as a subsidy for CO2 emissions is to admit that one actually expects global cooling.
119 (Ross): I’m referring to RC’s claim that the modeled and observed trends overlap within uncertainties (or something). If we were to apply that, even a complete absence of warming in the tropical troposphere would be “consistent” with the models, so in RC world, your supposed to look at a range of values, hence, it would easily be possible for them to say that due to errors (that they won’t identify) in the data set, when it appears to be a subsidy, they would say it really should be a tax. Crazy, huh? It’s like the laws of thermodynamics with those guys. (Kudos if you get that).
#85
I got a kick out of a graphs where the uncertainty is so large that the sign can be wrong and the answer still right. Also suspicious is that the number always falls on the same wrong side of the line.
#113. Steve Mosher, I don’t doubt that the information is there somewhere. CAn you give me any guidance on how to find these particular data sets in the forest?
Well, I just took a look at the numbers from the Douglass et al. study.
All of the talk of error calculations and confidence intervals misses the point. Regardless of the error limits, if we can reliably tell the difference between a model result and the data using some simple heuristic, the two sets are different. All that error calculations do is let us do this (determine if the datasets are different) by standard statistical calculations. This is important if the answer is not immediately obvious.
But that’s not the only way to tell a frog from a moose. Yes, we could get 20 moose (meeces?) and 20 frogs, and weigh them, and see if the confidence intervals of the mean weights overlap. Or, if we are just dealing with frogs and meeces, we can use a much simpler heuristic – if it weighs more than 20KG, it’s a moose.
And in fact, with the Douglass data, the change in trend from the surface (or the lowest observations) up to 500 hPa can be used as such a heuristic. If the trend is less at 500 hPa than it is at its lowest level, it’s data. If the trend is greater at 500 hPa than at the lowest level, it’s a model.
Of all the data and models, the only mistake is that this heuristic mis-categorizes a single model. It is the Russian model, one I’d never heard of before, and one which is wildly different from all the rest of the models.
In fact, this is a very good heuristic because it highlights the essential difference between models and data – with the models, as you go up from the surface, the temperature trends increase. With the observations, the temperature trends decrease with altitude. Since the observed trends have to increase (and increase strongly) if the AGW hypothesis is correct, I’d that particular myth is busted …
w.
PS – I loved this part of the Douglass paper …
Yeah, I guess having an atmosphere below the surface is “unrealistic” …
PPS – Beaker, you say:
First off, depending on RealClimate for information about statistics is like … like … well, I can’t think of a metaphor that’s suitable for a family blog, so let me just say it is a very risky thing to do.
Second, you AGW guys can’t have it both ways. You keep telling us that an average (ensemble) of models is much more accurate than the individual models. If this is true, then it means that the models fall in some kind of quasi-normal distribution around the “right answer”, that is to say, the answer given by observations.
But if that is the case, then certainly we are justified in using the standard error of the mean to put bounds on what the ensemble of models say the “right answer” is. This is done by calculating the standard error of the mean of the model results.
If you want to claim that this is the wrong way to go, then there is no point in using a model “ensemble” at all. The only way that the Douglass et al. calculation using the standard error of the mean could be wrong is if the models in fact do not cluster around the “right answer” … are you sure you want to go down that road?
But assuming you do, then you’ll have to tell us how to do it. So given two datasets A and B, we want to determine if they are drawn from the same distribution. The usual way to do this is to see if their confidence limits overlap, which of course uses the standard error of the mean … but you say you don’t want to do it that way.
So … please explain to me how we can mathematically show that they are or are not from the same distribution without using the standard error of the mean of the datasets …
I have watched a lot of scientists argue over which models best fit the data, but I have never before heard anyone argue that all of them are right because the spread in the models encompasses the data. No one expects models or data to be perfect, indeed perfect matches usually raise suspicions, but they do expect general agreement of a model over a wide range of the data for the model to even be in contention in these arguments. Thus the errors go on the data, and the models that stray far from those bounds are either reanalyzed to find out what went wrong and adjusted, or thrown out.
But, we are not really talking about models. We are talking about individual simulations. These are distinct sets of ICs and BCs that are run through specific models. If one had the computing power, one could Monte-Carlo an appropriate range of conditions and come up with a corresponding spread of predicted outcomes for a specific model and look for reasonable overlap with the data. (Like getting the error range for each 100 year forecast.) But unless you have done a really good job, you have probably only calculated a subset of the total spread possible. So such an analysis is on shaky ground. It is much better to look for and test consistant characteristics of the model, like those Douglass attempted to test. I am not sure if lumping all the models together is advisable for such a test, but you work with what you have.
Isn’t this just equivalent to replacing the ensemble with a simple model that generates a broad range of values that encompass the entire data set?
Willis Eschenbach
Well as it happens I am well qualified to comment on the statistics for myself and noticed these errors for myself before the article appeared on RealClimate, so I am not depending on RealClimate for this one. However, if you can’t refute the argument, then an ad-hominem is a poor substitute, which I personally would avoid.
If I understand it correctly, much of the variation within the ensemble is stochastic noise (i.e. differences in the “simulated weather”), in which case the mean gives the best estimate for the underlying climate, having integrating out the weather. The spread of the ensemble gives an indication of what is possble for a stochastic realisation of that climate. The observed weather IS a stochastic realisation of an underlying climate forcings and feedbacks, which is why it is reasonable to see whether it fits within the spread of the model runs rather than the error bars for the mean.
If the observed data was a pure indicator of the climate, you would have a point, but it isn’t. It is corrupted by weather.
Peter Thompson says:
Of course, it would void the refutation. However, in the interests of balance, I would be just as quick to point out that the ensemble distribution includes some possible outcomes that might support the “alarmist” with a similar level of plausibility. If those involved in the debate were more comfortable with uncertainty, rather than taking a polarized stance on one side or the other, it would be much more productive. The bottom line is that the models suggest a variety of outcomes, with differing levels of plausibility, and you have to consider both the plausibility and the likely impacts of a particular outcome to determine whether it is of importance.
Michael Smith says:
I think the reason the data are within the error bars is because the standard deviation is used rather than the standard error of the mean, rather than the selection of models. This alone makes the error bars about four times broader. I can’t really comment on the climatology, as it isn’t my field, I can only comment with confidence on the statistical issues.
I have just skimmed the Douglass et al paper again, but I couldn’t find the part that explained how the models that were inconsistent with the surface data were identified. If it was done using the standard error of the mean, then that test is also incorrect. Sadly the aim of Douglass et al. was a good one, validating/invalidating models is important in developing understanding, but sadly the statistcal errors mean the paper is probably doing more harm than good. I do hope there will be peer-reviewed correspondence in the journal to resolve these issues (a part of scientific method that is sadly lacking in the modern era).
“…it is to be emphasized that, in several cases, qualitatively different behaviours emerge among the models: often, the ensemble mean does not correspond to the output of any sort of average model, as the ensemble mean falls into nowhere’s land, i.e., between the clusters of the outputs given by the various models. This suggests that the usual procedure of merging data coming as outputs of various models is much more problematic than commonly thought.”
an excerpt from a guest weblog by Valerio Lucarini in Climate Science.
Beaker you might use Chebychev’s theorem for real world data but for these model outputs you shouldn’t, unless – as was suggested above – you had done a random selection of parameters for the inputs. Otherwise the output reflects only the biases of the modeler. (Eg a climate sensitivity of 3 degrees is an inbuilt biased assumption which clusters the output around what the modeler “expects” – classic circular reasoning). A true range of uncertainty in the output, using the true range of uncertainties of the inputs, would be a lot larger than that shown by Realclimate, which of course would be equally meaningless. You are certainly correct that we have to use some measure to test the model outputs but regardless of how wrong you think the Douglass et al. test is, using standard deviation as a measure is surely worse. The usual technique is to look at each and every model output and judge them on their own merits or demerits. Only in this way can we tell which assumptions were more correct. Stats doesn’t help – you need a human brain. If a model run doesn’t agree with the observational data, a competent modeler should try to find out why. Conversely, anyone looking for an uncertainty range of an ensemble of biased model runs tells me only that the modeler is operating in a reality distortion zone.
John Christy:
Cry FOWL and let slip the chickens of WAR!
Beaker: “If I understand it correctly, much of the variation within the ensemble is stochastic noise (i.e. differences in the “simulated weather”)”
You don’t. There is no weather noise in the climate models. The only noise is due to too large grid elements or too large timesteps. So you just are making things up to support your own bias. Easily done I admit.
Ok that is just astonishing.
Re: 126 beaker
You say:
I think if you spend a little time studying this document: An Overview of Results from the Coupled Model Intercomparison Project (CMIP) ( http://www-pcmdi.llnl.gov/projects/cmip/overview_ms/ms_text.php ) you will find that what you are calling ‘simulated weather’ is actually only a difference between models. For a quick look, see figure 1 (model ensemble performance without forcing), figure 2 (model ensemble performance with 1% CO2/year) and figure 20 (global averaged difference between increasing CO2 and mean surface temperature). Please note the range of ensemble values given for mean annual temperatures. Also note that CMIP had no problem comparing ensemble mean with observed temperature, as a point of ensemble validation.
The problem with Gavin’s standard deviation is that it uses an ensemble outlier (lowest) as as the data for the calculation. Which brings us back to Willis’ observation: Why use an ensemble at all?
Cliff
JamesG says:
That is not correct. The weather system as modelled is chaotic, which means given the same climate forcings and feedbacks, you will get different model ouput every time you run the model. This variation represents different stochastic realisations of the “simulated weather”. These can be averaged across model runs to give the climate.
BTW, I would be interested to know what evidence you have of my bias in that all I have done is point out that one paper has a statistical flaw that invalidates its otherwise commendable aims.
Re # 42 Willis Eschenbach
You are much closer to modelling progress than I am. (At the end of my full-time work I was more used to approving or not approving projects submitted, than innovating). Is there any formalism, any progressive evaluation, any set of criteria that say “This modelling should be stopped because we have failed to meet stated criteria?” My personal feeling is that some of the remaining identified problems might be known to be intractible and therefore much of the modelling should be stopped. Have we reached that stage?
Cliff said:
The standard deviation is calculated in a similar manner to the standard error of the mean, but for the factor of sqrt(n). If the standard deviation depends on an “ensemble outlier” (it is not clear to me what this means) then so is the standard error of the mean used by Douglass et al, and so it also shares this problem.
Surely the spread in the ensemble reflects the uncertainty in our understanding of the underlying physics (as well as the stochastic nature of the simulations themselves). If we want to compute the value of some variable of interest, then the proper thing to do from a Bayesian perspective is to integrate over this source of uncertainty (i.e. marginalisation). Why settle for an approximation (the mean) when averaging over the ensemble is more sound?
Briggs has a post on ensemble-ing stuff Why multiple climate model agreement is not that exciting.
Nope, until the models/codes/applications have been subjected to Independent V&V and maintained under SQA we don’t know what the numbers represent.
Re: 136 beaker
You say:
A major problem with your view of the ensemble model ‘weather’ effects is that the model data in Douglas et al that we are discussing are trends from 1979 to 1999. It is a stretch to say that there are weather effects in a 20 year trend. You did read the paper, didn’t you?
You say:
My point on ‘ensemble outlier’ was that the error bars are inflated by that uncertainty of understanding, when the whole point of using an ensemble was to cancel out that uncertainty. My guess is if only the ensemble model member with the the lowest trend value (at each altitude) is used to calculate the standard error, the results with respect to overlapping the observed data would be similar to Gavin’s result. At that point the only purpose of having an ensemble is to be able to pick what ever member makes, whatever point you want to make, wherever you want to make it.
Cliff
A GCM output is averaged over many runs to remove the noise and identify the climate. The climate itself has made only one run, but it has produced many years. So, if a model were any good, the climate should bounce around its average due to weather. Yet it does not. This implies at a minimum that there is some redness in the climate that nobody in the AGW world has a clue about.
But the main problem with your analysis is that the models are tuned to produce somewhat realistic values. I don’t think there is a model that works from first principles. Naturally they are going to be in striking distance of reality. Unless somebody can tell me that no model in the RealClimate “ensemble” is free of “Flux Adjustments.”
Cliff Huston says:
As I understand it, for each model there are a number of runs with the same forcings. The output of the models are stochastic realisations of the same underlying physics. This stochastic variation causes variability in the estimated trends. Perhaps calling the variation “weather” is a little loose, but the point remains that the spread of the ensemble for a given model reflects the plausible varaiation in the trend that is consistent with the physics of that model. If the obseverved data is within that spread then it is consistent with the model.
Consider this, I can make a computer model of a six sided dice (e.g. using the random number generator in MATLAB). I can then make n ensemble of 100 model runs, and I get a mean of 3.68 with a standard error of the mean of .1601. Now I roll a real dice and get a 5. Does this invalidate my model of the dice because the observed data lies outside the error bars giving +- 2 times the standard error of the mean? No of course not! Does the value 5 lie within the spread of the ensemble? Yes it does.
Ah, I see where you are coming from. The point is that the observed data is also only one stochastic realisation of the actual climate forcing. Given a different sets of initial conditions, we would see different values for the observed trend. Unfortunately we can’t cancel out this stochastic uncertainty in the observed data the way we can with an ensemble because we have only one realisation of reality. What we can do is see if this one realisation is plausible given the model, which can be done by seeing if it falls within the spread.
You are missing the point Douglass et al claim they have falsified the models, in the sense that the observed trends are inconsistent with the models, however the test the used only demonstrates (imperfectly) that there is a significant difference between the observed trend and the average over all models, which is a much weaker claim (in fact I don’t think it is in any way contraversial).
Of course any prediction that lies within the spread of the models is considered plausibly by the model. However, what you should do is marginalise over the ensembe to make predictions. Then there can be no accusation of cherry picking.
A remake of “if observations don’t fit models, it’s the fault of observations”.
Beaker: If you don’t believe me then perhaps then you’d like to discuss weather noise with William Connolley, who recently reassured us all that weather noise is most definitely not in the IPCC projection ensemble. I acknowledge that all models are different and some behave better than others (eg coupled models, carbon cycle models) but the IPCC ensemble do not constitute the more advanced models, as you appear to assume. They are important only because they are being used to direct policy. In any event assuming that a simulation of random behavior represents weather, then assuming that combining them represents climate is rather facile. Frankly it cheeses me off when people talk about stochastic or Monte-Carlo methods when they really mean “random”. All such random methods are just a poor substitute for real knowledge, so they truly need independent testing before being relied upon. Stochastic is actually Greek for “guess”: I prefer the English word. But if you want to combine the ensemble into one averaged run then fine. Comparing that result with observations doesn’t fare any better. As for using a “Bayesian perspective”, too often in science I have have noted that can be translated as “let’s give a high probability to our guesswork”. I assume bias only because it’s a difficult thing for all of us to avoid, but if I offended you I apologize.
beaker, my apologies if I offended you, I meant no ad hominem, my bad.
Now, here’s the thing.
AGW theory says that as you go up from the tropical surface, the temperature trends will increase. So, let’s start all of them at the same spot, the actual surface trend, and see who does what. No error bars, no averages, just the raw data. Here it is.
Now, there’s a few things of note here. FIrst, all of the models save two outliers rise fairly steadily from the surface to around 200-300 hPa. The two outliers are strange. They don’t look anything like the other models. So I’d say that, although not quite everybody got the memo, the climate models definitely agree with theory, they say that the tropical temperature trends increase with elevation.
The data, on the other hand, all decrease from the surface (or their lowest point) upwards.
So, beaker, you can make any statistical claims you want. But it is clear from that chart that a) the models almost all agree (twenty out of twenty-two) on a rising temperature trend with elevation, and b) none of the four datasets shows a trend anything like that. Like I said, there’s more ways than statistics to tell a frog from a moose.
w.
I love that willis. all the models say heads. the data says tails. Modeler response.
we meant heads +- tails. seriously which is m22?
Steve: INCM.3.0 Institute for Numerical Mathematics, Russia
This is nonsense. If the weather isn’t averaging out to your climate model over time, your model is wrong. Full stop. You are like my brother when he lost a cgame as a child, he would say, let’s go two out of three, then three out of five, until finally even he agreed that it was ridiculous.
And here I thought that the weather was what we were getting the observed data from. Maybe I am just a little slow today, but if the observed data is not from weather, then what is it from?
beaker, I understand your point about comparing the distribution of the mean to the distribution of the data. 1/N and all that. In this instance you want to say that the proper point of reference is the distribution of the individual model runs, which is now so wide that any conceivable data can be “consistent” with it. The CCSP tried on this fig leaf too. Here’s how they phrased it (p. 3):
Now step away from the statistics and just think about the overall logic. A supposedly fundamental aspect of the underlying mechanism is the tropospheric amplification. It’s in all the model runs, hindcast and forecast, shown in the AR4 and the CCSP. But faced with contrary data we get a Yes Minister style paragraph saying that with some tweaks to model parameters we can turn a GCM into a computerized coin-toss, where half the time it says one thing and half the time it says the opposite, and as long as we refer to this vacuously wide range there’s no possible conflict with any data. Does this strike you as a victory of the models? It sounds like an admission of defeat to me.
The thing about rolling a dice is that you have no prior information about the outcome, within the range of possibilities. Likening models to dice is saying the models are uninformative. To put it another way, policy makers have come to believe that models are informative, in that they all concur on a specific explanation for historical warming and a specific set of predictions for the future. This is the language of the IPCC SPM. They have NOT come to believe that the message from the modeling community is that “anything could happen” and – as in the dice example – any outcome is equally likely; i.e. it’s just as likely that GHG have no effect as that they have a big effect. There is nothing even remotely suggestive of this view in the IPCC report. So to invoke it now as a defence against contrary data sounds like special pleading.
If modelers want to use the mile-wide confidence interval defence, then at least recognize the corollary. So you have a hundred model runs, and a few of them way over there on the end are not inconsistent with the data. Can we see those model runs given the maximum prominence from here on in? Why do we keep seeing reports in which model runs totally at variance with the tropical troposphere are weighed equally as heavily as those not at variance, for the purpose of describing the likely future?
To be specific: What would the SPM Figure 5 look like if it only used model parameterizations and runs that were consistent with current data concerning the tropical troposphere? I conjecture that the scenario range would collapse to the orange (Year 2000 constant) line. The comment in the CCSS (see the quoted paragraph in #74 above) certainly points in this direction.
#3. Willis, is this a rendering of Douglass Table IIa. If so, the collation of Model 3 is missing some values over 0.6.
Willis Eschenbach says:
no offence taken, I just wanted to make the point that it is best to steer clear of criticising sources of data and concentrate on the specifics of the argument.
I am not making any statistical claims. I am just pointing out that Douglass et al. did not establish the result that they claimed because of an error in the statistical methodology. Nothing more, I thought climate audit of all places would be a good place to discuss that.
I can’t really comment on whether the breadth of the error bars on the models means that they are useless, I am not a climatologist, but as a Bayesian I am happy wth the idea of integrating over the uncertainty of the ensembe in making predictions about impacts for examples. I would hope this was done routinely, but the comments here suggest that only the ensemble mean is used, which is often a poor approximation. However, that is a separate issue.
Why do the two ‘outlier’ models do what they do?
=============================
I’ve uploaded Table IIa from Douglass et al 2007, which says that they have collated information on model outputs. Take a look at the column showing trends for 1000 hPA. Surely there must be a transcription error fora couple of the models. Model
3 (Canada)2(NCAR) shows a temperature increase of 1.5 deg C per decade! and Model 17 (France) shows a temperature decrease of -1.27 deg C per decade.That would seem to effortlessly bracket all conceivable possibilities.
I think that Douglass et al might have been more effective if, rather than trying to rebut “models” in general, they had focussed more on trying to trim down the reasonable universe of models.
I thinkk that there are two different types of uncertainty at issue – 1) a sort of stochastic uncertainty within the climate system i.e. that the same forcings might have a variety of results on a multidecadal scale (sort of long-term “weather”); 2) errors in our physical models.
Surely the experience of the past 30 years should be sufficient to say that at least some of these models probably have erroneous parameterizations in them. If we can’t, then how does one go about assessing this? For example, there must be something wrong with Models 3 and 17. Surely there must be an intermediate stage where reasonable people can agree on Models 3 and 17 without necessarily agreeing on how the “best” models are doing.
In this vein, surely one of the problems with IPCC is thir attempt to be all-inclusive. No national model ever “fails”.
#151. Good question. One of the HUGE frustrations with IPCC is that this sort of thing isn’t a central issue in AR4. It’s the sort of thing that interested readers wonder first.
JamesG says:
There is nothing inherently wrong with probabilistic reasoning, provided that you propogate your uncertainty in the inputs through to your conclusions. If you have uncertain data, you can only make uncertain predictions, however the laws of Baysian statistics at least give you a theoretically sound means of converting one into the other. I personally prefer a rigorous statistical approach over opinion.
No offence taken, I was interested because I had been very careful not to take any side in the wider debate in the interests of pointing out the seriour flaw in this one particular paper, which appears to be widely unapreciated.
Ross McKitrick says:
Douglass et al are making a statistical claim and I have been discussing their statistical methodology, which is flawed. It makes no sense to “step away from the statistics” as the statistics are the central issue in deciding the validity of their conclusion. If you don’t want to discuss the statistical flaws with me, that is fine, but I’d rather discuss the substantive issue rather than get sidetracked.
I could easily have made it a simulation of a biased die so that there could be useful prior information. The point of the example was to illustrate the difference between the standard error of the mean and the standard deviation.
Integrate over the uncertainty in predicting the impacts (i.e. take an average over the ensemble). In this way the impacts are weighted according to their plausibility under the model. Perfectly standard element of Baysian statistics.
Exactly, as I said, you need to propagate your uncertainty from your inputs through to your outputs.
re: Steve McIntyre, April 29th, 2008 at 8:25 am, who says:
Shouldn’t that be Model 2, National Center for Atmospheric Research, USA (NCAR)
Click to access DOUGLASPAPER.pdf
Beaker,sounds like you know your way around oncfidence interval estimation. what do you think of the use of calibration residuals in the proxy recons? Maybe you can solve a long-standing puzzle that has baffled UC, Jean S, Chefen, me and others – how the MBH99 confidence intervals were calculated?
#156. Quite so. Model 3 shows increases of over 0.6 deg C per decade at altitude. So it belongs on a critical list as well.
Steve McIntyre says:
Yes, I would certainly agree with that. It has become a high profile paper that many are using as evidence that the models are inconsitent with the data, which the paper has not established. However, I don’t think enough attention is paid to the spread of the model predictions either, a paper that integrates over every member of the ensemble in arriving at assessments of impacts would demonstrate this nicely by giving distibutions over the impacts that are a consequence of the distriibution of model outputs.
Thanks for putting that rather better than I did. Both forms of uncertainty are relavent in deciding if the models are consistent with the data, as the observed data is one realisation of the same form of stochastic uncertainty (but this time with the actual rather than modelled forcings).
I agree with Beaker in that Douglas et al. method doesn’t demonstrate what it wants to demonstrate due to an incorrect procedure. However I agree with Ross in that the defense of the models against Douglas et al. only makes the models look terribly inaccurate and wrong. Which, in the end, was Douglas et al’s point.
I can’t stop thinking “why did they leave it there?” I mean, if I had been defending the models against such an attack, I would have picked just one realisation of one model which agreed on the last 30 years surface trend, and at the same time showed the observed trend for the troposphere, and predicted warming for the next 50 years. Easy. Because it has to exist, won’t it? So, why didn’t they just show it to us and, instead, talked of the statistics?
In my opinion, this is most probably because:
1) There is no single model realisation which backwards-predicts, with reasonable accuracy, at the same time surface temperature trends and tropospheric temperature trends during the last 30 years, OR ELSE
2) There exists such a model realisation, but it only achieves such a result by showing big volcano eruptions and extreme El Niño or La Niña ocurrences which we know didn’t happen in reality, OR ELSE
3) There exists such a model realisation without including severe weather phenomena, but the realisation doesn’t predict some future 50 years of warming.
And 4) no matter how long they try, none of their models will produce the results which match reality.
It appears that “mining for the desired result” is applicable to more than just tree ring studies. It appears that one could throw a collection of models against the wall and pick the one that happens to match reality somewhat and claim then that the problem is better understood than it actually is.
By this logic, I could drop a box of toothpicks on the floor, pick the one that points closest to true north, and say that I have invented a better compass, from wood no less. Of course no one would accept this outcome unless I produced some confidence interval that said that it was impossible for the toothpick to point north by sheer chance, in my opinion, then couch it in the vestiments of mathematics.
Anyone who wishes to critique the Douglass et al paper can do so by submitting a comment to the International Journal of Climatology here:
http://mc.manuscriptcentral.com/joc
I made the same suggestion in December over at the political front for climate science known as ‘RealClimate,’ but my comment wasn’t published. I guess the crickets are still chirping on spurious RC criticisms being written up for submission.
Steve McIntyre says:
The proxy reconstructions look like a thorny topic to me, and I haven’t looked into it with anything like the depth that you have, so I wouldn’t presume to comment (other than that MBH99 carries rather less weight than others in my Bayesian posterior over reconstructions ;o). The field could do with more active involvement from statisticians IMHO. The problem with the Douglass et al paper however is much less subtle.
It’s worth remembering that if the modeled and measured surface trends match, it could very easily be for the wrong reason, especially considering what I consider to be the high likelyhood that the surface data have considerable contamination. Ross, can you give us an estimate of how much higher/lower the surface trend should actually be? I understand you had a paper on that. 😉
Even if the surface data is wrong, the temperature trends still decrease with altitude according to both satellite and balloon observations. So what are the trends in water vapor mixing ratio with altitude? This would seem to be the critical test. If specific humidity has been increasing, then it may well be legitimate to question the validity of the atmospheric temperature measurements, assuming the humidity date is valid. And if it isn’t increasing, then the idea of strong water vapor feedback becomes highly questionable.
DeWitt,
I cannot find any data concerning trends in such things as the mixing ratio, vapor pressure etc…
Some comment from Fred Singer:
1. Willis #49 (and some preceding by Judith Curry) talks about rapid convective processes ‘short-circuiting’ the GH effect and inadequate parameterization of this process in models.
If indeed rapidly rising cumulus strips out WV, then simple considerations of radiation physics will immediately lead to a negative feedback that’s not included in current models (see attached essay).
2. On error analysis of models: There is a conundrum I have pointed to repeatedly. We have 22 models with a total of 67 runs. However, the number of runs per model varies from 1 to 10. My question: How do assign weights when constructing an ‘average’? Do you give equal weight to each model or to each run – or neither? CCSP-SAP-1.1 seems to choose ‘models’ — see Fig. 5.4G
3. The CCSP graphs comparing models and observed trends don’t show any error bars. See e.g. Fig 5.4G. Yet now ‘experts’ from RC try to tell us that the data are uncertain.
4. This RC attack has focused on the MSU results from UAH, as requiring corrections. Yet Douglass et al [2007] rely on balloon data. Hasn’t anyone noticed?
5. In spite of the clear discrepancy shown [see again Fig 5.4G], the Exec Summary of the same CCSP report [written by Wigley, Santer et al] glosses over it and claims that there is really no disagreement. But have you noticed that they use ‘range’ to support their claim? Now ‘range’ gives undue weight to outliers at the tail of the distribution. In fact, one gets the paradoxical result that the more models (or runs) one uses, the wider the range – practically guaranteeing an overlap with the observed trend values and therefore removal of any discrepancy. Eureka – we found agreement!
Measuring Water Vapor Feedback
Climate models, without exception, incorporate a positive feedback from water vapor, which is the most important atmospheric greenhouse gas. One way this is done is by keeping relative humidity constant as temperatures rise, thus raising the WV content of the atmosphere and presumably the total radiative forcing. The effect of this positive feedback is to increase the ‘climate sensitivity’ by a factor of two or more compared to the forcing of carbon dioxide in the absence of an increase of WV.
It has been pointed out by a number of authors, apparently independently, that WV can also produce a negative feedback and thereby diminish the forcing effects of a carbon dioxide increase. One rather obvious mechanism is to assume that the increase in WV leads to an increase in cloudiness in cases where humidity and not cloud condensation nuclei [CCN] is the limiting factor.
A more subtle mechanism leading to a negative WV feedback involves the altitude distribution of water vapor, and in particular a drying of the upper troposphere [UT]. Different sub-mechanisms have been proposed to achieve such a reduction of UTWV. Hugh Ellsaesser assumes that warming of the tropical ocean will lead to increased meteorological activity and a strengthening of the Hadley Circulation. In turn this should increase the subsidence in the subtropical bands and thereby induce a ‘drying’ of the UT in those regions. William Gray has proposed a mechanism that relies on increased cumulus activity in the tropical region, where the downdrafts would occupy a greater physical horizontal area than the updrafts. Finally, Richard Lindzen has investigated a number of mechanisms, including what has become known as the “variable iris;” it also operates in the tropical region.
The theory of the negative feedback is rather simple from the radiation theory point of view, but quite complicated from the point of view of meteorology and cloud physics. If the UT is moist, then the outgoing long-wave radiation [OLR] in the WV bands will come from a cool region of the UT; but if the UT is dry, then the emission from these WV bands will take place from the much warmer boundary layer and make a correspondingly greater contribution to OLR. But since the total planetary OLR must balance, roughly, the incoming net visible radiation [incident solar radiation minus albedo], then emission from the surface to space, which takes place in the atmospheric window region [8 to 12 microns], must make up the difference. As carbon-dioxide levels increase, the contribution of CO2 radiation to OLR will decrease since it will now take place from a higher level of the troposphere — which is colder. (This is one of the conventional explanations of the greenhouse effect.)
In principle then, one can establish the existence of a negative feedback from UTWV and distinguish among different mechanisms by analyzing detailed measurements of the OLR as a function of latitude, wavelength, and time.
For example, under the Ellsaesser hypothesis the emission from WV bands should increase with time in the subtropical regions. For the mechanisms of Gray and Lindzen, the emission from the WV bands in the tropical region will increase on average.
Note that this method does not require actual measurements of UTWV, which are extremely difficult – and which can be misleading if one simply determines average values along a horizontal path from limb measurements.
——————————–
Comments are invited.
Best Fred
S. Fred Singer, President
Science & Environmental Policy Project
1600 S. Eads St, #712-S
Arlington, VA 22202-2907
Tel: 703/920-2744http ://www.sepp.org
Re Willis #144. Your graph makes me wonder how a similar graph of all the 67 model runs would look. It’s conceivable, depending on which models had multiple runs, that the same sort of pattern would appear. That is, all or most of the additional variability could occur above the observed values. The visual pattern of the additional variability in the 67 runs provides so much more information than just noting that the additional variability is larger than that of the 22 mean model runs.
Re post 144:
22 model predcitions are plotted. 20 of the models have tropospheric hot spots and disagree 100% with the observations. Two models partially agree with observations (say 50% of the time within the measurement bounds). Thus, one could conclude that 91% to 95% of the model predictions are incorrect. Whatever statistical test you employ, it seems significant most models are disagreeing with observations. I think that is the point that Douglass should have made.
Ross #148 “It’s just as likely that GHG have no effect as that they have a big effect. ”
Models telling us things, I agree. Reality, I disagree. It’s more likely the GHG have little to no effect, and it’s far more likely land-use changes, especially in the form of urbanization and heat and pollutants from vehicle exhaust are having far more of an effect than GHG do or ever will.
Speaking of cities, heat, models, climate change and mitigation:
What I find interesting is that they dismiss the models that produce output that most closely matches the tropical troposphere as having temperature increases that are “unreasonably low”.
Meanwhile these “unreasonably low” outputs are also the only model outputs that come anywhere close to the temperature increases that we are actually seeing out here in the real world.
Re: #128
I see the paper and resulting discussion in a much different light than you, Beaker. There is little doubt (including the result after multipling the uncertainty limits by n^1/2) that there is a relatively low probability that the differences between the models outputs and the instrumental measurements could occur by chance at the 500 and 700 pressure heights. The uncertainties in the 22 model output and the biases from one model to another is a point that the paper opens to discussion.
I think the readers and analyzers of this paper can garner considerable information about the state of climate modeling and the GHG finger print in the tropics that goes beyond a reiteration of a possible error in omitting n^1/2.
Careful what you wish for, it looks like the team is getting ready to publish a big collab on this issue (or already has?) As I just noticed this reference made by Tom Wigley in an exchange on Detection and Attribution between Singer and him:
http://sepp.org/Archive/weekwas/2008/Jan12.htm
Jeez, how many co-authors did they need?
Steve #152 “one of the problems with IPCC is their attempt to be all-inclusive.”
And vague and elusive?
Fred Singer (via Paul Biggs) says:
A sensible procedure would be to create a mixture Gaussian model, with one component for each model. Each component is defined by the mean and variances for the runs for that model. The weights for each component would be equal reflecting no preference for one model over another. A background component for all models with only a single run might be neccessary. You could then estimate the overall mean and standard deviation from the mixture model.
However, the real problem is the use of the standard error of the mean rather than the standard deviation. A comment from Fred on this specific point would go a long way to clarifying the issue.
As the graphs in the paper show multiple plots for the observed data that do not exactly coincide, it is evident that the data are uncertain, otherwise we would get the same result from the different sources. Also as I have already pointed out, the observed data are one possible realisation of a chaotic process. If the initial conditions had been slightly different we may have different results, so there is inherent uncertainty in estimating underlying climate from the data. Also the estimate of a statistical trend from a finite data set will have inherent uncertainty on it as well.
The most serious issue is the use of the standard error of the mean instead of the standard deviation, this may not have been the first point made on RC, but it was the most important in terms of the validity of the conclusions. That is ithe issue that is most in need of comment from the authors.
The area within two standard deviations represents about 95% of the uncertainty. It would be highly odd to describe data within two standard deviations of the mean as “outliers”. So this may be a criticism of using the range, but it doesn’t apply to the standard deviation.
ouglas Hoyt says:
But aren’t these the mean outputs for each model after averaging the variation due to the stochastic noise? In other words a model can be over-predicting the trend on average, but itself have a spread of runs that are consistent with the observational data (taking into account the uncertainty in the data).
This is the problem, falsifying the models is a BIG claim, showing that there are problems with the models is a much smaller claim. Douglass et al make a claim that is not supportable by the data, IMHO, it would be best if they issued a correction, making a weaker, but justifiable claim.
RE: 144
Willis, thanks for the graph in 144. Can you clarify something for me?
Are the models you show in 144 the same as the ones RealClimate used to calculate the confidence intervals shown in the graph in comment 85?
I ask because I don’t see how that data could yield the surface values shown for the lower limit CI in graph 85.
Thanks again for a most informative graph.
I love this one:
So let me get this straight. They are saying that the reason the models don’t agree with reality is because reality is wrong? Wow. Talk about getting things completely backwards.
I like Briggs post on the problem with havng multiple models. Gavin weighed in, in a helium
sort of way.
I know what standard error of the mean is, and what standard deviation is, but why is one correct and the other not, in this case? I don’t recall seeing why (aside from the outcome of error bars that are “too wide”). Can anyone simply explain why standard deviation is the choice, and why it gives “better error bars”?
Unless of course that was the actual point of the paper.
Let me see if I can formulate the argument discussion. That 1) The paper doesn’t prove models and observations don’t match in most of the tropical troposphere, because it used the standard error of the mean instaed of the standard deviation. Versus 2) The paper proves that the range of the models makes anything possible, so it doesn’t matter what they did models.
Or as Yorick #161 said:
I can make up anything I want, and as long as I make the mathematics complicated and obtuse and confusing to hide that I made it up, my confidence interval will prove it’s impossible my wooden toothpick won’t always functions as a magnet and point North.
Something like that.
I think Nylo #160 is correct; if the standard deviation should have been used but wasn’t #1
is correct yes. But on the other hand if all you’re trying to prove is you can’t defend the models since they predict everything #2 is correct, yes.
In that you can claim in the abstract you’re trying to do one thing when in reality you’re trying to do something a little more nuanced.
164: Andrew, I just ran my code to pick out the tropical results (30N to 30S). The mean surface trend falls from 0.17 C/decade to -0.05 C/decade after filtering the contaminating effects due to surface processes and data inhomogeneities. Bear in mind that the tropics includes a lot of low-income countries with crappy data and many grid cells with too few continuous observations to identify a trend. The surface data are very sparse and the contamination effects appear to be large. On the basis of these calculations I would say the tropospheric trend likely is larger than the surface trend in the tropics, since a small positive number is larger than a small negative number.
Sam Urbinto says:
The example I gave previously is as follows:
Consider this, I can make a computer model of a six sided dice (e.g. using the random number generator in MATLAB). I can then make n ensemble of 100 model runs, and I get a mean of 3.68 with a standard error of the mean of .1601. Now I roll a real dice and get a 5. Does this invalidate my model of the dice because the observed data lies outside the error bars giving +- 2 times the standard error of the mean? No of course not! Does the value 5 lie within the spread of the ensemble? Yes it does.
basically the standard deviation describes the uncertainty in the data, i.e. the range of plausible values within the distribution, where as the standard error of the mean only measures the uncertainty in estimating the mean of the data. If we had an infinite number of models, the standard error of the mean would be zero, but that would not imply that there was no variation between the models. That alone demonstrates that the standard error of the mean is the wrong statistic.
hope this helps
Re #178
No they’re saying the attempt to measure that ‘reality’ has errors.
Rather like comparing the results from a computer code for the temperature field in a gas turbine with the measurements from an unshielded thermocouple, the ‘reality’ will be in error because the ThC will measure low. In the case of satellite measurements of tropospheric temperatures contamination from signals from the lower stratosphere will affect the measured trend.
http://en.wikipedia.org/wiki/Standard_error
Standard error of the mean
The standard error of the mean (SEM) of a sample from a population is the standard deviation of the sample (sample standard deviation ) divided by the square root of the sample size (assuming statistical independence of the values in the sample):
SE = s/n^1/2
where s is the sample standard deviation (ie the sample based estimate of the standard deviation of the population), and n is the size (number of items) of the sample.
I have a doubt (well, one of many) about how models deal with temperature and pressure data in the troposphere and their relationship with the absolute concentration or density of GH gasses. As I see it, when the temperature in the troposphere is higher is when it mostly radiates energy back to the surface, warming it. However, for the same air pressure, higher temperature means less density of the gasses, less air, which means less GH effect gasses density or concentration (in absolute terms or per unit of volume), which means less heat trapping and acts as a negative feedback: at the same time we are emitting more heat back TO the surface, we are also starting to let out more radiation FROM the surface.
The key of the process is the bolded condition I wrote above, “for the same air pressure“. My intuition says that temperature changes and pressure changes are not immediately related, because of the strong inertia of the winds. You can have high pressures both with very cold and very hot air, and one thing doesn’t immediately lead to the other. The overall implications would be that wherever surface emissions are higher, the greenhouse gasses will have opened a small window to let more of them escape. And because emissions depend on T^4, those are by far the most important places for the earth’s emissivity.
Let’s put an example. It’s August and we have the northern hemisphere of the planet clearly hotter than the southern hemisphere. Overall air pressure, on the other hand, is quite similar in both hemispheres. Even if the relative concentration of CO2 for both hemispheres is similar, the southern hemisphere is colder and has more air and therefore more CO2 than the northern hemisphere. On the other hand it is the northern hemisphere with its increased temperature the one which is emitting the most energy to the space, and with less CO2 to trap the energy. Add to this that the relative concentration of CO2 is NOT the same in both hemispheres because there are lots of plants growing and sequestering CO2 in the northern hemisphere at this time of the year. What happens? That both the relative and absolute concentrations of CO2 are weaker wherever the surface emissions are higher. It’s a clear negative feedback.
Does any of this make any sense? If it does, is this behaviour included in the models? The greenhouse effect won’t stop to exist, but its influence on the models would be reduced by implementing this simple reasoning.
That does help, but I think I understand better some other comments about why it’s not so clear cut as that. In the case of a die, there are six discrete choices and only six, where we have to get a whole number. Yes, the probability distribution over time is going to be somewhere close to the center at 3.5 One standard deviation from the mean around 70% of the time, right? Um, confidence intervals. However, I’m always going to be off by X because I can only roll a 3 or 4 around the center. (If the mean is 3.5, the error is +-.5, but our actual range per roll is 3.5 +/-2.5) But of course, each roll has a 1/6th chance of any of the spots no matter what, so each roll is 16.66% as likely. Many ways to phrase the same thing.
So I don’t see how that proves anything about 20 (or 22 or whatever) models that have variable outputs even at one altitude, much less over multiple ones, with, as Ross pointed out, spotty and/or incorrect data from observations, and how those observations actually relate to models that don’t agree totally with each other in the first place, regardless of how you combine them.
Your example is for a discrete distribution, but the problem seems to be one involving a continuous distribution that’s unbounded. Um, infinite support? I’m not saying you’re wrong (I’m not a statistician… Obviously….) I’m just wondering if perhaps the method of valuing the models, for this purpose, is more about the standard error in the mean.
I have the same question Dr. Singer had; Were (or how were) the 22 models with a total of 67 runs with 1-10 each weighted?
Perhaps neither of those methods is appropriate.
Can all the statisticians here chime in on what method would be best to aggregate these models? Like a consensus vote. It seems there’s not enough information to really know, or there’d be better agreement on this.
My #186 was for beaker’s #182 Thanks BTW, I had missed that earlier.
Kenneth #184 “assuming statistical independence of the values in the sample” Can we? Should we? Did you put up the definition because it applies, or because it doesn’t? 🙂
Nylo #185 That is one of the obvious complexities. Inertia of the wind. The vast differences in behavior NH summer with plants involved and temperature ranges higher, more urbanized, and more land, versus more water colder less plants SH. Then we get SH summer where the temps change the other way from NH but we still have less land, less urbanization and fewer plants.
Hmmmm.
Beaker, regarding 182
Beaker, your dice example in comment 182 shows the fallacy of judging a model by evaluating the standard error of the mean calculated from multiple runs versus a single data point (one throw of the dice). But that is not what Douglas et al is doing, is it?
As I understand it, they are not comparing the standard error of the means of the models to single data points out of a distribution — rather, they are comparing standard error of the mean of the models to observations which themselves are supposed to be the mean temperature trend at different altitudes.
It seems to my limited statistical knowledge that they used the correct metric. Am I wrong?
Re: The plot in #144 of Temperature versus Altitude.
Nice plot Willis.
But I notice something about the collective measurements. You describe them as ‘all decreasing’, which is fine. But they also all have a hump. If you separate the observed data into “below 500” and “above 500”, all the above 500 data basically follows right along with what the models say – qualitatively. That is, increase until somewhere around 250hPa, then drop. This same graph with the reference datum placed at 500hPa would seem much more agreeable on the right half.
But… even less agreeable on the left. This would seem to imply that the models are understating some actual ground level warming process. Processes like urban heat islands and land-use changes.
Thanks for correcting the caption to Figure 1.
Yes, the difference between NH and SH is important. A uniform increase in CO2 concentration leads to a higher percentage of absorption of the surface radiation. This means that tropospheric temperature should increase more wherever emissions were already higher, so although there is a temperature increase in both hemispheres, temperature differences between hemispheres in the troposphere should increase, especially during NH’s summer. But this at the same time leads to more air moving to the south in the summer and to the north in winter, and less mass of air and GH gasses staying wherever the emissions of the surface are high. It is a clear negative feedback. How important, I can’t say.
181 (Ross): Thanks, I figured that it would be much lower. I guess that would kinda imply that there is no overlap at all between the model output and measurements without including huge error bars. However, it would help to explain the (apparent) absence of the expected pattern somewhat.
Ah, but the clouds have a large influence also. And what influences clouds become more important to look at.
The 1999 NASA Earth Observatory article about GSFC’s work on cloud formation studied through ship tracks from sulpur emissions I linked in in my # 170 deals with NH/SH quite a bit in the last couple of pages, and might be interesting to see what they were thinking of and doing a decade ago.
It even has a funny title, every cloud has a filthy lining
Phil.
Let us suppose that you build a model modeling the response of a
vastly complex system. And let us suppose that the measure of merit we are
interesting in is temperature. A global average. So, you can get bits and pieces
right or wrong, but if we allow you mash togther all your wrong guesses into
one big final guess, then I suppose we are being fair to you. So you simulated the
phenemena at a micro temporal scale and micro time scale, and we’ll only judge you
on a multidecadal, global scale. The scale at which you are least likely to get anything
wrong.
OK. fair test. c student type test.
If the obseravtion record, which is so jealously defended, indicates that the 1930s
where a hot time, and your model totally missed it. what would you conclude?
not as a warmist.
As a thinking person.
What would you conclude. I’ll share the ModelE hindcast after you answer.
And if the model matched, could you spell beta?
No hints either way. Just a test of you, not the data.
(167) Fred
Those of us that look at pyrometers and bolometers at the surface see a dimunition of solar radiation at the surface on days with high humidity and or with high pollution values. The data from the University of Nevada Las Vegas and other NOAA locations clearly show as much as 70-90 watts per square meter decrease in solar radiation at the surface from these effects.
That is a significant number that is well documented in the solar energy industry but apparently never looked at in the climate community. (or is it?)
Regarding the Douglas statistics:
The problem is that we can’t agree how to handle the model outputs. Dealing with uncertainty in data collection is well established, and everybody learned how as an undergrad.
We didn’t learn how to deal with “model” outputs. (Except for a few grizzly engineers. These are the ones howling about a lack of engineering quality documentation for the GCMs) Model outputs look like data–especially when we “re-roll” the inputs to get a different set of outputs. But models are not data, and that’s why we can’t agree on how to use the data.
If you believe (as Douglass et al seem to) that the models outputs are drawn from a normal distribution about some “true” curve, then the “Standard error of the mean” is correct, and you could drive uncertainty towards zero with a large enough set of models. People who believe this want to use ensembles.
If you believe that the model may have fundamental problems (as Beaker seems to) than you need to estimate uncertainty of each models assumptions, propagate that through the model, and calculate a final confidence distribution. Beaker seems to call this “standard deviation”, but I think that it’s better just to call it uncertainty, since the model is not guaranteed to propagate Gaussian inputs into Gaussian outputs. When combining these models, you MUST combine the uncertainties correctly, or you have lost all predictive power. This seems to be Beaker’s point. People who believe this would rather have one good model, than a hundred mediocre ones.
Which is right? I don’t know. Some combination I suppose. The IPCC seems to lean towards the Douglass interpretation–or else why would the pursue to so many different models?
Beaker, do you think this is a fair interpretation of the disagreement?
I wish I could “improve” my checkbook balance in the same way these guys “improve observational records.” However, we can wait and see.
erik #196
It certainly seems that this might actually be a question of how you think about the models rather than a statistical issue. I think that’s what Ross was saying when he said forget statistics. It might be the method you prefer (or believe correct) is determined by if you prefer using one or many, and how you think either is best served.
Or even more still, what I said in #186 about the models versus observations and Michael commented on in #188 What are the models telling us and what the observations are telling us. Or in other words, what are we comparing? The same thing?
I started asking questions because I pretty much understood the points, but not the purpose. The what and not the why. Seems it’s a typical climate discussion; both sides think about the same thing from a different outlook. They think they’re discussing the same subject. But they’re not. So no agreement, discussion goes in a circle.
How about it beaker?
Allan #189: “But… even less agreeable on the left. This would seem to imply that the models are understating some actual ground level warming process. Processes like urban heat islands and land-use changes.”
I totally agree.
#181 Isn’t that the beautiful irony in the argument about the near surface:LT data – if the non-climatic warm bias is removed from the near surface data, then the LT becomes warmer relative to the surface – greenhouse warming as described in models is validated, but the surface warming becomes much less alarming and there is no ‘big warming’ via CO2.
199: Yup. When the dust settles I would not be surprised if this is the picture that emerges. Amplified warming aloft in the context of very low overall GHG sensitivity. Everybody gets half a loaf.
Re: #196
Erik, I agree with your view of the “standard deviation” versus standard error argument as expressed in your post – and it also gives me pause to why Beaker thinks it should be a choice between “standard deviation” and standard error.
Re: #199
Couldn’t much of these complications be handled by comparing the observed and modeled ratios/b> of troposphereic to surface temperature trends.
199, 200: How would you explain glacial-interglacial swings with a sensitivity significantly lower than ~3C?
Different “trajectories” produced by a chaotic system are not stochastic.
erik (and beaker and everyone who replied), thanks for your answers and comments. erik, you say:
It is not just Douglass who thinks the model outputs are drawn from some quasi-normal distribution about the actual observational data. It is a central claim in the IPCC, as shown by their use of “ensembles” of models.
However, in this case, it is clear that the model outputs form a quasi-normal distribution but not about the actual observational data.
Here’s a thought experiment that might shed some light on why it is not correct to use the range.
A hundred models have been run. The results of the model runs are being released one by one. Every single one of them is higher than the data. A total of ninety-nine models is announced, every one much higher than observations. The modelers are looking glum.
But wait! The hundredth model, the one where the programmers didn’t quite catch all the bugs, gives a different answer! It is below the data. The modelers cheer wildly, the data is now within the range of the model results, the world catches its breath in relief …
beaker, perhaps you could comment on this scenario.
Also, beaker, you say:
What you are saying here is that the models are “throwing dice”, and that the observations are also “throwing dice”. But that’s not the situation. We are not trying to see if the dice are the same as some other dice. We are trying to find out if the dice are loaded, whether they (on average) read high or low.
Now, a true six-sided die will (as you point out) have an average of 3.5. Suppose we come up with an average value after throwing a thousand dice of 4.5±.05. I say “the answer should be 3.5, the dice are loaded”.
You say “No, your answer of 3.5 is within the range of possible dice throws, so the dice can’t be loaded”.
We are not trying to determine if the model range encompasses the observations. We are trying to decide if the models are loaded, that is, if on average they read higher or lower than the observations.
w.
Kenneth, you say:
Ratios get tricky very fast. Suppose the surface trend in my model is zero, and the trend at 900 hPa is +0.1°C/decade.
What is the ration of tropospheric to surface trend in this case?
w.
Willis,
Another way to phrase it. If you run two models, one that produces a Venus like Earth, the other producing a Mars like Earth, than no matter what the data says, you can argue that you are always right because your models encompass the data.
#202 – I wouldn’t explain climate as being driven by CO2 – CO2 follows temperature, not the other way round. Granted adding man-made CO2 will, all things being equal, cause some warming, but the greenhouse effect is pretty much all done by 300ppmv. Climate sensitivity to CO2 is low (around 1C for the iconic doubling) IMHO, if anyone can prove me wrong, be my guest.
Willis,
I don’t think just an average will tell you if the dice aren’t true. A single throw won’t tell you anything because there aren’t enough degrees of freedom in the experiment. You need a lot of throws and you need to look at the distribution across each face. If you load the dice on opposite sides, the average will still be 3.5, but the dice won’t be at all true. You will have a lot of ones and sixes, say, and fewer of the rest of the faces.
As I said in 188, I don’t think Beaker’s dice example is analogous to the comparison being done in Douglas et al.
To re-state, Beaker’s example with the dice is only analogous to Douglas if the different observations the models are being compared to in Douglas are viewed as individual data points — individual data points that don’t necessarily represent the true mean, and may be as different from the true mean as any one throw of a dice may be different from the mean of a hundred throws.
But surely this is not true of the observations in question. The satellite and balloon observations are not single data points out of a larger distribution — not in the way, for instance, that the Atlanta surface temperature observation is only a single data point that cannot be counted on to represent the true mean surface temperature. Are they?
It seems to me that Douglas et al is actually comparing two things that both purport to represent reality: The mean of the models and the best measurements we have of actual temperatures. Given that comparison, isn’t the standard error of mean the best basis for comparison?
#207
But Paul, what about the MODELS. Don’t they count as proof???
/sarc off
That would be okay–if you properly accounted for all uncertainties. Assuming you did this correctly, The uncertainties on the two models would have to overlap. (If the didn’t overlap, you would know that at least one of them was wrong.)
Lets say that the mars/Earth model predicted temp = 213K +/- 100K.
The Venus/Earth model predicted temp = 738K +/- 500K
We could combine the uncertainties in these models, and know that the true Earth temperature would have to be between 238K (738 minus 500) and 313K (213 plus 100).
By combining the models, we can actually reduce the uncertainty. But only if the uncertainties were correctly calculated for the original models. Unfortunately, that calculation seems to have never been published. It may not even be possible. (Although the discrepancy between models does put a lower bound on the uncertainty.)
205 (Willis Eschenbach): I “hate” to be pedantic, but a trend is almost never exactly zero. 😉
207 (Paul Biggs): I could argue for lower, but I’m not sure how good I’d be at defending such an estimate.
All this talk of error bars, uncertainty, etc. is making my head spin. Can someone quickly summarize the points we can agree on? I think that we can agree that the models and observations don’t “match” but that this might be because we need to account for model uncertainty and measurement error, correct?
Well, yes Andrew – 1C might be generous!
There are two problems:
1) Of what use is the uncertainty of an ensemble of models in the first place? Are they all, in some sense, randomly distributed around a core set of assumptions that we can hope to evaluate by treating them as though they were observations drawn from a single distribution? If so, then we can use the standard error of the mean corrected for the inherent variability between model runs within each model – which we don’t know, of course, but if we did, we might plausibly construct a test to reject those core assumptions by rejecting the models as an ensemble. I’m not sure the assumption of a core set of assumptions holds, however. If not, we’d need to reject them one at a time.
2) But in either case, we’ll have a difficult time, because the models are simplifications. Their creators will (presumably, and assuming that they don’t simply find a more suitable set of measurements against which to compare their models) say that they model a trend away from which natural variation (of cyclical nature but unknown and unspecified amplitude and duration) will occur, but to which the climate will ultimately return (at all altitudes, of course!). Rejecting a model like that is not just more difficult because of the decreased accuracy over time frames ranging from 0 to whatever, but because you need to know the true extent of that natural variation – not just the variation in the model runs.
Does anyone know the extent of natural (unmodelled) variation? If not, then nothing can be rejected, because we don’t have any way of estimating this variability.
Which is why I cringe when someone fits a linear trend to a temperature record, and says “we’ve been warming (cooling) at…per decade (p
With all this talk of which particular type of error measurement is appropriate for a sample of different models, has anyone even checked if the output of the models forms a normal statistical distribution both in the results of their runs, and the collection of their means ? Otherwise arguing over whether its standard deviation or standard error of the mean is a bit beside the point.
The IPCC constantly uses ensembles of model behaviors based on the assumption that this is the
best guess as to what the science says at the moment (the failures of any model canceled out by the
other models). This is not an implausible position to take. The mean of these model runs represents
the ensemble behavior and the confidence intervals on that estimate are as Douglass et al calculated.
Also note that no single model comes close to the observations either. I like Ross’ summation way up
above: if you claim a variance so large that it encompasses all behaviors, then what scientific
test would disprove your theory? Or: a theory with no statistical power is a theory without precision.
anonymous, you ask:
Can’t help with the individual runs, don’t have the data. The means dataset is too small (22 models) for any of the normality tests to be of use (Kolmogorov-Smirnov normality test, Shapiro-Wilk’s test for normality, Jarque–Bera test for normality, D’Agostino normality test). However, all is not lost. Here are the violinplots for each of the levels from the surface upwards:
I have included a normal distribution of 22 data points as the first violinplot, for comparison of the shape with the surface violinplot.
However, you have to remember that the number of datapoints N is very small, only 22, so we would expect to have a large variation in shape for the violinplots.
DeWitt, you say:
As Winston Churchill once famously said, after being accused of ending a sentence with a proposition, “This is pedantry up with which I will not put”.
Among other things, I said the result was “4.5 ± .05”, so your example of a die equally loaded on opposite faces is simply not possible because as you point out, the average will still be 3.5 … but I already specified that it wasn’t 3.5. Also, it is immaterial whether taking the average will find all kinds of possible loadings (it won’t). If the average is not 3.5 (± error), we know the die is loaded.
You understand the point of the thought experiment, I hope. If we want to determine if the die is loaded, we can’t say “the observational result of the testing (average of 4.5 ± .05 in my example) is within the range of individual throws of the die (between 1 and 6), so the dice must not be loaded.” That’s the interpretation that beaker is arguing for, that the observations kinda sorta fall within the range of the models so the models are not giving erroneous results … doesn’t work that way.
w.
#216, Craig
Actually it is. Multiple models that disagree among themselves and with the data is the definition of ignorance. Averaging ignorance doesn’t produce knowledge. The precise form of averaging is meaningless when the underlying science is clearly wrong.
The only way to proceed is to take the two models that sorta-kinda agree with the data and compare their predictions to other independent measurements. If they still agree then maybe the scientists who built them actually know something and the climate modelers can learn something from them.
From all this it seems reasonable to suppose that if a model, or class of model, existed that could reliably reproduce
a) observed surface warming
b) observed tropical troposhpheric warming
c) catastrophic future surface warming
we would have heard a great deal about it by now. The upcoming attempt by Santer and his batallion to rewrite the observational data is in effect an admission that there is no such model, and that a serous problem exists.
Wondering, Steve, whether you, as the resident statistics expert, can help out here and settle the argument going on here between Beaker and Willis, Douglass and RC.
215: Good point. There has been a lot of talk as if realizations of a chaotic process are Gaussian. That is certainly not a safe assumption, in fact chaotic processes needn’t be stochastic at all. If they do contain stochastic processes, they might be Levy or some other fat-tailed distribution. At the outer limit, as was mentioned above, we could just resort to Chebychev’s inequality, implying very fat tails. Presumably this would make the RC argument even more vividly, replacing Douglass et al. narrow confidence interval for the mean of the GCM runs with as wide a span of outputs as you can fit on the page. And where would that leave us? Sure, you avoid having to concede the models are rejected, but only by arguing that they are vacuous.
Willis, #204: When you say “the range” do you mean within 1 sigma of standard deviation to see if they all are between 3 and 4 on the die? Or, I mean, the models are somewhere in between some number of sigma or less compared to reality, or the models to each other, or? Also, is violin the same as candlestick but able to make beautiful music? 🙂
Die analogy
There are two things there. First, if we get 4.5 +/- .05 or 2.2 +/- .8 in millions of throws, we know the die is loaded. If we get 3.5 +/-.5 we don’t know if it’s not loaded.
Now, if we know it’s biased out of random, we know know it’s biased out of random. How exactly? Do we care? Throw it away. 🙂
If we don’t know if it’s loaded or not, now we have to look at the frequency of the numbers, correct? That would tell us if that 3 to 4 mean favors some number(s) rather than others (the real law of large numbers analogy would be that each number came up 16.67% of the time, wouldn’t it?).
So your initial data determines the next course of action, unless you just wanted to see what the distribution of 1 2 3 4 5 6 is
On the other hand, as I said; is a 3D system simulated by various numbers of various simulation runs in various ways anything like a range of 6 discrete numbers?
Dice would be two sets of six or more, perhaps more valid as an analogy. 🙂 What does the σ2 look like for a random number of die with random numbers of sides when thrown with different random variables each time? As a matter of fact, what does the median, mean and mode of that look like?
If we put 15 cherries together with 7 apples, can we still make pie with a variance of 16 and a standard deviation of 4?
#202 – Jon, your question implies that there is a settled view to the effect that [existence of ice ages] implies [2xCO2 sensitivity at least 3C]. I doubt this view is actually held, and if it actually were true I think the IPCC would have splashed it around by now. If you know of some papers, cite a few and we can chew them over. Even the IPCC uses a range of sensitivity values of 1.5 to 4.5 C. And they don’t seem to deny the existence of glaciations and deglaciations. I do not know what, if anything, is the standard explanation for deglaciations, but I am unaware of any reason to believe it is inconsistent with low sensitivity to CO2. But that’s just mho.
202 (Jon):
There was a recent paper on this:
http://www.agu.org/pubs/crossref/2008/2007GL032759.shtml
Also, see this exchange between Lindzen and Hoffert and Covey:
Click to access 165pal~1.pdf
And this:
Now make up your own mind.
AGH! My post keep being eaten by the spam filter for having to many links.
202 (Jon): Please see the thread on the bulletin board:
http://www.climateaudit.org/phpBB3/viewtopic.php?f=4&t=128
And not the various studies linked there (including one directly dealing with your question).
Ross M, thanks for your thoughts. you discuss chaotic processes above. However, it is worth noting that the models are not chaotic in any sense. In fact, their outputs can be replicated (without the noise) by a much simpler model, as is done by the IPCC. Which of course raises the question of why we use complex models when simple models can replicate them … but I digress.
w.
Re 140 Yorick
About 2 months ago someone (maybe Judith Curry) said that fewer than half the modellers now used “Flux Adjustment”. CSIRO say they do not.
Re # 167 Paul Biggs
This Singer quote is relevant-
22 models with 67 runs are reported for the Douglass et al paper. What we know not is the number of runs done, but not reported by the modellers, who, being human, would be inclined to report their “best ones” and those “closest” to the others (I suppose that there is a fair deal of exchange between modellers before they go to print). So, is there much point in endless argument about the error derivation on the models presented when there could be a large number unreported, which could affect the error even more if included?
What is more, the models themselves mprobably use smaller bundles of numbers each with their own uncertainties and error distributions and stats, yet report them as a single number. (I’ve been lectured on RC about the central Limit theory, which I first encountered personally in 1970 or so).
On a first slow read of Douglass et al I did not feel that the numbers were free of scribal or other unstated errors so I wrote to CSIRO (model 15) and to Fred Singer and to CA and to RC. Answers are still coming in. Some are not very enlightening. Quality shows.
On deeper thinking, I suggest that the methods used to calculate errors are of little consequence. This is because nobody knows the correct answer in nature. While more work might bring model agreement closer together, this is like the old argument about improving “precision” while not being able to say much about “accuracy”.
Is there a master plan for modellers to follow or do we have clusters of researchers poking at data to see what falls out? Repeat – where are the criteria that should call a stop if the future is shown intractible? (I’m used to working in an environment where good results are a prerequisite to more funding after recurrent 6-montly review).
R #194
I’m not sure what brought this on?
That either the model or the data were at fault.
I don’t see the dichotomy you suggest.
Actually for a fairly long time I ran a lab which did 3D 2 phase flow modelling and state of the art experimental measurements. We learned a lot by carefully comparing the results of both, sometimes the models were at fault sometimes the measurements, whenever there was a mismatch we made no assumptions about which was right but carefully assessed each.
A non-negligible proportion of the climateprediction.net models were rejected as not making any sense, e.g. for developing a “cold equator”. See discussion here with one of the runs showing the development of -3 deg C offshore Ecuador. So there’s obviously a sort of pre-screening before a model is reported.
More evidence of this is in the Kiehl results where he found a high correlation between model sensitivity and aerosol history. Since climate science has no policy requiring disclosure of all cases, one is left to speculate as to how this tuning came about.
Isn’t that what I said?
Michael Smith says:
Yes, it is exactly what Douglass et al. are doing. The observed data is “one roll of a die” in the sense it is one realisation of a chaotic system, whereas the model runs are multiple realisations. The question that we would really like to know is “is the physics embodied by the models a close match to the physics giving rise to the observed data?”. Unfortunately we can’t address this question directly as we only have one realisation of the observed climate, so we can’t average out the “multi-decadal weather” that Steve mentioned. The best we can do is to see if the observed data could have been generated from the models with reasonable probabliity, which is what a comparison with the standard deviation achieves.
That is what they are doing, however what they did doesn’t support their conclusions. Had they concluded that the models are biased (i.e. on average they over-predict), that would have been O.K., but this is not the same thing as saying “these models could not give rise to the observed data”, which is what would be required for the observed data to invalidate the models. The test they did is O.K. (ish), it just doesn’t answer the question they claim it does.
Hope this helps.
#223 – AR4 modelled scenarios for climate sensitivity to doubled CO2 range from 1.1C to 6.4C iirc. The assumption is that most feedbacks are positive, which may not be correct, and Roy Spencer has some interesting publications on large negative feedback – one published, one in press.
erik says:
It is actually pretty simple. If you have a variable of interest (say crop yeld), you make a model that relates temperature data into crop yield. You then run the output of each GCM run separately through the crop yield model and store the output. What you have then is a distribution over crop yield that takes into account the uncertainty in the GCM as you have propogated this uncertainty through the crop yield model. The more GCM runs, the better. The mistake is to try and find one true value from the GCMs, the whole ensemble should be used in making predictions.
As a grizzly engineer myself, the main problem seems to be that too few in this field are happy with reasoning based on uncertain information. The maths for doing this is fairly well sorted out, but it seems rarely used in practice. It seems odd to me that e.g. IPCC reports seem to have so few professional statisticians among the authors when there are so many statistical issues.
No, that is not correct. For the data to falsify the models, you would need to show that the models were not capable of generating the observed data. For this, you need to show that the observed data fall outside the bulk of the distribution of the data. The standard error of the mean doesn’t tell you that as the uncertainty in the model outputs does not decrease as you add more model runs, only the uncertainty in your knowledge of the mean.
The standard deviation provides an indication of the spread of the data for any distribution, not only the Gaussian, however my main point is that you should not ignore the uncertainty in making predictions, but instead should follow standard Bayesian procedure and marginalise over it in making predictions.
I think this is confusing two issues. If you are going to use a model ensemble to make predictions, and you are not willing to marginalise, then using the model means is the next best thing to do (or at least a reasonable thing to do). However, this does not mean that you can falsify the models by looking only at the ensemble mean, the variation within the ensemble is also important, and this is where Douglass et al. go wrong.
hope this helps
Kenneth Fritsch says:
Simple, Douglass et al. make a specific statistical claim. The statistic they used cannot be used to justify that claim as it measures the wrong thing. If you use the correct statistic and re-run the analysis, the claim is not upheld. If you are going to use statistical methods to establish a point, you have to get the methodology right, especially in a high-profile paper such as this which has recieved a fair amount of media attention.
The choice is: Do I wan’t to find out if there is a statistically significant bias in the models or do I want to see if the data falsify the models? You use the standard error of the mean to answer the first part and the standard deviation to answer the second.
Ross McKitrick says:
It was Douglass et al. that chose a Gaussian approximation to the distribution (I think I have discussed this previously). If you accept this assumption then the standard deviation is the correct statistic, not that standard error of the mean, that is the key issue. Of course they should have tested their distributional assumptions, but that is a secondary issue, I would be surprised if the skew or kurtosis of the actual distribution were sufficient to make a four fold difference in the breadth of the error bars in the way that substituting the standard error of the mean for the standard deviation does.
Personally I would go for some form of non-parametric density estimation and avoid distributional assumptions entirely.
As I have said, all you need to do is use the ensemble in a Baysian mannr (by averaging over models) and you have a way of making predictions that takes model uncertainty into account. Then see if the predictions are reasonable.
234 (beaker): I can see why the different runs of the same model would create a probability distribution which must be used to determine whether that particular model has merit. However, I don’t see how one can justify treating multiple runs from different models to create a combined probability distribution. This sets the bar so high because it implies that all models must be treated as correct if even a single model manages to produce a single run that is comparable to the actual temperatures.
I think it would make more sense to evaluate each model seperately accept/reject them based on a ensemble containing only its runs. If any models overlap the actual temps then they could be combined into a new ensemble that can be used for further analysis.
Raven says:
It is not a matter of “setting the bar”, it is a matter of choosing the correct statistic to test the hypothesis in which we are interested.
There are two forms of uncertainty in the models, the stochastic element and a systematic element. Using different models expresses the systematic uncertainties, which are also relevant in deciding whether GCMs as an approach are falsified by the observed data. If you test the models separately, then you can’t make a general comment about GCMs as an approach, only the validity of specific models.
There is also the point that the observed data don’t give you ground truth about the underlying climate, only an estimate based on one realisation of a chaotic process. If we had multiple parallel Earths with the same climate forcings but slightly different initial conditions, we would expect to see a range of different observed trends on each of them. There is no guarantee that the trend observed on this particular Earth is not in the lower tail of that distribution (and we have no way of really knowing how broad this distribution is).
I know this is going to attract more comments along the lines of “beaker is saying the models are right and the reality is wrong”, however this is not the case, the observed data gives an uncertain indicator of the underlying climate and that uncertainty should not be ignored.
beaker says:
I don’t think we care whether GCMs are a useful approach or not. What we care about is the validity of the specific GCMs that are being used to justify policy decisions. For that reason a sub-set of models with distributions that overlap reality is more interesting than the entire ensemble.
We also need to identify other metrics such as surface temperature which can be further used to refine the set of validated models that are used for further analysis. If we cannot find a single model with a distribution that overlaps reality for different metrics then we can assume that none of the GCMs provide any useful insight into the future of climate.
Beaker, thanks for responding to my comment. You say in 232:
This is from the summary of Dougalas et al:
It sounds to me they concluded pretty much what you said: that the models “over-predict”.
You also say, in 238:
But that one “realisation” has been inconsistent with the models since 1979. What is the likelihood that our one “realisation” would be consistently biased for 28+ years?
And finally, in using the standard deviation to demonstrate that Douglass et al does not prove that the models cannot match the observations, doesn’t that amount to saying that the models might, given enough runs, show no or little AGW?
Flux adjustments still exist in many of the models, I believe. To me, this is like doing a statistical study on a set of dice throws where you have manually placed the dice to “seem” random.
beaker, you say:
No.
Using different models does not express “systematic uncertainties”. It expresses shared assumptions of the modelers. These shared assumptions obviously include the assumptions that lead to the shared prediction (and its expression in the models) that greenhouse warming will lead to increased warming trends with altitude in the tropical troposphere.
That’s the prediction, increasing from the surface upwards. And twenty-one of the twenty-two models do just that, which clearly establishes the shared assumption.
In the event, however, four separate observational datasets show cooling from the surface upwards. Not warming with elevation like in the models. Not warming with elevation like in the predictions. Cooling.
Are you seriously arguing that because one rogue model broke ranks and went south we should ignore the facts?
The AGW theoretical calculations predict increasing WARMING trends with altitude. It is central to the explanation of how the greenhouse works.
The AGW based models (21 out of 22) forecast increasing WARMING trends with altitude.
The four observational datasets show increasing COOLING trends with altitude.
If you think you can cover that up with statistics … nice try.
w.
Michael Smith says:
In asking if the models can be reconciled with the observational data they are asking whether the observed data is plausible given the models. If the observed data lies within the spread of the models then it is plausible. It maybe that they intended to show that the models over predict on average, but that is not the claim made when they say that the observational data cannot be reconciled with the data. Bias and inconsistency have specific statistical meanings that are being confused in the discussion of this paper.
Again, if you want to use the term “inconsistent” in a statistical sense, you need to ask whether the data is within the spread of the models, not is the data close to the mean of the models. I think half of the problem may be the misuse of statistical terminology. As far as I can see the data are not inconsistent with the models, but the models do over-predict the observed data. However, this could happen even if the models had the underlying physics exactly right, as we only have one realisation of the observed data. If we were on one of the parallel Earths I mentioned, with slightly different intial conditions, the observed trend might be closer to the mean of the ensemble, but we have no way of knowing that. That is why showing the models are inconsistent with the data is a much bigger claim that showing the models exhibit a significant bias relative to the observed data.
They do already (although with relatively low probability). However it is just as wrong to focus on the lower tail of the distribution of modelled trends and ignore the upper tail as it is to concentrate only on the upper tail and ignore the lower. Looking only at the mean and ignoring the variability is only a little better. A fully Baysian approach considers all plausible values for the trend, weighted by their plausibility (as indicated by the spread of models forming the ensemble).
Willis Eschenbach says:
It is this sort of comment that makes progress in discussion of technical issues on blogs needlessly difficult. I have no stance on the validity of the models to defend. I am merely pointing out that one particular paper is fundamentally flawed due to errors in the statistical methodology. I am not trying to cover up anything with statistics and it is disingenuous to suggest that I am. If anything I am drawing attention to the uncertainties involved, and arguing that they should not be neglected.
The use of different models reflects the uncertainty within “shared assumptions of the modelers”. If there were no uncertainty about the underlying physics, the models would all give a similar spread of results, but they don’t. This is the systematic uncertainty.
yorick says:
More trouble for GCMs and temperature trends – in the Antarctic this time. From Pileke Sr’s Climate Science:
Monaghan, A. J., D. H. Bromwich, and D. P. Schneider (2008), Twentieth century Antarctic air temperature and snowfall simulations by IPCC climate models, Geophys. Res. Lett., 35, L07502, doi:10.1029/2007GL032630.
The abstract reads
”We compare new observationally-based data sets of Antarctic near-surface air temperature and snowfall accumulation with 20th century simulations from global climate models (GCMs) that support the Intergovernmental Panel on Climate Change Fourth Assessment Report. Annual Antarctic snowfall accumulation trends in the GCMs agree with observations during 1960–1999, and the sensitivity of snowfall accumulation to near-surface air temperature fluctuations is approximately the same as observed, about 5% K−1. Thus if Antarctic temperatures rise as projected, snowfall increases may partially offset ice sheet mass loss by mitigating an additional 1 mm y−1of global sea level rise by 2100. However, 20th century (1880–1999) annual Antarctic near-surface air temperature trends in the GCMs are about 2.5-to-5 times larger-than-observed, possibly due to the radiative impact of unrealistic increases in water vapor. Resolving the relative contributions of dynamic and radiative forcing on Antarctic temperature variability in GCMs will lead to more robust 21st century projections.”
Pielke Sr:
“This paper provides further evidence that the multi-decadal global climate models are significantly overstating the water vapor input into the atmosphere, and thus are not providing quantitatively realistic estimates of how the climate system responds to the increase in atmospheric well mixed greenhouse gases in terms of the water vapor feedback. This water vapor feedback is required in order to achieve the amount of warming from radiative forcing projected in the 2007 IPCC report.”
Beaker, thanks, again, for responding.
I think we have two fundamental disagreements (or perhaps a failure to understand on my part).
Douglas et al defends the use of the standard error of the mean as follows:
(Italics in original)
Is it not accurate to say that using the standard deviation to calculate the spread of the models has exactly the effect noted by the end of this passage? Namely, that the standard deviation allows the outliers — which are models that are predicting essentially no significant AGW — to spread the data so wide as to permit it to overlap the observations?
That may be statistically valid, but is it logical? Does it make sense to require that a test of the validity of AGW models include models that don’t show any significant AGW?
That just doesn’t make sense to me. The Douglas et al approach does make sense to me.
The other area of disagreement — or lack of understanding on my part — involves the comments about outcomes on an alternative earth. Are you saying those outcomes are in fact a possibility on this earth, given sufficient time? That the last 28+ years of troposphere observations are an aberration?
Thanks again for responding to a layman’s questions.
Michael Smith says:
No problem, it is a pleasure to have a gentlemanly discussion of science (particularly statistics, which I find fascinating, yes I realise that probably sounds rather sad!).
I think the major problem is one of statistical terminology. In a scientific paper, it is vital that the correct terminology is used to that the conclusions are stated unambiguously. Unfortunately the Douglass et al. paper uses terms to describe a statistical test that have specific connotations in statistics that are not supportable by the test actually performed. Had I refereed the paper, I would have insisted that the claim be downgraded appropriately, it is a shame this wasn’t done. The problem is that when these findings are reported in the media, the claims are made in the strongest possible terms and so the public are mislead. As I say, “reconcile” and “inconsistency” should be used in relation to a test of whether the data are plausible according to the models, not whether the models consider the observed data to be probable. The difference between “inconsistent” and “bias” is the difference between “possible” and “probable”, the standard deviation is used to argue about possibility and the standard error of the mean to establish that something is probable.
Yes, and so they should! If there are models that show little or no warming, that should not be ignored, as it means that the possibility of there being little or no warming is consistent with the models, if perhaps rather less probable than moderate warming. Again it is the distinction between “plausible/possible” and “probable”.
It depends on the question you want to ask. The problem with the Douglas et al. paper is not so much that the test they did was incorrect than that it doesn’t support the conclusion that they draw. Saying that the models are inconsistent with the observed data is an indication of a major flaw in the GCMs (it would suggest that the underlying physics is fundamentally wrong). Saying that the models have a bias (on average they over-predict) is a much lesser claim, and one that would not be a surprise to the modellers. IIRC the paper by Santer that is mentioned in Douglass et al. draws that conclusion.
It is a bit like rolling dice, the number you get depends on the initial conditions (i.e. the exact position, velocity and acceleration of your hand etc.). Even though the dice behave in a completely deterministic manner, you can’t predict what number you will get because you can’t measure the initial conditions accurately enough. The climate is also a chaotic system, if you could roll back time 28+ years, make a small alteration and fast forward again, you would probably get a different trend. Both answers are right, neither is an abberation, it is just that there is inherent uncertainty in chaotic systems. It may be that the observed data we have corresponds to rolling a dice and getting a one or a six (i.e. an extreme value) or rolling a dice and getting a three or a four (i.e. something close to the average), however we have no way of knowing which. This is why to test whether the models are consistent with the data, we have to use the spread of the model runs to determine what is plausible.
Hope this helps
RE:141 beaker
You say:
No. The claim that Douglas et al claim falsification, is pure Gavin spin. No where in the paper do they claim falsification. The claims they make are in the paper’s summary:
Cliff
It seems that we know too much, and we know too little, all at the same time. Taking a statistical look at our knowledge, we fall into the error of believing that we have some true grasp of knowledge, when actually the error bars on our knowledge are greater than the knowledge itself.
Those whom the gods would destroy, they first drive to make statistical analyses . . . and then to believe their analyses are pertinent to the problem.
It is a shame that scientists and engineers are always required to have an answer for everything. Nobody is ever allowed to just say “I don’t know why that happens” any more. Instead of trying to do statistical analysis on collections of sparse data, we should be creating good standards for collecting data over the next hundred years, so some decent analysis can be done some time in the future. Weather stations were never intended to provide precise and accurate weather data for use in determining long-term climate changes. They were intended to provide adequate local weather data for the use of farmers, ranchers, and aviation.
beaker, Wegman made very similar observations about the lack of statistical expertise in climate science, even though so many of the problems are statistical rather than physical. Obviously one of the reasons for the popularity of the site is that there are many scientists and professionals in other fields with statistical expertise that, as citizens, are interested in climate issues and appreciate the efforts made here to frame issues in statistical terms.
I chatted with von Storch in 2006 about why so few statisticians were involved in climate science. He said that he’d tried to get statisticians involved form time to time, but they hadn’t been very helpful. His complaint – and I’ trying to represent it correctly – was that their methods tended to be much too oriented
to i.i.d. gaussian processes and that they tended not to be very helpful.
One advantage that Ross and I had is that we come at the problems more from a business/economics perspective where the methodologies are much more oriented to time series, to autocorrelation and to the problems of spurious regression, which is the battleground issue in the proxy reconstructions. One of the big troubles in the proxy debate is that the protagonists on the other side really don’t confront this issue. The reasoning on “significance” in (say) Juckes et al 2007 has been obsolete in economics since Yule 1926. It’s hard to even get to a point of sensible engagement.
There are a lot of specialist articles on econometrics and I anticipate that the quality of statistical analysis in climate science will improve over time given the publicity that the field has, though the “Team” in the narrowest sense seems uninterested. There has been remarkably little visible effort to understand the proxy issues; I think that there may be some movement behind the scenes, but an unwillingness to express this formally for fear of undermining policy initiatives that they believe justified on other grounds.
An intriguing thread full of interest and wonder!
Beaker # 245
AR4 (p591) says most AOGCMs no longer use flux adjustments, which were previously required to maintain a stable climate. So that’s clear then.
Except it goes on to say “The uncertainty associated with the use of flux adjustments HAS THEREFORE DECREASED, although biases and long-term trends remain in AOGCM control simulations.” Which seems to imply that flux adjustment uncertainties remain. Or am I reading this wrong?
Steve: As it happens my experience of working with scientists from a variety of fields generally is that they tend to be more i.i.d. Gaussian than I am when it comes to statistics and it has been difficult to get them to accept more modern Bayesian means of handling uncertainty. It is also a shame to see such scepticism about the use of statistics when it lies at the heart of quantitative science, with better statistics there would fewer strong (and unsupportable) claims made by both “camps” (not that there should be more than one!).
I tried a simple experiment to line up RSS and UAH tropics data. RSS appears to be rotated counter-clockwise relative to UAH, so I un-rotated it 3 degrees and got a nice visual fit.
I’ve read over this thread and have to say I am rather surprised by the methodology apparently used for the model validation tests. In every test I have encountered in my career (with some experience in numerical modeling of systems), an individual model is tested by running it numerous times with random inputs (Monte-Carlo runs), and a statistical analysis is then performed across the multiple runs of that model. If the observations fall outside the selected error range, it can be established to a particular confidence level that that particular model has been invalidated. Here it appears that a few runs of different models are considered in bulk, and if the observations fall within the “error bars” found by analyzing across the different models then it is claimed that none of the models have been invalidated. Is that correct? That appears to be methodologically flawed, to say the least. It is true that none of the models have been invalidated, but that is because none of them have been legitimately tested. I quoted “error bars” because they are essentially meaningless when averaging across different models. A different model will give a different statistical distribution, by definition.
Has there been a rigorous examination, subjected to peer review and further analysis in the literature, of lumping the output of different numerical models into the same statistical pool and drawing conclusions from it? I’m willing to be shown that I am wrong, but frankly, these comparisons look questionable at best.
250 (Cliff Huston): If so, then Singer has been misrepresenting their findings, since he has claim they falsified the models several times. But he coauthored the paper, so why didn’t he advance the claim in the paper?
254 (beaker): On the contrary, not only are there more than two “camps” this is quite preferable to everyone agreeing. If everyone agrees, then they will never question each other’s assertions, never test them, and never do any science, and things would get nowhere. But this is philosophy of science do you are welcome to disagree strongly.
255 (Eggplant fan): The models can’t have random input becuase we are dealing with historically know variables (with the exception of forcing by aerosols).
Cliff Huston says:
Look at the summary you posted, when the use the words “reconcile”, and “inconsistent”, falsification of the models is exactly what they are takling about. That is what those terms refer to in a statistical context.
#254–welcome to “climate science” procedures and methodologies
256 (Andrew) If there are no random inputs then every run of the model would have to give exactly the same results for the same forcings, which earlier posts say is not the case. I thought that the random inputs were things like El Ninos/La Ninas, volcanoes, etc. And in any event, that still wouldn’t legitimize averaging across different models. The real world observations obviously has randomness. Accounting for that through the imperfections of the different models is not scientifically sound.
Andew said:
What I mean was that there should be one camp, scientists interested in determining the truth of the matter, who will discuss each new finding on its merits without belonging to one faction or another, or pre-judging the right conclusions. That doens’t mean there should be agreement.
Following up my own 259, on second consideration, I guess I am confusing model-based future predictions with the comparison with current observations. My bad. (Bet I am corrected before I can even get this posted myself.) But I will stand by my point that it still doesn’t legitimize averaging across imperfect models to account for the random component in the real system (unless corrected, of course).
260 (Eggplant fan): Ah, no, if the inputs are the same, the outputs can differ, for two reasons. The first is that not all models have the same characteristics (you thought we understood how this work with all the relevant parameters worked out? Ha!) And El Ninos are not “input” the model generates its own El Ninos (sometimes) and volcanoes happened when they did so they can’t be put it randomly anyway. The second reason the model results can differ is becuase of random factors which evolve within the model as it is run (El Nino’s).
261 (beaker): Well, on that point I agree. I just didn’t really grasp what you were getting at.
Beaker: would suggest that there is only one gold standard: observational data. It’s true that there are biases in the data, the instrumentation, the method of collection, and numerous other changes over time. Yet, observational data are the gold standard by which other “assessments” are compared. Without that standard, there is nothing with which to make reasonable comparisons.
The models are meant to attempt to provide some representation of how reality works in a mathematical construct. If the models do provide a reasonable semblance of reality, then the models can be run using different inputs in an attempt to identify the impact of those different inputs (say, increased CO2) on future changes in temperature, sea level, hurricane strenght and frequency, etc.
What the models have demonstrated is that they do not do a good job of representing our gold standard of reality: observational data. If the output from the models is that for a given change in CO2 concentration, it will either get cooler or warmer at a given point in time and a given altitude, then what exactly is the point of the model? What value does one derive from using the model?
Yet, those same models are being “sold” to us as being an accurate representation of reality. The models are being sold to us as having the ability to predict what temperatures and climate will be like in hundreds of years. The level of uncertainty and variability in those models has been downplayed (er, more accurately, not even mentioned in the lay press). The models are being used as the basis for implementing major policy initiatives which would cost trillions of dollars and affect billions of people.
Bruce
Bruce: The observational data may be the best thing we have, but we shouldn’t pretend that it doesn’t have substantial uncertainties in it when trying to infer climate variables (such as trends). Note for a start there are multiple plots in Douglas et al. labelled as observational data. If there were no uncertainty, they would all be the same. I would avoid calling it a “gold standard” as that suggests too much confidence. As a Bayesian, I like uncertainty, it gives me more things to integrate out!
Andrew #255:
That is exactly where my uncertainty as to the current use of flux adjustments comes from, AR4. They certainly don’t deny that the adjustments are still in use, nor do they quantify their use.
I agree with beaker though that screening the model results for those that “seem reasonable” also queers any analysis. It is like if you were throwing dice and got boxcars three times running and took out the throws because they “seemed wrong.” If the dice were loaded, this would be a good way to hide it.
Beaker #137 said:
“Surely the spread in the ensemble reflects the uncertainty in our understanding of the underlying physics (as well as the stochastic nature of the simulations themselves)”
I’m sorry, wishful thinking does not science or statistics make.
Willis Eschenbach says:
Missed this one. Trying to find out if the die is loaded is not analageous to finding out if the models are inconsistent with the data, it is analageous to finding out of the models are biased. That is not the same thing at all. If a model of a die was incapable of predicting a six and you roll a real dice an get a six, that would falsify the model as you would have data that cannot be reconciled with the data. Note if the model of the die couldn’t predict a one either, it might still be unbiased, which demonstrates that the two tests based on the two statistics answer different questions. Douglass et al. use the wrong test for the question they pose.
Willis Eschenbach says:
Missed this one. Trying to find out if the die is loaded is not analageous to finding out if the models are inconsistent with the data, it is analageous to finding out of the models are biased. That is not the same thing at all. If a model of a die was incapable of predicting a six and you roll a real dice an get a six, that would falsify the model as you would have data that cannot be reconciled with the model. Note if the model of the die couldn’t predict a one either, it might still be unbiased, which demonstrates that the two tests based on the two statistics answer different questions. Douglass et al. use the wrong test for the question they pose.
Beaker: not suggesting that there is no uncertainty of the observational data. Am suggesting that without establishing a standard, then testing the models against those standards to assess the validity of the model, then the rest is simply an intellectual exercise. If the range of acceptable output is so large as to be functionally meaningless, then there is no basis for making trillion dollar adjustments an an attempt to change global CO2 concentrations.
Bruce
beaker, I think there is less disagreement on this thread than it appears. If I have it right, you are pointing out, correctly, that in order to do a statistical test you need to ensure that when you compare an observation to a distribution, you have constructed the statistical model so that the process underlying the distribution actually generates observations of the sort you have sampled. Your criticism is that the distribution being used by Douglass et al. does not generate the kinds of observations they had, instead it generates the first moment of the process behind such observations, which biases the test towards rejection.
At this point people get talking past each other. Defenders of the method are overstating the results if they say they totally falsify the models. Likewise it is an overstatement to say that the results don’t at least raise a serious question about whether there’s a warm bias in the models.
Perhaps the test should be done the other way around, by constructing the confidence interval around the observational trend and then computing P-values for the hypothesis that the model generates data governed by the same underlying process. Then each model would have a ranking indicating the amount of support it gets from the data, at which point we could construct probability-weighted averages of model runs.
Ross: sort of, it is basically a matter of the interpretation of the test that is the issue. If Douglass et al had claimed there a was a statistically significant bias in the models with respect to the data, that would have been fine. However, it would also not be anything new. IIRC the Santer paper that they intended to supplant already says as much. The RealClimate article explicitly acknowledges this:
RealClimate said:
It seems to me the modellers were well aware of the bias already.
Beaker #264 says:
“The observational data may be the best thing we have, but we shouldn’t pretend that it doesn’t have substantial uncertainties in it …”
Exactly how can the parameters for a model be worked out if the observational data has “substantial” uncertainties??
I think we all agree that not all forcings are understood even to the sign. Now you are telling us that the models that are supposed to be useful tools were based on data with “SUBSTANTIAL” uncertainties??
Basically you are saying they are wasting their time. THANK YOU.
I want to give what I judge is Beaker’s view of why the proper statistic to use for comparing the 22 model results with a single instrument data set is the standard deviation of the 22 model results and not the standard error of the mean as was used in the paper under discussion. I will do a simple rendition and keep it brief with the idea of showing how a representation of the data could change your statistical measurements.
In the Beaker view, the instrumental data are considered as 1 additional rendering of the 22 model outputs would be. The test he would consider legitimate would then be whether the 1 additional rendering (instrumental result) was part of the population of results by the 22 model results. Obviously in that case one would determine the average and standard deviation of the 22 model results and determine whether the 23rd result (instrumental) was within or without the 0.05 area of the probability distribution of the 22 samples.
On the other hand if I assumed that the instrumental result should be the true “mean” for any number of model results averaged together than one would proceed to look at the model average of 22 samples using the standard error of the mean, i.e. the standard deviation of a point estimator (the true mean) as was done in the paper under discussion.
beaker, I’m not persuaded by your that RC has correctly diagnosed the Douglass et al paper (I’m still reflecting on the Douglass et al paper and by disagreeing with the RC diagnosis doesn’t mean that I’ve come to any conclusion on Douglass et al ). It takes me a while to think about this and it’s not the highest on my priorities.
Let’s define the following sorts of uncertainty building on earlier observations:
1. climate modeling errors; sigma_model
2. stochastic uncertainty in the climate system given actual forcing; sigma_climate
3. modeling errors in splicing different satellites and other errors in the observation model; sigma_splice. Presumably some of the splicing uncertainties will hopefully be contained to the early portion of the record.
4. measurement errors in the satellites sigma_obs
It seems to me that Gavin Schmidt makes an all too characteristic conflation of models with reality when he says:
Thinking out loud, climate models presented to the public are outputs from an industry which arguably has a sort of gestalt. Has it been established that the sigma of the model distributions is an estimate of the stochastic uncertainty? Aren’t they different things?
Elementary statistics for the distribution of ensemble trends can plausibly be calculated as Douglass et al. If dozens of runs from the modeling industry are done, then the ensemble trends will plausibly have a distribution more or less within the Douglass intervals. The variation in the trend of an individual model will have the wider standard deviation argued for by Schmidt.
But what is the stochastic uncertainty of a real world realization? It seems plausible to me that this would be different from either.
Note Gavin’s phraseology “one realisation (the real world)”. If the real world were a realization of a climate model run, then his argument would hold water. But it isn’t. If the uncertainty resulting from erroneous modeling matched the stochastic uncertainty of the climate system, that would be purely fortuitous. Why would this be the case? What is the evidence for this? I didn’t notice any references in Schmidt’s post.
My impression is that the debate is fraught with irony. In effect, Schmidt is arguing for a rather high stochastic uncertainty to save the model gestalt, while the skeptical authors are, in effect, arguing for a rather low stochastic uncertainty in order to reject the model gestalt – if I may express things that way. Both parties seem to conflate matters. Perhaps some of these problems originate in CCSP, on which Douglass et al 2007 appears to be a commentary. My own sense is that it’s a lot more plausible to argue that a number of specific models can be plausibly excluded. Particularly poor performers would appear to be: GISS.er, NCAR-CCSM3, CCCma-CGCM3.1T47, MRI-CGCM2.3.2, PCM, GFDL-2.1, HadGEM1, CSIRO.MK3.0, ISPL.CM4, CCCma-CGCM3.1(T63), MIROC3.2.Hires.
Re: #250
I would add some convenient number to both the denominator and numerator so that the obvious result of both Ts and Tt being zero would give a ratio of 1 and not be indeterminate. The positive adder would need to be sufficiently larger than any negative denominator to avoid division by zero. By the way, as I recall, I have seen the troposphere measured versus modeled handled as a ratio in papers I have read.
#271
I am not a statistician but I can read English and the quote from Real Climate may have said something but it sure didn’t say they “were well aware of the bias already.” What it said to me is that once you recognize that there are a lot of unknowables on each side of the equation then the process becomes truly useful. To do what?
#273
…hits the nail on the head.
Normally a lurker, but having read through this thread, first, I would like to congratulate everyone for remaining (more or less) polite, something which is notably not the case on some other blogs. Firm, yes, contradictory, of course, otherwise why are you posting, but civilised. Next, to attempt a brief summary, it would seem that, while the Douglas paper may have used some statistics and phraseology that do not agree with some writers professional likes or dislikes, it does, by and large demonstrate that the models tested do not agree sufficiently with reality, however error ridden that may be. beaker suggests that the observations are one realisation of a chaotic process, but it’s the only realisation that we have, and if the models don’t come close, then they are of no use for any sort of planning.
As to models, are all of the codes and inputs, parameters, tunings, forcings and whatever else goes into them available for any other scientists to check and try runs with? If not, why are they being given any credence whatsoever? It’s on the lines of “This is how it is, so don’t argue with me!”, which is not how this old engineer sees science done.
Another aspect of models which I have questioned in the past, (and usually got a “That’s not how they are run, so go away.” sort of reply), is very simply, why can’t a model be loaded with as much of the information and weather/climate data from, say 1970, and run? I’d even allow input to include known volcanoes, but if such a run deviates significantly from the measured (I know, inaccurately, perhaps) data, then I would say that such a model needs either work or binning. Until, such a result can be achieved, the models are only interesting, not useful. As I gather , from various posts, some models have been, as it were, run backwards from now to “hindcast” the past, but this doesn’t seem to be as useful as starting from the past and forecasting the present.
Willis, this is OT, but Winston Churchill is also supposed to have made a remark on the lines of, to his nurse, “Have you brought that book that I wanted to be read to out of up?”.
Ross McKitrick, in 270 wrote:
Agreed. But here is what I cannot understand.
The question Douglas et al. is asking is this:
“Are tropical troposphere temperature trends consistent with the warming predicted by AGW theory and by the large majority of the models?”
Given that question, why would models that are not predicting any significant warming have anything to do with answering that question?
If the question was, “Are tropical troposphere temperature trends consistent with ANY of the models?” — then, yes, I can see one must include ALL of them in the evaluation.
But that is not the question we are asking, is it?
262 (Andrew): I think that there is a matter of semantics regarding the definition of “input”. If the models generate their own El Ninos (and other effects), that is a random input from the perspective of numerical systems modeling since the output of a random number generator used. You can then generate multiple runs and perform a statistical analysis over the ensemble of the runs from the same model and use that to test the model. That is the standard approach. And I understand that the physics is different within each model. That is what makes it meaningless to apply a statistical analysis across the different models. The output of the different models will have a different distribution, period. (Even the models with no randomness have a unique distribution…the pdf is simply an impulse function. That doesn’t mean it is meaningful to average them together.)
Reading back, erik in 196 suggested that the IPCC seems to lean toward the assumption that the models are drawn from some distribution around a “true” curve. That is my impression as well. My main question is then still, what possible justification is there for this assumption? If we take a number of models with unknown errors, we can simply assume that reality will fall somewhere between the extremes of those models and that the errors will tend to average out? That would certainly simplify life, but it isn’t scientifically valid. A biased estimate is a useless estimate unless the bias is fully understood. An estimate with an a priori assumption that the bias is zero without robust physical justification is worse than useless. It is dangerous.
If nothing else, I have learned from this discussion not to trust any of the IPCC model-based forecasts. Giant error bars are wrapped around estimates with unknown biases. To 90% confidence!
1,1 Top
The question is, if I have a model that matches, since the actual climate has seemingly random behaviors in various major weather patterns, the sun, volcanoes, etc, can the models ever be made that match up with the seemingly random behaviors that actually happen and not with ones that don’t? Somehow that doesn’t seem possible. Do we have any models that match the past now and the future. Guess we’ll have to wait and see. 🙂
Perhaps the issue is not with Douglas et al but with how the IPCC is assuming things are, and the way things were done based on that, pointing back at them?
I dunno, bunches of points seem valid in some way, and I’m wondering what the hidden actual cause of the discussion might be, if there is one. I’d guess that how people are interpreting the wording in the paper might be it. *shrugs*
What a mess….
One thing for sure, the graph in #144 Willis’ post shows none of the models on their own show what the available observational data shows, so something is wrong. I’d trust the satellites more.
For what its worth, I posted a brief question on RC about whether the response to Douglas et al was adequately dealt with on a blog rather than by peer review. Gavin’s response was that the flaw was so obvious it didn’t need a peer reviewed paper to demonstrate it but “who knows what tomorrow will bring”
I then responded to another comment on the thread that there seemed to be some kind of double standard operating in that , for example, Steve M is regularly criticised on RC etc for blogging rather than writng papers for journals but here was RC doing exactly the same. Needless to say that one didn’t make it through.
Steve Mc, you say:
This is the part of the game that always leaves me speechless. Why on earth do the modelers treat all the models as equals? I’ve never heard of this kind of thing being done in science before, where all theories are given equal weight and then averaged. My only theory is that no modeler wants to call for rigorous testing of the models and exclusion of the ones that don’t make the grade … because, at the end, it might be their model which is excluded.
beaker, I still don’t understand the difference you are driving at. You say it would have been all right if the Douglass paper had said the models were statistically significantly biased with respect to the data, but not to say the data invalidates the models.
As an example, suppose you went to a stock broker. He gave you glowing presentations on his ensemble of 22 financial models. He displayed the model results, which showed how much he would increase your money. You gave him your money to invest, and awaited the results.
When you went to see him again, he said “Ooops … I know I said your money would increase, but actually it decreased. However, my models were not invalidated.” …
“Not invalidated?”, you say, understandably furious. “How can your models be valid when I lost money? You said it would go up, but it actually went down. I should pound your head.”
“Aaaaah”, he says, “but out of the 22 models, one of them went down too. Since one of them predicted the actual outcome, my models are not invalid … they’re just statistically significantly biased, is all.”
“Oh,” you say, “now i see how foolish i was, thank you for clearing away my confusion. I’m sorry I got angry at you for losing my money. I didn’t realize that the models weren’t invalid, they were just biased, I feel much better now. Lucky thing you had that one rogue model in there, though, otherwise they would have been invalid”.
“Yes”, he said, “that’s the secret to successful stock market forecasting. If you don’t test the models, one of them will always be near to the observations. It’s the secret of my success as a broker, by gosh, nobody can say my models are wrong.”
beaker, if 21 out of 22 models incorrectly forecast the sign of some change, I’d say those models are more than just biased. I’d say they are incorrectly modeling the situation, to get not only the size but the sign of the change wrong. This is particularly true in the current case, where it is not only the models but the theory which seems to have gotten the sign wrong.
So is the theory invalidated by the four sets of observational results, or is the theory just “statistically significantly biased”? And at what point does “significant statistical bias” in the theory make the theory invalid?
The question is not “Did any of the models come up with a result which is similar to the observations”. If that were the test, you could just add models until one of them comes close to the observations, then declare that the models are not invalidated, just biased. Since the models give a huge range of answers, this is no problem.
The question is, are the models getting the underlying processes correct? Given the evidence to date, I’d say no. If they were getting the processes correct, they’d get the sign of the change correct. Their failure to do so indicates profound problems with both the models and the theory, not just “statistical bias”.
w.
@283
The error in the Douglass paper isn’t worth the time to publish a criticism of other than as a gotcha, because as Bender said, it’s a pretty blatantly obvious mistake in statistical analysis. Publishing on this isn’t going to advance anything in particular. The conclusions of the paper itself, versus claims made in the numerous press releases by its authors, weren’t particularly revelatory had they not been overwhelmed by this fatal error. This is just another reminder that peer review is a minimum standard and not a guarantee. Although if a stats-minded person was looking to get published I suppose a comment would be worth a shot.
As to criticisms of others publishing or not, most RC contributors are actively publishing. RC is a side project and does not claim to be anything but, AFIAK.
There is a wonderful opportunity here for those interested in advancing the science to become active contributors to the literature. Whether they choose to do so or snipe at sometimes decade-old studies is a choice each will have to make his or herself.
beaker, not Bender- apologies.
Steve-
New articles in Nature this week about computer models.
The first is a “News and Views” about models and decadal variability.
The second/main research article is about hindcasting and agreement with observations, as well as forecasting (both on a decadal scale), which should appeal to a few around here.
Re: #281
Douglas et al. are apparently making the same assumptions as the IPCC, i.e. we have a mean value derived from many climate models and we can compare that to a target/true value which in this case is the instrumental data.
The Beaker/RC approach seems much further removed from reality where the instrumental data is treated as an “equal” with the model outputs. With the Beaker approach, the IPCC should be taking the model outputs and the instrumental data together, averaging them, and calculating a standard error of the means and using that to establish confidence intervals. They might then want to establish what kind of distribution the data forms and determine whether such a distribution has individual results that are out of the established distribution, but I do not believe this is what is done.
I think I’m getting it. If we apply this error distribution to basketball, every time a player drops the ball he scores two points, but my question is, for which team?
That previous post of mine was inadvertantly sexist. Correction “he or she scores two points”.
Jon, in 285 said:
Everyone seems to completely ignore the fact that Douglas used the standard error of the mean because it is the mean that shows good agreement with the surface record and what they wanted to evaluate is whether the predictions of those models in agreement with the surface record are consistent with the observations.
If you want to argue that he should have used the standard deviation instead, at a minimum he should be allowed to exclude models that are not predicting any significant warming. Including those models in calculations using the standard deviation simply makes no sense at all, to me anyway.
Does anyone know what sigma-derived limits look like if calculated solely from models showing significant warming of the tropical troposphere?
— Claudia Tebaldi
Bulletin of the Atomic Scientists
Basically, it is a collective hunch.
erik says:
My understanding is Roy Spenser’s cloud feedback model explains the current observations quite well.
[snip – sorry bout that, Sam, but I view that post as a diversion]
Let’s not discuss alternative theories on this thread. The statistical issues are thorny enough.
#285. I’m trying hard to understand Gavin’s point as he’s a smart person, especially since the point is endorsed by beaker, who also seems smart.
But it seems unmade to me. Perhaps someone to whom Gavin’s point seems obvious can explain to me what I’m missing. According to Gavin, the standard deviation for an individual “realization” of the climate system given the forcings can be estimated by the standard deviation of trends from randomly chosen realization of the models in the CCSP network. From the Douglass et al data compilation (assuming that this has been collated correctly), the mean LT trend from the 22 model sample is 0.2142 deg C/decade and the standard deviation is 0.0978 deg C/decade. (I calculated these using weights provided by John Christy and the data in Table IIa).
Over the 20-year period of the Douglass et al analysis (1979-1999), the range of temperature increases over 2 decades in an individual realization given all the underlying forcings is between a negligible 0.037 deg C and a much more substantial 0.82 deg C. Over the 30 year period which will be available at the end of this year, the range will be between 0.06 deg C and 1.23 deg C, on the basis that the forcings in 1999-2008 are in line with prior forcing trends.
Under Gavin’s premises (all the forcings are known), this range in outcomes – a full degree C in 30 years – is entirely stochastic to the climate system. As I understand it, his main point is that the actual outcome is within this range and thus Douglass et al failed to show an inconsistency between the models and real climate.
Aren’t we then back to square one with the roles reversed? Usually people in Gavin’s camp say that we can’t explain the observed temperature increase without invoking strong GHG forcing. But isn’t the implication of Gavin’s present argument that there is a LOT of natural variability in individual “realizations” which is purely stochastic and requiring no explanation.
I’m not staking my reputation on this exegesis as I’m just trying to follow the arguments here along with everyone else.
Let me see if I have this correct from a layman’s perspective. We have IPCC and cohorts forecasting an increase in temperatures ranging from 2 to 11 degrees by the end of the century.
So if the increase is 3 or 11 degrees they are correct. But if the increase is only one degree they would be out of the uncertainty range. So is Beaker saying that if they had a range of zero to 13 degrees then the forecast would be within the range of uncertainty?
@291
@296
If you drop RC/Gavin from this, the point that my- and not to speak for him but what I think is pretty clear is beaker’s- point is that regardless of the other other criticisms elsewhere of the Douglass et al (and thanks, Steve McI for helping to remind people that it is DouglasS not Douglas, btw) paper, it is fatally flawed by its own framework.
From my perspective, it seems as though there is a lot of fuss over whether or not that means X in reference to Y proposition about climate modeling holds true or not, which is beside the general point that many, many people here seem to ignore and/or not want to address-
The Douglass et al paper is a failure by its own composition. Whatever other ramifications people want to read into it, that is what anyone conversant with the kind of statistical analysis they attempt will say.
I don’t quite understand the position of “besides that fatal flaw, can’t one say X” about that study on a site that spends a great deal of time exposing from my perspective equivalent-or-lesser flaws in other studies. No offense intended, just a little confused.
298 Jon
I guess this is the new mantra from the AGW side of the argument. I believe that “fatally flawed” was also used several times over Craig Loehle’s paper. Did they use it on the Mosberg, Mann, Jones, etc papers — I don’t recall that…….
FYI: April 30 (Bloomberg) Germany’s Institute of Marine Sciences said today that parts of N. America ans Europe may cool naturally over the next decade as shifting ocean currents temporarily blunt GW . Richard Wood, Hadley Center, said “Those natural climate variations could be stronger than the GW trend over the next 10 year period”–but, “if you run the models long enough, eventually global warming will win”. There you have it, run the models long enough, they’ll trump reality.
An easy way to understand the issue is to ask “What random data would Ineed to generate to pass a particular test”.
For the test proposed at RC, I would only need to generate radom data with sufficient variance to encompase the observations, irrespective of the mean.
For the test in Douglass, I would need to generate data where the mean matched the observations. To do this I would need the models to be sufficiently right about physical reality to reproduct the lapse rate change. This matches the intent of the Douglass comparison.
RC slides over the issue that they are not looking at the possible trajectories of temperature over time, but at the atmospheric profile aloft. This is much more constrainted that the time-evolution of the system, and much more theory laden. Thats why it is a test of the theoretical basis of the models (which they fail).
#299 Re:
By dramatizing with alliteration they are just asking to be mocked.
Steve (286)
That’s what I was thinking. Take out the two “outlier” models and you invalidate the model ensemble; leave them in and you invalidate a significant plank of the AGW theory.
These outliers would seem destined to become the bristlecone pines of the climate modeling fraternity (can’t live with them, can’t live without them).
Thanks beaker for outlining the statistical distinctions, it has been very instuctive.
Cheers.
299 (Pat Keating): It’s either that or “discredited” which gets tiresome after a while. I’m sorry but after hearing these epithets tossed around at plenty of perfectly good papers, I’m inclined to disbelieve criticisms like this. I’m resisting that temptation becuase in this case they sound like they know what they are talking about, but I have seen them lie and distort and misrepresent the publication record too many times to just except what I’m told and shut up.
That said, I’d like us to reach a consensus (bleck) in this thread as to what can be said uncontroversially about tropical tropospheric trends versus models. I’m making a presentation and I want to bring up this issue, but not get called on for making unsupportable statements.
I, like Steve Mc, am confused here. It seems to me that, in addition to the important problem of Gavin’s claim of floor-to-ceiling uncertainty posed by Steve, there is also some confusion about what is being measured.
The modelers agree that their models can’t predict an “individual realization” of the climate system. However, they say that they can provide a model of the long term climate trajectory. Here’s a typical statement of the situation, from Professor Alan Thorpe, the head of the National Environment Research Council. Dr. Thorpe is a world renowned expert in computer modeling of climate. He says (emphasis mine):
If individual realizations are not predictable, and “the key is that climate predictions only require the average and statistics of the weather states to be described correctly”, then we must ask whether the increase of temperature trends with altitude (which is both predicted by theory and “confirmed” by models) is an “individual realization”, or whether it is an “average or a statistic of the weather.”
Since we are looking at averages of what has happened over a relatively long period (20 – 30 years), it seems quite clear that it is an “average or a statistic of the weather”. This point of view is strongly supported by the fact that the increase is predicted by theory – in other words, it is not the result of a given “individual realization” of weather. It is something which is determined by the physics of the situation, not just in a general sense, but to the point where we can make theoretical predictions, based on the AGW hypothesis, of both its sign and its value.
Since it is an “average or statistic of the weather”, the standard error of the mean is the appropriate metric to use for comparisons. The idea that one model out of twenty-two getting this critical parameter kinda sorta right somehow vindicates the models is contrary to everything we know about averages. The individual model results are long-term averages of individual runs of each model. The averages of the model results are averages of long-term averages. The averages of the observational data are also averages of long-term averages. None of this is an “individual realization”, they are all “averages and statistics”.
Does anyone have data on any of the individual runs of any of the various models? It would be very interesting to see how much the “tropical amplification” varied between individual runs. My strong suspicion is that it varies very little between runs of an individual model … which in turn would imply that it is not particularly affected by the details of the “individual realizations” of the weather.
But in any case … how can a long term average of years of observations be termed an “individual realization”?
w.
One of the biggest issues which is not a technical/scientific issue but rather a huge political one. You have “climate modelers” doing research in which their piers are also of the same ilk passing more and more forecasts into scientific journals and into the media. None of the models can be validated or falsified:
http://www.telegraph.co.uk/earth/main.jhtml?xml=/earth/2008/04/30/eaclimate130.xml
I can be found on several links stating in my opinion these models are not even worth a bucket of warm spit
304 Andrew
I suggest that the post just before yours by Marine_Shale is a good summary of the situation.
300 Joe S
What he means is “if I can stretch this out long enough, I can be retired before the fit hits the shan.”
Key word “if” they are accurately represented in the model. Few concede that they might not be! But there is one point he misses, also. The overall radiative budget is a powerful qualitative constraint on the climate possibilities, becuase they do not constrain the magnitude of variations so much as their sign and relative amplitude, the former task is done by the climate sensitivity, and this to can easily be misrepresented.
This all started with Ross’s T3 tax. It’s been a fascinating ride.
So Beaker (and Gavin) have posed a problem with Douglass et al that casts a shadow on the findings. A few people have proposed this misses the point of the study. But as compelling as the arguments for why the results are correct “anyway” may be, they ring of Wegman’s response to Mann, “Method Wrong + Answer Correct = Bad Science”.
I am anxious to hear more agreement or dis-agreement with Beaker as most of the comments are not definitive. So did Douglass et al employ an inappropriate statistical method or not? John Christy does not seem one to shy away from an error…if there is one.
@299
I’d rather keep this civil. My choice of language is independent of Lohele’s errors, corrections, or submitted study in the first place. Let’s please stick to the issues at hand.
If you would care to address the statistical failure that I and beaker commented on, please feel free. I’m not quite sure what the obsession with Mann is all about.
Keith, thanks for your comment, in which you say inter alia:
Before we get to the part about “Method Wrong + Answer …”, I seem to have missed the part where someone actually showed that the Douglass method was wrong. Could you point that out?
Once you’ve cited that part, then perchance you could show us where someone said that “the method is wrong but the answer is correct”, or the like. I know it was not me. I have proposed alternate methods, under my perhaps naive theory that you don’t need statistics to tell a frog from a moose. However, I have only done this because some folks out there don’t like the Douglass method, not because I think it is wrong.
Once you have demonstrated both of those, your comment will apply.
Until then, the jury is still out, and your comment is premature.
w.
Jon,
Please comment on Willis’s #305. He seems to be attacking the question directly. I’ve been trying to figure out the lay of the land and frankly, it’s still all mud to me. Admittedly, I haven’t read the Douglass paper yet, but given the nature of the discussion, I’m not at all sure it would help a the present. I need to understand exactly what the debate hinges on and so far Willis’s comment makes the most sense. So I’d like to see what response can be made to it.
Willis–
I suspect the only tweaks the Douglass paper needs is the addition of the standard error for the measured trends at each elevation. This is entirely possible to do. We can do an experiment where we measure 30 guy’s heights. Then, if someone had a model that predicted the heights, we would compare the model prediction to all possible values that conform to reality.
Reality is earth. That’s the climate we want to predict. If we can’t do this with 30 years data, we can’t do it with 100 years data. The only difference between 30 and 100 is the uncertainty intervals associated with any true earth’s climate metric is wider for 30 years than for 100.
The models that fall outside the uncertainty ranges based on the earth’s data are likely wrong.
@312
He does? Please take me step by step how he addresses the Douglass study’s problems. I am having a hard time seeing it.
@lucia
It is a target-rich environment if you are looking to publish a comment; best of luck!
I haven’t read 10% of the comments due to heavy research load – so likely miss many interesting comments. Here is another way to look at Douglass et al. The real world experienced a single tropical surface trend. The trend at 300 hPa from the observations indicates a multiplier factor of about 0.6 to 1.0 of that of the surface. The models show a mean multiplier of 2.01 with a SE of ±0.10. Thus using the ratio test gives the same result that there is very likely a significant difference between models and observations, for whatever reason.
The latest RICH data version of RAOBCORE (this is I believe the 5th version of which I will not point out some shortcomings) comes up with about 1.7 in tropics and 1.0 globally.
I would not be surprised that a factor of about 1.3 could be realistic, but 2 seems much to high.
I probably need to point out for the umpteenth time that our test was a conditional test … If X then Y. The real world experienced one set of tropical surface and upper air trends. Given the observed surface trend, what magnitude of upper-air trends occurred in models? If models were characterized by the same surface trend as that which was observed, their 300 hPa trend should have been around 1.0 that of the surface but was a factor of 2 greater than the surface – a magnitude we don’t see in the observations. I’m repeating myself I see.
There are more ways to study this problem so our experimental design wasn’t the only way by any means, but it was one way, and it was legitimate.
John C.
@ Lucia
http://www.nature.com/nature/journal/v453/n7191/full/453043a.html
Lucia, you may wish to review AR4 projections used in your falsification of IPCC AR4 projections as apparently the data used was misinterpreted, or is this a new and improved IPCC version? 🙂
Let the backpedaling begin.
No. You created your own test. With your own choices. With your own past satellite calls, which I’m guessing not many here remember and/or know what I’m referencing.
You failed your test by your own standards.
How, on a site dedicated to auditing, is this getting a pass?
#235 beaker is [snip]. Almost as much as gavin’s “hey, anything is compatible with my model; I’m irrrrrrrefutable”.
Steve: c’mon bender. More civility to other posters.
There is quite a lot of arguing at cross purposes going on here. beaker and others have pointed out over and over again what they see as a flaw in the Douglass paper. They may be right, but that is not the point, because the data under discussion was not produced by Douglass, but simply used by him. How well do the models match the real world is the central question.
Put the Douglass paper aside and just concentrate on the numbers in Table II.a and the Willis graph at #144. Do the models do a useful job of reproducing the real-world data? Unless there are errors in the Table, then frankly I think the answer is obvious.
@321
It seems as though there are passing few that even ken why the Douglass paper is flawed, and a hole host that want to forget such.
Please, walk me through the Douglass paper and tell me what you think it means.
#322 I don’t quite know how to put it more clearly. Douglass’ method of interpreting the data is peripheral to the main issue, as are the arguments around said interpretation. What matters is the meaning of the data he used.
I have no opinion on the SD vs SE issue, but I can only ask again: from the graph in #144, how can that ensemble of models be regarded as a useful reproduction of real-world tropical tropospheric temperatures?
Good morning all,
J Christy says:
The problem is one of the statistical terminology used in the paper. The test performed demonstrates a statistically significant bias, i.e. the average of the model runs is significantly different from the observed data. However in asking if the models can be reconciled with the data, or if the data are inconsistent with the models, the question becomes “are the data considered plausible by the models?” or in other words “are the models capable to generating the observed data?”. To answer that question, you need to determine whether the data lie within the spread of the models, not that they are close to the mean.
To say that the models are inconsistent with the data (or cannot be reconciled with the data) is a much larger claim than that the models exhibit a significant bias with respect to the observed data, and the test performed only establishes the latter. If you are going to use a statistical test to establish a result, it is vital that you avoid using terms with specific statistical meanings (such as “inconsistent”) if they are meant in a more colloquial sense.
I am not sure what you mean by conditional here, again it is a term with a specific statistical meaning, and I can’t remember seeing any conditional probabilities discussed in the paper.
It was legitimate (ish, for example it would have been better if the uncertainty in the observational data had been included), it just doesn’t support the conclusions drawn in the paper (at least as stated).
I would be happy to discuss this via email if a statisticians viewpoint on this would be any help (I perfectly understand the loading issue!).
jon, someone said:
You replied
No. That’s not how it works. You read what I wrote (in #306 or elsewhere), and you comment on it. If you don’t understand it, ask questions about the part you don’t understand. I went through it several times, from several different points of view. If you have questions, ask them, I’m happy to answer, that’s what we do here is discuss these questions … but I’m not going through it all again just because you aren’t following the story.
For example, you could start by commenting on whether or not you think the averages of the models and data are “averages and statistics”, or whether they are “individual realizations” of the climate.
Or, you could comment on my graph above. See the horizontal blue dotted line that marks the surface trend? What do you notice about the line, the models, and the data?
I have built radiation models myself. They show the same behavior as the GCMs … they show the tropospheric temperature trend rising faster than the surface. Now, I could stand here and argue that by God, my model must be right, the trends have to increase with altitude because my model says so, it’s obvious the observations must be wrong … but given the fact that all observations show the trends decreasing from the surface upwards, and my model (along with most GCMs) shows the trends increasing from the surface upwards, I’d have to say my model doesn’t include some relevant processes.
w.
After reading the Douglass et al paper and the RC response, here are my thoughts:
1. Gavin tries to argue Douglass does not consider El Nino events or volcanic eruptions. Not true. The paper discusses El Nino events and how it is not reasonable to expect models to predict the timing of El Ninos. The paper explains the data covers enough years to minimize differences in timing of these events. The paper does not discuss volcanic eruptions but it seems apparent the same logic would apply, unless the models do not consider volcanic events and would therefore be untrustworthy on that basis alone.
2. Gavin argues that using data from 1979 to present is too short of a time scale. Hogwash. RC is always talking about the warming in “the latter half of the 20th century.” These are the years that warming happened. Temps were going down from 1945 to 1975.
3. Gavin says Douglass et al should have used the updated and “better” RAOBCORE v1.4 version. John Christy in Comment #44 above says they considered this version but that its “unrealistic trend profile” caused them to reject it. They used v1.2 instead. This is the only place I can criticize the Douglass paper. It seems to me if a later version of the data was available they should either have used the later version or explained why they did not. People may think I am picking at nits here but I truly think this is important.
4. Gavin says the most egregious error is the way they calculated model uncertainty. However, Gavin’s comment makes it sound like he did not read the paper. In section 4.2, Douglass et al discuss “Efforts to remove the disparity between observations and models.” They specifically reject the use of “range definition of uncertainty” of model results and explain why. The test Douglass used was more rigorous in that they tested apples to apples, comparing only results where surface temps of models runs approximated observations. This is the same point Christy makes in Comment #317 above. If there was something wrong in this approach, Gavin should have addressed it. Without addressing the issue, Gavin comes off looking uninformed. How can anyone think Gavin scores a point here?
lucia says:
The example of mens heights is a much better one than my dice example. Say we had a model of mens heights that said that mens heights were normally distributed with a mean of 5’10” (70″) tall with a standard deviation of 5″. I could then produce an ensemble of 67 model runs by sampling from this distribution. Indeed I have just done so using MATLAB, and obtained a mean height of 70.41 inches and a standard error of the mean of 0.32 inches. Now I go an measure my own height (as I am the only observable realisation of a man in my office) and find that I am 6’2″ (74″) tall. Now this is way outside the mean plus two standard errors, does that mean that I (the observational data) invalidate the model? No, it just means that the average of the model runs under-predicts my height.
Now try the test again, this time using the standard deviation (2.6 inches) and we find that the mean plus two standard deviations is 75.60 inches, so ay 74 inches I fall well within the error bars, and I am consistent with the model. However, if I was 6’4″ tall, I would fall outside the error bars and I would have invalidated the model (as the model is incapable of generating a member of the ensemble that matched the observation with a reasonable probability).
Does this example demonstrate why the standard deviation should be used rather than the standard error of the mean?
beaker,
I just read your Comment in #324. I see you admit having the same problem as Gavin. You do not understand the study was based on a conditional test.
Here’s the condition:
If the models match the observed warming at the surface in the tropics, do the models match observations at the tropical troposphere?
The answer is no.
beaker, your distinction eludes me: You say:
This seems to be your only objection to the paper. So where is the bright line between “inconsistent with” and “significantly biased”?
It seems to me that you have taken it on yourself to define “significantly biased” as meaning that the observations are more than two standard errors [σ/sqrt(N-1)] away from the mean of the models, and “inconsistent with” as meaning that the observations are more than two standard deviations [σ] from the mean of the model.
Now, while that is certainly one way to define those words, I’ve never seen those definitions myself. Perhaps you (or Jon, or anyone who thinks that you are right) could provide a scientific citation establishing that that those unusual meanings are common scientific usage somewhere.
If you can’t provide such a citation, then you are not arguing statistics, you are arguing semantics — you just don’t like the study using the phrase “inconsistent with” because you’ve made up your own specialized meaning for it which is different from the meaning that Douglass et al. ascribe to it.
Which is your privilege …
… but it’s not science.
w.
Willis #285 The problem is that “invalidates”/”reconciled”/”falsified” etc have more specific meanings than implied by their use in normal speech. All of these terms refer in statistics to whether a model is capable of producing a particular observation, not whether they actually do. However, in a scientific paper, it is vital that technical terms are used accurately, or the results of that paper will be misinterpreted (in this case, grossly overstated). If Douglass et al wanted to point out that there are problems with the models, that is fine, but to claim there is an inconsistency demonstrated by a statistical test is not as the test used is not capable even in principle of demonstrating such an inconsistency (but the standard deviation test can). ~
Willis #329: Actually “bias” is a very common term in statistics, for example
http://en.wikipedia.org/wiki/Bias_of_an_estimator
It is defined as the difference between the expected (mean) value and the true value.
“Inconsistent” has a common statistical meaning that is not relevant on this circumstance, however as we already have a word for bias, the word strongly implies that the data is implausible given the model. I would concede that “inconsistent” may not be defined as having this specific meaning (it would be more natural to state a hypothesis and then say whether it had been rejected), but it would be the obvious meaning to a statistician.
So I suppose you could say it is a one-all score-draw on this issue (being generous to your position).
Now I have given a calm and gentlemanly reply to your rather intemperate and immodest challenge. If you want me to continue discussing this with you then please follow likewise.
I believe the key issue (although there are others) here is whether the record of actual temperature data is indeed a single realization, as beaker asserts, or a collection of realizations distributed according to a common distribution, as Willis argues. In terms of the height example beaker applies in #327, is the entire temperature record a single height, or is each year a single height?
Under the single realization perspective, beaker is right that decades of incorrect altitude/surface ratios could be just an unlucky draw. Under the each-year-is-a-separate-realization approach, it is extremely implausible that an incorrect altitude/surface ratio would keep popping up, year after year. My intuition is that the averages approach is the correct one, because the degree of path dependence in the temperature record cannot be large enough to swamp mean-reverting processes without invalidating the very premise of climatology (“weather isn’t climate”) as expressed by Willis in his #306.
If we can’t treat each year’s data as a separate, independent observation, possibly with some autocorrelation across years, then lots of other statistical tests that seem to be routinely deployed in the climate modeling world would also have to go. We would also have to get rid of the mantra that “one year’s data isn’t meaningful for climate” because the deterministic relationships postulated would imply that we could derive properties of the whole trajectory (though not the precise trajectory) from very small samples if we understood the non-linear dynamics. This just seems very implausible to me, especially given the random forcings (volcanos, etc. ) that hit the system and erase the influence of past values on today’s data.
Ron Cram says:
No, you are missing the point, the standard deviation should be used instead of the standard error of the mean whether or not you add the qualification that the models must match the surface trend. The two issues are entirely different and I have nothing worthwhile to say about the “conditionality” (although I see that point now the way you put it, I had thought it might have meant conditional in the statistical sense, but it doesn’t really it is just a pre-selection of models).
srp #332: the data provide only one estimate for the trend for each altitude, so we have only one realisation of the trend profile for the real world.
beaker, you say:
So you made up your own definition of “inconsistent” as being 2 standard deviations from the mean, and you are upset because Douglass et al. are not using that definition?
Well, that’s OK. Let me give you my definition.
If I promise to make you a lot of money if you invest with me, and I only make you some money, that’s bias.
If I promise to make you a lot of money if you invest with me, and I only make you a few dollars, that’s significant bias.
But if I promise to make you a lot of money and instead you lose a lot of money, that’s inconsistent.
That’s why I would say the models are indeed inconsistent with the data.
Look what we have:
The AGW theory says temperature trends will go up with altitude, because that’s how the physics works, and by gosh, we know the science is settled …
The models all agree with the AGW theory, they all go up except a couple of mutants.
All of the data inconveniently not only goes down, it drops much faster than the models go up.
That’s inconsistent.
Now, back to the math.
w.
Willis #329: Update – here is a reference where the phrase “inconsistent with the data” is used in relation to a statistical test based on the standard deviation:
Reiss et al said:
Reiss et al., “Tests of the Accelerating Universe with Near-Infrared Observations of a High-Redshift Type Ia Supernova”, The Astrophysical Journal, 536:62-67, 2000. DOI: 10.1086/308939.
You can find other examples by using the obvious query in google scholar.
This paper was discussed ages ago. What is this: a student study group?
The title of the post is tropical tropspheric temperatures. The subject is: do the data match the model predictions. The Dougalss et al. paper is one sliver of the whole argument. Trees. Forest.
beaker, you say:
I must be missing something here. Why are there four lines labeled as being observations in their Figure 1?
w.
Willis Eschenbach says:
Sorry, I see the ambiguity, I was referring to one realisation of the actual trend, the lines on the figure are only estimates of this actual trend based on measurements.
In the real world, we ask if the difference makes any difference; if so, then why; and then we ask what we do next if it does.
Willis #335: Your example about making and loosing money is missing an important point. The model ensemble does not give a single point estimate for the trend. They give a distribution of values for the trend that are plausible given the model assumptions. If you only look at the mean (the most likely outcome) you are ignoring much of what the models are telling you.
A more relevant variant on your finance example would be as follows: If I said I expected (another term with a specific statistical meaning) to make X amount of dollars plus or minus Y (representing my 2 standard deviation error bars) and I made less than X – Y, then that would be inconsistent with my prediction. However, if I made X – Y/2, then I would have made less than I expected, but it would still be consistent with my prediction as it is within my stated uncertainty.
The change of sign (profit versus loss) is a red herring as X and Y might be such that zero was within the error bars of my prediction.
Basically there is a difference between a point prediction and a predictive distribution, the ensemble of models provide the latter.
What beaker fails to appreciate is that significance can not be tested when the error structure is unknown.
Error structure in model output is unspecified, and unknown to us.
Error structure in temperature time-series is unknown to anyone.
Therefore there is no basis for comparing the two series.
But we do it anyways – under the ergodicity assumption (srp #322) – that the statistical properties of the time-series averages and the ensemble averges are interchangeable. Is this actually true? I believe it is an open question in climatology.
This is why beaker’s concern about sd vs sem is trivial. Whereas gavin’s remark is central. What are the error structures in the models in the real world? Beats me. Douglass et al. may have made a trivial error, but gavin is making a monstrous error, assuming that this kind of “match” between model and data help to validate the models. That’s not a match, it’s a train wreck.
If the model runs and the observations are different realizations of the same stochastic or chaotic reality, then the standard deviation is clearly the correct statistic, as beaker says.
But runs from different models are realizations of different realities. The differences between the models (as opposed to the runs) are due to errors in representing the same reality. To the extent that these attempts at representing reality are centered on the target, the mean will represent a more accurate measure of the reality, and if the differences between the models are large compared to the stochastic variation, the standard error would be more appropriate than the standard deviation.
But we have a mix of models and runs, so maybe they are both wrong. Also, I don’t think it has been established in this thread that the models runs are realizations of the same reality, as opposed to differences in initial conditions large enough to constitute different realities.
#341
There you have it: Gavin’s fallacy, reprise. Observations are within the range of prediction uncertainty, therefore model is valid. That is NOT how you validate a model. The wider the uncertainty, the higher the probability that the model is deemed valid? What kind of alarmist logic is that?
No. Only if the series are also ergodic.
bender says:
Not correct, if the data fall within the spread of the model outputs they are quite obviously consistent with the model (although that doesn’t establish that the models have useful skills). If you don’t like making distributional assumptions, there is always the field of non-parametric statistics, which is well established and tests hypotheses without making strong distributional assumptions.
#246 Wrong. If you don’t know the error structure you don’t know what the appropriate measure of “spread” is.
#346
You don’t see why your argument is [snip]? Reply to the ergodicity concern. Then you’ll be at the nub of it.
Here are three plots on the side-street matter of tropical LT temperature and SST. They contain no major surprises but are worth a quick glance:
This scatterplot of tropical SST versus LT temperature shows the tight relationship. The loop on the right is the famous 1998 El Nino. (The region covered is 20S-20N and the period is 1979-2008. It uses 5-month smoothed SST and satellite-derived LT data.)
Here is the same plot but with post Jan 1998 points shown in red.
Finally, here is a plot of regional tropical SST and LT temperature. The east/central Pacific swings reflect ENSO. I was a bit surprised at the somewhat correlated behavior of the Atlantic and Indian Oceans, at least that’s the visual impression. The warm and powerful western Pacific is the most muted but probably has more influence on the underlying LT trend than the others.
statstudent #343: The point you make is very interesting, and suggests another way of explaining the difference between inconsistency and usefulness.
Let our null hypothesis be that the physics implemented in the models accurately represents reality (in other words the observed climate and the model runs can be considered stochastic realisations of the same process).
If the model is inconsistent with the data, it means that the null hypothesis is false, so we conduct a test. Following the usual statistical procedure, if the data lie outside 2 standard deviations (assuming normality) the null hypothesis is rejected at the 95% level of confidence and we conclude that the underlying physics of the model is very likely wrong.
However, if the models pass this test the validity of the models is only established in the very weak sense that it is not demonstrably wrong, i.e. that it is plausibly correct, given the uncertainties involved. It doesn’t say that it is a good model.
Douglass et al. may have set out to show that the models are not very good at reproducing this observed trend, but they claim (perhaps unwittingly) to have demonstrated inconsistency, which would be a far more severe indictment of the models.
#349
Sort of what you’d expect if it were the product of a global phenomenon, not a regional one.
This idea that the 1998 ENSO should be excised from any global trend calculation is pernicious. If the major circulatory modes are the pathways through which solar- and GHG-delivered heat flow, I don’t see how anyone can hope to decompose & disentangle the global signal into independent regional and causal fractions. Like em or hate em, GCMs are the only possible approach.
Steve M is correct: temp will rebound after the sharp decline in recent years. Just like it did after ’88-’89.
#350
You are making the ergodicity assumption without stating as much. This is a very dangerous assumption for short-time series sampled from a small poriton of the globe when the correctness of the models is precisely what’s in question.
Prove to me Earth’s climate is ergodic.
Prove to me the GCMs are ergodic.
There is your homework, stats students.
And yet the counter argument by Gavin Schmidt that the ceiling-to-floor uncertainty on the models implies that they are irrefutably correct is equally flawed. Which argument is more flawed? Gavin’s.
Beaker in 327:
It might be a better example, but we still have the same question: are the satellite and balloon measurements of the troposphere analogous to measuring the height of one unit (one man) out of a population of units?
Are the satellite and balloon observations simply one sampling of one place, one altitude and one instant in time — that is, are they a discrete sampling that may be as far from the true mean temperature as the height of a randomly chosen man may be from the population average? OR, are they in fact averages of many such samplings covering a range of places and altitudes and thus represent the true mean temperature?
I think they are the latter, which argues for comparing them to the average of the models.
What do you think, beaker?
Re #37
Another word for “Achilles heel” is uncertainty. So what is the uncertainty on those convective parameters? If no one knows, then no one knows the error structure of the model outputs. snip
The real flaw in the Douglass paper is that the model outputs they are comparing the data to come from broken black boxes. Can anyone blame them for taking them so seriously? They were only following the IPCC party line.
#355 Men’s heights and dice both produce ergodic series. Bad analogues for Earth’s climate?
bender says:
The RC discussion of the Douglass et al paper draws no such conclusion. I posted the last paragraph of it in which he lists several known problems with the models that mean they don’t give a good fit to the tropical trend. That is a long way from “irrefutably correct”! Here is the quote again:
“To be sure, this isn’t a demonstration that the tropical trends in the model simulations or the data are perfectly matched – there remain multiple issues with moist convection parameterisations, the Madden-Julian oscillation, ENSO, the ‘double ITCZ’ problem, biases, drifts etc. Nor does it show that RAOBCORE v1.4 is necessarily better than v1.2. But it is a demonstration that there is no clear model-data discrepancy in tropical tropospheric trends once you take the systematic uncertainties in data and models seriously. Funnily enough, this is exactly the conclusion reached by a much better paper by P. Thorne and colleagues. Douglass et al’s claim to the contrary is simply unsupportable.”
Care for a sample of my own selective quoting?
Re Beaker #327:
Clarification please. I do not understand why you being 6’4″ tall would invalidate the model. All that is happening is that you don’t fall within 2 SD, but you would fall within 3 SD which is still part of the distribution that you are using.
Michael #355: It is my understaning that they compile a single mean temperature time series for the tropics at each altitude and then compute the trend, so it is a single point estimate for each height.
However, the spatial averaging is not the issue. The issue is that had the initial conditions on Earth been slightly different in then the same climate forcings could conceivably have given rise to a range of different observed trends. This means that the real climate on Earth is a random selection of the possible climates that could have occurred given the range of plausible, but unobserved initial conditions. The models, even if the physics was perfect, can only give an indication of the range of plausile trends, they can’t predict the observed one directly as the initial conditions are unknown. This is a pretty subtle point, but it is central.
When IPCC makes a projection, they show the world the ensemble mean from a bunch of models. they do NOT show all individual runs
of the many models. They emphasize the agreement of the models. This agreement is supposed to add support
to the validity of the models. We can thus say that the mean represents the model agreed behavior (best science) and
the confidence intervals on that would be represented in the standard way–2 times se. To compare 2 populations means, you do a 2-sample
t-test. For this you would need info on ensemble mean of observations or test each obs (UAH or whatever)
separately, in which case you need error bars on UAH trend estimates. I believe there is info to test the obs individually, perhaps
mentioned in the paper (don’t have access right now, I’m at a hotel computer in DC). But you do NOT test for a difference
between two population means by comparing the variances.
#358
Translation:
“Our GCMs are embarrassingly crappy, but we can’t admit as much because then the common skeptic will figure out that we don’t know what the AGW fingerprint would look like. And we can’t have that because we have to keep the consensus in order to maintain forward momentum on the agenda. No fingerprint = no ‘smoking gun’.”
See what happens when scientists focus away from facts and uncertainties, in favor of advocacy in pursuit of policy?
trevor says:
An observation outside two standard deviations would be inconsistent at the 95% level of significance, outside three standard deviations would be the 99% level of significance (actually a shade more than that). How many standard deviations you take depends on the confidence you require in the conclusion, but the two and three standard deviations are commonly used as approximately 95% and 99% are convenient figures.
Hope this helps.
Craig #363: True, but you can’t test whether the models are inconsistent with the observed data by testing for a difference in the sample means. That is the test for the presence of a bias.
It would be interestin to see what the actual spread of individual model runs were.
For example, look at willis’ chart and note model 22. that is only 1 run. Look at
the line for model 1, that is the average of 9 different runs. not that it makes a difference to beakers argument, it would just be interesting. One could assume the spread
would go up at the high end.
Beaker says: “Craig #363: True, but you can’t test whether the models are inconsistent with the observed data by testing for a difference in the sample means. That is the test for the presence of a bias.”
So, now I know what he means by “bias”. A test for a difference in means would establish a bias, in a statistical sense. Let’s assume that it would be apples to apples to use the error of estimate of the slopes at each height from the obs data or the se of the 4 obs sets to do a 2 sample test of means. This bias that we establish (the means are not the same) is statistical. What it MEANS is where judgement comes in. If I have large enough populations, a difference in mean height of 1mm between freshmen at 1 school and another would be statistically significant but not meaningful. So if the means from the model ensembles and the means of the obs data were computed properly and a bias found (beaker’s term) or a difference in means found, statistics is finished and human interpretation is needed to say if this difference means something. This is where the fact that the models and theory insist on more warming with altitude and the data show less warming with altitude is a significant theortical (not just statistical) difference, as Willis pointed out. This is not just a statistical question.
Craig #369: The fact that the standard error of the mean goes down as the number of models becomes large shows exactly why the test based on the standard error of the mean does not demonstrate consistency. If we had an infinite number of models the SE would be zero and essentially ALL observed data would be inconsistent with the model, which as you point out is clearly a nonsense. However, the standard deviation on the other hand does not tend to zero as the number of models increases. Instead it tends to a value that provides an indication of the spread of the data.
The standard deviation is a measure of the spread of the data.
The standard error of the mean is a measure of the uncertainty in the sample estimate of the mean. The more data we have the more confidently we can estimate the mean.
Which statistic you chose depends on the hypothesis you want to test. The standard deviation is for consistency, the standard error of the mean is for bias.
Beaker: yes, what hypothesis do we wish to test? The fact that the se goes to 0 with infinite sample size does not make it a bad statistic. What it means is that detecting a difference in means is not scientifically sufficient to establish MEANING in the difference. BUT: you are forgetting statistical power. Any grad student doing experiments needs to prove to their professor that they have a large enough sample size to have sufficient power to detect a treatment difference of a given magnitude (the hypothesis they are trying to test). If they don’thave enough power, they need more samples. We have two treatments here: model and obs. We don’t have a lot of power with only 22 samples in 1 and 4 in the other. So I would prefer a test of 2 means. However, if you insist on testing for outliers, as Gavin also seems to prefer (are the obs outliers beyone 2 sd of the model mean?) then you must test for ALL 4 obs being outliers, which would have a vanishingly small probability.
@363
What does this mean?
In a classical framework, the alpha for the test is chosen in advance. It represents the false rejection probability the researcher is comfortable with so that if the probability of observing a test statistic that is as far or farther away from the value implied by the null hypothesis assuming the null is true (i.e. the p-value) falls below this threshold, the researcher can conclude that the data provide evidence against the null beyond a reasonable doubt. If an alpha of 5% or 1% or 0.1% is appropriate depends on the consequences of an incorrect rejection versus an incorrect failure to reject.
The null for the Douglas et al. paper is that data generated by models matches the systematic portion of the observed data. They then look at how far the results of a sample of series of data lie away from the main characteristics of the real world data assuming that the model generated results form a random sample of all possible results that can be generated by essentially correct models. If the differences between model generated data and observed data are “large enough”, then that constitutes evidence against the null that the models are correct specifications of the underlying physical processes.
Now, if I were checking if the results of a fairly complicated model match observations, I would not have messed with trends by decade etc. There is a another way to check if model results match observations. That is to run a regression:
where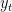 are observed values of the variable of interest and
are observed values of the variable of interest and 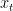 are the values of the variable of interest generated by a model. If the model accounts for all systematic variation in
are the values of the variable of interest generated by a model. If the model accounts for all systematic variation in 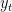 , then the joint restriction
, then the joint restriction
must hold.
If the model generates series for many variables of interest (as GCMs do) then a SURE model sounds to me like an appropriate way of testing jointly that all intercepts are zero and all slopes are one. Failure to reject that would mean confidence that model predicted values for key variables do not deviate systematically from observed values.
I would do this test for each model separately by conducting multiple runs of each model and averaging the results for each variable within model.
Now, if I could only figure out how to run these models. 🙂
— Sinan
Ray Pierre has this comment on Revkin: http://dotearth.blogs.nytimes.com/2008/04/30/climate-science-moving-from-projections-to-predictions/#comment-31324
His comment might make sense if the models had demonstrated that they can provide useful predictions. However, this about face on the PDO more or less proves that the models are useless at doing anything other than extrapolating a linear trend based on past data. (If someone disagrees please provide a reference to a model that predicted the PDO phase change *before* it was too obvious to deny.
Craig #369: The point I have been trying to make is that Douglass et al. perform one test, but then draw the conclusion that would be appropriate had they used
the other test. The conclusion they draw (inconsistency) is a more severe indictment of GCMs than is supportable with the test that they actually performed, which can only detect bias. As a result, the significance of the Douglass et al. study is being vastly overstated, especially in the media.
You mention testing for outliers, that is an excellent way of putting it. Saying that there is an inconsistency between models and data is exactly the same as
saying the observed data are an outlier according to the model (i.e. an observation that the models consider to be so rare as to be implausible). If Douglass et al. were not claiming inconsistency, but that the models provide a poor fit to this trend there would be little controversy, for a start there are already papers that already make that conclusion, as noted in the RC blog.
Did you see, R, how Andy talked up the new usefulness of models? How they are now being tweaked with real data, like ocean temperatures, in order to improve their predictions?
=============================
Re #367
This isn’t beaker’s term it’s a standard term in statistics, check out ‘bias/variance’ decomposition.
Sort of like how confidence in the models is vastly overstated?
Goose, gander.
At the risk of being an annoying newbie who came out of nowhere to sound of like a broken record, I am going to say once again that the error bars added on by RC are meaningless. As an analogy, lets try to model humans by taking a few gorillas, chimpanzees, bonobos, orangutans, and one gibbon, while acknowledging that the systematic error in the DNA sequence of each model ranges from approximately 1 to 5 %. However, if we find the average of the individual ape species weights to give five different numbers, and then average those five different numbers with equal weighing to get a “model average”, it comes out pretty close to the weight of our human sample, Joe. Therefore, we conclude that the systematic errors average out, and we can trust the models for all human parameters. But then along comes someone who follows the same procedure to estimate height, and finds that the model average is very different from Joe’s height. But not to worry. Since we included the gibbon in the model set the error bars around the model average are so large that Joe’s height falls within them, so we conclude that the models may still be used to predict any human characteristic.
Replace the non-human apes with climate models, DNA sequences with physical
processes, Joe with the Earth, weight with surface temperatures, and height
with tropospheric temperatures, and you can see what a statistical mess this is.
If GCM time-series are non-ergodic then Gavin’s statistics are crap.
If Earth climate itself is non-ergodic then everyone’s climate statistics are crap.
Prove to me these things are ergodic. I am willing to be convinced by data.
Chirping on about which statistic best measures spread is pointless unless your time-series and ensemble statistics are interchangeable. Ergodicity is the elephant in the climatologist’s room. No ergodicity, no trend statistics. Robock rules. Cohn & Lins & Koutsiyannis correct. Pierrehumbert humbled.
Re: beaker @350:
“Let our null hypothesis be that the physics implemented in the models accurately represents reality (in other words the observed climate and the model runs can be considered stochastic realisations of the same process).”
Should not the null hypothesis be the reverse? IMHO the burden of proof should be on the modeller, just like in clinical trials of new drugs the null hypothesis is “no effect”, and that is the hypothesis that pharmaceutical companies have to reject. I do not think it is statistically correct to claim that “a model works unless it can be rejected at the 95% level”. Hypothesis testing is always done the other way around.
I am not taking any position on sd vs. sem…
Just my 2 cents…
Exactly. Averaging across models makes no sense.
bender #320 says:
[snip – I’ve snipped the original comment due to the tone and thus the response]
You understand models?
Is this the bender who accused climate scientists of scissoring zonal average model output south of 70S between 1000 mb and 700 mb to hide an alleged model-observational data discrepancy, without first checking observational data (Fleming et al. 1990, Adv. Space Res.) to see if such an area exists in the real world? Hey bender, what’s the atmospheric pressure at the south pole?
Oh yeah, beaker is right.
Douglass et. al test whether an instrumental value is within a certain range from the true mean of model output.
The ‘true’ mean is an exact value.
The range is arbitrary.
No one (sane) expects observational data to match an exact model mean.
Keep going beaker.
bender #354 says:
He never said that.
Translation: Nothing to see here. “Our” guys messed up, no need for an audit. Quick, sneer at Gavin!
bender #356 says:
… so the flaw pointed out by beaker is not real?
Then improve on them. Or sneer at the troops in the field, who have greater knowledge and ability.
Back to the point of this thread.
Ross McKitrick has proposed that the carbon punishment be scaled to suit the magnitude of the carbon crime. Brilliant. Crime & punishment. Equality of justice and a clear deterrent effect. Brilliant.
The question, beaker et al, is: how do you estimate the magnitude of the carbon crime, given that gavin schmidt, judith curry et al. admit it is not possible using current GCMs to identify the characteristic fingerprint of AGW?
Pierrehumbert assures us that the GMT trend will revert back to a rising phase. “I believe, I believe!” But at what rate, sir? And can you give me error bars with that?
Re: 379
Nope. Models can be wrong in infinitely many ways but correct in only one way. That is, under the null, we can calculate the conditional probability of models generating something that is as far away from the observed that as we see the models generate. Then, if that probability is small enough, we say that there is evidence against the null that models are correct.
Hypothesis testing is always done this way, contrary to whatever you might think.
For example, in testing whether a drug is effective, the null hypothesis is that there is no difference in patient outcomes between the drug and placebo.
In testing whether the drug is safe, the null is that there is no difference in side effects between the drug and placebo.
You can conclude that a drug is both safe and effective, if the former is rejected and the latter is not.
But you do not start from the hypothesis that the drug is not safe.
Sinan
Pedro S #379 : That is a bit of a philosophy of science issue, according to Popper, theories (or by extension models) can’t be proved by observation, only falsified. Statistical tests almost invariably end up rejecting a hypothesis by showing that it has consequences that are inconsistent with the observed data.
Statistics provides a mechanism to determine whether one hypothesis is better supported by the data than another (Bayes factors), but it is not generally possible to demonstrate that any model is unequivocally valid.
#381
Whether beaker is right or not is immaterial. The issue is: “what is the AGW fingerprint”.
How much more improvement will it take (in man-years and millions of $$$) to get a well-resolved impression of that fingerprint?
You are trying to make my skill and ability the issue (ad hom) when the substantive issue is model fit to data. I will concede that I am not immune to error if you will concede that we do not know what the AGW fingerprint will look like.
Beaker: further on test for outliers. We have a mean and variance for heights of a population A and a sample of 4 professional basketball players. The test for outliers would consider that the 4 sampled heights could be above and below the mean with equal probability. If the 4 players are let’s say at the .2 level of the population variance, the probability that all 4 are that far from the mean is .0016 (without correction for all 4 being on 1 side of the mean). So we would reject the sample of 4 players as being “random samples from the population”. The same test for the Douglass paper would also reject the 4 observed trends as being random samples from the distribution of model results. If someone can compute that please do, I have no access to computing at the moment. So if you prefer to look at it as outliers from a distribution, you still reject the ability of the models to produce the observed trends as outputs. Just plotting the 2 sd curves and showing they get close to the data is not proper statistics. I do not agree that Douglass et al did it wrong, but if you look at it as Beaker prefers you get the same answer.
Surely everyone cane agree on one thing. Isn’t it bizarre that an elementary statistical concept like standard deviation is a matter of debate in climate science. Regardless of whether the peer-reviewed article Douglass et al is right or Schmidt’s post at realclimate is right, this is something that should not be at issue among professional scientists.
Having said that, I am completely unconvinced by beaker’s reasoning, less and less so and for two quite different reasons. There are some issues related to the concept of an ensemble, which I’m not going to discuss here. For now let’s work through the example of Beaker’s height, one that he provided. I submit that there is an important and relevant difference between the uncertainty that one would expect from estimates made of his height, depending on whether you viewed Beaker as “one realization” or as the real Beaker. This seems like the sort of thing where people should be able to define things sufficiently so that everyone can agree on all the steps as all the issues are very elementary, and the problems arise mostly in language.
So let me try a couple of examples and see what can be agreed on in these examples, building on the height estimation example. Let’s suppose that Beaker’s height were a matter of international import and that 22
agencies were funded to investigate the vexing question of Beaker’s height.
Case 1
Let’s suppose that we knew nothing more about Beaker than that he was an adult man between the ages of 40 and 50 living in (say) Australia – which he isn’t, by the way. Let’s also say that the true height is 70 inches with a standard deviation of 2.6 inches. Let’s also say that the agencies are not permitted to measure heights in Australia, but are permitted to guess a person’s height and, based on experience in other jurisdictions, can make an unbiased guess as to a person’s height with a standard deviation of 2.2 inches – a value intentionally different than the population sigma.
Let’s say that the agencies attempting to estimate Beaker’s height are penalized heavily for being substantially wrong (rather than richly rewarded for making a lucky guess which would lead to a different strategy.)
A plausible strategy for the agencies would be to make a random sample of Australian men in the appropriate category, have their experts guess the heights of each man in the sample and then take an average – which would be submitted as their official estimate of Beaker’s height.
Under such circumstances, the guesses are going to be heavily concentrated around 70 inches and the standard deviation of the estimates is likely to be rather small, probably much less than half an inch.
Beaker is then revealed and his height taken (74 inches), well outside the standard deviation of the estimates, but well within two population sigmas of the population mean.
In this example, it is very clear that the variance of the distribution of the estimates cannot be used to estimate the population variance.
Case 2
Let’s suppose that making a height estimate is very complicated and takes two years to do, so that the agencies can’t do a lot of sampling. Suppose that each agency then picks one Australian man at random and spends two years estimating his height. Then the mean of the estimates would once again be 70 inches, but the standard deviation would be more or less the standard deviation of the population (2.6 inches) with a 2-sigma range from 65 inches to 75 inches.
Case 3
Let’s say that the real Beaker is made known to the 22 agencies. Or that enough information is provided to the agencies that, with a little detective work, they can identify Beaker. Once again, the experts guess as to his height but this time after seeing the real Beaker, rather than a random selection of Australian men. Once again, let’s say that their guesses are unbiased with the same standard error as before – 2.2 inches.
Under these circumstances, the average of all the (unbiased) guesses would be Beaker’s actual height, 74 inches and the standard deviation of the average of all the guesses from all 22 participants would be the standard error of each individual guess (2.2 inches) divided by the square root of 22 ( i.e. 0.47 inches).
Example
Now let’s suppose that we have a “real-world” set of estimates and we wish to evaluate whether the agencies did a good job or a bad job. Let’s suppose that the real Beaker is identified to the agencies or enough information to identify the real Beaker, but the agencies still come back with a set of estimates with a mean of 70.2 inches and a sigma of 2.4 inches, differing little from a random sample of the original population as in Case 2.
It seems to me that the confidence intervals of Case 3 are the relevant ones if the real Beaker is known (corresponding more or less to the assumptions of Douglass et al). In the example, one can conclude that the agencies have either failed to study the actual Beaker or that their methods are wrong or both.
If someone (e.g. Gavin Schmidt speaking in this case on behalf of the popular Australian blog, real height) argued that Beaker was only “one realization (i.e. the real world) drawn from the distribution defined by the models”, people in this case would easily say: so what? He’s the “realization” in question. The obligation of the modelers was to deal with the real Beaker, not a distribution of potential Beakers. In this particular case, if I’ve got the Bayesian terminology right, we had prior information as to who Beaker was and the agencies need to use it. In the climate case, it’s the same. One of the relevant priors is that we’re studying Earth between 1979 and 1999 – we’re not studying distributions of models.
Again it’s baffling that such elementary points should be a matter of debate. Most of the problem is that everything is couched in debating terms. It should be possible to specify a list of cases that people can agree on and let’s try to deal in specifics and avoid generalities.
Craig: RC already did this, they showed that there are trends from observational data that lie within the 2 sd error bars when computed correctly, which shows there is no clear inconsistency (as it depends on arguments about which observations should be used). This is without even considering the error bars on the (estimates of the) observed trends. So the models do not consider the observed trends as outliers (at the 95% level), showing that there is no inconsistency.
As I said, this doesn’t show that the models are valid or even useful, just consistent in this narrow statistical sense.
Lazar, your translator isn’t working. Let me try:
All audit is good; let it be open and transparent from all sides. Audit is most valuable when it is focused on issues that matter. Admitting errors, estimating uncertainties is a part of doing good science. Wish that model uncertainties were handled more expertly by the skilled and able keepers of the consensus. It’s such a critical part of evaluating the strength of AGW response.
Hmm, mine works.
#387
To continue your example. Beaker’s one current height is NOT the issue. It’s beaker’s future height. This is all about trends into the past and future. Therefore it is the class of all possible heights that beaker could have had right now that matters. Why?? Because this bears on what his future height is likely to be.
This why ergodicity matters. You are trying to make inferences about the future based on the past. You need proof that the past trend is not spurious to credibly predict it will continue into the future. That depends not on the current climatic state & trajectory (the single realization), but the functioning of the climate system, as represented by all possible realizations (i.e. the ensemble). In the observational world you can not know this ensemble. In the model world you can. But whether the model world’s knowable ensembles are relevant is precisely the question to be asked.
But you are right: It is absurd that climate science can not get its statistics straight. That is why Wegman is so relevant.
Steve: bender, doubtless a relevant issue at some point, but let’s try to at least establish a few building blocks first. It’s hard for me to believe that people can’t agree on practical cases. So let’s start there.
Beaker: I don’t think you read my post. The proper test is not if SOME obs data fall within the 2 sd of the models, but that all 4 of the obs fall on the same (low) side of the mean of the models at a similar distance from the mean. You need to multiply the probabilities. We have 4 independent estimates, not 1.
I think the arguments are over for me — as I will summarize. The model outputs cannot be considered at the same level of reality as the instrumental measurements. While there are some uncertainties in the instrumental data one can assume it can be considered a proxy for the true mean and that the many models renditions should have an average within the statistical limits of this “true” value. If the instrumental value were considered at the same level of just another model output than one would use the standard deviation in this comparison. If the instrumental data is assumed to represent the “true” value, i.e. the mean that the models are attempting to emulate than I would compare the averages of the models using the standard error of the mean as was the case in the Douglas paper.
I find the latter approximation of the real world (using the standard error of the mean) much more helpful than considering the instrumental data on the same level as the model output. One makes assumptions in either of these cases to make the statistical tests, but as long as one realizes what these assumptions are I think one can obtain some real insights into the differences in the ratios of tropospheric to surface temperature trends between the climate models and the instrumental data. To look at the analyses in the Douglas paper with what I consider an unrealistic view and claim over and over again that a fatal error in statistical analysis has occurred would appear to me to be an attempt to avoid discussing the major point of the paper.
By the way the men’s height analogy should be comparing a sample of men’s heights with a known true average of men’s heights and attempting to determine whether the average of the sample is statistically the same as the true average – using the standard error of the mean of the sample.
#390
Agreed: practical cases are a good starting point. But as I said before, adult heights and dice are really bad examples because (a) they produce ergodic outputs, (b) we know a priori they don’t exhibit trends. Where trend forecasting is dicey is when the internal noise structure is time-dependent (and space-dependent) and therefore non-ergodic. This is certainly the case for any GCM. Your examples need to embrace that kind of error structure. That is what LTP is all about. Dice and heights aren’t going to get you there.
381 (Lazar): You seem to be confused about which “team” bender is playing for. I see him has more of a cynic than a skeptic. He has had a few choice words for us, to.
Hm, interesting the types that come out of the woodwork when the Douglass paper is mentioned…I’m not conspiracising (is that the right word?), just find it odd.
BTW the paper has recieved scarcely any media coverage at all, so I don’t know what beaker is going on about it being overblown by the media. There was one sloppily written and confused story on it on the Fox News website, a press release from UAH, and that was about it (apart from blogs). Not saying that it should have gotten more or less, just that I don’t consider that a whole lot of coverage (none period in the MSM).
#394
bender is a POV. A POV that scans for denial propped up by bad logic and bad statistics on both sides of the fence.
Steve: Firstly, it may be bizarre that we are discussing standard deviations here, but at least now I have an understanding of why this particular error didn’t get picked up in peer review as I have a better idea of how a climatologist would view the paper.
I don’t think any of those cases are quite right. So I’ll have a go at one of my own.
Case #4
There is a single realisation of beaker (forgetting for the moment the impostor that used to appear on the Muppett show every now and again). The task for the
22 agencies is to estimate beakers true height given some uncertain information about his component parts, for example femur length, for the sake of the argument, the agencies are told that his femur is 18″ long with a standard deviation of 1″. The agencies each then perform a study of human males to try and infer a rule that gives height as a function of femur length, however the rule will be uncertain as it is based on a finite sample of data. As each agency used different data and possible different assumptions, each agency will come up with a different model, resulting in stochastic and systematic uncertainties respectively.
Each agency then makes a prediction of beakers height and stores it in a global database of such predictions. The clever agencies submit more that one prediction (forming an ensemble) that represents a sample from the distribution representing the stochastic uncertainties. The database then contains an ensemble of predictions that represent the stochastic and systematic uncertainties in the models used by the 22 agencies.
If beakers true height is more than 2 sd from the mean of the ensemble, it means that the 22 agencies between them can’t reasonably explain how someone with a femur length of 18″ can be 6’2″ tall, and the data is said to be inconsistent with the models. That is what is implied by inconsistency in a statistical sense.
Now there is an additional problem, which is that we can’t directly measure beakers height, so there is uncertainty in the data as well (pehaps we only know how tall beaker is by asking Dr Bunsen Honeydew). This complicates matters, but if the data are within 2sd without considering this form of uncertainty, they will still be inside 2 sd if we do, so we can ignore it for the moment.
Now, how should the agencies use the models. Well, one thing they shouldn’t do is use the ensemble mean as a confident prediction of the future climate. At the very least they should quote error bars. If they want to predict say loss of polar ice, they should run the predictions from each member of the ensemble separately through their model that works out polar ice loss from temperature. They would then have an ensemble of predictions of ice loss, which would give a proper indication of the uncertainty in the ice loss, which they could show using e.g. a box plot.
Does that explain my viewpoint any better?
#392 KF
If the argument is over for you, that would be a shame. Andrew’s treasured “internal climate variability” is what is so damning to the idea that any one realized observation is (1) indicative of the “true” (i.e. ensemble) mean of a process, (2) directly comparable to a computer-generated ensemble expectation.
Also, comparing means within years is one thing. Comparing trends across years, quite another. People are talking about the former. It’s the latter that is the real issue. GCMs produce ceiling-to-floor uncertainty on trend statistics just as sure as they produce ceiling-to-floor uncertainty on means. The fingerprint is not known. Contrary to what the consensus keepers preach.
Now the argument is over.
Very interesting back and forth but I can’t help see the debate I witnessed in a gradate seminar of theoretical statistics many years ago. The discussion was frequentist versus Bayesian views of reality. Isn’t that one of the subplots (if not the most important one) being discussed here?
Re: SD vs SE
Is this not the same question that comes up in basic regression? Are you predicting the conditional mean of Y given some value of X versus predicting a single value of Y given some value of X? This gets back to CIs around the regression line –the former are tighter than the latter.
I am a long-time lurker that doesn’t have the statistical background, so I am just trying to understand. Using the height analogy, doesn’t the graph show that the average adult is around 5′ 2″ based on the actual measurements but the model shows the heights clustered around 5′ 11″? It would seem that, yes, it is conceivable that the model could include the 5′ 2″ people but that it is generally way off the mark and needs to be reviewed. That would especially seem to be the case if the models have some core assumption that people are thought to grow to at least 5′ 6″.
The issue of whether SD vs SEM is the right measurment / validation tool is way outside of my experience to comment on, but it seems that we can say that the models have a higher level of error than I thought they did based on how the whole AGW argument is presented in the popular press.
Here’s a good one. See the chart on observatons versus the model.
http://news.bbc.co.uk/2/hi/science/nature/7376301.stm
One model with the oceans, the other model without. Observations fall in between
Conclusion?
As Eggplant fan said, a statistical mess. 🙂 srp’s right, weather’s not climate. Climate is average weather. So what’s the difference? Climate models are based on weather patterns. Over time. And over space. Or as Thorpe said (in Willis’ quote):
That sounds like a reason to compare means.
The height analogy doesn’t work. What if I sample a school and miss all the basketball players? How about only the 6th graders are there that day at a K-6 and I miss all the shorter children?
The issue here is that much like Steve said; can we compare average heights from an ensamble of various schools where (unknown to us) 5 K-6 schools 10 junior high and 7 senior high (some from samples of students, others from student records, in some unknown mix) to 1 college’s doctorate program based upon who’s showed up that day?
It’s like the anomaly. Consider 1 site. Over the month we sample the air at that place and time 5 feet up, get the high and low measured, get a mean. Then we combine the means of the 28 29 30 or 31 days. Then get an anomaly. Then we combine 12 months. What are we getting? What was going on 20 feet up 500 feet away?
I agree with bender. We don’t know the error structures, we don’t know what the spread it, things aren’t ergodic. We end up with things we can’t really compare. We get some ranges with error bars big enough to fit an elephant. I think the thing here is the question; are the mean of the models inconsistent with the measured satellite records, at all altitudes separately? Oh, problem. The real world doesn’t have distinct separate altitudes, it has a mix.
Michael Smith:
Re: Steve
Each agency’s guess is a random variable. If the Central Limit Theorem is applicable, the averages of guesses will be distributed normally around the true mean guess. It is then a legitimate question to ask if the true mean guess is close enough to observed datum. Which means, standard error of the mean guess is the appropriate denominator to use in the test of difference between the true mean guess and observed value. (Standard error of the average guess is nothing other than the an estimate of the standard deviation of average guesses).
— Sinan
Steve-
Pretty funny how people just want to argue here. I’ll try again to add something objectively that was missed earlier.
Here is a letter in Nature this week that uses the ECHAM5 (one of the European GCMs) to hindcast SSTs (including the tropics) from the 1960’s to present and compares the ensemble mean with observations – which is what people have been asking for. They then show a short 15 year forecast. Instead of reporting yearly results, they are using decadal averages. This isn’t my area, but it may give people here something else to talk about…
Think about this. The Figure in #85 implies that a realized cooling trend of -0.18C/decade at pressure level = 100 could be consistent with AGW hypothesis as represented in the GCMs. That’s quite some hypothesis test, isn’t it? Cooling “is consistent” with warming.
I confidently predict that one team from North America will win the Stanley Cup this year. And when I’m proven right, I’m sure beaker and Jon and Lazar will worship my foreacasting skill. I will have some stock to sell them.
Leave the dice and demographics alone. Think stock markets or professional sports. Will the bear market continue? Will the Flyers/Penguins/Red Wings sustain their momentum? Or will they tank? Now you’re on fertile ground. These are multi-causal dynamic non-ergodic process. What causes a team to streak or skid? CO2? (Sport is fundamentally a respiratory process!)
Beaker: As i walk down the hall, 4 doors open and all 4 men that come out are over 6 ft 6 in. Would you test for outliers by saying that the distribution for men’s heights includes that height (nothing to see here, move along) or: looks like a basketball team! Maybe I can get an autograph!
Re: #404
And the better analogy to use for the Douglas et al. analysis. It appears to me that Beaker is not addressing this view.
405 Jud Partin
I wouldn’t call it arguing, moreso trying to come to an understanding on what is being discussed exactly. In this case, it appears mostly trying to define what “inconsistent” means versus what “bias” means, and how much statistics applies, and what to do statistically to test the hypothesis under question; do the models as an average reflect, within some constrained range that’s realistic, what’s going on at an area of the tropical troposphere.
Or in other words (lol) if this is a statistics question, we should use those terms. If it’s not a statistics question, we should use English instead. 🙂
RE 411. You missed the joke
Kenneth Fritsch says:
The point is that you can’t test for inconsistency by comparing means to see if there is a statistically significant difference, however it is the right thing to do if you want to test for bias. Now whether bias or inconsistency is the issue of real interest a debatable point, however Douglass et al claim inconsistency, so they used the wrong test for what they claim.
The problem as I see it in this discussion is that there is a difficulty in separating what Douglass et al. actually did and actually claimed (which was the point I raised) from what question Douglass et al. meant to address or should have addressed.
I am not saying that the models should be tested for consistency, just that if you want to claim inconsistency then you actually have to test for it.
Willis…from a comment way up there
I’m sorry if you were offended by my comment. I appreciate your comments and graphics. I also understand there are multiple topics occuring within this thread. I am not looking to point fingers, and I did not name anyone. I have not accused you or Douglass et al of “bad science”. I am suggesting that to discount the criticism as unimportant because the result is correct for some other reason is what Wegman warned against. It does not suggest the issue may not be viewed or explained differently. It only pertains to responses to the criticism of the Douglass paper.
When Craig Loehle published his paper, there was specific criticism. The statistical group seemed to agree. Craig revised his work. Perfect.
In this case the criticism does not seem to meet much agreement. If staticticians don’t agree on a statistical method to use, I would hardly expect climate scientists to be certain of the statistical approach to use. So you may be right that my comment was premature, but I am still looking for a more definitive direction.
Beaker asserts it is wrong as does Gavin. Do I know the correct answer? absolutely not.
#398 beaker:
Let’s take your version and run with it. You say, “As each agency used different data and possible different assumptions, each agency will come up with a different model, resulting in stochastic and systematic uncertainties respectively.” That means that the estimates of the model can differ from the actual height for either of two reasons: Systematic uncertainties (read “statistical bias”) or stochastic uncertainties (read high variability in the estimation process). It appears to me that the former reason is the more important one for modellers because high variability can be overcome by increasing the information with repeated runs, but the systematic bias will remain.
What are we testing here? Put it into hypotheses: H0: There is no systematic bias in any of the model results. HA: One or more of the models is biased. OK, how would you test this simply? I would test whether the mean of the “population” of model “observations” differed from the value(s) they purport to estimate. One way, is to form a confidence interval around the mean of the model runs (using the standard deviation of the mean and NOT, as you propose, the sd of the data. By this criterion, we would reject the null hypothesis and conclude that the set of models contains one or more with systematic bias. I would not object to a statement that the models, as a group, were not consistent with the observed data. By the way, the definition of “consistent” that I know and love in statistics is an adjective applied to an estimator indicating that the estimator converges in probability to the parameter being estimated as the sample size gets large.
What appears to me to have become a point of confusion is that to show that a particular model or models were “inconsistent” with the data, you would need to get a handle on the non-systematic variability for each model – what ostensibly you are proposing with your 2 sd error bars. Because of the unknown biases in the models, this cannot be estimated from the model results as shown and would require multiple runs with each of the models to extract that information in a useable form. To imply that somehow a single observation from a model gives evidence of “consistency” for that model is one of the (I blelieve valid) objections being raised in some of the responses. Of course, there is still the obvious question that given a lack of systematic bias, if the models differ by such wide margins, what is the value of results based on so few runs?
Beaker, may I offer a refinement to the “case” you outlined in 398?
First, we are really asking the 22 agencies to predict TWO separate heights: we’ll call one the “total height” and the other the “foot-to-waist height”.
Now suppose that 20 of your agencies developed a ratio of height to femur length such that they predict a “total height” of 70” and a “foot-to-waist height” of 35”.
The other two agencies develop a different femur to length ratio such that they predict a “total height” of 60” and a “foot-to-waist height” of only 25”.
When we measure you, we find an actual “total height” of 60” and a “foot-to-waist height” of 35”.
Assume a standard deviation of 2” on all estimates.
Obviously, the group of 20 modelers has got the “foot-to-waist height” nailed but are way off on the “total height” — while the other 2 modelers have mailed the “total height” but are way off on the “foot-to-waist height” .
If these two groups of models were evaluated separately, both groups would be rejected. But if we combine them, then there is sufficient variation that the two sigma limits encompass both heights and we declare that the models and the observed heights are not inconsistent.
Would that procedure be logical?
Just a few quick points before I go home.
Keith #413 : I am certainly not asserting that Douglass et al is bad science, just that their interpretation of their test is a non-sequitur, judging from the discussion here probably an unintentional one through not appreciating what is meant by “inconsistency” in a statistical sense. The paper would tell a useful story if revised slightly to claim significant bias instead (and maybe add a few caveats about uncertainties that had been neglected).
Roman #414 : The hypothesis is determined by the claim of inconsistency in Douglass et al. Consistency requires that the observed data are in principal reproducable by the models, if even one model run replicates the data reasonably closely then the models have demonstrated their consistency. The fact that consistency is such a low hurdle is exactly why inconsistency is such a big claim.
As I said consistency doesn’t imply useful skill, it just means not demonstrably wrong (in probability).
Beaker says: “if even one model run replicates the data reasonably closely then the models have demonstrated their consistency.” Let’s follow that thought, which reflects also Gavin’s point. What the IPCC presents is an ensemble mean and theory that both say the mid-troposphere should warm more than the surface. Nowhere do they say that the theory includes cooling as an option, and it was noted by someone that Greenhouse theory REQUIRES warming of the mid-trop to get a greenhouse effect. To claim that because some model gives a cooling response there is consistency is to ignore that it is the aggregate model response that is supposed to be robust, not all possible models. Furthermore, the particular models that show tropo cooling also do not give much warming at the surface over the next 100 yrs (I believe that is in the Douglass paper, correct me if wrong here).
Craig wrote in 417
Yes, that is noted in the paper. Essentially what is happening is that models that are wrong about the surface trend but correct about the troposphere trend are being averaged in with models that are right about the surface trend but wrong about the troposphere — with the resulting variation created by those differences giving rise to a large enough standard deviation that one can claim that the models are not inconsistent with the observations.
That’s what I was trying to show in comment 415.
Re: 416
Nowhere in Douglass et al. is there a discussion of consistency of a test statistic. They always use the word in the colloquial sense meaning “does not contradict”. For reference, the other meaning of the word is explained here:
http://en.wikipedia.org/wiki/Consistency_%28statistics%29
I frequently ask “Are the data consistent with my hypothesis?” and it is clear to my audience that I am not talking about almost sure convergence.
You are holding on to that red herring for dear life it seems.
— Sinan
#418—B I N G O !!!!
Craig, 417 “To claim that because some model gives a cooling response there is consistency is to ignore that it is the aggregate model response”
and
Michael, 415&418 If to cherrypick this please for illustration purposes: “the models are not inconsistent with the observations”, that’s one issue. “a large enough standard deviation that one can claim” that, that’s another issue.
So now that leads to something along the lines of:
A) The models are inconsistent because when I combine them and look at the mean the resulting variation created by those differences, I have to create a large standard deviation to fit the actual observations.
B) If I break down models into groups of those that are correct about the surface and those that are correct about the troposphere, I no longer have consistency.
Sounds like the mean is correct for the aggregate.
I’ll ask one more time, and I want the opponents of the Douglass paper to answer me this time, so I know that the answer is something to which they can’t object. What do you think can defensibly be concluded about modeled and observed trends in the tropical troposphere? I just want to make accurate, relatively uncontroversial statements about this issue in the future. Thanks.
Re: #419
Sinan, you nailed it again. I think the counter argument from Beaker has gone from a fatal error in Douglas that reduces the significance of their analysis to something approaching no value to quibbling about the meaning of consistency as he imposes it on the authors.
Part of the trouble here seems to be some confusion about what is an “individual realization”, and what are “averages and statistics”. Let me go back to Dr. Thorpe’s statement to try to clarify this:
Now, an “individual realization” is the particular detailed path that the climate takes to get from time one to time two. It cannot be predicted.
However, according to Dr. Thorpe, the “average and statistics” of the individual realizations is predictable by climate models.
Is a hundred year average of an “individual realization” itself an “individual realization”?
No way. It is one of the “averages and statistics” that Dr. Thorpe says the models can predict. If the hundred year average were an “individual realization”, that would mean (if Dr. Thorpe is correct) that it could not be predicted. Clearly the modelers don’t believe that.
So how about a thirty year trend? Is it an “individual realization”?
Again, no way. It is an average, a long term average, and should thus be predictable by GCMs.
beaker says above that
No. There is not “one realization of the actual trend”, that creature doesn’t exist. The actual trend is not a realization at all. It is a long term average, which (according to Dr. Thorpe) should be similar across individual realizations.
Thus, when beaker and gavin claim that the models shouldn’t be expected to predict the trend because it is an “individual realization”, this is just obfuscation. The trend is not an individual realization, it is a long term average, and as such should be predictable by the GCMs.
w.
beaker #15
Or in other words, for the aggregate to be correct, I have to make the error bars big enough by using the SD to get “a large enough standard deviation that one can claim” that “the models are not inconsistent with the observations”.
Or even put another way, the observations are only consistent with the models when grouping the ones that give two different answers by using standard deviation.
So to make these two groups that “get it right different ways that don’t match” give the same answer as the real world is to get a metric large enough to encompass both sets of results.
Has anyone gotten the SD for the ones matching the surface and the SD for the ones matching the troposphere grouped individually?
425. Willis
So here is my selection criteria. Only select models that have 3 or MORE runs in their
means. Redo your chart with Models 1-12. The models who have run at LEAST 3 runs.
Then apply the beaker test.
Re: #399
Bender the argument to which I referred was the standard deviation versus standard error debate with Beaker. In order to get to that stage of the argument I already noted that assumptions were made, but once made I wanted to be sure that we could agree to how the data had to be viewed in the case of using a SD to compare and SEM to compare and finally which view was more realistic – given the assumptions.
What was being argued was that if one does compare a computer-generated ensemble expectation to an instrumental measurement how should that realistically be done. Arguing that the comparison should not be made is a different argument.
As an aside, I was just thinking that if the authors were truly thinking about inconsistency in a strict statistical sense than surely they would not have used the comparison (more realistic in my view) that they did. That they ignored it because of lack of awareness would further indicate that inconsistency had no statistical meaning to them. They ran a legitimate statistical comparison given the assumptions and a realistic view of the instrumental data being at a different level than the climate model results.
RE 426. Bewyond that SAM you have some model means that are the result of 9 ensemble runs
and some that are the result of one run. It’s apples and gooseberries.
Just to be clear, what I wrote in 418, and tried to illustrate in 415, should not be read as an accusation that the modelers have deliberately sneaked in some models with lower troposphere predictions to “make the standard deviation big enough.” I’m not saying it’s a conspiracy or anything — I assume the modelers work independently in a good faith effort to make the best possible models.
I’d really like to see what Sam asked for in 425 (SD on the two groups independently) or what Steven suggested in 426.
From #368
There’s an assumption in here that models yield random realizations around a stationary mean. I don’t believe that is true, or at least I think it ought not to be true if they really are models of the climate. Repeated samples from a nonstationary process do not converge to SE=0. If a time series process is persistent then the SE grows as a function of n. There are lots of other examples. A Cauchy process (the ratio of 2 std normals) doesn’t converge to a finite variance, or mean for that matter. Repeated model realizations of the tropical tropospheric trend would only converge to a finite trend value with zero associated SE if the models were just simple linear trend+noise machines sharing a common trend value. In other words if the model is just a trend parameter plus random numbers then beaker’s point about the limiting SE is correct.
But then the Douglass test is appropriate. To test whether the model trend parameter is correct, average over the models and use the SD of the mean trend to compare to the observed trend + Std error of the trend in observed data. If they don’t overlap you have the wrong trend parameter in the models.
But if we do not expect the models to have the same trend value, or even to generate the same trend value in repeated runs, then we need to use the distribution of the individual realizations. However there is no guarantee this distribution is stationary, or that the SE declines as n grows. That would need to be established on alternate grounds. In that case the appropriate test is to run a model and assign a probability value to it based on its support in the data, just like in Bayesian Model Averaging. Then you get a weighted average of model runs. And we can all safely conjecture that the models getting the greatest weight would be the ones yielding the smallest tropospheric trend.
#416 beaker:
So you are saying that the correct hypotheses here are: H0: At least one of the models is “consistent” with the data (i.e. is correctly predicting the result), and HA: All of the models are wrong. Boy, you can hide anything behind that one … and you don’t have to identify which one it is. H0 is basically unfalsifiable without enormous amounts of (unavailable) information.
What the climate modellers are trying to show is H0. Ok, that is tough one, but I have seen situations where it was important to convince someone that H0 is true. In particular, bioavailability studies for drugs, a company tries to convince a government agency that their generic version of a name brand drug is absorbed by the body in amounts equal to those absorbed of the name brand medication, ie. to show that the null hypothesis is true. In order to convince the agency of this, they have to show that they have enough information in the study to reject H0 (with a given probability – i.e sufficient power in the test) when the actual absorption differencedifference exceeds a predetermined amount. Without the latter condition, not rejecting H0 is just nonsense and doesn’t qualify as evidence in favor of the drug manufacturer (or in favor of the “consistency” of the climate models).
Presenting the results of a “single run” (was it a single run, or was it chosen from many most of which were not so great – who knows) is certainly not going to put the modellers in danger of inconsistency. The version of the hypothesis of consistency you present (one model run replicates the data reasonably closely – whatever reasonably means) is so unscientific and unstatistical that it just isn’t science.
431 (RomanM)It may be that in this situation, H0 is true, but it certainly isn’t in all situations (by RC’s admission, there are still problems) especially in the area of clouds. But I’m drifting a bit.
I would just like to remind everyone of my very simple request in #422. Still waiting on that. I really want an answer!
mosh 428: Exactly.
Michael 429: I never got that impression that this is anything more than a test of the models with whatever result they have, no conspiracy anything. It’s simply seeing if a mean of two sets (without doing them as separate sets) have a total mean with smaller error bars that match reality. That would tell you if you’re overfitting or not, at least in this case, because of the matching of one or the other but not both. Making them big shows nothing except you can then fit the results. That’s not bagging on the models (or anything) that’s just seeing if as a group they match reality or not.
Excellent question from Willis. If the series is ergodic (which implies that it also needs to be long relative to the error structure) it can be treated as if it were not just a single realization. i.e. This sample statistic describes the realized series just as well it describes the unrealized ensemble. If the series is non-ergodic, then it can NOT be treated as an ensemble statistic and must be assumed to be just a single realization.
Tricky, huh? It all depends on the error structure. Which is what Ross is getting at with non-stationarity in #430. If a series is non-stationary over a given time-scale it must be observed for a very long time before you can quantify the non-stationarity, remove it, and compute the time-series statistics, which you are free now to assume applies to the unrealized ensemble. If the series is non-ergodic, then the non-stationarity will grow without bound. In which case the non-stationarity can never be removed and sample statistics never converge to the ensemble expectation. And in which case classical Fisherian statistics are irrelevant.
Go ask Wegman. It’s true.
How fun is this?
#431 RomanM
Yes. That’s why gavin gloating about being irrefutable is absurd. It’s quite a bad thing to be if you’re a scientist or a hypothesis. Until we have a characteristic AGW fingerprint, it is the hypothesis that can never die even if it were wrong.
Okay, let’s forget about error bars etc. for a second and just look at the data. I have plotted the data (taken directly from Douglass et al.) with observations in blue and models in red (in order to get a good look, two points at 1000 hPa that stand as outliers are essentially omitted). The surface is plotted as 1050.
Now, what do you see here? I guess it depends on what you are looking for. I see a strong tendency toward amplified warming aloft in the models, though it isn’t universal, and no such tendency in the observations. I draw no conclusions from it, except what is visually apparent. Is that okay? Or do I need to add caveats?
Now, If we eliminate models which either over or under predict the surface trend:
It seems one of the outliers survived, but for the most part the mismatch gets worse, I think.
Andrew: something is wrong with your plot. In the data, there are always 3 observed trends lower than all model trends, but in your plot you show model results lower than any data obs at 7 elevations.
nevermind…
438 (Craig Loehle): Really? I’ll have to double check the data, as I think I did it correctly. BTW, I count 5 elevations where that appears to be the case, are you counting some which are due to the thickness of the data points?
re 436 and 437.
Well, I would say that you take the guys who tracked the surface temp better and you
give them more money and use there models as baselines. And no changes to the baseline
unless you prove your change enhances skill.
So you pick your primary Measure of merit, you downselect the models accordingly.
you retire the bad ones, you improve the good ones.
441 (steven mosher): I’m just testing an idea I had as to what would happen if I used models with surface trends that weren’t to high or low, I would say this makes the models better than the others, since the could be getting possibly erroneous surface data right for the wrong reasons. So I don’t take this as my “measure of merit” (it’s actually the modelers who argue that their models are good becuase they reproduce the GMST). Anyway, you can’t decide which models are good or bad on the basis of the tropics alone, but by looking at all areas. If the “best” models in the tropics are terrible in most other places, then they aren’t really better. But I’m sure you already know all this.
Someone suggested that we should actually look at the confidence intervals. Since the question is the change in trends relative to the surface, I have set this up the same way as my plot above, with all the data and models set to match the surface (as above, the two datasets with no surface values are left untouched, it doesn’t change the results).
Here’s the plot:
As you can see, all of the datasets are outside the 95% confidence intervals of the models …
bender, thanks for the clear explanation of the issues above. I suspect that this particular measure doesn’t change a whole lot over time, either from run to run of a single model, or between models. I say this for a couple of reasons.
The first is the good agreement between almost all of the models (save a couple of mutants).
The second is that the phenomenon is predicted by theory.
Because of that, my best guess is that the trend ratios are ergodic … but YMMV.
w.
443 (Willis Eschenbach): Douglass has apparently written in with comments, and he advises against normalizing the surface trends.
http://www.climateaudit.org/?p=3058
beaker,
Doulass et al made it very clear what they meant by “inconsistent”. You say they did not.
Can you please explain what is “wrong” with the following exerpts from the paper.
The other problem I have with the dismissal of the paper by Gavin and yourself is that you have deliberately gone back to a statistical discussion of the range of the models when you know that the paper specifically avoided doing that (and for very good reason).
It bothers me that varying number of simulations were run for the different models.
Could it be they repeated the simulations until they came up with an acceptable average figure for each of the various elevations?
What other reason would there be to run a simulation nine times in one case and only once in some of the others?
Morning all.
Marine_Shale #446: Previously on this thread I was accused of making up statistical definitions of “inconsistent” and “bias”, but I was able to show that both of these terms had specific statistical connotations commonly understood in this context. If Douglass et al. have defined their own meanings of existing statistical concepts, that are greatly at odds with their established use, it is hardly a surprise that their findings are misunderstood. Especially if you just say, the models are inconsistent, the data cannot be reconciled with the model, without discussing what they mean by these terms, the obvious interpretation is a much bigger claim than their statistical test establishes.
RomanM #431:
That is the test for inconsistency, which is what Douglass et al actually claimed. As I said, the reason inconsistency is such a big claim is exactly because it is such a low hurdle! I have already said that consistency is not the same as usefulness, so I am not saying that if the models are consistent then they are correct, far from it.
Ross McKitrick #430: For the SE of the trend not to tend to zero as n increases would require the standard deviation of the ensemble to diverge faster than sqrt(n). I can’t see how this could happen as the models are constrained by their underlying physical assumptions from giving essenitally infinite estimates of the trend that would be required for that to happen.
Sam Urbinto #425: You can’t make the error bars bigger. The error bars are decided by the variability of the ensemble predictions.
Andrew 422: From the results of Douglass et al. I would conclude that the models are biased, i.e. on average they significantly over predict the observed trend. However they are not inconsistent as the observed data are within the range of values considered (barely) plausible by the models. One thing I would definitely conclude is that climatologists shouldn’t be making strong statements based only on the mean of an ensemble. If they are not giving error bars based on the spread of the ensemble, they are ignoring much of what the ensemble is telling them.
Sam Urbinto #421: How many times have I got to say this, inconsistency is nothing to do with whether the data lie close to the mean. Inconsistency is about plausibility, which means it is about the error bars for the distribution as a whole, not just for the mean. I am also getting quite worried by the idea being discussed here that the error bars are “created”, that is deeply wrong from a statistical perspective.
There is a new thread on this specific topic, so I’ll move over to that one now.
#398: That was helpful in explaining your viewpoint. However, doesn’t it still leave the question regarding invalid models that find their way into the ensemble? It appears that one could add any given model to the ensemble to keep observational data within the mean with the tradeoff being worse predictive accuracy (larger error bars on the predictions). At what point does the scientific community say that this inaccuracy is too large to find the models useful as predictors of climate?
Secondly, aren’t these models supposed to predict from proven physical principles? How could they be so wrong on a hindcast?
Maybe it can’t happen in the current suite of models. But what if those models are wrong? What if this is the way the actual climate system’s “internal variability” functions, and it is therefore the way that the models ought to function, if only their “internal climate variability” was modeled correctly.
It is important to distinguish between the physics of GHG forcing and the physics of the stochastic component. The alarmists are trying to attribute the post 1970s GMT trend to GHGs. The skeptics are trying to attribute it to persistent stochasticity.
You say you “can’t see how this could happen”. Are you sure you have opened your mind as to the possible ways that variability might grow as the internal climate variability reveals itself to us? Remember: we have not been studying GMT in detail for more than 5-10 decades. That’s not very much time in the slow-motion world of ocean dynamics. Ocean tempeatures. Slow vertical mixing. Now can you see?
449 (bender):
Your generalization doesn’t fly. Some skeptics attribute the post 1970s trend to external forcings (I know Pat Michaels, for one, thinks it is anthropogenic) others to solar forcing (becuase of course some of it could be, if ACRIM is correct or at least is a good representation of the sun’s effect) and some to internal variability. I won’t reiterate my additive model here, since it bothers you when I do so.
Re: #447
Beaker, I truly believe that all the thinking people participating in this thread are well aware of your approach to downplaying the import of the Douglas article. Martin Shale and others here have pointed to what the authors clearly meant by their analysis with the given the assumptions. Their analysis shows realistically that the ratios of the tropospheric to surface temperature trends in the tropics as derived by the mean of ensemble of models and compared to the instrumental data are different with a low probability that that difference occurred by chance.
Given all the counter evidence, I am beginning to wonder why you continue to concentrate on the word consistency and associate the discovery of that word in the paper as somehow negating what the authors were purposely and clearly analyzing. Is that normal? And you can take that last word in the general or statistical sense?
#15 “This made the error bars about four times narrower than they should have been.”
#447 “You can’t make the error bars bigger.”
Ah, so you can make them more narrow, but you can’t make them bigger. I understand perfectly now.
#450
Go ahead. It’s wrong. But go ahead if you like.
#451
It’s called saving face by constraining the debate to ensure a narrow, winnable argument. And hope no one notices the dodge.
Beaker’s anal insistence on distinguishing between “consistency” and “bias” when the two words can be taken to mean the same thing is a waste of bandwitdh. Models that are “consistent” with observations have zero “bias”. Models that are “biased” so badly as to be “inconsistent” with observations are, umm, “incorrect”. “Back to the drawing board” is another very scientific way of putting it.
beaker must quit the word parsing and answer the real questions if he wants to save face with this crowd.
453 (bender): Better yet, how about you explain to me what I can do to improve it? It certainly doesn’t help to insist on one variable explain everything-but there is no way to express all the complex interactions in the system, so the additive model is the easiest way for me to convey what I believe is important for climate. But I don’t know why you didn’;t just ignore my little snipe at you there given how immaterial it was.
I don’t think you are being fair to beaker at all, but given that I never seem to win arguments with you, I won’t get into this tussle either…
#454 For a guy who says on another thread that he doesn’t like squabbling …
Andrew, just for you I’m collecting a list of ill-posed arguments based on additive models that posit that the circulatory modes are independent of GHG AGW. Lucia has spotted these junk arguments and so have I. They are the pure skeptic’s new drug: “it’s not a trend, it’s just PDO”. That ain’t the way it works. Heating from GHGs gets whisked into the AO circulation. It doesn’t float around in a separate layer of the atmosphere waiting for you to measure it.
I think that’s the mistaken argument Ron Cram is about to make on another thread.
re Andrew # 450:
Of course there are other skeptics that just don’t think we understand it well enough yet to model correctly, and to make forecasts about how much hotter it’s going to be by 2100.
What is the physical interpretation of the tropical troposphere observations?
My conjecture thinks of the tropical tropsphere as heterogeneous, composed mainly of
1. relatively small regions of moist, warm rising air (the thunderstorms of the Indo-Pacific Warm Pool and ITCZ) and
2. relatively large regions of upper air (outflow from the thunderstorms) that are raditionally cooling and sinking
The temperature profile in the thunderstorm region is probably behaving pretty much as expected, driven by heat and mositure from the near-surface layer.
The temperature profile in the radiationally cooling regions may not be behaving as expected, perhaps radiating more IR into outer space than the models assume. Lower humidity (water vapor content) than the models expected could account for that.
And that is an important issue, because (as I understand it) the CO2 sensitivity of the models is largely driven by increased water vapor in the upper troposphere (UT). If UT water vapor is not behaving as expected (due to incorrect assumptions about cloud and precipitation?) then the sensitivity may be wrong. That would have a game-set-match kind of impact on the most dire AGW concerns, in my opinion.
#457
Interesting. Hopefully some of the physicists will read this and comment.
455 (bender): I’ve probably seen it more often than you have, actually. Spencer, Lubos, Easterbrook, D’Aleo, Taylor, and on and on. I’ve told you before that you really out to ask RC if they’ll let you do a post to put the PDO myth to rest-it’s quite pervasive!
bender,
I tried earlier to more or less continue Judith Curry’s comment about deep convection parameterization and why the GCM’s in general predict faster warming in the troposphere, but it got moved to Unthreaded and has died there. I think it’s totally relevant to this thread, but I’m not the boss.
457 (David Smith):
My take on the Douglass paper is that it relates to the humidity calculations in the models. The atmosphere could respond to CO2 forcing by maintaining constant relative humidity (atmosphere grows wetter) or constant absolute humidity (moisture in atmosphere stays the same, any excess from GW rains out). If the modelers’ claim of potentiation of AGW by water vapor is correct, the atmosphere will grow wetter. Since the dry adiabatic lapse rate is -1.0 deg C per 100 m and the wet adiabatic lapse rate is -0.6 deg C per 100 m, an increase in atmosphere moisture will cause a decrease in lapse rate, and temperatures aloft will increase more than surface temperatures.
Since this is not observed, the lapse rate is not changing, which implies that the moisture content of the atmosphere is not changing, which implies no positive feedback on surface temperatures from water vapor.
A better example with Beaker’s heigth would be like this. I will set the analogies in brackets.
The scientists task is to guess Beaker’s future heigth (earth’s future surface temperature), when adult (in 50 years time). Beaker is now only 11 years old, and his actual heigth is well known to be 4’8″ so far (earth’s recent surface temperature).
The scientists have carefully studied the human race (earth’s climate history) and, based on their knowledge, make a prediction on Beaker’s growth process that is backwards-consistent with the growth he has experienced so far (actual temperature trends) and with his actual heigth. Because their models for human growth matches Beaker’s heigth so far so perfectly, they claim that their models are good.
However there is a problem. Their models correctly say that Beaker’s heigth right now is 4’8″, but they count on the fact that a typical male human must have not passed puberty at the age of 11 (tropical tropospheric temperatures must be higher than surface temperatures), so a great rise in Beaker’s growth rate is expected later on (warming by emisions from the warmer troposphere are expected to heat the surface). But the real data, and one which is perfectly known by the scientists too, is that this particular male human that Beaker is HAS ALREADY passed puberty at the age of 11 (the tropical tropospheric temperatures are NOT higher).
Now, the scientists can argue, and they will be right, that some of their model realisations had also passed puberty at the age of 11 (did not show bigger warming for the tropical troposphere), so Beaker’s personal condition regarding puberty (tropospheric temperatures) does not invalidate their models. Fine.
On the other hand, we are also right to claim that, in order to make a future prediction of Beaker’s heigth (earth surface’s temperature), we should only rely on the few realisations that showed an early puberty (tropical troposphere’s little warming), and at the same time, show a 4’8″ heigth at the age of 11 (actual surface temperature), because that is what the real case shows, no matter how strange it looks, it is OUR case, the case that matters, the case whose future we want to predict.
If there is ONE model realisation that correctly shows an early puberty (low tropospheric warming) and a heigth of 4’8″ (today’s surface temperature), I want to know what future THAT realisation predicts for Beaker’s heigth. The rest of the realisations are unimportant to me, and I will in no way trust their predictions because they don’t even match reality.
And if there is no single realisation in the models that show Beaker’s actual conditions regarding height and puberty status (surface and tropospheric temperatures), then I will have to say that the models are not good enough and I cannot make predictions on Beaker’s future heigth (future surface temperature) based on them. Because high tropospheric temperatures are a MUST-BE condition for later surface warming in the GH theory, in the same way that not having passed puberty is a MUST-BE for expecting a big increase in heigth later on for a male human.
With my traning in chemical engineering, I’m wondering if the climate is behaving like a distillation column. Like adding more steam (i.e., heat) to a reboiler, GG’s absorbed more of the heat that would have been lost to space. In a distillation column, when more steam is sent to the reboiler (i.e., a heat exchanger at the bottom of the tower), then more liquid is vaporized and sent up the tower. If unchecked, more of the higher boiling component (think water and ethanol as the two main components inside the tower) is sent up the tower. Eventually, the purity of the ethanol going overhead as the distillate decreases as the concentration of water increases (not good!). So, how does one compensate if steam to the reboiler (i.e., the source of heat to the system) cannot be cut back? Easy, you send some the condensed overhead stream (called reflux) back down the tower as a liquid to cool it down. So, if more heat is being redirected back to the earth’s surface due to GG’s, then it appears to me that the atmosphere over the oceans (such as in the SH) causes more water to be vaporized. But instead of producing a positive feedback, it condenses at some altitude as it is loses heat. Eventually, this heat finds its way out to space. If all this happens very fast (i.e., it’s in equilibrium), I don’t see how “climate sensitivity” occurs.
So, to continue the analogy, the incoming irradiance plus the additional heat from GG absorption is like the steam to the reboiler, and the coldness of outer space is the overhead condenser. When more heat is applied (via GG’s), all that means is more vaporization and condensation going on between the earth’s surface and outer space. This is exactly what happens in a tower when more steam and reflux is added. There is more vapor traffic up the tower due to additional heat added to the reboiler, and when distillate is sent down the tower to compensate, there is more liquid traffic going down the tower. Overall, this does tend to increase the temperature at the bottom of the tower (or the earth’s surface, if you will) and lower the temperature at the top of the tower (or the stratosphere, if you will). However, both temperatures reach a plateau. The temperature does not runaway. In the example above, the overhead and bottoms temperature of the distallation tower reach their respective boiling points at the pressure of the tower. So, if the tower was run at atmospheric pressure, the bottoms stream can never exceed 212 F (the bp of pure water) and the top stream can never exceed 176 F (the bp of the ethanol-water azeoptrope, if I recall).
Maybe this is why we are seeing no temperature increases across the SH (mostly covered by oceans), and the highest temperature increases across the NH, particularly Asia (the largest land mass of all). In essence, there is not enough moisture to carry the heat into the atmosphere where it can “lose” it (via condensation) at higher altitudes. I guess the important point here is convection. It’s convection that carries heat up the distillation tower.
463 Chris
Interesting post.
Of course, in the atmosphere, there is another parallel negative feedback process; cloud formation. It is as if some of your excess water was also fed back to the heater in order to reduce the supply of steam.
nylo: Just a rhetorical question. What if I have 22 models who’s mean is within 2 SD of beaker’s height when taken as an ensamble? Even if we know a tire alone can’t get us to 80 KPH, when I put it together with everything else as an ensamble it can. 🙂
I think this makes a lot of sense (Pochas, Chris, Pat), taking water and the lapse rate into account in the atmosphere as the key.
The lapse rate wet/dry is something I mentioned in another thread about models and the troposhere.
Also I put up some bits and pieces from an online oceanography book at Texas A&M, among them
And
To which I added (in the post) that I would contend that putting heat into the atmosphere anywhere is the same thing as putting it anywhere / everywhere; it is the atmosphere after all. But that’s somewhat reconciled if you define “global warming” as only warming directly due to GHG as I think they are (I don’t agree exactly, but at least they didn’t make the mistake of saying UHI is only local and covers “such a small area of the planet”).) But it’s obvious the cities and their heat have an affect upon the weather.
The Urban Heat Island Effect And Its Influence On Summer Precipitation In The City And Surrounding Area
All of chapter 7 of The Global Climate System: Patterns, Processes, and Teleconnections is on urban impacts on climate) 7.4 is on wind, cloud cover and pressure and 7.6 is on moisture and precipitation.
Don’t even get me started on waste heat, farms, suburbs, freeways and the difference between the N and S hemispheres…. 🙂
Sam: Actually, in my example, Beaker’s heigth so far is correctly predicted, and represents the surface temperature increase we have experienced so far.
The models would be consistent with the growth history of Beaker, but would get the causes completely wrong, invalidating their predictions for the future. They would think that Beaker’s greater than average heigth is due to having been treated with extra hormones, they would predict a very tall Beaker in the future, and they would disregard Beaker’s early puberty as unimportant. The truth would be that Beaker would have quickly become tolerant to the extra hormones, and the reason for him being taller than average would be his early puberty, which causes a quick growth, but with the drawbacks of almost stopping any growth after it finishes.
Beaker’s early puberty would fall within the 2 SD limits of the models predictions for the age of puberty of a male human. But the particular cases or realisations that make such a limit exist for the models never predicted a tall Beaker later on. What I am saying is that, if every model that shows an early puberty doesn’t predict a tall person, then that is an important fact in order to consider predictions more or less likely to become true. In the same way, if every model that doesn’t show much warming in the troposphere also doesn’t predict a big warming on earth surface for the future, then that is very important in order to consider the predictions more or less likely to become true.
#24 — mzed, “. If it’s so easy to make a GCM that shows global *cooling*, for example, why hasn’t anyone made one?”
Take a look at D. A. Stainforth, ea (2005) “Uncertainty in predictions of the climate response to rising levels of greenhouse gases” Nature 433,403-406. These are the ClimatePrediction.net folks. Figure 1a of that paper shows that nearly half of their 2,017 simulations of doubled CO2 produced a cooling climate. These simulations were systematically rejected by the handy judgment of being physically unreasonable. Everyone knows, after all, that doubled CO2 produces warming. This kind of result pruning lacks statistical integrity and makes the conclusions entirely unreliable. Nature and its reviewers didn’t see it that way, big surprise.
Perhaps a good rule of thumb is to not judge the range of output trends of GCMs by what is published. We rarely get to see the complete set of projections; just the physically reasonable ones.
Re: Pat Frank (#28),
They start with 2,017 unique simulations and use only 1,148 of them? Do I have that right?
#45: are you really trying to claim that no scientist ever re-runs an experiment based on undesirable results?
You’re looking at the Stainforth paper like it’s a laboratory experiment. But it’s not–as the authors themselves state, their article describes an “ensemble of ensembles”. They’re doing an analysis of other experiments (the 2000+ simulations). If they re-ran their “experiment” using different a priori assumptions, all they would do is end up with the same results they have now.
Now, I agree it would be more interesting if they went back to each simulation they threw out, and looked at their a priori assumptions, re-ran each simulation, then plugged it back into their analysis. That would be much more proper. But that’s probably not feasible, at least not right away–look at this paper as a good first step, in a process that can be improved upon. Climateprediction.net, after all, is still up and running!
Re: mzed (#49),
Hunh? No.
It is an “experiment” done in a computer “lab”. They even refer to these runs as “experiments”. So what’s your beef? My point is that the Stainforth paper potentially contains a huge bias. I am right. My job is finished. Auditors are not experimenters.
I would agree that the runs are laboratory experiments; but I would also argue that the paper itself is not–they themselves call it an “analysis” and note that the “Individual simulations are carried out using idle processing capacity on personal computers volunteered by members of the general public”. Here, the volunteers are the lab techs, and the laboratory is spread across the world. Anyway, I am agreeing with you; I would just characterize it differently. The authors of the paper can’t get rid of the bias by doing anything differently themselves; all they can do is ask the lab techs to re-run the experiment(s). Which they are currently doing. So we agree; we just have different perspectives on it.
Re: mzed (#51), The paper can not be relied upon. Yet it is published in Nature. And it is, in fact, being relied upon. Little wonder we differ in our opinions.
#34 — bender, you’re correct. And then 6 of the remaining 1,148 also showed cooling during doubled CO2 and were taken out of the experiment. The paper predicted up to 11.5 C of warming by 2100, and this number still gets cited as a real possibility, as Tapio Schneider did in his recent Skeptic article.
Re: Pat Frank (#53), How do you remove the cool runs on the basis of the “simplified ocean” if the very same “simplified ocean” is present in all runs? Wow.
Got another one for the database:
A “simplified ocean” is a good thing if it produces warming, bad thing if it produces cooling.
Re: Pat Frank (#475),
This statement makes me wonder:
First, my understanding is the control period is where forcings are held constant and the only variability is weather noise. Excluding any run with a 8 year trend that exceeds 2 deg/century means the modellers are assuming that weather noise cannot produce trends larger than that on their own. This strikes me as a rather large assumption and I wonder if it has any scientific basis.
Second, modellers seem to feel that a 8 period is long enough to conclude that a run is unstable yet they insist that an 8 year trend in real world weather data tells us nothing about how the models are doing. An interesting contradiction.
Re: Raven (#479),
A model is not the climate, as people keep saying here. If a model is not working, it could take only a year or less to see it has a major problem. If you look at the known temperature record, there are similar or longer periods of time where the temperature has dropped, then resumed it’s climb up again.
Re: bugs (#480), I don’t see your point wrt Raven’s. It is my understanding that it is a run(s) that is not working, not the model as in Bender’s post 474, 476, and Frank’s 475. Which (runs) is what Raven states in 479. I would say that this also needs to go in Bender’s database “When is eight years enough, or not enough? When the conclusion produces the support we want.”
Re: John F. Pittman (#482),
Is bender a mind reader? He could make a fortune with such superpowers.
#42 — mzed, I did read their supplemental information. The same caveats applied to the models used to reject the runs showing cooling can just as well be applied to those that showed warming. The model is the same throughout, and so the model inadequacies are the same throughout. If the model inadequacies are sufficient to reject results they didn’t like, then the same inadequacies vitiate the results they kept. The judgment of model instability is based subjectively on the content of the result.
Bender’s comment in #469 is definitive. The criteria must be set up before hand, and not adjusted on the fly in order to make the results come out right. The whole paper is a poor charade of science. Peer reviewed by, and published in, Nature(London).
#476 — The $64,000 question, bender.
“There’s that word uncertainty used once again in the same sentence with climate models — and again not by a skeptic/denier.”
Of course the models are uncertain, that is why there is ongoing and intensive development of them. The new generation of hardware will allow much better modeling of clouds, for example.
6 Trackbacks
[…] caution (due to their lack of correspondence in reality). However, as Boris states insightfully on CA and lucia liljegren’s blog If the Douglass analysis is correct and the tropical troposphere […]
[…] http://www.climateaudit.org/?p=3048 […]
[…] unknown wrote an interesting post today onHere’s a quick excerpt205 (Willis Eschenbach): I “hate” to be pedantic, but a trend is almost never exactly zero. 207 (Paul Biggs): I could argue for lower, but I’m not sure how good I’d be at defending such an estimate. All this talk of error bars, … […]
[…] erik wrote an interesting post today onHere’s a quick excerpt#207. But Paul, what about the MODELS. Don’t they count as proof??? /sarc off. […]
[…] beaker wrote an interesting post today onHere’s a quick excerptRe: 379. Nope. Models can be wrong in infinitely many ways but correct in only one way. That is, under the null, we can calculate the conditional probability of models generating something that is as far away from the observed that as … […]
[…] Steve McIntyre wrote an interesting post today onHere’s a quick excerptBeaker: further on test for outliers. We have a mean and variance for heights of a population A and a sample of 4 professional basketball players. The test for outliers would consider that the 4 sampled heights could be above and below … […]