Continuation of Koutsoyiannis et al 2008: On the credibility of climate predictions.
-
Tip Jar
-
Pages
-
Categories
-
Articles
-
Blogroll
- Accuweather Blogs
- Andrew Revkin
- Anthony Watts
- Bishop Hill
- Bob Tisdale
- Dan Hughes
- David Stockwell
- Icecap
- Idsos
- James Annan
- Jeff Id
- Josh Halpern
- Judith Curry
- Keith Kloor
- Klimazweibel
- Lubos Motl
- Lucia's Blackboard
- Matt Briggs
- NASA GISS
- Nature Blogs
- RealClimate
- Roger Pielke Jr
- Roger Pielke Sr
- Roman M
- Science of Doom
- Tamino
- Warwick Hughes
- Watts Up With That
- William Connolley
- WordPress.com
- World Climate Report
-
Favorite posts
-
Links
-
Weblogs and resources
-
Archives




171 Comments
To do a cross-post link, best for the moment to just use the number, or save the link hiding under the comment number (i.e. right click on the comment number and use “Copy Link Location” or equivalent.
I’ll see if I can find a way to improve on that.
Dear all, also Kenneth #530, and Bender #531
I would like to emphasize a fundamental issue about the implications of LTP, which has been reiterated by Dr.K. in many of his papers. Almost all statistics calculated from samples of LTP processes would be so much affected (sometimes severely) that many classical statistical procedures/tests (including regression, trend testing, cross/auto-correlation testing, parameter estimation, quantile estimation, confidence intervals …) would give misleading results. As one example, Dr.K’s work has inspired a paper on trend testing that I authored [Hamed, K. H. (2008), Trend detection in hydrologic data: The Mann–Kendall trend test under the scaling hypothesis, J. Hydrol., 349 (3-4), 350-363]. I am also currently writing a paper on the significance of cross correlation under scaling, with similar conclusions. The point is that many classical statistical methods, including some of those used in everyday analysis, just do not recognize/account for the effects of LTP. As such, there is no point in trying to use classical statistics to question LTP (this would be like using classical mechanics to question relativity). For example, if you fit a trend line to a time series, you have already made up your mind. Chances are you will get rid of most LTP (unless you have a very long time series) and end up with a nice iid/STP series plus a “significant!” trend (you have already decided it was significant the moment you fitted that trend line!) Unfortunately, it goes also the other way. Under LTP, the larger uncertainty would make it harder to distinguish weak real trends from LTP behavior, which is our fundamental problem. In other words, the iid/STP “glasses” are too focused to see LTP, while the LTP “glasses” are too hazy to see weak trends if they do exist (so in that respect, LTP is not a blessing! Or is it?) Note that LTP does not completely rule out the existence of a real weak trend, it simply “neutralizes/deflates/downgrades” apparently strong statistical inferences such as “unprecedented,” “with very high confidence,” “highly significant,” and “overwhelming evidence,” pending more information (longer time series), simply because of the higher uncertainty under LTP.
Although iid/STP plus significant trend(s?) would make our lives much easier (or would it?), if LTP is nature’s way, ignoring it will certainly not. The fundamental problem IMHO is whether LTP can be sufficiently supported (or otherwise dismissed) using some impartial fundamental tool (entropy?) That is why I really enjoyed Dr. K’s paper(s) and the discussions in this thread very much. Thank you Dr.K and all.
K. Hamed (#2):
Thank you for the interesting and thoughtful comments.
Just to clarify the issue (for me), when you note that
are you suggesting that the concept of a real weak trend is well defined? I ask in part because DrK has questioned whether we even know what trend means in the presence of LTP — a paradoxical observation that I have not been able either to resolve or dismiss.
Would you agree — and perhaps this is your point (if so, I apologize for being dense) — that there is no currently accepted (i.e. rigorous and consistent) statistical method for separating trend from LTP for systems known to exhibit substantial LTP? If so, what does this imply?
Again, thank you for the interesting comments.
Following TAC # 3, is there likewise a method for prediction of the (discussed) LTP effect following an anomalous high or low event, a spike like a hurricane or a large volcanic eruption for example, that might seem to happen at random times? Is a spike a required event to initiate a new trend? Or does it do nothing at all? How do you incorporate a large spike into a real weak trend, mathematically, with confidence? Is there a case to separate trends to periods between spikes?
Until now I had thought that LTP was a trend by definition. I also thought that a spike was the inevitable proof of model failure to forecast in the long term. (See CSIRO Drought & Exceptional Circumstances Report & Dr Stockwell’s work). Now I do not know if semantics are being stretched or if progress is being made.
TAC (#3)
For your first good point: as far as I remember, Dr.K questions the meaning of trends only when the are solely inferred from the observed data. There are time series which exhibit trends for known physical reasons (urbanization of a watershed, ….). So I guess the paradox arises only if a trend cannot be physically justified, at least partially.
For your second good point: I think that by accomodating LTP in statistical methods we do have a rigourus and consistent statistical methods to distinguish LTP from trend. The problem is that the power of all statistical tests (including the ones that accomodate LTP) depend on the length of the time series. With the added uncertainty introduced by LTP we simply need much longer sequences than under STP.
I need to ask Dr.K. and the others this related question: shouldn’t we be more concerned about (or at least have the added concern of) LTP fluctuations than trends? after all, LTP fluctuations may be as large, but the direction is not predictable.
1. As I understood Gavin Schmidt’s critique of the 2007 paper, one can’t make a significant test of the GCMs out of data from only a few locations. I assume he would say the same thing about this paper. [Of course, if we were to include all available monthly data (as lucia has done), the response is that the models are not really falsifiable at all.] The authors discuss the notion of falsifiability which makes me wonder if there is not an apples and oranges problem because it is not clear what empirical claim(s) the models actually make.
2. Is there any standard by which a set of data can be deemed regionally representative rather than an outlier? I note that the 3 North American data sets used in the paper show a very warm period in the 1930s and a far less dramatic rise in the 1990s which seems somewhat heretical. How hard would it be to find a data set of the same sample size and with a comparable global range that statistically conforms to the AR4? Is there such a data set?
I realize that if LTP can be shown to be the operating principle in climate (temperatures) then all bets are off using the classical approach for statistical analysis of temperature (linear) trends. What I wanted to do here in my own simple-minded approach was to look at the trends in global temperatures using the GISS data as divided by regimes that can be justified with statistical treatments but not associated with any causes for those regime changes. The breakpoints associated with regime changes in global temperatures can be found in “ABRUPT GLOBAL TEMPERATURE CHANGE AND THE INSTRUMENTAL RECORD”, by Matthew J. Menne at the NOAA National Climatic Data Center, Asheville, North Carolina linked below:
Click to access 100694.pdf
Menne list several versions of breakpoints derived by different calculations. I suspect my further calculations for these sub-periods would not change significantly by using any of the breakpoint methods. I choose the ones established by Karl, as those points gave nearly equal partitions and eliminated any shorter periods that could effect the statistical significance.
Below I compare the mean anomaly temperature regimes for anomaly trend, r (AR1) for autocorrelation of the trend residuals and p (fit) of the probability for the chi square goodness of fit to a normal distribution of the residuals. I use the GISS global annual mean anomaly temperature series and Karl’s breakpoints at 1910, 1945 and 1975. The GISS data can be linked to: http://data.giss.nasa.gov/gistemp .
Below I listed the calculations for the four climate regimes:
1880-2007:
Trend = 0.60 degrees C per century; r (AR1) = 0.58; p (fit) = 0.37
1880-1909:
Trend = -0.34 degrees C per century; r (AR1) = 0.30; p (fit) = 0.96
1910-1944:
Trend = 1.12 degrees C per century; r (AR1) = 0.14; p (fit) = 0.95
1945-1974:
Trend = -0.07 degrees C per century; r (AR1) = 0.19; p (fit) = 0.95
1975-2007:
Trend = 2.11 degrees C per century; r (AR1) = 0.07; p (fit) = 0.96
I am proposing here that looking at long term trends in temperature series creates problems with autocorrelation and departures from normality that are significantly reduced when partitioning the series into statistically determined regimes, albeit without attribution to a basis for the regimes and changes of regimes.
I also have some reservations about using the fewer data points in the sub series to, not so much fail to reject the null hypothesis that the data fits a normal distribution, but to show very high p values as evidence of an excellent fit for a normal distribution becuase in my mind with fewer data the binning choices for the data for the chi square test become more critical. In other words, I think the results show excellent fits, but that with more data those fits may be merely good.
Dr. H and Dr. TAC, thanks for this enlightening discussion. Indeed, we must question whether we even know what trend means in the presence of LTP and, indeed, if we have physical reasons that can induce a change, the situation in formulating and testing a statistical hypothesis makes more sense. The “weak trend” problem reported by Dr. H may be not so important and perhaps artificial. Why should a statistical method detect something that is “weak” (in comparison to natural variability) and perhaps not well defined? And what would be the real gain from this detection? Classical statistics cannot detect “weak” changes either. The difference is that with LTP the natural variability is larger than in classical statistics and thus our perception of “strong” and “weak” changes. Statistical approaches are good to detect significant changes, not weak details. Dr. H’s excellent paper provides easy means for detecting such statistically significant changes (not necessarily trends of pre-specified form because the test is not parametric) under the presence of LTP.
I have a question. Would the geological record of the last four ice ages be considered a LTP by the statistical methods we are discussing here?
EJ (#9),
I’ll answer a slightly different question: If one simulates global temperatures using an LTP model, it is easy to obtain (synthetic) “geological records” that include frequent and persistent ice ages — just like the real geological record. With only STP (i.e. ARMA error structures), you generally do not see ice ages unless you include (unrealistic, generally) causal factors.
In some sense, LTP “explains” the ice ages as a manifestation of natural variability.
Of course, many questions remain unanswered: What causes LTP? Why do large natural systems exhibit LTP? etc.
And the implications of LTP, from both a scientific and public policy perspective, may not be welcome…by anyone.
Thanks Dr. TAC,
Natural cyles. Studying the natural sciences it is amazing to see the vast amount of relationships that are cyclical, especially with respect to time.
I have to wonder, why would the cyclical nature of a phenomenon be foriegn to any natural scientist, especially when studying and trying to model climate?
This venture into LTP analysis appears to be obviously valid, and apparently long overdue.
Thanks again to everyone for this forum, intelligent discussion and cutting the sharp edge.
Once you start this, then you have to start applying weights and cycles to particular LTP’s, no?
Gotta love it, this settled science.
EJ,
had to try with the simple model I used in http://www.climateaudit.org/?p=3361#comment-292113 , this one seems to be too simple to generate short interglacials ( wrt. glacials )
“Strong trends” can kick out simple LTP models (for example, if temperatures get lot higher than upper prediction interval of the picture linked), AGW can coexist with LTP natural variability. But with LTP those silly CIs of AR4 Table 3.2. has to be deleted.
EJ (#12),
I am not sure I understand what you mean. LTP time series typically include a lot of interesting structures; while you could add “weights and cycles,” I am not sure they are needed.
If you are comfortable playing with R, it is worth taking the time to simulate some time series — see what they really look like. It’s easy. For example:
library(fracdiff)
fdplot<-function(
npts = 1000,
d = 0.4,
ar = 0.8,
f = 0.1
)
{
y <- fracdiff.sim(n=npts,d=d,ar=ar)$series
ylim <- range(y)
plot(y,ylim=ylim)
par(new=T)
plot(lowess(y,f=f),ylim=ylim,col=’red’,type=’l’)
}
Set the seed on your random number generator so you can reproduce things if you want:
set.seed(123457)
Then generate some — dozens to hundreds — of realizations with
fdplot()
fdplot()
…
This exercise should provide a good sense for what LTP series look like.
The default values of npts, d, and ar were chosen because n=1000 corresponds to the infamous last millennium, d=.4 corresponds to what you see in many hydroclimatological records (although d=0.46 to d=0.49 are not unheard of), and ar=.8 is just a nice number.
Explore other cases, too, including longer records, different values of d (particularly the approximate (fracdiff.sim balks with ar=0) “white noise” process:
fdplot(d=0,ar=0.001)
)
Note that these models are all stationary for the parameter values considered here (0 .le. d .lt. 0.5 and 0 .le. ar .lt. 1).
Enjoy!
🙂
#15, If I’m not completely lost, half-integration is ARFIMA(0,0.5,0), the one used in the above figure. And this ties those who are interested in predicting stock returns with those who are interested in accuracy of clocks (*)
(*) See Barnes and Allan, A Statistical Model of Flicker Noise,
Proceedings of the IEEE, Feb. 1966 Volume: 54, Issue: 2
Further to Dr. TAC’s comment (#15) and EJ(#11 and #12)
These figures show how Fractional Gaussian noise can reproduce the behavior of natural data (the Nile flow and stage in this case). Though not necessarily THE model for natural data, apparent Trends/jumps/cycles/spikes come for free with this single parameter model! Get yours while supplies last.
[ed: K.H., for some reason your IP address was blacklisted. Pulled your posting out of the spam pile :)]
RE my previous post (#16) Many thanks to admin:)
Actually it is a three-parameter model (counting the mean and variance of course). Sorry for the last sentence, it seemed to go well with the one before it at the time :).
If we go to time scales of many millenia (in order to reproduce the glacial periods), it may be wise to use also some periodic components to represent the Milankovitch cycles in a more explicit manner. In Fig. 18 of the paper ‘A toy model of climatic variability with scaling behaviour’, Journal of Hydrology, 322, 25–48, 2006 (http://dx.doi.org/10.1016/j.jhydrol.2005.02.030; preprint in http://www.itia.ntua.gr/en/docinfo/864) you can see a simplistic example. The model used is one harmonic with period about 100 000 years plus a time series with LTP. For demonstration purposes, the latter series was produced by a deterministic chaotic model, without any random component (no random generator at all), as specified in the paper. This deterministic model, by appropriate choice of parameters can produce series exhibiting LTP. Notice that the entire model is ‘a toy model’ to play with and perhaps acquire some understanding on the emergence of LTP. It is not a real climate model. But you can see in Fig. 18 that it can very well reproduce 400 000 years of the Vostok climate. 🙂
Sorry for the anagram: The link to the preprint is http://www.itia.ntua.gr/en/docinfo/648
TAC, when you say:
Is there any chance that you can display or link some examples of simulated plots? Is not a 1000 data points too few to show statistical significance with LTP?
When UC says:
It summarizes my layperson’s view of what LTP means with regards to AGW, trends and CIs.
Re: Kenneth Fritsch (#20),
In my experience, 100 to 200 points is about the smallest sample size where LTP typically starts to be visible and easily differentiated from white noise or serial correlation. The real problem is differentiating LTP from a deterministic trend or other phenomenon. That can be difficult even with very long samples.
Other researchers, including DrK and DrH above, have done more thorough studies than I have, but here (N=1500; N=15000) are some side-by-side graphics. Each column contains 10 simulations — realizations — of a FARIMA process. The first column of figures arise from a “white noise” stochastic process; the second column is AR(1) with rho=0.8; the third column is LTP with rho=0.8 and d=0.45 (which is about what you find in the instrumental temperature record). Note that the axes are not to scale — not even close — and were chosen to fit the range of the data. Also note that all of the underlying stochastic processes are stationary.
The graphs include a lowess smooth (red line) to emphasize lower-frequency signals.
The particular cases were chosen because they seem reasonable to me; you should try other cases that seem reasonable to you, however, so that you can develop a sense of how LTP works.
N=1500 was used because that is the length of the latest reconstruction/HS and I thought it might be interesting to consider which stochastic model might provide the best fit (FWIW). The case of N=15000 can be compared to the case of N=1500 to illustrate the scaling phenomenon.
If you look closely, you might be able to see hints of an ice age or two. 😉
Enjoy!
Re: TAC (#80),
Thanks much TAC for the plots and explanations. They tended to momentarily calm a mind and imagination all a twitter about this intriguing discussion.
http://www.climateaudit.org/?p=3486#comment-293627
Prof. Koutsoyianis, you say:
What, in you opinion, makes a model a “real climate model”?
I am of a different discipline ( high energy physics) and have been following this AGW story since last november, when I first started doubting the extreme statements coming from the IPCC. I have been reading up on all this since then and the more I read the more I am convinced that all these climate models are toy models, if by this you mean models that fit existing data but one does not expect them to be predictive.
Re: anna v (#21)
Anna, very good question – but difficult to answer. I am sure though that what I did in this paper is a toy model and not a real climate model. Perhaps you are right, the IPCC models are toy models as well – but complex toys. A real model should at least capture the important statistical properties of the climate. Perhaps a predictive capacity for climatic scales, e.g. for 100 years, is not feasible. But a model that could perform simulations that are faithful in the statistical sense may be useful. Such models could be stochastic or in any case be thought of as Monte Carlo simulation models.
I am really sorry for this off-topic comment but it is of crucial on-topic importance for this whole blog. Michael Mann (et al.) argues that the North is hottest in 1500 years, see
http://www.theaustralian.news.com.au/story/0,25197,24279210-11949,00.html
23 Motl
PennState Mann is still peddling his bristlecone fudge, apparently. What can one say?
Long term persistence and trends. Just as some effects like eddy formation can start on a very small scale, then grow into large storms, the concept of scale becomes so hard to pin down that one can’t really imagine a length for the “long” in LTP. That’s one reason I started on about spikes. Try the “Sea Ice Stretch Run” posts on CA about ‘baby ice’. If a high temperature spike melts ice, the next ice to form, the baby ice, appears to be easier to melt next summer as opposed to an accumulation of layers of ice over many years, that might form in the absence of a spike. So is the rate of melting of the ice an example of LTP, of a trend, or of an event caused by a spike?
How do you dissect them mathematically? Beats me. I favour looking at intervals between anomalous behaviour, like others have suggested elsewhere, looking at periods where a climate factor reaches a feedback of 1.0 then reverses, bouncing back time after time (but what time?).
Actually what your toy model does is to reproduce a non linear system with a positive Lyapunov coefficient (aka exponential divergence of orbits in the phase space of dimension 1) .
You can substitute to the tent function a very similar function :
X(t+1) = µ.X(t).[1 – X(t)]
It is also symmetrical wrt x = 0.5 , presents 2 fixed points , has a maximum for x = 0.5 and X takes values in [0,1] .
This is the well known logistic map .
The Jacobian is simply µ (1 – X(t)) so one can easily compute lim (n->oo) [|dX(n)/dX(0)|]^1/2n whose Log gives the Lyapunov coefficient .
It shows that the Lyapunov coefficient L becomes positive for µ values above roughly 3.5 even if there are still incursions to orbit convergence with L<0 above 3.5 .
It is exactly at that value where the orbits begin to diverge exponentially that the system enters the area of deterministic chaos .
There are no random components , no statistical laws apply and the prediction horizont varies like Log (dX(0)) / L .
By going only from µ 3.5 to 4 , L is multiplied by 10 and the prediction horizont reduced by 10 .
What your toy model is showing is that 1 dimensional deterministic chaos is enough to very accurately reproduce the variation of climatic variables (temperatures , precipitations) over VERY different time scales .
That is what I have been saying here for the past 2 years – climate is chaotic on all time scales from 1 hour to hundreds of thousand years .
It has infinitely amused me that Gavin Schmidt in a vain hope to save the predictive skill of “his” model has stated that it also reproduced chaotic behaviour and its Lyapunov coefficient was positive .
Because if it is true (and I believe it is) then the only difference between your toy model and “his” GCM is that you have a phase space dimension of 1 while he has many millions (tending to infinity when dx and dt tend to 0) .
Follows that the number of Eigenvalues of his Jacobian is also several millions as is the number of fixed points (or limit orbits in the Poincarre section) .
The stability analysis is then hopeless and he got himself a probably fractal attractor that doesn’t enable any prediction on ANY TIME SCALE .
In those cases what is called , improperly imho , LTP is the topological property of the attractor bassin that keeps the system on bounded but non periodic orbits .
Apparently the Mother Nature has chosen the values of the control parameters (like the µ in the logistic map) so that the system stays in the stability area forever .
Indeed the observation shows that over huge time scales of billions of years , the climate only unpredictibly fluctuates/bifurcates between very many apparently stable fixed orbits like hot Earth , ice earth , humid earth , stormy earth etc but the parameters never take values that would destroy the attractor and … us with it 🙂
Re: Tom Vonk (#26):
Thanks, Tom. I generally agree with what yo say. However, I do not think that the logistic equation exhibits LTP, despite that, indeed, well demonstrates unpredictability. That is why I used a slightly more complicated model in two, rather than one, dimensions. Please notice in eqn (20) that you need both u_t and alpha_t to define the system state (so, two dimensions).
re: #25
I think this statement should include a brief description of the conditions required in order for ‘very small scale’ to ‘grow into large storms’.
An ‘eddy’ in a flow field might grow into a very large storm only if a rather long list of specific requirements are met.
An arbitrary eddy in an arbitrary flow field is highly unlikely to meet the requirements for such growth.
Yes I have seen that .
I interpret your toy model as a discrete dynamical system defined by U(N+1) = F[U(N)] (no pun intended :)) .
As U(N) is a scalar , its phase space is dimension 1 both for the logistic map and for your model .
The introduction of alpha is for me equivalent to the introduction of µ (the logistic map with µ = 1 is not chaotic) and I interpret it as a control parameter like µ what doesn’t change the dimension of the phase space .
After all the logistic map is nothing else than the generalised tent with one advantage – it is differentiable everywhere over [0,1] .
Unfortunately I am not doing full time research in this field , it is more a hobby for me , so I have not the time to make the calculations and computer runs but I am convinced that you would get the same results by using the logistic map with a correct tuning of µ .
.
Just one more word about what I think about what is called LTP .
Clearly chaotic systems like your toy model or the logistic map have little memory and in the case of the logistic map it has been proven that the structure of the orbits is independent of the initial conditions when the system is in the chaotic area .
So what is it that “persists” ?
It is the topology of the phase space .
.
Even if most people scorn analogies , I will use one .
I am standing at the top of a slope with skis , the top is running horizontally N-S , E and W are deep valleys and I look to the North .
I get a slight push from the S and begin to slide slowly to NNW on the W side of the top .
Clearly my trajectory is selfcorrelated but the small push that sent me moving to the W valley attractor is forgotten .
Somebody making a statistical analysis of my movement would explain it in terms of a long term persistence of something .
Yet the only thing that controls now the trajectory is the topology of the slope , gravity and the many nonlinearities connected with the friction .
Now while I picked up speed (and there seems to be an obvious “trend” for the observer) I meet a small bump that deviates my trajectory to the right (East) and I cross the top beginning to descend to the opposite East valley attractor .
This is typically what happens in chaotic systems – small bumps that send trajectories in very different areas .
Yet there is no “long term persistence” of the causes (bumps) that changed the trajectories .
What one detects in the study of trajectories is not so much the dynamical variables and their variations but mostly the topology of the attractors .
As the attractors are the only TRUE invariants of a chaotic system it is they who persist when the system has forgotten everything else about its long term past .
Re: Tom Vonk (#29),
I do not think so. Let me put in another way. To describe the initial condition of the system we need two numbers, u_0 and α_0. If we change just one of them, then we get another trajectory. So you have two degrees of freedom.
If α were constant, this would be true. But α changes in time, following the same transformation. The difference is that the parameter changes.
Your analogy is interesting and I have to think about it.
Ian in #536:
Thanks for that, for I have a couple of distractions in mind. Maybe they can sometimes be helpful to lighten the load for us slower readers when the main interaction sparkles so much, such as between anna v and Demetris yesterday, or the challenges of the Vonk/Koutsoyiannis debate.
I’ve been pondering Demetris’ questions about, and difficulties with, English verbs last week. There are some things I didn’t say before, even in two bites of the cherry. Here’s a fuller response, which I would be happy to take to email from here on in, if that would be of any interest to a brilliant scientist whose message is of great importance to all readers of English.
Here are four useful words with similar meaning that generally take a human subject:
advocate
endorse
recommend
commend
For me advocate is the strongest of the four, the most ‘categorical’ as you put it. That is obviously not the case in the Greek. Thus you were misled by the Greek usage (not ‘drifted’, sorry, I didn’t have the heart to correct that one as well, but it’s a worse mistake than the other one, in all honesty.)
So, I was probably commending Tom’s thoughts to you but I wouldn’t have gone so far as to say that I recommended them – my immediate understanding wouldn’t stretch to that! I certainly couldn’t say that I advocated or endorsed them.
You can, by the way, commend a person, or recommend them, or indeed endorse them (which is often used in a political context, for example, ‘I endorse Barack Obama as the Democratic presidential candidate’ is stronger than the alternatives and, coming from the right person, would have had considerable punch a few months back, when the outcome was uncertain.) But, generally, one doesn’t use advocate like this.
Useful verbs or verb phrases for a abstract subject – like ‘falsification of GCMs’ – include (again, in decreasing order of strength, in my view):
imply
indicate
lend support to
suggest
tend to suggest
The tends to can be used to modify any of the three basic verbs. Support wouldn’t work on its own but ‘supports the thesis of’ might. This is clearly a very important area – a semantic minefield even – for you. The lists are by no means exhaustive, but I hope that in the blog situation especially they may come in handy.
For further help on written English, with which we all struggle, I would recommend (not advocate, which would be too strong 😉 ) Bill Bryson’s excellent works, including Troublesome Words and Mother Tongue. He has some interesting stuff on imply and infer in the former, for example.
Re: timeteem (#30):
Thanks once again for the correction and recommendations. I appreciate your attentiveness in English. I know the importance of word choice. It is equally important for Greek. In fact, I try to be as attentive as you – but in Greek. I also have posted some instructions about the correct use of the Greek language for my students (http://www.itia.ntua.gr/dk-el/hydroglossica/grammatica).
Unfortunately, I cannot be equally attentive in English due to my limited knowledge (I am mostly an autodidact, if this Greek word has some meaning in English, or self-taught, from the scientific books and papers I have read). My difficulties are even greater in blogs, due to the idioms used. I hope my terrible errors, like in ‘drifted’, do not offend your (and other folks) eye or your aesthetics.
Re: timeteem (#30)
Are you sure that you used the right words here? If yes, it must be my mistake to give the impression of debating with Tom (if I do not misunderstand the word ‘debate’). It would be very unkind of me (worse than mistaken word choice), given that Tom was discussing my own paper and offering me the opportunity to clarify what I have done (with respect to generalized vs. standard entropy).
Demetris (#33), I remain happy with my word choice. Debate has a hugely positive connotation to me – and I think to most people here. Nothing in what I said was meant to imply dissention (a word which is definitely negative) or lack of respect on either side. I commend you both!
Demetris (#32), without wishing to gush too much, you are remarkable and delightful. Given the brilliance of your thinking, your errors, which are mostly small, are simply endearing. It was ironic that the worst problem I noticed was in trying to respond to a correction of an earlier one. Or perhaps not so ironic, perhaps indicative of something like HK even within human psychology and language? (I’m not proposing a statistical test, at least for now!) Even then, all of us ‘got your drift’, an idiom that means we understood what you meant. And that’s a little bit of word-play from me, something that I admit I enjoy but that must make me extremely annoying for others to read at times. On my side, though, there is no offence at all. You invariably make yourself understood very well. (And autodidact is very good English, though self-taught is more common.)
One further socio-linguistic aside. My best friend in software engineering is far more proficient, and witty, in English than me. His comment during a discussion at work “I’m not a pedant in the strict sense of the term” is one of the funniest things I’ve ever heard in my own language – and probably not too hard to appreciate even coming from another mother tongue. But, despite his family deriving from Eastern European Jewish stock, Nick is very English and, dare I say, shares some of our prejudices against Americans. This was proved to me when I mentioned to him that I was enjoying one of the Bill Bryson books on the language just recommended. There was a definite sense of disdain or at least scepticism. A day or so later I told Nick a couple of things I had learned in the book, without revealing the source. He was fascinated, admitting that he found them both enlightening and delightful. It was a pleasure then to let him know that I’d learned both from Bryson.
This story won’t explain all the cross-cultural difficulties even we English-speakers can have on a blog like this but it may give you an indication!
timeteem #30
While I advocate, no while I endorse, no make that while I recommend, on further thought that should be while I commend your efforts to fine tune the descriptive language used in this discussion, I would think that Dr K’s responses have implied, or perhaps indicated or maybe merely lent support, or have, at least, suggested and certainly at a minimum tended to suggest a gentle put down.
Shouldn’t that be I?
Ken and Barney (#36 & 37) one part of what the professor said was all greek to me (which was very funny, and thoroughly deserved). I also misspelt dissension.
But I’d like to tell a last story, which is about more than language and is told with full permission of the friend concerned.
The day I last interacted with Ken here, exactly a week ago, I had to leave Climate Audit and other things because I’d arranged to meet a friend I’d not seen for a while, for a drink after work. Very sadly, a few minutes before she emerged, Olga learned on the telephone that her best friend in the world, in her early forties, had reacted badly to a serious operation for cancer in Kiev and was not expected to regain consciousness. (This in fact proved so, and we heard that she had died last Friday night, London time.)
Of course plans were immediately changed when I learned the news, the shock of which was made much worse by earlier lack of candour from the Ukraine about the seriousness of the condition, plus medical cock-up or at the very least lack of concern. Without hesitation I offered to drive Olga, who is from Russia, to see her daughter some miles away, who had also known Oksana and her family very well. This was around a two hour journey. At the start of it I asked a number of questions about the situation and Oksana herself. Not surprisingly, after a while I was told that answering such questions was too much for my passenger. But silence was also not a help. Could I please talk about something else?
There had also been anger and grief expressed about the current situation in the Ukraine and Russia and how it had made the suffering of Oksana, her mother and three children much worse. (None of the politics of which I tried to argue with, needless to say, even if I might have been inclined to in a less dire predicament.)
So, what to talk about? Well, I tried to describe the amazing things I’d been learning and the significance to the world of this thread on this blog. How does one communicate such things to a proud Russian whose English is not perfect and is trying to cope with such an enormity? And then of course the key fact came to me: Kolgomorov started it all, in 1940, even before Hurst. (Though writing in German, strangely enough.) This was a tremendous gift to us both.
I knew the tactic was working a little when we got on to how impolite some great scientists could be (I won’t say who I was thinking of here), I gave Sir Isaac Newton as an example and Olga wondered if the apple hitting his head might have been a partial explanantion.
But the point about Kolgomorov was very striking. I already liked Dr K and felt that I had gained much from him. But just this simple effort of honouring the ultimate pioneer of HK pragmaticity in his work had a spin-off benefit neither he nor I could have predicted one week ago. For which I will always be extremely grateful.
Tom,
In LTP stochastic process memory is needed, because the process is
not Markovian; in half-integration (#13), for example, all previous
states are needed to compute the present state.
Re # 28 Dan Hughes,
My poor wording – apologies. Others write about Amazon butterflies, not me. What I really meant was that a small eddy might occasionally grow into a large eddy-storm. The scales might cover orders of magnitude.
I’m still having trouble with LTP because I have not read enough specialism. I suspect I have seen cases where what might? be “LTP” have “jumped” up or down after a “spike” then shown a different “trend”. The answer I seek is whether this happens in Nature and whether maths can be devised or have been devised to cope with it, approximately or at all.
UC
Yes and it is the problem between physicists and statisticians .
To show LTP , it must be non Markovian – as I am not a professional statistician I don’t see any difference between both .
Now in physics we have generally a local law of nature expressed by some system of continuous PED/ODE .
The evolution depends only on initial and boundary conditions and those given , both the future and the past (by changing t in -t) are fully determined .
It is not a stochastic process so the notions of Markovian and non Markovian or LTP for that matter , make no sense .
.
Then there are 2 + 1 exceptions .
– the deterministic chaos . It is still a subcase of the general case in that the evolution is fully deterministic and depends only on the initial and boundary conditions . However here is the problem of predictability – due to the fast divergence of trajectories , the trajectories albeit unique and well defined are not computable beyond a certain time T (predictability horizont) . Yet as there is still structure and invariants in the phase space (attractors) , the topology can be used to extend the predictability .
Even if that looks a bit like statistics , the process is still not stochastic , there are no random variables and again the notions Markovian/non Markovian make no sense .
.
– the statistical thermodynamics . Here too there are local laws on the molecular level that would in principle be enough to determine the behaviour of the system . However , like above , there is again a computability problem but for another reason .
The computability was limited by the fast divergence in the chaotic case and it is limited by the huge number of molecules in the thermodynamic case .
Luckily isotropy and energy equipartition assumptions can be made and isotropy and energy equipartition ARE statistical statements (all X have an equal probability) . From these statistical statements can be derived all macroscopical statements (laws of thermodynamics) that are by nature statistical and it is not surprising that entropy appears in this way .
So as long as one takes a large number of molecules , their evolution could be considered as a stochastic process and I guess that the question whether this process is Markovian or not Markovian would make sense .
.
The + 1 exception is even more special in my eyes and this is what occupies us here .
The time series .
It is special because the underlying physical process that we observe must necessarily belong to one of the 3 categories above .
The question is which one .
My point , to make it short , is that any statistics make only sense if we are in the “thermodynamical” case what in my opinion is not the case of climatic variables .
If we exlude the deterministic computable case , the only physical alternative to the “thermodynamics” is the deterministic chaos .
That is why I appreciate so much D.K approach because he doesn’t postulate that climatic variables can be treated with standard statistics (AR1 , residues to LS etc) but looks at other methods .
Of course , he is still doing statistics on time series (what else could one do with a time serie ?) but the idea to apply statistics on a chaotic toy model which is by definition not a stochastic process could give some more insight on what seems to work and what doesn’t .
Re: Tom Vonk (#41),
Don’t give up so easily 😉
We have differential equations (laws of physics) and the system is subject to random forcing (hence statistical tools are needed). Just add them together, for example
(spring-damper with random acceleration input). As distance in time from the present grows, the random forcing term will take over. This system behaves nicely, but in the 1/f case we would need more state variables, say average of 10, 100, 1000, … previous output values, and the future value would depend on those values with approximately equal influence. With clouds, sun, oceans and lots of ice affecting Earth temperature, seems like a plausible idea.
—
Keshner’s ‘1/f Noise’ (Proc. of IEEE, Vol. 70, No. 3 1982) tries to address question What kind of memory is required for 1 /f noise?, and IMO the discussion section is very interesting.
Re: UC (#45):
In my opinion it is a wrong question and even the term ‘memory’ is a misleading term or a misnomer. There is no memory. Rather it is amnesia (see p. 582 in my paper The Hurst phenomenon and fractional Gaussian noise made easy; http://www.itia.ntua.gr/en/docinfo/511). The literal term is ‘dependence’ but even this does not help in understanding. In my opinion, dependence is the effect, not the cause of the Hurst-Kolmogorov behaviour.
A more understandable cause is the fact that there is nothing to ensure a stable local average. If we are somewhere in Himalaya, our local average (of elevation) is high; if we are in the Netherlands our local average is low. Do Himalaya have any ‘memory relationship’ with the Netherlands? I think, no. But if we take them both together (and all the places in between) we will have a Hurst-Kolmogorov type of image. This will be reflected in high autocorrelations, but it is the spectacular difference of local averages that caused this behaviour, including the high autocorrelations.
Now a hypothetical inhabitant of the Netherlands, who is ignorant of the existence of Himalaya, would hardly predict this existence based on his local conditions. That is why I think that the Hurst-Kolmogorov pragmaticity is closely related to unpredictability, uncertainty, and eventually maximum entropy (see also my comment in http://www.climateaudit.org/?p=3361#comment-291778).
Re: Demetris Koutsoyiannis (#46), A signal that traveses a communications line is “forgotten” the moment it is transmitted. There is no actual “memory” in the medium. But the medium can behave as though it had memory by modulating the speed of wave travel. “Memory” is thus an analogy. We all forget. But some forget sooner than others. Network flows through forgetful media are thermodynamic informational flows subject to HK pragmacity and LTP scaling behavior. 1/f noise is simply the statistical view of the physical-informational thermodynamic dissipation process.
This note is intended only to package the discussion for interested lurkers. Any corrections by DrK or UC are welcome.
Re: Demetris Koutsoyiannis (#46),
Re: bender (#48),
It seems that amnesia on the long-term is OK with me, where the process does not remember previous levels (and has no idea about next ones). But what makes the process stay close in the short term? The hypothetical inhabitant of the netherlands knows or “remembers” his surroundings, but if he goes far enough beyond his territory he may go up a mountain or fall into a canyon, he simply does not know where he is going. How can you describe this? It seems to me there should be some type of short memory combined with this long-term amnesia of the level. I think if it were total amnesia, we would get a white noise.
Re: K. Hamed (#52),
In what system? Climate? All systems? How about: unperturbed local entropy maximization (i.e. heat dissipation)?
Re: bender (#55),
I meant the climate system. I need to re-read Dr. K’s Paper on entropy.
Re: K. Hamed (#58),
I figured as much. That’s why I followed immediately with this (#56).
Re: K. Hamed (#52):
I think this is easy to understand. If its not raining just now, perhaps there are no clouds at all, so it is very probable that the next couple of minutes will be dry too. If the temperature is 25 degrees right now, I could bet that it would be around 25 degrees in the next couple of minutes. A rapid change would need huge amounts of power/energy, which is not available. The ‘white noise’ in continuous time, which implies an arbitrary large change in arbitrary small time is just a mathematical structure.
Re: Demetris Koutsoyiannis (#46),
I have to disagree with this, Keshner’s reasoning for the question is
..and to generate 1/f you indeed need memory, which is clear when one tries to make a computer program that generates such process.
But in this point we need to remember that your articles mostly discuss stationary processes, and exact 1/f is not stationary. That caused some confusion earlier in this thread.
Mark T.,
Hmmm, if you can model it as infinite series of resistor-capacitor sections separated and isolated by unity-gain buffer amplifiers 😉 , where each section can remember one number.
Demetris #62,
Why then ‘ 1/f noise ‘ wouldn’t be a mathematical concept? I agree that term ‘noise’ causes much confusion in natural processes, often climatologists remove noise without properly defining signal and noise. Usually mathematical formulation helps to avoid confusion.
Re: UC (#81):
Thanks for expressing your disagreement, which offers me the opportunity to clarify how I understand a few more things related to this discussion.
Perhaps you were misled by the term ‘1/f noise’ and thought that ‘1/f’ is nonstationary. In the first few lines (first equation) of his paper, Keshner defines the ‘1/f’ process as that whose spectrum is proportional to 1/f^γ, where γ is between 0 and 2 (isn’t it a bad name, if by 1/f we mean 1/f^γ, — let alone the fact that f is a symbol rather than an English word). In particular: (a) for γ less than 1 the process is strictly stationary, whereas (b) for γ greater than 1 the process is indeed nonstationary – in fact it is a cumulative process that is derived by aggregation of a process of the category (a). For instance, using Mandelbrot’s terminology, the fractional Brownian noise is a process of category (b) and it is the cumulative process of fractional Gaussian noise, which is stationary and belongs to category (a).
Furthermore, even the processes of the category (b) in this theory (Keshner, Wornell) are stationarized, by bounding the frequency above and below (e.g. p. 215 of Keshner and more explicitly in Wornell, Wavelet-based representations for the 1/f family of fractal processes, Proceedings of the IEEE, 81(10), 1428-1450, 1993, p. 1435, Theorem 1). Thus, in effect this theory deals only with stationary (or stationarized) processes.
Both the above papers have been published in the Proceedings of the IEEE (Institute of Electrical and Electronics Engineers), where the term ‘memory’ has a meaning (also, the terms, ‘signal’, ‘noise’, etc.). But, in my opinion, using such terms in natural processes, e.g. in climate, even as metaphors, may create strong difficulties in understanding and even in modelling.
It is easily understood that mathematically constructed (i.e. abstract) cumulative processes, are nonstationary. For instance the random walk process, which is the cumulative of the white noise, is nonstationary: Its variance is proportional to time t (variance = k t, i.e. a deterministic function, obtained by deduction, i.e. mathematical proof). However, a natural process is different; there are some physical boundaries that make natural cumulative processes stationary (e.g. the Brownian motion in a glass of water is stationary) or some loss in the accumulation (e.g. the evaporation loss in a lake fed by a river) or both. Even a slight loss, e.g. proportional to storage, results in a strictly stationary cumulative process. These things I have discussed in a presentation in EGU 2008 (http://www.itia.ntua.gr/en/docinfo/847).
A last point. You say ‘to generate 1/f you indeed need memory, which is clear when one tries to make a computer program that generates such process’. I agree with this but what is mathematically convenient may not necessarily help in understanding. For instance, to calculate the probability of exceedence of a normally distributed value x, we numerically integrate its pdf from x to infinity. This does not help understanding the normal distribution and the reasons of its widespread presence.
Re: Demetris Koutsoyiannis (#83),
I couldn’t agree more. That’s why I said the memory concept was an explanatory device. Like all explanatory devices and analogies, they are training wheels – not vehicles – for understanding.
1/f^y 🙂
Re: bender (#88):
I take this as a signal that I overdid it. After all, understanding is a subjective process. So, if ‘memory’ helps you in understanding, this is fine with me. But perhaps you must be prepared that people who dislike/fight Hurst-Kolmogorov may say (they have often said to me also, even though I am not the one promoting the ‘memory’ interpretation) that ‘memory’ is fine (read: Markovian processes are physically reasonable) but ‘infinite memory’ is nonsense (read: Hurst-Kolmogorov processes do not have any physical meaning).
Re: Demetris Koutsoyiannis (#91),
Thank you for explaining your criticism. It’s a shame what one must do these days in order to pre-empt spurious argumentation.
I have learned much from your papers, and also from this discussion with UC, Tom Vonk, TAC, and others. Anyone who thinks I come to a discussion unprepared to listen and learn has now been proven wrong.
Re: Demetris Koutsoyiannis (#91),
In an attempt to apply the concept of LTP resulting from randomness at all time scales, I did the following experiment, which 5 minutes later I found out to be a simplified version of Dr.K’s “multiple time scale fluctuation method” in his paper [Koutsoyiannis, D., (2002). The Hurst phenomenon and fractional Gaussian noise made easy. Hydrol. Sci. J., 47(4), 573-595.]. Nevertheless, I thought I’d share the results with you as I think it might help us understand the “amnesia” or “no memory” concept.
If we imagine that a time series is the summation of a number of components at different scales (i.e., 1 yr, 2yrs, 4 yrs, …) and that the variation at each scale is random (no memory). Then we may generate an approximation by actually generating random numbers at each scale and then add them up. I wrote the following MATLAB program for this purpose
clear;
maxl=10; %number of scales (How high can you go?)
repl=10; %number of repetitions of the highest scale
totn=k(1)*repl; %total number of 1yr points in series
k=2.^(maxl:-1:0); %number of 1yr points at each scale
x=zeros(totn,1);%allocate memory for the 1yr series
for i=maxl:-1:0 %cycle through sacles
a0=randn(1,repl*k(i+1)); %generate random values for current scale
a1=repmat(a0,totn/k(i+1)/repl,1);%resample at 1yr intervals
a(:,i+1)=a1(:); %store individual resampled scales
x=x+a(:,i+1); %add to generate the combined series
end;
plot(x)
As I said before, this, I think, is a naiive application of the method (maybe too naiive, but I remember seeing some fast FGN generator using a similar idea, but my “memory” is not helping), but the resulting time series exhibit all the properties of LTP data: slow decaying FGN-like ACF, high H values, red-noise spectrum, … etc. I even got my own Hockey stick in many realizations.
It is clear that no memory of any kind has been used to generate this data (not even short term AR(1)). Also the process is stationary at all the scales that we generated (theoretically including the mean, which should be at scale infininty?? and cannot be measured accurately with limited data??)
In my openion, “apparent memory” was introduced at line 9 of my code when resampling the larger scales, where now the larger scales appear to persist at a certain value for some time equal to that scale (constant in this implementation, but these periods can also be random). So with real data LTP may be the side effect of sampling the series at 1 yr scale but looking at the effect from all scales at the same time.
I don’t know how much this relates to Dr.K’s vision, but I await your comments. I do not believe any of this conflicts with the maximum entropy prenciple, does it?
Re: K. Hamed (#93),
Careful. That the generating “process is stationary” is in this case known by a priori insight, not by logical deduction. In the case of a short sample realization where you don’t have such a priori insight, the inference would have to be that the sample data are indicative of a non-stationary generating process. Or, to satisfy Vonk’s observation, the product of an invariant complex topology.
For earth’s climate system, this is a question. There are insights from thermodynamic theory and there are statistically interpreted observational data. But the true nature of the pattern generating process (externally forced N-S) can not be presumed. Whether you conclude ‘statistical stationarity’ depends upon your presumptions about attractor topology and its time invariance. An incorrect presumption may lead to an incorrect inference.
At least that’s what I take away from this discussion. Stationarity is relative to your assumptions about topology.
Re: bender (#94),
I think it is not by insight but by construction. So it is fine.
Re: Demetris Koutsoyiannis (#96),
Construction is to insight as god is to man. We cannot know god; we can only play at construction.
There are data. And then there are data that underly the process that generated the data. If you can reconstruct time-invariant topology you can have the insight required to make a judgement on stationarity without appeal to statistical methods applied to short samples. In this case you can appeal to theory, which, once validated, is Law.
H-K behavior of N-S seems to be the key.
Re: bender (#98),
While I find your analogy interesting, it is the next sentence that really hit me:
While this theological truth is widely acknowledged, in practice it seems to be more honored in the breach than in the observance. FWIW, I’m with you, bender; but I also notice the multitude successfully promoting “play constructions” as representing God’s creation.
We live in interesting times.
Re: K. Hamed (#93),
I accedentally switched lines 4 and 5 during my final formatting. The correct code is
clear;
maxl=10; %number of scales (may be infinite?)
repl=10; %number of repetitions of highest scale
k=2.^(maxl:-1:0); %number of 1yr points in each scale
totn=k(1)*repl; %total number of 1yr points in series
x=zeros(totn,1);%allocate memory for the 1yr series
for i=maxl:-1:0 %cycle through sacles
a0=randn(1,repl*k(i+1)); %generate random values for current scale
a1=repmat(a0,totn/k(i+1)/repl,1);%resample at 1yr intervals
a(:,i+1)=a1(:); %store individual resampled scales
x=x+a(:,i+1); %add to generate the combined series
end;
plot(x)
Re: Demetris Koutsoyiannis (#83),
Thanks for your reply, little disagreement is sometimes good for the discussion.
Keshner’s paper starts with
and I mentioned exact 1/f,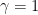 , Keshner:
, Keshner:
As the process is nonstationary, the problems in estimating Hurst coefficient arise, as discussed earlier.
I agree with ‘signal’ and ‘noise’, but I’d like to keep ‘memory’ 😉
Subjective issue.
..or use cumulative distribution function 😉
Re: UC (#102):
Thanks UC – indeed the disagreement is little as you say. I understand you do not disagree with my main point that in effect this theory deals only with stationary (or stationarized) processes. A couple of additional little disagreements:
I do not think so. The cumulative processes of this type has a well defined Hurst coefficient, which is precisely equal to the one of the stationary process, from which the cumulative process is derived. For example, the white noise has Hurst coefficient H = 0.5 (and γ = 0) and the random walk process has again H = 0.5 (and γ = 1, as you say). (Here I recognize that lots of publications have confused this — but one should better refer to Mandelbrot and van Ness, 1968).
The problem in estimating the Hurst coefficient is uncertainty, which increases with H (for H = 0.5 the uncertainty is not a problem).
OK, but the normal distribution function contains an integral (from -infinity to x) that is not calculated analytically.
Re: Demetris Koutsoyiannis (#103),
Random walk should be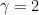 ? I think Mandelbrot is very right when saying that
? I think Mandelbrot is very right when saying that
The problem I’m referring here is the existence of of Eq 3 in your Hydrological Persistence and Hurst Phenomenon paper. If the process is non-stationary, this variance doesn’t exist. Earlier Spence wrote
of Eq 3 in your Hydrological Persistence and Hurst Phenomenon paper. If the process is non-stationary, this variance doesn’t exist. Earlier Spence wrote
http://www.climateaudit.org/?p=3361#comment-283642
(I think we have 3rd version of similar algorithm in here http://www.climateaudit.org/?p=3486#comment-294882 by K. Hamed , BTW )
4H-2 or 2H-1 , that’s still a bit unclear to me.. More math, less words, we’ll figure it out 😉
Re: UC (#121):
First, thanks for the correction; indeed random walk is γ = 2. These things must not be difficult to clarify. The problem must be, in my opinion, in the conflicting and confusing information in the literature. I will try to describe the essentials from scratch, as I understand them, and I am awaiting reactions to see if these can be agreeable. I will only use discrete, rather than continuous, time (sacrificing generality and perfect rigorousness).
Let us start with a sequence of independent identically distributed (iid) variables X_i, with i denoting time. We can call the sequence X_1, X_2, X_3… a stochastic process in discrete time. Because all X_i are identically distributed (distribution not dependent on time i) the process is stationary and, given its independence, we can think of it as ‘white noise’ (although this term literally refers to continuous time processes). Let us assume that in discrete time, the process X_i has a finite standard deviation σ. If we construct the power spectrum of this process, it will be a flat line (all frequencies have equal power), which justifies the term ‘white noise’.
Let X_1(k) denote the time average of k terms of the process, starting from term 1, i.e. X_1(k) := (1/k) (X_1 + X_2 +… + X_k). Given the independence, we can easily conclude (using typical algebra of independent variables) that the standard deviation of X_1(k) is StD[X_1(k)] = σ / k^(1/2). This is a fundamental equation in classical statistics, implying that the uncertainty of the estimate of the mean is inversely proportional to the square root of the length of the sample.
Now we construct the cumulative process: Y_1 = X_1, Y_2 = X_1 + X_2, Y_3 = X_1 + X_2 + X_3 etc., or in general Y_i = Y_[i-1] + X_i, with Y_0 = 0. An obvious consequence from the notation of the previous paragraph is Y_i = i X_1(i). The process Y_i is no longer a stationary process. For, using the above fundamental classical statistical result, we get: StD[Y_1] = σ, StD[Y_2] = 2^0.5 σ, StD[Y_3] = 3^0.5 σ, or more generally, StD[Y_i] = i^0.5 σ. That is, the standard deviation of the process Y_i is a deterministic function of the time i. For i tending to infinity, the standard deviation tends to infinity too. However, for finite time the standard deviation is finite, but different in each time. It is not correct, thus, to say that the nonstationary process has infinite standard deviation.
While the stationary process X_i has been called ‘white noise’, loosely, the cumulative nonstationary process Y_i can be described with several names such as ‘random walk’, ‘Wiener process’ and ‘Brownian motion’. Note though the last two terms literally refer to continuous time processes and the first term literally refers to the case where X_i takes the values +/-1. Because Y_i – Y_[i-1] = X_i, we say that the process Y_i has stationary and independent increments (X_i). However, obviously the process Y_i is neither stationary nor independent in time.
As Y_i is a nonstationary process with variance (and covariance function) that is a function of time, its power spectrum depends also on time and, due to its dependence, this spectrum is no longer flat. Based on the stationarization technique by Keshner and Wornell mentioned somewhere above, we can assign a stationarized spectrum for Y_i, even though Y_i is strictly nonstationary. In effect, this spectrum is calculated as if the process were stationary. It is shown that the power spectrum is inversely proportional to the square of the frequency f, i.e. proportional to 1/f^2.
Of course, the iid process X_i is a trivial and non-natural case. We seek to introduce some dependence to the consecutive X_i, in order to have a plausible representation of a natural process, yet keeping its stationary setting. An easy means (perhaps the easiest) to do this is to generalize the classical statistical result StD[X_1(k)] = σ/k^(1/2), so as to read StD[X_1(k)] = σ/k^(1-H), where we call H the Hurst coefficient. Apparently then, StD[Y_i] = i^H σ. The value of H should be between 0 and 1. The value H = 0.5 corresponds to the case of ‘white noise’ / ‘Brownian motion’. Notice that the same H = 0.5 corresponds to both processes, the stationary X_i (white noise) and the cumulative, nonstationary Y_i (Brownian motion). In this respect, I would not adopt Pilgram & Kaplan’s convention (in comment http://www.climateaudit.org/?p=3361#comment-283334) that H = 1/2 in white noise and H = 1 in Brownian motion.
Except for the new law for standard deviation (which implies dependence in time), the nonstationary cumulative process Y_i can be constructed from the processes X_i in the precisely the same manner as above. Now we call X_i a ‘Hurst-Kolmogorov process’ or a ‘fractional Gaussian process’ (provided that it is indeed Gaussian) and the process Y_i a ‘cumulative Hurst-Kolmogorov process’ or a ‘fractional Brownian motion’ or a ‘self similar process’. Because Y_i – Y_[i-1] = X_i again, we say that the process Y_i has stationary (and dependent) increments and we also call X_i ‘stationary increments of a self-similar process’.
In this case, it can be shown that the power spectrum of the (stationary) HK process X_i is inversely proportional to f^(2H-1); see derivation in Koutsoyiannis, D., The Hurst phenomenon and fractional Gaussian noise made easy, Hydrological Sciences Journal, 47 (4), 573–595, 2002; equation (19). On the other hand, the (stationarized) power spectrum of the cumulative HK process Y_i is inversely proportional to f^(2H+1). So if we wish to write the same expression for both associated processes X_i and Y_i, i.e. s(f) = a/ f^γ, then
γ = 2 H – 1 for the stationary HK process
γ = 2 H + 1 for the nonstationary cumulative HK process
Conclusions:
1. The same value of H characterizes two associated processes, a stationary HK process and a nonstationary cumulative HK process. The value of H should be between 0 and 1. The case H = 0.5 corresponds to the white noise and the Brownian motion. Any algorithm that estimates H > 1 must have some inconsistency.
2. Calculation of the power spectrum of the nonstationary cumulative HK process presupposes its stationarization.
3. There is not a single relationship between the Hurst coefficient H and the exponent γ of frequency f in the power spectrum. Rather, they are two different relationships for the two associated processes.
4. The stationary HK process need not have an infinite variance or standard deviation. Rather it allows assuming a finite standard deviation σ.
5. The nonstationary cumulative HK process need not have an infinite variance or standard deviation. Rather it may have a finite standard deviation, which is proportional to the square root of time.
6. As time tends to infinity (equivalently, if we do not know the initial ‘position’ Y_0 of the cumulative process) the standard deviation of the cumulative HK process tends to infinity and the process itself tends to be become stationary.
Re: Demetris Koutsoyiannis (#122),
Excellent, slowly catching up.
And the process X is stationary, and thus StD[X_1(k)] = StD[X_50(k)] = StD[X_1000(k)], etc. ? Furthermore, as X is stationary, process Y has stationary increments. But not necessarily independent increments, that would lead to random walk.
Now, if we apply some estimator of H to a nonstationary process, we get nothing useful as H is not defined then. Next question is, does 1/f ( ) process have stationary increments ?
) process have stationary increments ?
And related to this, where can I find a copy of Granger, C. W. J. & Joyeux, R. (1980). An introduction to long-memory time series models and fractional differencing. J. Time Series Analysis. 1, 15-29 ?
Re: UC (#128), Some replies to your interesting questions:
Exactly.
Yes, the self similar process Y has always stationary increments X. These will be independent only if H = 1/2 (Y random walk, X white noise).
Why? H is defined for the cumulative nonstationary process Y, as well, and it has same value as in the stationary process X. So, if we know that the process is cumulative (type Y), then we take the differences (X) in consecutive time intervals and apply the algorithm to the X time series which is stationary. Alternatively, the spectral method could be also applied for Y and H be estimated using γ = 2 H + 1. But the differencing method is much better as it does not involve any assumption and theoretical problem.
Good question. I am not well prepared to answer it. Mandelbrot and van Ness’s (1968) Proposition 3.7 says that a cumulative HK process Y with stationary intervals X will necessarily have H less than 1 (not ‘less than or equal to’). Generally, the case γ = 1 can be viewed as a limiting case. In can be either the upper limit of a stationary HK process X for H tending to 1 (indeed, γ = 2 * 1 – 1 = 1) or the lower limit of the nonstationary cumulative HK process Y for H = 0 (γ = 2 * 0 + 1 = 1). According to Beran’s (1994) book (p. 53) such cases are not of practical importance. However, Keshner, as you described, gives an example with practical importance. So, perhaps Keshner’s example of γ = 1 may not belong to the family of cumulative HK processes, which have stationary intervals. I have to work on this further.
http://www3.interscience.wiley.com/journal/119858439/abstract (I hope you do have access, otherwise send me and an email).
Re: Demetris Koutsoyiannis (#136),
I meant that if we put Y directly to H-estimator that assumes stationary process, confusion might arise. As has happened earlier in this thread; those Matlab estimators gave H close to 1 for random walk and H around 0.75 for 1/f.
Yes, I think this path is worth exploring. Stationarity assumption might lead to overconfident predictions 😉
Re: Demetris Koutsoyiannis (#136),
Demetris, thanks for the paper. From Table 1. I infer that 1/f is indeed a process with stationary increments (if half-integrated white noise is accepted as a definition for discrete-time 1/f ). V(d) exists for d=-.5 . It is also interesting that
i.e. this forecast beats the simple average easily, if the model is correct. Climate becomes forecastable 😉 My model has d=0.5, i.e. the series is non-stationary. With d=0.45 it wouldn’t be, but who could see the difference from a small sample ? I’d select non-stationary, Earth will be swallowed by the Sun, but it takes some time..
Re: UC (#81),
UC here clearly shares my view.
Re: UC (#45),
Damped , forced pendulums are known to have chaotic modes .
No need to have random forcing , a deterministic forcing does the job too .
In this case the system has no memory (LT or otherwise) .
What’s physically happening if the forcing is random ?
Well you get a chaotic mode too .
Has the system magically acquired a memory ?
I do not think so . I would conjecture that the chaotic attractor is identical in both cases .
But if so , then the shadowing lemma would allow me to substitute to any orbit created by the model with random forcing an identical orbit with deterministic forcing .
The system doesn’t care about “details” because it keeps forgetting them – that is already what I have written above – deterministic chaos is not random , what matters is the topology .
Autocorrelations that could (eventually) appear in a statistical study of a chaotic system should not be interpreted in terms of memory but in terms of scale interaction .
I am here with Demetris and the hypothesis of changing means .
I am not sure about the random part because there is nothing random in deterministic chaos but if the means behave also like the forcing in the example above , then one could conjecture that means changing deterministically but chaotically would be equivalent to means changing randomly (here equivalent means producing the same chaotic attractor who is a topological invariant of the dynamics of the system) .
Actually I must think more about that because I think that there could be indeed a way to prove that equivalence and perhaps there is even somebody out there who already looks at this .
Re: Tom Vonk (#84), I think it is helpful to distinguish between processes with a stationary mean and processes with a stationary topology – where that topology can not be described by a single parameter, such as a mean. Most statisticians, I think, are uncofortable with the idea of complex topology, and prefer to work with simpler topologies, such as single point attractors. This may help clarify yesterday’s narrow-mindedness on my part.
Re: bender (#86),
Of course !
It is not only helpful but necessary – those are 2 completely different things .
The right word is topological invariant and not stationary topology because we are not considering general relativistic corrections 🙂
Stationary mean is just a property over a certain time interval .
What I conjecture in the post above is that a system containing random subsystems and going in the chaotic mode is equivalent to the same system containing only deterministic subsystems .
Equivalent being defined as having the same topological invariant (e.g chaotic attractor) .
If that conjecture is right , then it means that there is no dependence on distant past in any time serie extracted from a chaotic system even if there were long selfcorrelations that would appear in a statistical analysis of that serie .
That’s why the argument that to construct chaos from randomness it is necessary to fix long past parameters would be irrelevant because the answer is “Don’t construct it from randomness then .”
Insofar I consider also the term LTP misleading .
Geoff Sherrington
The math part is easy – yes there is an extensive corpus of litterature that deals with the ergodic theory , non markovian processes and LTP .
To be fair , it doesn’t really belong to the easiest part of mathematics .
I have read recently a paper showing that most (all?) non markovian processes can be transformed in markovian processes – a non statistician struggles hard with such a paper .
Especially that if I understood well that paper , it would mean to me that LTP doesn’t really exist but is an artifact that can be eliminated by a transformation .
Now it may well be that I misunderstood .
As for the physic (Nature) part , I think that LTP is badly defined . It is a statistical concept that doesn’t translate easily in physics .
I said more to this part in the post above .
A point-wise climatological time-series is a curious thing. It is a very small slice of a much larger structure. If you study many such slices independently I am not certain one gets to understand the whole. In my sophomoric view, LTP is the point-wise time-series manifestation of a much larger-scale thermodynamic process as it plays out. We arbitraily decide that what occurs at the time-series sampling point is “internal”, and that what occurs in the great beyond is an “external” perturbation to that which is internal. But what justifies this choice of “internal” and “external”? It is merely by convention, or tradition: that is how the data are collected. LTP is a way of understanding large, long excursions in a series that are imposed by outside forces. If just happens that those external forces, in this case, are the very same as the internal forces, just at a larger scale.
Global-scale LTP would be a very different thing. Something I’m not prepared to comment on.
That it’s idiomatic English is what makes it difficult.
Is this a better question:
How is it that all kinds of thermodynamic ‘amnesia’ lead to 1/f noise?
Re: bender (#48),
My simple understanding of this is that it is related to an attractor in a chaotic system. It seems to me that General Systems Theory shows that sufficiently complex systems tend to show similar patterns of behavior regardless of the underlying mechanics.
Is this understanding off in some way – are you suggesting that there must be other mechanisms causing this (other than general systemic interactions) or are you wondering about the specifics of how these attractors come about in this particular domain?
Re: Richard Patton (#54),
No, I don’t think so, although there’s lots more to it. But I will let UC and DrK take this matter up. I am basically brokering a converstaion – which I really have no right to do without asking first. Who knows – I may even get hoovered.
Re: bender (#48):
I insist that ‘memory’ is not a good analogy for understanding. ‘Amnesia’ would help a little more but I think the analogy I gave with the Netherlands and Himalaya is even better. I will try to combine them.
Take a cross section of the relief from the Netherlands to Himalaya (not necessary to do this – just imagine; I have not done it either). You will see a relief with several patterns, totally different from ‘white noise’. Calculate lagged correlations and you will see that they are very high, even for large lags. Imagine that you substitute time for distance in the horizontal axis keeping the shape as is. You have a time series with high autocorrelations. They are high because of the patterns with different local averages and not because of any type of ‘memory’. This is a natural analogy.
Now simplify this with a much easier example, more mathematical than physical, but trying to mimic in an easier manner the earlier natural analogy (please do this easy thing – do not rely only on imagination). Make a column in a spreadsheet with 1000 uniform random numbers (‘white noise’), assigning time steps 1 to 1000 to each number. Calculate the mean, which will be around 0.5, and the autocorrelations for lags, say, 1-100, which will be around 0 for any lag. Now assume that your process, at time 500 forgot that it should have mean 0.5 and implements a mean 1.5. So in another column, add 1 to each of the last 500 numbers (so as to have mean 1.5) and leave the first 500 unchanged (mean 0.5). Calculate again the autocorrelations and plot them. You will see that they are high, even for high lags (for instance, at lag 100 you will have autocorrelation of about 0.60). Is that a result of memory or of amnesia?
This simple example will not generate precisely a Hurst-Kolmogorov process. But if you take more ‘amnesia’ steps, at different time scales (e.g. 50, 500, 5000, etc., you will get a good approximation of an HK process. Also the changes in the mean (the ‘amnesia’ steps) should not be regular but irregular, as better described in the paper I mentioned above.
I have agreed with Timeteem about the importance of word choice. May I mention also the — even higher in my opinion — importance of the choice of scientific terms. Personally, I try to avoid terms such as ‘memory’, ‘1/f’ and ‘noise’ when referring to natural processes (except in ‘white noise’, which by definition is a mathematical concept).
Re: Demetris Koutsoyiannis (#62),
From a signal transduction perspective, the memory was encoded by the geological processes that created the relief in the first place. And for every memory-free pattern there is always a memory-laden generating process.
Re: bender (#64):
Please refer to the relief example as a simple topographical analogy and not try to explain how the mountains were created.
Re: Demetris Koutsoyiannis (#67),
You deny the concept of memory by asking me to not consider the process that generated the pattern? This is circular reasoning. EM is a TD process. It makes sense to look at the processes if the goal is to interpret observed patterns.
But I will step back and let you resolve your differences with UC.
Re: Demetris Koutsoyiannis (#62),
Yes, the switch was a result of amnesia: a willingess to switch to a new value under some demonic intrunsion from outside. It is the tendency to stick around one value or another for a long period of time that indicates “memory”. The calculated ACF is uninformative, or rather, misleading – being the product of a non-stationary process for which there is no one defined theoretical ACF.
Re: bender (#65):
The process is not non-stationary. The process is stationary. Please notice my clarification: ‘Also the changes in the mean (the ‘amnesia’ steps) should not be regular but irregular, as better described in the paper I mentioned above‘ and please refer to the paper where I show mathematically that the process is stationary.
Re: Demetris Koutsoyiannis (#68)
DrK, I was referring to your spreadsheet example in #62. You specified a mean of 0.5 and then specified a mean of 1.5. That is by definition a non-stationary process. Processes like that – where the mean switches from one expectation to another – are, by definition, first-order non-stationary.
Re: bender (#69):
Bender, sorry but I think this is not correct. If the switching is done according to a deterministic law, then indeed the process is nonstationary. If the changes are done in a random manner, then the process is stationary. A change does not necessarily imply nonstationarity. Only a deterministic change implies nonstationarity. So in my example, the time 500 in which the change happened was not given by any deterministic law; perhaps I produced it by a random generator. (I can now repeat my random experiment which may give a change in time 300).
More about stationarity and nonstationarity in my paper ‘Nonstationarity versus scaling in hydrology’, http://www.itia.ntua.gr/en/docinfo/673 — with my apology for repeatedly citing my own papers.
Re: Demetris Koutsoyiannis (#73),
I agree with the first statement. The latter statement I may agree with if you could first explain to me which forcing agents in the physical world are “random” and why you choose to demarcate between deterministic nonlinear chaotic processes (which all random number generators are) vs. truly random processes, which are functionally indistiguishable.
Is entropy maximization under N-S not a fully deterministic problem? And so, is the point-wise time-series output of a N-S climate model not non-stationary, according to your own definition?
My apologies. You are confusing me with what seem to be many internal inconsistencies.
Re: bender (#74):
Bender, your first question is rather philosophical. I would say that random is non-deterministic. According to Karl Popper (Quantum Theory and the Schism in Physics, ed. by W. W. Bartley, Unwin Hyman, 1982) determinism is related to predictability. Predictability is meant a priori, for a phenomenon that will occur in the future (not something that is verified a posteriori based on observations).
About the second question, my reply cannot be summarized in a few words but I think it is contained in the paper ‘Nonstationarity versus scaling in hydrology’ mentioned above.
I must leave now – it’s midnight. We can continue the fascinating discussion tomorrow.
“Long-term” “amnesia”?
Sorry bender, but this isn’t exactly true. Nearly any practical communication system has definite memory, not apparent memory. Memory in a communication system is due to multipath (though you can also consider the time it takes to travel from point A to point B memory, too, with duration that is a function of the speed of travel as you correctly mention). Multipath results in a time spread of arriving signals, which is often modeled as a tapped delay line, and each of the taps (channel weights) is separated by a memory element (which are spaced at 1/W s, where W is the channel bandwidth, in Hz). Filtering also induces memory by spreading the energy of a bit/symbol over time. Of course, this memory is on the order of microseconds (at least very small) due to the fact that it is a result of speed of light phenomena.
Now, how this relates to the discussion at hand, I’m not sure. I.e., is there an analogy between multipath/channel delay in a communication system to these thermodynamic flows? I can’t say, so your analogy remark may actually be closer to the truth of what is occurring.
Mark
Re: Mark T. (#50),
Fair enough. All analogies break down when you push them too far, as one is wont to do.
Are there communications network media that exhibit “ready willingness to episodically forget old memories and take on new states”? Sounds like a computer crash to me. I wonder how faithfully computing network failures follow a 1/f distribution: lots of little crashes, a few biggies, all in keeping with the principle of maximum entropy (dissipation of information through episodic amnesia).
If I may personify the thing – It’s a system’s suprising willingness to let go of old memories that allows it to so easily take on new identities.
IOW states that we thought were “persistent” may turn out to be transient. And so the system bounces from one transient substate to the next, the transient substates “persisting” for relatively long periods – relative to the short time it takes to forget such substates. Selective amnesia.
Some may find a Lorenz butterfly attractor to provide a helpful analogy. Others who’ve lost themselves during a week in Vegas might relate.
Global-scale entropy maximization (heat & information dissipation) occurs through a hierarchical cascade of increasingly local entropy maximization (EM) processes. A change in local state may indicate a conflict between a local entropy maximization process as it is being forced by a larger scale entropy maximization process. In the face of such forcing a local sub-system may be willing to forget what it WAS doing (past states), and proceed with a new EM agenda (i.e. different state) as initiated by the hierarchy and pursued by the local EM process.
#56 is speculation on thermodynamics – something that Steve M has actively discouraged in the past. I offer these comments only in an attempt to understand how UC and DrK may be debating at cross purposes over the semantics of “memory” vs. “amnesia”. I would not encourage others to follow where I have trod. It is very weedy out here in the weeds.
To satify Mark T’s #50, I should amend #47:
as:
I’ll buy that a bit more, bender. I’d tend to call system delay “apparent memory,” whereas the comm problem of multipath is actual memory (it’s actually a FIFO, if you think about it).
When you say:
you may be correct. Two different viewpoints of the same phenomena. Pat Keating and I did the same thing once regarding discontinuities in discrete Fourier transforms (technically we were discussing the FFT).
Mark
I too do not like the 1/f noise model when there are more informative ways of interpreting autocorrelation patterns as the product of a memorized/forgotten signals. However for statisticans who deal in i.i.d. models it is a useful alternative null model that allows us to cope with memorized signals whose mechanistic causes are unknown to us. It may be an internal signal of unknown origin, but that doesn’t mean it can’t be treated as though it were an exogenous noise. Sometimes one model will be more applicable than the other.
The context that matters here is that the forcing attribution exercise conducted by IPCC scientists relies on an overfit i.i.d. statistical model. You have two choices here. Re-invent the model completely. Or simply ask them to examine the consequences of assuming a different error structure, such as 1/f. The latter is not invalid.
In fact they are also second-order non-stationary, with respect to the second-order moment of inertia = variance.
A very scholarly and interesting paper has popped up on physics.ao-ph
http://arxiv.org/abs/0809.0632
How to cope with climate’s complexity
Authors: Michel Crucifix
(Submitted on 3 Sep 2008)
Abstract: Climate exhibits a vast range of dissipative structures. Some have characteristic times of a few days; others evolve on thousands of years. All these structures are interdependent; in other words, they communicate. It is often considered that the only way to cope with climate complexity is to integrate the equations of atmospheric and oceanic motion with the finer possible mesh. Is this the sole strategy? Aren’t we missing another characteristic of the climate system: its ability to destroy and generate information at the macroscopic scale? Paleoclimatologists consider that much of this information is present in palaeoclimate archives. It is therefore natural to build climate models such as to get the most of these archives. The strategy proposed here is based on Bayesian statistics and low-order non-linear dynamical systems, in a modelling approach that explicitly includes the effects of uncertainties. Its practical interest is illustrated through the problem of the timing of the next great glaciation. Is glacial inception overdue, or do we need to wait for another 50,000 years before ice caps grow again? Our results indicate a glaciation inception in 50,000 years.
That GCMs are of no predictive value on a local basis is scarcely a surprise. What is disturbing is that, even at continental and global scales, they fail to hindcast with any accuracy, beyond vague zonal agreement. This shows that the climate simulation problem has been ill-posed, as several others have pointed out here. Behind much nonsensical talk of “positive feedbacks” and “tipping points” lurk fundamental physical misconceptions of system power-fluxes and stabilization mechanisms in a greenhouse atmosphere.
First and foremost is the apparent failure to recognize the difference between theoretical radiative capacity and actual energetic content. With highly variable water vapor accounting for ~80% of the broad-band atmospheric absorption and providing a wide “escape” window, the sharp but narrow 15 micron CO2 band (nearly saturated even at pre-industrial levels) is scarcely the controling radiative factor. Where the “sophisticated” explanation of the greenhouse effect goes awry is in presuming that any increase in radiative capacity “forces” the Earth to heat up in order to compensate for increased downward radiation by raising the power escaping through the window. But this wrongly assumes that no other means are available to cool the surface. In effect this rationale embraces a minimum entropy path, instead of the realistic one of balancing downward radiation via evaporative/convective cooling. That these two terms balance over climatic time scales has been known to bona fide climatologists for a century! This a consequence of radiative equilibrium not being sufficient to ensure thermodynamic equilibrium.
It seems GCMs adress this fundamental disparity in an ad hoc instead of systematic fashion, cheerfully producing numbers on supercomputers that have little relation to reality.
John S brilliantly said … Where the “sophisticated” explanation of the greenhouse effect goes awry is … In effect this rationale ’embraces’ a minimum entropy path …”. Entropy can not be ’embraced’ or minimally manipulated. No?
I am NO authority on entropy, but I know my entropy is decreasing, my Chem. teacher told me so. To me, entropy is a rather invisible phenomena, but explains why things relate as they do.
He also told me that entropy was a universal phenomenon. Makes sense to me that entropy indeed plays a role with our climate and our surface geology in some way.
Sophmore question
I have a bad feeling that I don’t know if my entropy is, in fact, decreasing, or do I have it backwards. Is my entropy increasing?
Turning Red, but it was over 20 yrs ago.
This thing is worthless and a complete waste of time .
I have wasted a full hour on it .
.
Resumee :
– you postulate that the “climate” dynamics at a 1000 years scale has a phase space of dimension 3 .(NB : Why 3 ? Because if it was less then the ad hoc fitting would be too obvious and if it was more you couldn’t easily draw “orbits” on a sheet of paper that has 2D)
– you pick up for the 3 dimensions X , Y and CO2 concentration . (You could add Z but then the phase space would be of dimension 4 what is forbidden , see postulate above . You could substitute Z to the CO2 concentration but then nobody would be interested)
– you write that the dynamics of each state variable is a sum of everything you can think of – a drift , a relaxation term , a temperature dependent term and , to be sure that you don’t forget anything , a random term .
– as you have no clue about what the temperature control variable (here taken as GMT) is , you must begin to fit . This is done by “Replacing the GMT by the linear approximation , the coefficients of which are estimated by general circulation model experiments” (sic !)
(NB : So the GCM runs are now considered as experimental evidence . The christian charity forbids the authors to tell us with WHAT GCM they adjusted this “experimental” fit )
– you produce orbits and feign to be surprised that they exhibit pseudo periodic behaviour that looks qualitatively like what is more or less inferred from data .
– after some trivial Bayesian considerations you come to the insight that if you have no model then the observation of the past doesn’t give you any information about the future . This insight must have appeared so revolutionnary for the authors that they highlighted it .
– you conclude that “Along with the fact that paleoclimate data have to be interpreted and retrieved by skillful field scientists their analysis turns out to be a truly multidisciplinary experience . The exceptionnally difficult challenges so posed are definitively at the frontier of knowledge .” (Quote)
– Throw in 92 references to justify the waste of time .
.
WOW !
For the completeness of the discussion and historical precision, the changing means interpretation was proposed by Vit Klemes in 1974 (Klemes, V. The Hurst phenomenon: A puzzle?, Water Resour. Res., 10(4) 675-688, 1974; see also slide 20 in the EGU 2008 presentation by Koutsoyiannis and Cohn mentioned elsewhere in this thread). My contribution is the multi-scale setting of changes and the emphasis on the stationarity of the resulting process in an attempt to reconcile the changing means interpretation with the stationary Hurst-Kolmogorov (or FGN if you wish) stochastic process.
Dr. Re: K. Hamed (#93):
Dr. H, thanks for this. I do not think it conflicts with maximum entropy at all. Rather, from first glance it seems to be in full accordance, given that there is no preferred scale.
And congratulations for producing your own Hockey stick! Have you thought of your own climate model too? You need just one step, to extrapolate to the next 100 or 500 years. Not very difficult. Two in one. 🙂 (If I remember well, David Stockwell has done such extrapolation in his blog a few years ago).
I get your point. I guess I should have not mentioned “the process” altogether. I was trying to investigate Dr.K’s notion of “lack of memory” and its ability to generate LTP-like series with all the other side effects. As I said, that was a naiive implementation of the idea, I was not implying that this is a model for climate system at all, although I now see that I may have given that impression by using the HS as an example and mentioning “the process”.
The argument that
is actually the same in the case of this naiive implementation as I mentioned
If I can’t measure it from limited data, I cannot say that it is stationary.
In the “climate-science” milieu, where trend + noise is the customary view of data, the present discussion of chaotic trajectories in nonlinear systems is a very welcome antidote to analytic blinders. That said, I’m not sure, however, that chaos and LTP formalisms are necessarily the best way to study temperature, or other natural time-series. Since weather is the physical basis of climate, and the excitation of the geosystem is a diurnal half-wave of insolation, much of climatic phenomenology is susceptible to adequate first-cut treatment via linear system theory. Thus questions of “memory” and persistence are answered by looking at system impulse response characteristics and auto-(cross-)correlation functions as well as their Fourier transforms.
It is not difficult to determine, for example, that the effective time-constant of the atmospheric greenhouse is < 0.5da, whereas annual mean temperatures have most of the spectral power concentrated at frequencies well below that of the Wolfe sunspot cycle (~11yrs). A frequency-domain wiew is often more instructive than the more-easily accessible time domain–even when considering matters of system stability (e.g., Nyquist criterion).
Re: John S. (#99),
LAnd surface air temperatures, yes. Ocean heat content, no.
Desperately trying to keep hold of this thread, as interesting.
Tom Vonk, it would help me if you explained what you mean by ‘topology’,
do you mean ‘phase space’?
Some of my modest offerings are here (but search on LTP).
http://landshape.org/enm/more-experiments-with-random-series-2
(fractional differencing and alternating means)
http://landshape.org/enm/aig-article/
(HS from LTP series, not peer reviewed)
Re: David Stockwell (#104):
I think its time for a distraction. 😉
Climate Chaos: Your Health at Risk What You Can Do to Protect Yourself and Your Family (Public Health) (Hardcover); http://www.amazon.com/gp/product/ref=pe_31770_10230020_as_img_1/?ASIN=0275998584
From the Editorial Reviews:
‘Finally, a book that spells out in compelling detail what true health–personal and planetary–means in a 21st century dominated by global warming. If you read only one book about the climate crisis this year, this is the book.’ – Mike Tidwell, Author, The Ravaging Tide: Strange Weather, Future Katrinas, and the Coming Death of America’s Coastal Cities.
Re: David Stockwell (#104),
“Topology” is the shape of the attractor. Phase space is the volume occupied by the attractor.
Re: David Stockwell (#104),
And Bender # 114
.
Indeed when I am talking about a topological invariant I am talking about the “shape of the attractor” .
As the studies of dynamical systems happen in the phase space , we are talking about trajectories (sets of points in the phase space) for time intervals .
The use of Poincarre section allows to transform a continuous process in a discrete process making the study of the dynamics easier when one looks for limite cycles of the continuous trajectories because they translate in fixed points in the Poincare section .
Now while it is both intuitive and very easy to find Poincare sections for phase spaces of low dimensions (solar system , pendulum etc) it is highly non trivial for phase spaces of high dimensions what means that discretisation is not easy for systems like the climate .
.
A GCM’s phase space has typically a dimension of several millions .
Given the standard (euclidian) metrics of the phase space you are interested in “non wandering sets” of the phase space which can be understood as volumes with several millions of dimensions that have a topological property that every orbit starting in the set stays in the set .
(Caveat : this set being invariant for a certain time doesn’t imply that it is stable forever . Indeed it sometimes is not but obeys to complex attractor creation/destruction processes through bifurcations) .
.
Observation of the Earth’s system over some billions of years suggests that :
a) such sets exist
b) are stable and perhaps even asymptotically stable
c) are chaotic (orbits are bounded but non periodic)
.
A GCM can be interpreted as 1 million of molecules (cells) with each having its set of dynamical variables (position , momentum , temperature , density etc) . The product of both numbers is the dimension of the phase space and the state of the system is uniquely defined by a point in the phase space . Considering a time series consists of doing 3 things :
– project the point on the hyperplane of one variable (f.ex temperature) what gives a vector of 1 million components (local temperatures) .
– transform this vector in a scalar by taking its norm , the average of its components (gives GMT) , whatever
– sample these scalars for different times .
To the first it can be said that by projecting the system on one particular plane , 90% of the information goes lost .
To the second it can be said that unicity goes lost because the transformation is not a bijection (an infinity of different dynamical states has the same norm or average)
To the third it can be said that if time averages are considered somewhere along the road , ergodicity is necessary .
It seems to me that it would be a miracle if after such a massive reduction of several millions of phase space coordinates , all relevant and interacting , to ONE scalar , one could extract anything meaningful about the dynamical orbits of the system from the time “behaviour” of such a scalar .
However if there is an attractor , then the projection of the attractor on some hyperplane is also an attractor .
And that’s why I said that the only thing that a study of a time series could give is a warbled , incomplete insight in the topology/shape of the attractor (which is all but stochastical !) in a particular direction (f.ex the one of the “temperature vector”) .
“Scientists around the world are in agreement that global warming, more aptly named climate change, is occurring and human activity is the primary cause.”
I wish I had become a dentist.
Re: David Stockwell (#106)
I have not read the book, but I would not be surprised if it predicted worsening of dental diseases. So, dentist may be good, indeed.
Take care…
Re: David Stockwell (#106),
Two questions…
1. Does he cite borehole data obtained by drilling root canals?, and…
2. Why am I reminded of the Rocky Horror Picture Show?
ps. apologies for OT posting.
LOL.
Bender (re: #100),
Yes, I was referring to land-surface temperatures. No, I’m not oblivious to the importance of heat in the oceans, whose upper few meters have as much heat capacity as the entire atmosphere. And more than a meter of the upper ocean evaporates each year, thereby providing strong thermal counterbalance to IR that it absorbs so strongly. But, there are no reliable century-long annual-average time series available of oceanic temperatures to provide clear spectral indication of multidecadal variability. Series reconstructed from ship-borne SST observations for intake by climate modelers and mappers are worth IMHO a bucket of skepticism. Some island stations do show a pre-eminent spectral peak near the Wolfe-cycle (~11yrs) frequency, but not consistently enough for any pronouncements from Olympian heights. Perhaps, at a lower elevation, we could agree on many things.
I’m definitely with you in the insistence that a proper ensemble consists of realizations of the same process with the same initial and boundary conditions, not just some aggregate of computer runs by different models. But, we won’t see that, because all GCMs deterministically parameterize evaporation and convection–the very processes that give rise to chaotic system behavior. Running such a model with the same inputs produces the same output (barring possibly different round-off errors). Customary modelers’ appeals to ergodicity thus seem illegitimate.
My #110 post should read: “substantially the same initial and boundary conditions.”
The question of the stationarity of f-inverse noise might be illuminated by considering a Poisson process of level-shifting between, say, +1 and -1. This well-known process is zero-mean and stationary, with an analytically-known autocorrelation function. Its spectrum peaks at f = 0. Thus we have very high power-density at the lowest frequencies–without any trends or any true non-stationarities of mean. It is only from the limited perspective of very short records that the mean of the process appears to be nonstationary.
When prefacing a comment using the handy “reply and paste link” function, it does not necessarily mean the writer is directly addressing that person. For me it is simply a handy device to indicate to readers how the thread is constructed.
Re: bender (#115),
And by the way, the numbers yyyyy in the href string “#comment-yyyyyy” somehow prevent the preview of the comment, although it posts correctly. Does any body have the same problem? I cannot preview tex equations either.
The discussions seem to have swayed a tad from the original paper and LTP.
Time to chill and have a drink.
Again, thanks to you all. This is more scientific than I can handle.
Have a round, on me, of drinks for the house (no tequilla).
Don’t tell no one, but I have actually become deluded into thinking that some of this $hit is starting to make sense.
Re: EJ (#117),
All good discussions “sway a tad” as they seek to solve a problem and reason through a solution’s implications.
To close the loop somewhat, we have learned that (1) LTP is important in climatology and climate modeling, (2) that it takes many forms that vary in recognizability depending on whether you are a statistician or a physicist or a mathematician or a topologist or a climatologist or a hydrologist, etc., (3) that understanding DrK’s other papers is critical for understanding why this one, despite its limitations, is important. Ignore them and you are in ignorant denial about the problem.
The most important lesson I have learned from the side-discussion of HK pragmaticity, thermodynamics, stationarity, topology, is that LTP is a real, practical problem, because it implies that the statistical model used for “estimating” forcing effects makes an unjustified assumption about error distributions being i.i.d. If they are in fact LTP, not i.i.d., then what are the consequences? This is an open question that should interest serious climatologists, and IPCC. Has anyone studied this? If so, is that work known to IPCC?
Getting back to McKitrick’s point in #24 in the previous thread
Indeed. Who was responsible? What were their reasons? The discussion here suggests to me that this question is more important than ever.
At the heart of the debate is weather (noise) vs. climate (signal). When the formal distinction between climate and weather is “what you expect” vs “what you get”, I am not encouraged. This false dichotomy, which would have disgusted Mandelbrot, indicates LTP denial. I think that is important. DrK’s work seems to indicate an awareness that is not present in all parts of the community. I am willing to be proven wrong.
Re: bender (#118), IMHO, you have provided an accurate and useful summation of where things seem to be. Thanks!
DrK,
How might these insights apply to something like the deep ocean circulation, which is not all that well understood? Is pointwise ocean temperature a (somewhat) cumulative process? Given that oceans are a source of water vapour, cloud buildup, and heat loss to space, is it not an open system, rather than a closed system, thus making its internal dynamics (LTP behavior) somewhat hard to infer from observations? Especially if the various ocean basins are under-sampled?
Apologies if my questions are ill-posed.
Re: bender (#123),
I do not think that I am prepared to reply your question. I wish I will do something in the future. I think simple HK processes may not be appropriate for some phenomena like ENSO, which indicate a type of antipersistence. While an HK process with H smaller than 0.5 is antipersistent, the type of antipersistence it implies is not physically realistic, as its autocorrelation is negative for all lags, whereas natural processes have positive autocorrelations for small lags. Therefore, I think that the HK process is appropriate only for natural processes with persistense.
The cumulative processes I described just above are mathematical objects, and do not apply strictly in nature. As I have explained earlier (#83), natural cumulative processes need not be nonstationary because of boundaries or losses. This makes them easier to handle as the obstacle of nonstationarity is automatically removed.
Re: Demetris Koutsoyiannis (#124), I was thinking more THC – as opposed to surface-dominated patterns such as ENSO – but thank you for contemplating the question.
Being an agenda-driven, political body, IPPC’s trajectory in the phase space of public opinion is quite predictable: CO2 concentration is the attractor (especially of multi-billion research funds) that ultimately governs system behavior. All of our ruminations about natural LTP in coupled dynamical sytems can scarcely inject a single calorie into the sangfroid of that pursuit. It wouldn’t surprise me if natural LTP doesn’t wind up being attributed, via some novel formalism, to the longevity of CO2 in the atmosphere.
It will take nothing less than stark, unmistakable exposure of the faulty physics of minimum entropy climate-system modeling, with power-multiplying feebacks from an imputed gray-body atmosphere hanging like an IR mirror in the sky, to quell pseudoscientific alarmism. But this requires a rigorous solution to the long-standing moist convection problem–no small feat, even ignoring the episodic on-off disturbances brought about by precipitation. Until then, despite some progress in recognizing the shortcomings of Schwarzchild-Milne, the sheer inpenetrabilty of GCM runs will obscure the light, like a sulphurous cloud hovering over a fledgling science.
Dr. K’s fine tutorial (#122) might become more accessible to a wider audience by remembering that physical systems have a transient, rather than infinite, impulse response. Thus, their memory is finite.
It may be worthwhile to note the new paper by Dr. Tsonis “On the variability of ENSO at millennial timescales” in relation to LTP (here).
Abstract
Wow. “This is an important result indicating that either ENSO state can persist (or dominate) over the tropical Pacific for centuries”. I hope Steve got a chance to talk to Dr. Tsonis in Erice.
I guess for Steve there is no paper explaining the 2 degrees of warming for doubling of CO2.
http://www.realclimate.org/index.php/archives/2008/09/simple-question-simple-answer-no/
Re: icman (#130), That post does not answer Steve’s call for a comprehensive, lengthy explanation for how a doubling of CO2 leads to n degrees of warming. Weart sets up a straw man and knocks it down with gusto and vigor.
Hi Not sure:
I didn’t say that it did, I said they are admiting there is no paper explaining the 2 degrees sensitivity that Steve is seeking.
Re: abstract in #129
Wow, indeed! With the paper behind a pay-wall, one cannot be sure what measurements (coral growth???) Tsonis considers to be an 11,000-yr proxy for ENSO, but almost certainly the calibration period is < 50yrs, i.e., < 0.5% of the total time-frame. And who knows what anti-aliasing measures (if any) were taken in constructing the proxy series purportedly showing significant autocorrelation at semi-millenial scales. But I’m willing to bet a bottle of Chateau Petrus (2002) that it would not show squared coherence > 0.9 for most of the frequency range upon cross-spectrum analysis with any bona fide ENSO series. In short, proxies always remain proxies and, unless one succumbs to the academic disease of mistaking idea for reality, their behavior over uncalibrated scales cannot be presumed to mimic the variable of interest.
http://blogs.theaustralian.news.com.au/letters/index.php/theaustralian/comments/ipcc_has_the_most_rigorous_assessment_on_earth
I used to be proud to be an Aussie. That pride has been diminished by clowns like this.
regards
Hi John S. (#133),
Anyone who’s collecting Chatuea Petrus shouldn’t need to worry about paying US$ 9 for enlightenment. (Of course, the 2002 is still rather young).
However that may be, the proxy record is from Rodbell (1999, Science, vol. 283, p. 516) “An ~15,000-Year Record of El Niño-Driven Alluviation in Southwestern Ecuador”, which is a “a high-resolution record of storm-derived clastic sedimentation that spans the past 15,000 years and appears to record El Niño events”, along with the follow up by Moy, 2002, Nature, vol. 420, p. 162, “Variability of El Niño/Southern Oscillation activity at millennial timescales during the Holocene epoch”.
The mechanisn is described in Rodbell as follows: “Debris flows have deposited inorganic laminae in an alpine lake that is 75 kilometers east of the PaciÞc Ocean, in Ecuador. These storm-induced events were dated by radiocarbon, and the age of laminae that are less than 200 years old matches the historic record of El Niño events”. This is based on a color identification method of carbon levels, decribed in other journals this way: “Sediment colour records can be extracted from digital images of sediment core surfaces, which provide the spatial resolution needed to measure colour in laminated sediments”.
They claim good agreement with the “known” ENSO record: “Analysis of the gray-scale record of the past 660 calendar years (Fig. 2) confirms that the clastic layers reflect El Niño events (15) and depositional events with longer periodicities”. Further “The sediment record from 1800 to 1976 A.D. reveals a close match (Fig. 3C) between the timing of clastic laminae (low gray-scale value) and moderate to severe El Niño events (6). We estimated that the age uncertainty for this part of the record is ≥5% of the age of laminae”.
I’d be happy to split the Petrus in 5-10 years.
Geoff (re: #135),
Betting a fine wine is not the same as collecting it–let alone drinking it prematurely. And now that it’s apparent that the ocean temperature proxy is nothing more intimate than the sediment color from an alpine lake in Ecuador, I’m willing to up my original bet to a bottle of Petrus of more venerable vintage.
With “calibration” apparently amounting to nothing more than a visual “close match” with the timing of reports of “moderate to severe El Nino events” and with dating uncertainties ~5%, any calculation of the sample acf on a quasi-millenial scale is burdened with more than the usual problems, which make empirical estimation of the Hurst parameter difficult in the first place. I suspect the claimed correlation is based on a much simpler computation, with scant rigorous connection to LTP. Furthermore, precipitation in this region has a bimodal annual regime, with maxima in April and October. Thus sampling at an annual rate aliases the semiannual components into frequencies near zero. This totally destroys the credibilty of any long-term variations apparent in the annual series.
Such “science” deserves nothing more than hard cider from a screw-top jug. Petrus awaits a more momentous occasion.
Re: John S. (#138), I’m not sure I understand your concern. Wang and Tsonis (WT for short) describe their proxy data and offer a reasonable explanation for why the data might reflect ENSO conditions (this is not my area of expertise; but the explanation seems reasonable to me):
If we take their assumptions at face value, then the question becomes one of statistical analysis. In particular, I am not sure I understand what you mean by:
Is it your view that the WT method for estimating the spectrum is not robust against small errors in timing or “calibration”? It seems the WT method includes steps to address issues related to poor calibration:
They also directly address this concern:
In conclusion, it is not obvious to me that one can summarily dismiss either the WT data or the WT approach, at least for the purpose at hand (recovering the H-K characteristics of ENSO).
However, I would be happy to be corrected on this point.
😉
Re: TAC (#139), My concern is, as stated in #133, two-fold: 1) proper benchmarking/calibration of the proxy variable and 2)proper construction/analysis of the proxy annual series.
On physical grounds alone, quasi-periodic precipitation-driven sedimentation of an alpine lake is unlikely to mimic non-periodic ENSO in many crucial respects, most of all: the lake is not subject to the various factors of oceanic circulation. Correlations even between local temperature and rainfall tend to be quite tenuos and vary enormously in mountainous areas. Thus my bet that cross-spectrum analysis would not show the uniformly high coherence throughout a wide frequency-range that is required for a credible proxy. That some authors are inclined to accept this ENSO proxy without such a test is for them to explain.
Persistence in time-series is essentially a matter of correlation length. Nothing is as persistent as a periodic process, whose correlation length is infinite. Thus it becomes imperative to properly filter the analog signal in constructing the annual series, in order to avoid aliasing the (semi-annual in our case) cycle of the proxy into the lowest frequencies of the spectrum. With dating uncertainties as high as 5% introducing non-descript phase modulation, this cannot be accomplished with any accuracy. The usual practice in paleoclimatology is to ignore aliasing. Furthermore, au courant resort to direct-transform (FFT) methods of spectrum analysis implicitly substitutes the circular version of the acf for the proper (non-circular) one, which few compute via algorithms (Blackman-Tukey is not one of them) that ensure that the function is mathematically positive definite.
In summary, sound science requires more than just the asertion of an idea. It requires proof. Whatever may have been shown about the persistence of lake sedimentation cannot be be accepted at face values as showing us much of anything about ENSO. I hope this clarifies my reservations, which I don’t have time to elaborate any further.
A new application of the same climate model testing methodology has been done by Marcel Severijnen in the Netherlands. Marcel Severijnen, until recently was head of the Environmental Monitoring Department of the Province of Limburg in the Netherlands, as he writes in http://climatesci.org/2008/08/06/guest-weblog-by-marcel-severijnen/, a guest post in Roger Pielke Sr.’s Climate Science weblog.
He applied the test with the data from the oldest station in Holland (or one of the oldest), de Bilt. His results are similar as in Koutsoyiannis et al. (2008) as you can see in http://klimaat.web-log.nl/klimaat/2008/09/modellen-en-vro.html (perhaps with a little help from Google Translate). Because de Bilt was very close to a grid point of the GCM he inspected, there was no need to do an interpolation at all, as he explains.
Re: Arno Arrak (#143):
Arno, thanks for this very useful comment. The book must be very interesting. I found two book reviews in Professional Geographer (http://www.informaworld.com/smpp/section?content=a789658150&fulltext=713240929) and in AGU Eos (http://www.agu.org/pubs/crossref/2007/2007EO210013.shtml). The second one concludes with this impressive suggestion/caution (!!!):
As an antidote to this caution I would like to offer the following quotations by Jakob Bernoulli [Ars Conjectandi, 1684-1689, published in 1713; quoted from von Collani, 2006: Jacob Bernoulli Deciphered, Bernoulli News, 13 (2), http://isi.cbs.nl/Bnews/06b/index.html%5D:
These I used a week ago in my presentation in Capri entitled From climate certainties to climate stochastics (http://www.itia.ntua.gr/en/docinfo/880/).
Further to my comment #142 above, I would like also to draw attention to an additional post by Marcel Severijne, in which he tested also rainfall measurements against model predictions in de Bilt, the Netherlands – with similar conclusions. Other interesting posts by Marcel Severijne include http://klimaat.web-log.nl/klimaat/2008/10/regionale-klima.html (an introduction to regional climate models and some astonishing comments from IPCC AR4 lead-authors) and http://klimaat.web-log.nl/klimaat/2008/10/fossiele-blader.html (on the relation between fossil leaves and CO2).
Finally, I would like to suggest seeing an article published in the last week issue of Eos by Rasmus Benestad entitled A Simple Test for Changes in Statistical Distributions (http://www.agu.org/journals/eo/eo0841/2008EO410002.pdf). The test he discusses is based on a null hypothesis of an iid process and he concludes:
I found it good that Benestad did this clarification. My question is why bother in studying/publishing yet another test about iid given that the independence hypothesis is just not applicable to nature.
Re: Demetris Koutsoyiannis (#144),
Good one. Slide 11, they claimed to explain anything and everything by their theories , where’s Popper when you need him 😉
re http://www.climateaudit.org/?p=3361#comment-292113 ,
I predicted
% Year Month -2 sigma Predict. +2 sigma
2008 8 0.15206 0.34864 0.54521
2008 9 0.1141 0.33388 0.55365
2008 10 0.094005 0.32581 0.55762
and observations today are
2008/08 0.384
2008/09 0.371
2008/10 0.440
Who said weather cannot be predicted beyond a couple of weeks?
Re: UC (#148),
You are doing stochastic prediction. Stochastic prediction is different from deterministic prediction and is always possible (but involves broad uncertainty bands), while deterministic prediction is good only for small time horizons, for which it involves lower uncertainty. In engineering, when we design a bridge, for example, that should resist floods for say 100 years (during its lifetime) we do stochastic prediction of floods (fortunately, the IPCC approach assuming deterministic predictability for 100 years and more has not been adopted yet in such designs). I think this is also implied by Bernoulli who identifies the “Science of Prediction” with “Stochastics” also adding “In this alone consists all the wisdom of the Philosopher and the prudence of the Statesman.”
In Koutsoyiannis (2008, http://www.itia.ntua.gr/en/docinfo/18/) I have proposed a systematic method to condition stochastic prediction on past observations of any length and for any type of dependence. In Castalia, http://www.itia.ntua.gr/en/softinfo/2/ my colleagues and I have implemented this method into software. In Koutsoyiannis, Yao and A. Georgakakos (2008, http://www.itia.ntua.gr/en/docinfo/799/) we have proposed a simple (could be implemented into a spreadsheet) stochastic method that is cyclostationary (periodic). Finally, in Koutsoyiannis, Efstratiadis and K. Georgakakos (2007, http://www.itia.ntua.gr/en/docinfo/752/) we have studied the influence of parameter uncertainty into predictions, which broadens the prediction bands.
Re: Demetris Koutsoyiannis (#144), I am curious as to whether you have had any political interest in your presentation on H-K null theorem for anthropogenic climate change?
Re: John F. Pittman (#149),
John, I do not understand this term; could you please explain?
No, I am not involved in any political interests, if I understand your connotation. On the other hand, I do have interest on political issues and I am not apathetic to political problems that greatly influence our lives. One’s world view necessarily includes elements related to the society and politics. More in my colleagues’ and mine new paper that is currently under discussion in http://www.hydrol-earth-syst-sci-discuss.net/5/2927/2008/hessd-5-2927-2008.html (Hydrology and Earth System Sciences is a top hydrological journal with open access and open review).
Re: Demetris Koutsoyiannis (#151), Sorry for being unclear. It was shorthand for if one were to propose as a hypothesis that anthropogenic CO2 was the cause of global warming, it appears that the work you show in http://www.itia.ntua.gr/en/docinfo/880/ would indicate the null theory (CO2 was not the cause of GW) was equally valid. I was in a hurry, and was not very informative.
I was also curious if the politicians had shown interest in your work. I was not trying to imply that you are politically motivated or concerned.
Re: John F. Pittman (#152),
John, thanks for the clarification. My reply now is that I have not seen any interest from politicians in this presentation (but I have seen that the paper discussed in this thread was also discussed in some political blogs).
Missing link in the above comment for the first Marcel Severijne’s post:
http://klimaat.web-log.nl/klimaat/2008/10/nog-eens-modell.html
Since all the excitement about Santer and Mann seems to have hit a brief lull, I thought this would be a good time to bump the latest presentation by Dr. K., listed above in comment #144.
http://www.itia.ntua.gr/en/docinfo/880/
It looks like it brings together much of his recent work into a single lecture format, giving quite a nice overview of key points. The presentation includes some bold statements regarding hydrology and climate modelling, which makes for an interesting read 🙂
thanks for giving me fact, it such a good blog, always keep in touch
I have a rough draft of discussion about application of the Hurst Coefficient to (1) solutions of the Lorenz equations, (2) measured temperature data, and (3) results from calcuations with GCMs. I would like to get some peer-review.
The post is here. I think you can get directly to the draft here.
Thanks in advance.
re #148 fourth successful prediction, excellent model 🙂
http://signals.auditblogs.com/2008/12/15/predicting-temperatures/
re #150
Yes, and I could add CO2 as exogenous variable in my model to include at least some physics. But now (and maybe for a while) this serves as a H0, a model that doesn’t need anthropogenic forcings.
Re: UC (#155),
This is fine, congratulations! An exogenous input re. CO2 would be also fine to add — see the last paragraph in the conclusions of the paper discussed in this thread.
If you call adding the exogenous variable (i.e. describing the correlation with one input) as “physics” then you may agree that describing the autocorrelation is also “physics”. In this case, you could replace your formulation “at least some physics” with “some additional physics”.
Even in processes without autocorrelation or dependence, probabilistic descriptions are physical descriptions. See for instance an excellent book by Keith Stowe, “An Introduction to Thermodynamics and Statistical Mechanics” Cambridge, 2007. Probability may be a difficult concept to assimilate but enhances our understanding and description of physics.
Conclusion: Probability and stochastics ARE physics.
Demetris,
Hmm, for example in the equation of #45 , with the first term in the right hand side, we have “some physics”. If we remove that term (make it unknown to us) , and just observe the statistical properties of historical position, and make a prediction based on just those properties, we’ll have a prediction without physics.
Let me put this in Meehl’s way,
Who is likely to make better predictions of future temperatures — the climatologist who knows the physics behind A-CO2, or the statistician who has only historical data at his disposal, but knows how to arrange them in a mathematical formula that will provide a predictive answer? 🙂
What I’m really looking here is a monthly prediction of future temperatures that include physics behind CO2. That must be better than my prediction. Let it even be conditional on future CO2-levels, I’ll accept that. And dodging this by “predictions over a period as short as N years are not possible”, that’s just plain nonsense..
re # 155
HadCRUT nh+sh Dec value is 0.307, first time the observation falls below my prediction :
Half-integrated noise model was discussed also here some time ago. Let’s see, CO2 should take over soon..
Jan-Feb from hadcrut3 nh+sh
2009/01 0.375
2009/02 0.345
my prediction:
Still good. I’ve discussed about this model with Hu via email, it might need some tuning ( assumes zero-anomaly before 1900) , but on the other hand, If It Works, Don’t Fix It! 🙂
Last night TAC and I attended the Darcy Medal Lecture at the European Geosciences Union General Assembly in Vienna, Austria where the 2009 Darcy Medal was awarded to Demetris Koutsoyiannis. The Darcy Medal is presented annually to an individual in recognition of their outstanding scientific contributions in water resources research and water resources engineering and management. In Demetris’ case, it was for his work on techniques for quantifying the uncertainty associated with complex stochastic processes and, in particular, his work on long memory processes that is remarkable both for its intellectual elegance and practical significance. Demetris’ lecture, entitled “A Random Walk on Water,” challenged the audience to reconsider the traditional notion of randomness and uncertainty wherein natural phenomena are separated into two mutually exclusive components, random or stochastic, and deterministic. Within this dichotomous logic, the deterministic part supposedly represents cause-effect relationships and, thus, is physics and science (the “good”), and randomness has little relationship with science and no relationship with understanding (the “evil”). Demetris argues that by admitting that uncertainty is an intrinsic property of nature; that causality implies dependence of natural processes in time, thus suggesting predictability; and that even the tiniest uncertainty (e.g., in initial conditions) may result in unpredictability after a certain time horizon, it is possible to shape a stochastic representation of natural processes. In such a representation, predictability (suggested by deterministic laws) and unpredictability (randomness) coexist and are not separable or additive components. Deciding which of the two dominates is simply a matter of specifying the time horizon of the prediction. Although many in the audience undoubtedly struggled to reconcile this view of nature with the inveterate perspective that has governed scientific thinking for so long, the logic and clarity of Demetris’ presentation was compelling and thought provoking. We are quite certain that Demetris has opened a door to enhanced predictive understanding through which many scientists will begin walking. For all who are interested, Demetris’ Darcy Medal Lecture is available online at http://www.itia.ntua.gr/en/docinfo/896/.
TAC and HFL
Re: HFL (#161),
Thank you for the notice. And hearty congratulations to Dr. K.
Re: HFL (#161),
Congratulations to Demetris Koutsoyiannis and thanks for your summary HFL.
Re: HFL (#161): As HFL notes, the Darcy Medal recognizes
This medal is a big deal. Of course, Koutsoyiannis deserves it; still, it is nice when things like this occur.
Congratulations to Professor Koutsoyiannis and to the European Geosciences Union.
And thanks to HFL for writing this up.
Re: HFL (#161):
HFL, I am grateful for writing this up. Your summary of the presentation is excellent and very useful–particularly because my own abstract is terribly long.
HFL and TAC, I heartily thank you for attending the lecture.
Mike, Bender, Spence_UK, Kenneth, TAC, thanks for your comments and congratulations.
Steve M., thanks for triggering/hosting all this discussion in ClimateAudit. As one may see, my talk was very much influenced by this discussion for issues such as randomness, dynamical systems and chaos, predictability of climate, Hurst-Kolmogorov and many more. I used the wonderful quotation by Willis (this is in http://www.climateaudit.org/?p=3361#comment-291922) also as a token of recognition of the entire discussion here. So, folks, thanks to all of you who have contributed to this discussion.
I have been silent (absent from discussions here) for a long time as I was working hard for several issues, including this Darcy Medal Lecture. Some of the additional products of this work, which in one or another way are related to this discussion, are:
1. A paper in collaboration with Alberto Montanari, Harry Lins and Tim Cohn, which discusses the “official” Summary of the IPCC chapter on freshwater (link: http://www.itia.ntua.gr/en/docinfo/907/). The authors of the IPCC chapter and the Summary (Kundzewicz et al.) were kind enough to reply. I disagree with many points and the overall message of the reply and I think that one or two things are not proper for a scientific dialogue. However, I find it good that there is formal scientific discussion (in the form of journal papers) between the IPCC/freshwater team and people who express criticism to their approach and reports. This is not so frequent, I think.
2. A continuation of the original paper discussed herein (Koutsoyiannis et al., 2008). By the way, the deadline for the formal discussion of this paper was over on 1 February and no one sent any discussion paper (although some had said they would). This makes us more confident on the correctness of our approach and results. In fact we heard of no substantial criticism for this paper (the points raised by RealClimate were overly weak and I replied them immediately from ClimateAudit, http://www.climateaudit.org/?p=3361#comment-287315). The follow up paper has been submitted to the same journal and a preview was presented in EGU (link: http://www.itia.ntua.gr/en/docinfo/900/). An additional link can be found in that web address for the diploma thesis of my former student and principal author of the new paper, Grigoris Anagnostopoulos, which details the results and contains lots of additional graphs and tables for 55 stations (point comparisons) worldwide plus 70 stations in the USA that allowed also a comparison on sub-continental basis (areal comparison).
3. An opinion paper in collaboration with my Itia colleagues (link http://www.itia.ntua.gr/en/docinfo/878/) which provides our views about climate, hydrology, energy, and water. In fact this is the introduction of a research proposal we submitted to the European Research Council for the development of a stochastic framework for those issues (the proposal passed the thresholds but was not selected for funding, which makes the continuation of our research very difficult).
A concluding remark about the EGU conference from which I have just returned home: I felt that in the EGU hydrological community (which by the way, owing to the democratic operation, the efforts of many colleagues, and the inspiring and effective leadership by the president Alberto Montanari and the former president Guenter Bloschl, has become the strongest EGU Division) there is an “ice-melting” and (at least local) “atmosphere warming” with respect to climate issues. I mean that in the formal sessions and (mostly) in the corridors there was criticism of the “beyond doubt” “established” “consensus” on climate. I do not feel any more to be an inauspicious minority when I say that climate predictions are totally unreliable.
We hope to organize a great “climate & hydrology” session in EGU 2010, and that many of the contributors of this blog could contribute also to this session.
Demetris
Re: Demetris Koutsoyiannis (#167), Demetris, thank you for the long reply and, again, Congratulations!
I am reassured by what you say:
Perhaps the scientific process works after all — even with respect to AGW. To paraphrase Beard, although the mills grind slowly, they grind exceedingly fine.
There are going to be some interesting books recounting this whole episode.
😉
Re: TAC (#168): Yes, I believe there is some “climate change” this year. For example, when a year ago we first presented the paper discussed in this thread, many said the models perform generally well but we mistreat them because they are just not designed to perform well in local level. This year in EGU we heard different things like: we all know that the models do not perform well, but it is the best we have. Or: we know that the models are terrible but we should not throw them away because they are the result of great efforts. Or: even the climate modellers know that their models are poor but they are funded for them and we too are funded to apply their outputs to impact studies. Also, some congratulated us for demonstrating the bad performance of models.
Even this blog reflects this “climate change”. Last year there was an intense discussion of the disagreement of models with reality at 8 locations worldwide, which we presented in our paper. This year we presented 55 stations plus a spatial integration of models and historical data from 70 stations over USA (my point #2 in the earlier comment). The spatially integrated series indicate an even worse disagreement, but no one seems to have any comment –- because it in no longer a surprise, I think.
Re: Demetris Koutsoyiannis (#169),
“Or: even the climate modellers know that their models are poor but they are funded for them and we too are funded to apply their outputs to impact studies.”
Biting my fingers to avoid piling on here.
I am working on a pub and while making hay with your 8 pub paper and also the IPCC recommendations of limitations in Kundzewicz, but do you have a title and author list for the 55 station paper, so I can slot it in?
Surely, surely, surely the blame in not on the models, but on those who do not evaluate the fitness of models for their intended purpose. Eg. I generate a set of random numbers to create a benchmark climate model, get it published and put into the intercomparison project (which should have been done BTW). Its not my fault if someone uses it to predict mating of whales or something. Also the onus is on the modellers to properly communicate the limitation of their models, but the IPCC shares your conclusions, that the models exhibit only the broad climate trends.
Re: David Stockwell (#170),
The paper is under review but you can use its preview presented in the EGU conference:
Anagnostopoulos, G. G., D. Koutsoyiannis, A. Efstratiadis, A. Christofides, and N. Mamassis, Credibility of climate predictions revisited, European Geosciences Union General Assembly 2009, Geophysical Research Abstracts, Vol. 11, 611, European Geosciences Union, Vienna, 2009 (http://www.itia.ntua.gr/en/docinfo/900/).
Re: Demetris Koutsoyiannis (#171),
Fantastic. Thanks from everyone, I’m sure.
Thanks for the link. And congrats to Willis for being quoted! (I think around p 44)
pp 40-43 should be required reading for all climate modelers.
Thanks for the update, HFL, and congratulations to Prof Koutsoyiannis on a well deserved award.
Predicted 3 years without problems :
2010 03 was tough, AGW almost kicked my prediction out..