Both Luboš and David Stockwell have drawn attention today to the distribution of digits in Hansen’s GISS, suggesting that the distribution is, to borrow an expression, a fingerprint of anthropogenic impact on the calculations.
I disagree with both Luboš and David and don’t see anything remarkable in the distribution of digits.
I don’t disagree with the distribution of digits reported by Luboš. I replicated his results as follows:
url=”http://data.giss.nasa.gov/gistemp/tabledata/GLB.Ts+dSST.txt” #monthly glb land-ocean
working=readLines(url)
temp=is.na(as.numeric(substr(working,1,4)));sum(temp)
working=working[!temp]
working=substr(working,1,65)
widths1=cbind( seq(0,60,5)+1,seq(5,65,5))
giss=array(NA,dim=c(length(working),13))
for(i in 1:13) giss[,i]= as.numeric(substr(working,widths1[i,1],widths1[i,2]))
giss=c(t(giss[,2:13]))
x= (giss%%10)
(test=tapply(!is.na(x),x,sum) )
# 0 1 2 3 4 5 6 7 8 9
# 186 173 142 140 127 170 150 148 165 147
As a simple statistic to test the deviation from a uniform distribution, I did the following:
test=test/ (length(giss)/1000)
K=length(test); mu=1000/K
sum( (test/mu- 1)^2 ) # 0.1220880
I did a Monte Carlo distribution test in a similar way (it is a different than Luboš’ test and it is this difference that accounts for the difference in results). I generated random sequences of length 1000 with sd 100 and then rounded their absolute values. I then calculated distributions of digits in the same fashion and the same statistic as above.
stat=rep(NA,1000)
for(i in 1:1000) {
x=rnorm(1000,sd=100)
y=round(abs(x))%%10
test=tapply(!is.na(y),y,sum)
stat[i]=sum((test/mu-1)^2) # 0.1278
}
This generated the following distribution. GISS was as about the 75th percentile – nothing to get excited outside Team-World.
quantile(stat)
# 0% 25% 50% 75% 100%
#0.0058 0.0610 0.0877 0.1214 0.3416
The only people who could take a different view would be Mannians who might say that this was a 75% significant (see Wahl and Ammann). But I discount that sort of Mannianism elsewhere and don’t support it against Hansen either.
Climate Audit 
187 Comments
Why is simple math like what is needed for temperature data analysis so secretive. Couldn’t whole lot of uncertainty be removed with openness.
Steve, I think I understand both Lubos and you. If you have the time, and for the many laymen visitor, could you expand upon your reservations? So many have wondered about cooking the data. Do you say that none happened?
Re: Fred Harwood (#2), There is a difference between “cooking the data” which does not always indicate human tampering (it can be algorithmic and the results match the random differences in real data), and actual human tampering.
Humans have a difficult time thinking up truly random numbers. We tend to favor certain digits over others. When subjected to the type of analysis done here (the chi-square), those favored digits stick out like sore thumbs.
You can try it yourself from the http://www.wikichecks.com/ page. Enter what you believe to be a bunch of “random” data by hand (pick numbers).
Steve’s just saying he used differing techniques, comparing to random distributions, etc. while trying to confirm the finding.
On the Benford law, see “http://msh.revues.org/docannexe10703.html”
#1. In this case, after refusing for a long time and under protest, Hansen did archive his source code, which is a mess – which is probably why he didn’t want to archive it. But, in this case, it is open and, for me, this substantially removes uncertainty on this particular issue. This is not to say that there aren’t other problems.
The trouble with getting excited about non-problems is that there’s a Cry Wolf about it and it immunizes people to other problems.
My disagreement with Lubos and David here is expressed entirely in the simulation. I don’t see anything untoward in the distribution.
Dear Steve, thanks for your common sense comments that defend, as is usual with you, the statistical insignificance of all observations, so that people don’t get carried away immediately. 😉
I agree that the limited variance combined with the absolute values (both are needed!) can cause some non-uniformities of the expectations for different digits counting 0.01 °C etc. Still, I would like to see a modified calculation, perhaps with different a priori expectations for the share of different digits, that would make the particular observed distribution to the different digits “likely”, i.e. probability greater than 1%, to say the least.
Without such a complete theory, your alternative explanation is just a possibility, and by doing David’s or mine kinds of statistics, it is still correct to say that there’s an unexplained effect in the game.
A bigger problem is the drop out of rural temp stations since the 1990s.
Dear Steve, one more question because I am not 100% sure whether I understood what you agree with and what you don’t.
Imagine that you are told that the digits 0…9 have 10% probability each. You generate 1548 random digits, and compute the average of (N_i-154.8)^2 over those 10 digits, i=0…9. (The sum of these squares divided by 10.)
Do you agree that in average, the average defined above should be 139 or so? Do you agree that the probability that it exceeds 370 is smaller than 0.5%? I just generated thousands of ensembles of 1548 digits, computed the quantity, and counted how many of them exceeded 370, and it was 0.4% of them.
In the IPCC terminology for probabilities, do you agree that this test makes it “virtually certain” that the distribution for different digits was not uniform?
Now, I agree with you that there can exist other reasons why it’s not uniform.
I am going to calculate the probability for the GISS-size deviation from the expectation for your distribution-rounding scheme using my methods. 😉
If I’m not mistaken, you cannot assume the distribution of digits, when actually referring to occurrence in nature, is expected to be uniform. I read about this somewhere that I can’t recall the details, but I think “1” is the most common digit unless there are leading zeros, of course.
Mark
Hi Steve, Thanks for replicating this very preliminary analysis. I won’t get a chance to check your code until tomorrow unfortunately. Another difference was that the numbers I used were all in the file (expected 260 per digit). I used a Chi-square test with Yates continuity modification — pretty standard.
Please note I haven’t claimed of manipulation at this stage. I want to take a closer look at where in the file the deviations are the greatest. Its possible it has something to do with low numbers too, as the format used of 0.01C results in single digits around 1940, but two significant digits elsewhere. I don’t know at this stage.
Mark, I am looking at the last digit, not the leading digit. The Benford logarithmic distribution becomes more uniform as you move down the number. The data must be many orders of magnitude for the leading digit relationship to hold. Measurement data doesn’t work on the leading digit.
Re: David Stockwell (#12), Gotcha, and yes, I agree. I suppose I should have read a little deeper than just Steve’s post and then taken my own advice! 🙂 At least I got some legitimate confirmation (from you) that what I read about the leading digits is correct, hehe.
Mark
This is how to conduct a civilised debate. Well done. A refreshing contrast to the horrid tone of, say, PZ Myers blog.
If you wanted to do forensic analysis to determine whether there had been manipulation of the numbers, start with Benford’s Law. It’s used by accountants for example to spot fudged data.
I’m not an expert in that field, but but one really doesn’t expect a uniform distribution from measurement data.
Dear Steve, I have performed your very test, with your particular prescription of rounding and deviations, and determined that it is still safely in the “extremely likely” category, see
http://cimss.ssec.wisc.edu/climatechange/globalCC/lesson9/concepts.html
that your theory doesn’t explain the data. What did I do? I calculated the distribution of digits expected from a normal distribution with SD=100, removed sign, rounding to nearest integer. In this setup, “0” is about 10% while “1” is at 10.3% and the percentage is monotonically decreasing up to “9” which is at 9.7% or so.
For 1548 random digits generated with this distribution, the predicted central representations of the digits 0-9 are
btt={154.638, 159.866, 158.591, 157.374, 155.936, 154.792, 153.299, 152.555, 150.954, 149.964}
Now, if I calculate the average (N_i-btt_i)^2 over ten digits “i” in an average collection of 1548 digits, described by the N_i histogram, it should not be shocking that the average is again close to 139 (0.9 times 154.8), just like previously: the central values have shifted by your rounding/limited_Gaussian bias but the overall fluctuations are pretty much unchanged.
Now, if I calculate (GISS_i-btt_i)^2 where
giss = {186, 178, 170, 157, 130, 170, 147, 131, 137, 142}
averaged over ten digits “i”, I obtain 310.94, which is less than 370+ we got before, for the uniform distribution, but it is still pretty large relatively to 139.
Now, I generated 10,000 collections of 1548 random digits according to the prescription above, computed all these things, and counted how many of the collections have the digit-averaged (N_i-btt_i)^2 greater than 310, much like N_i=GISS_i does, and the result is about 1.3%.
Clearly, the result has changed a bit in the right direction but if this were the full story about the standard deviations, distributions, and rounding, it would still be “extremely likely” that the theory of yours doesn’t work. Now, a 98.7% probability is not yet certainty but with the climatological standards (where they usually don’t need 5 sigma like in particle physics), it is damn tantalizing.
I can imagine that with a different model of the distributions, you can make GISS closer to the expectations than “310”, but with the uniform model as well as the model you have proposed so far, I still see a pretty strong signal here. I am afraid that your calculations of the percentiles is different from mine.
Unless I am making a mistake, my picture is very transparent and I precisely define the phenomena whose probabilities are being discussed. The probability that the deviation of a GISS-like ensemble from the (now-non-uniform) distribution for the digits exceeds the actual GISS measure, 310 in my conventions, is equal to 1.3% or so.
I don’t know where you got 25%.
David Stockwell:
I would have said this quite the opposite way: One has to go down many digits before one would expect a uniform distribution from the digit. And at least for the data file that Steve was using, many numbers are only a single digit long!
Steven’s approach is probably the best here: Were I do to it, I would start with the real distribution of temperatures, and use that to generate individual numbers rounded to the same accuracy as the tabulated data that you are using as the basis for your study.
I would then use a series of such Monte Carlo simulations with random numbers generated in this way as a starting point for analyzing whether there had been any manipulations of the input data stream.
(I would think you would get a “yes” answer if you did it carefully, because things like infilling missing data points is a form of manipulation of the data.)
Re: Carrick (#17),
I agree with Carrick on this – how can you not expect a human fingerprint on this data? He alludes to one manner that that the data is “tampered with”. But the many measurements taken by humna beings whether from buckets or thermometers, not to mention transcribing of data, conversions from F to C, and other rounding – it would be hard for me to imagine that there would be no human fingerprint on the data.
I suppose some might argue that large numbers should result in some kind of averaging of digit use, but did we not already know that data was heavily processed?
I fear this will end up as an interesting exercise, but a waste of quality talent.
Incidentally, for readers who don’t have Mathematica, here is my notebook as HTML:
http://lubos.motl.googlepages.com/giss-teploty.mht
Internet Explorer needed to view MHT files.
Isn’t the rounding error likely to be much larger in this situation than one would expect when perhaps checking someone’s expense account claims?
These figures are being quoted to 0.01°C. I doubt when sticking a bucket over the side of the ship and then reading a thermometer, they would have written down an answer any more than to the nearest degree. Mind that would probably have been in Fahrenheit in the early days. Seems to me lots of fairly similar whole numbers would be added together to create monthly totals. The average for the 1950-1980 period would then have been removed. So these values have all gone through the same sausage machine. Sum the numbers for a month, divide by the days in the month 28,29,30,31 subtract the 1951-80 average.
Mind I don’t know that that was how it was done. But, it seems likely that lots of temperature measurements returned as whole numbers have been processed in a fairly simple way, and that could easily lead to rounding errors – two digits further down.
Steve — The counts you report in the post for the last digit,
# 186 173 142 140 127 170 150 148 165 147
are not the same Lubos reports in #16, or David reports
on his blog:
186, 178, 170, 157, 130, 170, 147, 131, 137, 142
Using your counts, I get a significant deviation from uniformity using a normal approximation to the binomial probabilities:
Chisq(9) = 19.11, prob = .0243.
Using theirs, it’s even more significant:
Chisq(9) = 24.80, prob = .00322.
I doubt that there is anything sinister in the prevalence of zeros, but it’s an interesting crossword.
There are only 9 DOF, since the last count is foregone given the preceding ones. It is also important to remember that each successive digit count is drawn with an increasing probability from a decreasing pool of remaining observations. This should be equivalent to a Pearson Chi^2 GOF test for uniformity, though I haven’t checked it.
Here is my Matlab program, set to run with Lubos’s counts:
% hansen’s digits, CA 1/14/09
clear
% Steve’s counts:
m = [186 173 142 140 127 170 150 148 165 147];
% Lubos’s counts:
m = [186 178 170 157 130 170 147 131 137 142];
n = sum(m’)
ni = n*ones(1,9);
p = zeros(1,9);
em = zeros(1,9);
s = zeros(1,9);
e = zeros(1,9);
z = zeros(1,9);
z2 = zeros(1,9);
chisq = 0;
for i = 1:9
if i > 1, ni(i) = ni(i-1) – m(i-1); end
p(i) = 1/(11-i);
em(i) = p(i)*ni(i);
s(i) = sqrt(ni(i)*p(i)*(1-p(i)));
e(i) = m(i)-em(i);
z(i) = e(i)/s(i);
z2(i) = z(i)^2;
chisq = chisq+z2(i);
end
format short
m
ni
p
em_s_e_z_z2 = [em; s; e; z; z2];
em_s_e_z_z2
chisq
prob = 1-chi2cdf(chisq,9);
prob
Re: Hu McCulloch (#20),
I would tend to agree. In R you can do something after Steve’s first block of code like
or more directly
or
and get your results. I would say that even if the p-values were statistically significant (I am not convinced the first is on a two-tailed basis), for me they are are not substantial enough. I would be more concerned over Mendel’s peas results.
In some of the data the lack of the expected number of digits extends from monthly data into the related bi- and tri-monthly “calculated” averages. Not just once, but in several different time spans. What, but extreme improbability, or the hand of man, could do that?
Nick:
Er no.
Not the ones Steve is using at least. They are rounded to the nearest whole number.
Re: Carrick (#22),
Yes whole numbers of hundredths.
Also a significant proportion of the data are single digits which I would think would skew the analysis. Re: David Stockwell (#12),
Geoff:
Sounds like “infilling” of missing data points. I’m pretty sure they say someplace that they do this.
Just a thought- and, as a total technical ignoramus, please be gentle when shooting me down! It has been stated in some blogs, rightly or wrongly that the rate of GW has been exaggerated by the depression of earlier temperatures and an elevation of later temperatures. Rather than subjecting an entire annual data-set to be scrutinised under the Benford StatisticsScope, should we perhaps be better focussing on whether selective manipulation may have taken place, or not, to lay that perticular baby to rest or demand an inquest!
If I’d had an agenda like the above I would only be interested in altering data that didn’t meet the criteria I wanted.
Out of my depth on the stats but how do these test results (Steve’s) for GISS data compare to doing the same test on the other measured rather than random generated datasets? Luboš site suggests the GISS dataset under his test stands out as different? Sorry if that misses the point and the single test result is classification enough.
Speaking of significant digits and rounding, Hansen made a significant “rounding down” of global warming expectations over the past few days. This was repeated on his personal blog and on the offical GISSTemp page today.
The warming trend has been reduced to ~0.15C per decade from the previous GISS and IPCC mantra of 0.2C per decade (the actual number was higher than this but this is the figure they usually quote).
We cannot reach +3.0C of global warming by 2100 at this lower rate.
“Greenhouse gases: Annual growth rate of climate forcing by long-lived greenhouse gases (GHGs) slowed from a peak close to 0.05 W/m2 per year around 1980-85 to about 0.035 W/m2 in recent years due to slowdown of CH4 and CFC growth rates [ref. 6]. Resumed methane growth, if it continued in 2008 as in 2007, adds about 0.005 W/m2. From climate models and empirical analyses, this GHG forcing trend translates into a mean warming rate of ~0.15°C per decade. ”
http://data.giss.nasa.gov/gistemp/2008/
Click to access 20090113_Temperature.pdf
#26: Just an impression from the various comments here is that the focus is too much on whether they are significant, or by how much, rather than WHY they deviate. I wouldn’t write off an analysis like this because it is a hair above or below 0.05 probability. Far more interesting are issues like the location in the series of the peaks of deviation. If around 1940, as is suggested in preliminary analysis, there is a possible motive for manipulation, and it argues against say rounding as an explanation that would be distributed over the whole series. If its evenly distributed, then the explanation probably lies in the computational chain.
The answer to that one is going to have to wait for more analysis.
LOL, what a fun discussion. Sadistics is no less interesting than creative physics.
The “IPCC Mantra” is:
Click to access AR4WG1_Print_SPM.pdf
Hansen is stating the current rate of warming due to increasing GHG is about 0.15 degrees per decade. That is not the expected rate over the next 20 years or the next 90 years.
Please seem my comments regarding the wiki analysis and the probability of seeing 2 digits with significant @.05 deviations (same line of thought if not same original analysis – over at WuWT)
This should happen quite often, (7.5% of the time), even with purely random data (binomial distribution analysis of 2 events out of 10 with @.05).
http://wattsupwiththat.com/2009/01/14/distribution-analysis-suggests-giss-final-data-is-hand-edited/#comments
Michael D Smith (17:40:19) :
I’m interested in your take on that analysis / comment, and whether testing for the distribution of historical temperature adjustments by GISS might be more worthwhile. Ho is that for a given year, all adjustments should add to zero and / or the number adjusted up should equal the number adjusted down). (the average temperature was not affected by homogenization).
Michael, The variances of each digit (1DF) in the table don’t product directly to the significance for the whole distribution (9DFs), I think. The more reliable values are for the whole distribution chi-square result (9DFs), on the variances. I am not too sure about the individual digit significance values actually. I put them there pending more information.
My Ho is that there is no difference in the form of manipulation over the whole series (period). If there is a significant difference between distributions of digits at one period vs. another, that would be consistent with manipulations that are directed at specific times in the record.
cce–
What time period would you use to define the current period? I have downloaded the monthly data for all the IPCC models and can compute the model average trend for any period you like. If you pick a period, we can see how the model avearge trend compares to 0.15 C/decade vs. the IPCC stated trend of about 0.2 C/decades for the first two decades of this century.
Hansen owes Steve a debt of gratitude, disagreeing with Lubos and David here and finding the errors in the past.
#35 The take-home message for me would be that if the digits are shown to differ significantly from the right distribution, that would be additional evidence of the unreliability of the surface temperature records. Both GISS and CRU deviate, but the satellite records from UAH and RSS do not. Proof of non-manipulation, which has been shown already by their randomness, gives me more confidence in the satellite records.
Hmmm, my test above contains a mistake. I did the simulations with 1000 readings and “normalized” the 1548 values by dividing the distribution by 1.548. This changes the chi-squared distribution. The calculation that I did above is equivalent to:
The statistic shown here is the one that I calculated above multiplied by 100 and “normalized” is not anomalous, as I observed. However, if the distribution isn’t “normalized”, then
In a simulation similar to above but with 1548 in each sample as with GISS, the quantile for 18.89992 is between 96th and 97th. Sometimes this sort of thing happens.
stat=rep(NA,1000)
for(i in 1:1000) {
x=rnorm(N,sd=100)
y=round(abs(x))%%10
test=tapply(!is.na(y),y,sum)
stat[i]=unlist(chisq.test(test)[[1]])
#stat[i]=sum((test/mu-1)^2) # 0.1278
}
quantile(stat,seq(.9,.99,.01))
# 90% 91% 92% 93% 94% 95% 96% 97% 98% 99%
#15.54134 15.90297 16.56382 16.78217 17.25323 17.61822 18.33282 19.64935 21.44470 22.57119
Couple of quick thoughts – First, I understand the concept behind the analysis but think it is truly grasping at straws. temperatures are typically recorded to the nearest degree at 1000s of stations; each station record is subject to a variety of manipulations/adjustments; the stations are thrown together to come up with estimated values for 5×5 grid points; these grid points are then averaged to obtain a global mean surface temperature; and then, the anomaly values are calculated to the 1/1000ths of a degree. David and Lubos, why should we expect the third decimal place to be normally distributed? and who cares if the values are off by a couple of thousandths anyway. Heck, I am not sure that differences of hundredths of degrees are important. There are plenty of real and potential problems with the historic temperature record, but you better have something more solid than this if you are going to suggest deliberate data manipulation. Otherwise, it does start looking like the tin-foil hat crew.
David, you mentioned that both of the surface records deviate but the satelitte records do not. Could you elaborate on this? To what extent would this be an artifact of the many manipulation/adjustments applied to the the surface temp record.
Hi Steve and Happy new year!
It might be interesting to try to correlate these digits to the years or months . . perhaps there is some deeper structure in that data . .
All the best,
LoN
“a couple of thousandths” in the long run could make quite a difference in prediction global temperature rise. It could be the difference in having a prediction that is below earlier estimates, or a prediction that is close or fitting to the earlier made predictions.
Hi Bob, As I said on WUWT this morning and you quote rightly point out, I don’t see this impinging on AGW science as the differences are too small. So don’t misunderstand that that’s where I am coming from. To draw a parallel, see an analysis of the Canadian UBS fund data on the WikiChecks site. Would you be concerned if your mutual funds showed more 4.1’s that 3.9’s in percentage returns each quarter? Maybe not if you are an investor and its in your favor. Maybe yes you are another fund playing the game fairly any trying to compete. I am not saying at this stage that the result for GISS is intentional or cheating. It could be an artifact of the way the data are prepared, how the gaps are filled in, a hundred things. Its a pretty obvious form of analysis and you have to start somewhere.
#38. I agree. The main utility of this example may well be to show that something that is statistically anomalous isn’t the same as proving physical causation.
Hand collection at the observing stations?
Steve of all people should know better than to go off inventing new statistical tests when perfectly good standard ones already exist. Any introductory statistics student who doesn’t look at this problem and cry out “chi squared test!” hasn’t learned their material.
It took me all of two minutes to calculate chi^2=18.88 with nu=9 degrees of freedom for this data. The probability of such a high chi^2 is 2.6%, so one can say with very good confidence that these digits are not uniformly distributed.
That, however, is still a very long way off from saying with any confidence that the data have been faked, falsified, or tampered to support a conclusion. By far the biggest outlier (at 2.5 sigma, accouting for about 1/3 of the total chi^2) is the high number of zeros, which is what one expects when measurers record “round” numbers. Another clear effect is that even digits are favored, which is also a common human memory effect.
I believe I have read (but I’m too lazy to hunt for it) previous analysis of large bodies of published experimental data which have consistently found a non-uniform distribution of digits along these same lines.
Steve: I didn’t actually try to invent a new statistical test. The expression that I used is a chi-squared test, though the R-function would have been easier. What I wasn’t paying attention to is that you can’t “normalize” to 1000 by dividing by 1.548 without changing the significance. My bad, as I observed above. A somewhat off-center proportion over 1548 is obviously more unlikely the same proportion over 1000.
Re: David Wright (#44), Steve did a Monte Carlo simulation. The problem with the Chi-square test is that I have to assume a distribution, which I assume to be uniform. The Monte Carlo simulation was an attempt to remove that assumption. Turns out they agree, more-or-less.
Re: David Stockwell (#45),
You have to assume a distribution to do a Monte-Carlo, too. If you don’t assume a distribution, what do you draw your random numbers from? (If you think it doesn’t matter, try this distribution: 1, 1, 1, 1, 1, …)
There are cases where the assumptions required for standard statistical tests don’t apply, so Monte Carlo or other techniques are required. This is not one of them.
Re: David Wright (#46), Well yes you are right, but I was referring to the expected distribution in the Chi-sq test. The distribution enters at an even earlier stage in the Monte-Carlo procedure.
Statistical deviations in least digit frequency might well be a result of floating point representation and binary-decimal conversion.
What is the average and decile number of digits in the temperature series from Hansen? Is it two digits then the argument have som sway but if only one digit is given in a certain number of cases the argument is weak.
Re: avfuktare vindar (#50),
In the 40s (specifically mentioned as being significantly ‘worse’) about 60% of the entries are single digit.
Steve (#44),
If I am deciphering your R code correctly, then what you did does not reduce to a chi^2 test, even when N = 1000. You computed \sum (N_measured/N_expexted – 1)^2, but a chi^2 test computes ((N_measured – N_expected)/\sqrt{N_expected})^2. Those are simply different quantities. There are a lot of theorems about power, bias, and efficiency that pretty much guarantee that chi^2 is a better test statistic.
In any case, this is a good example of a case where simply citing the result of a standard procedure (“a chi^2 test rules out a uniform distribution of digits at the 97% confidence level”) communicates more clearly than a bunch of code.
I do admire you courage for “doing math in front of an audience,” something that working scientists know nearly always goes wrong.
Well, the effect seems to almost disappear if one uses the GISS land only data. Since GISS is using HadISST1 for the period 1880-11/1981 (Reynolds v2 afterwards; HadCRUT3 is using HadSST2), I speculate that, if there is something to this, the problem is either in the HadISST1 or in the way HadISST1 is combined with GISS land temperatures.
Re: Jean S (#52), Always liked your work Jean S. Its going to take some time to track down the source of the digit deviation, and it could well come from CRU and not GISS via component datasets, as you suggest. The sig. of the CRU data being higher supports this view.
With so many eyes on Hansen’s methodology, I at least feel reassured that he’s going to be a lot more careful with his data computations in the future. That’s good.
In the statistical discussion here it appears to me we’re dicing a few hundreths, possibly a tenth, of a degree. Yet, as Anthony Watts has shown, the real errors are not in the statistical data evaluation methodology, rather they are in the instrumentation and measurement methodology. Poor siting, poor instruments, etc. mean GIGO!
GISS is very likely working with very low grade data (garbage) to begin with. Does it really matter if the garbage is computed exactly or not? Crap is crap…no matter how exactly you quantify it.
Be it manually changed or not, their methodology for calculating “missing data” more than one century ago with averages that include present-day data is already weird enough to rise an eyebrow.
With the release of December data, a lot of long-ago monthly anomalies have been changed. The changes are very small, however I wanted to know how important they were compared with the December data itself. And I have been making numbers.
Just adding the December “real” (GISS version) data, without changing the past, would give a warming trend for 1900-2008 of +0,65574 ºC/100y. By including the modifications of the past, the new warming trend happens to be +0,65633 ºC/100y. As you can see, the warming trend change introduced by the modifications of the past history is minimal, affecting only from the 3rd significant digit.
However I decided to make the following comparison: what temperature anomaly would I have to introduce for the December data, in such a way as to obtain the same warming trend without changing the past? And this is the result: I would have to use a December anomaly of +0.59ºC instead of +0.45ºC. Which means that, as little as the changes in the past history seem to be, their effect over the overall warming trend is equivalent to increasing the December 2008 average temperature by +0,14ºC. Quite noticeable. Now imagine introducing those little changes EVERY month…
Re: Nylo (#54), That’s incredibly ridiculous. Of course that for a given 100 year’s range, a small change in the trend would need a fairly great amount in the last monthly input. That’s a tautology and a meaningless one. But please, wear that tin foil hat if it suits you.
Re: Luis Dias (#56), you didn’t get the point. What I am saying, exactly, is that the apparently minimal changes in temperature history performed by GISS this month is equivalent to a big change in this month’s temperature, in the way they affect the trend.
Do you remember the scandal of the Siberian November data carried-on from October data? Well, if it hadn’t been corrected, its warming effect over the 1900-2008 trend would have been LESS IMPORTANT than the effect caused by these lesser data corrections of the temperature history GISS just performed.
This rewritting of the past history that GISS performs has as big an influence in the trend as other big screw-ups like that of Siberia in November. And they can do it every month and few people would notice.
Re: Nylo (#57),
No, what you are doing is cherry-picking. For you to have reason on your side, you’d have to demonstrate that the overall filling-in-the-gaps average process by GISS have a statistically significant deviation towards increasing the temperature trend. Otherwise, you’re just saying that the GISS algorythm changed data as it is supposed to do.
Re: Luis Dias (#59), You are right about that, Luis. I have cherry-picked, because I only have one cherry, and it looks spoilt. I cannot deduce that the whole bag of cherries is spoilt, yet. That’s why I am asking for people having previous versions of GISS data stored to, please, tell me where I can obtain that, in order to be able to keep picking cherries to see if they are spoilt as well. It would be extremely useful, for example, to get a GISS data version of December 2000 and compare it to this of December 2008, and then see how the 2001-2008 data have changed the XX century warming trend.
(My god, it even sounds ridiculous… 2001-2008 data changing the XX century warming trend…)
Re: Nylo (#61),
Have a nice work, Nylo. Just don’t forget that statistically, it is expected that 50% of the time it will increase the average trend, while 50% will decrease. Worse than that, I could even be wrong on that statistics due to technicalities that are far above my knowledge. So even if you could show that it is above 50%, you’d still have all the work to do, in proving that it is really supposed to be 50%. Good luck. I won’t bet on you.
Re: Luis Dias (#63),
So Luis, what do you do for a living, or are you just a professional Troll?
“This is a non-sensical matter.”
“I understand the pschological need for some of you guys to “score” against GISS, Mann, Hansen, et al, at all costs,”
“That’s incredibly ridiculous.”
“But please, wear that tin foil hat if it suits you.”
“or are you all just going to cherry-pick your way to fandom blog awards?”
Such childish insults won’t get you far here. But as you say, “Good luck. I won’t bet on you.”
Re: Luis Dias (#63), you just also don’t forget that learning the world temperature of December 2008 should not change the previously recorded April 1902 temperature in any way, neither for cooling nor for warming. This is something already weird, and many people have complained in the past about this GISS procedure without getting a proper answer as to why this is done in this way. I shouldn’t be investigating if this procedure introduces a bias because, first of all, this procedure shouldn’t be done at all.
Why our knowledge of the real temperature in April 1902 should improve by learning the December 2008 temperature (different month of the year, different season, different century!) completely escapes me, unless it is a cover operation for something else, therefore highly suspicious. I wish I had the exact formulas that show how the past temperatures are influenced by the new ones in Hansen’s procedural madness. That way I would not have to guess what the previous versions of GISS data were, I would just calculate them.
This is a non-sensical matter. I’m with Steve here. I can’t believe that so many bloggers have dwelled in this idiocy. As some have pointed out, if there are any errors in GISS, whether in methodology, GIGO or whatever have you, they will be much more important to find and document than this piece of garbage inquiry that will only serve to make you look foolish in the eyes of RC’s and Tamino’s readers. Congrats for making clowns of yourselves.
Also, I can’t believe that probably the “best science blog” of 2008 is even interested in this garbage. I understand the pschological need for some of you guys to “score” against GISS, Mann, Hansen, et al, at all costs, but please, you do not need to paint yourselves as luddites and paranoid conspiracy UFO-kind of people in the process.
Two corrections to my above post.
I am referring to the September-to-October carry over of the Siberian data, not October-to-November.
And the effect, althoug similar, was more, not less, as it caused an incorrect rise of +0,2C in the October data.
Either way, it smells badly. Anthony Watts in its SurfaceStations.org is at least trying to make a scientific claim about the accuracy of the temperature stations, but alas, the report they make is completely subjective and non-quantitive. I’d like to see a good statistical analysis to what he has done there, but I have little faith that his effort will be nothing more than fuel for easy-skepticism towards the temperature stations’ data, while pretending to be more than so.
I had also a little faith that someone was looking at the algorythm of GISS with true and elevated skepticism, but alas, it seems that the end number of each monthly data is more important. It reeks of amateurism and clubism, where people just happen to see something awkward and figure out that it is a good way to unnerve and raise skeptical little minds over the whole science of it.
What a waste of time.
Will the real skeptics stand up and do a good reverse engineering of this GISS and surface stations real methodology and present an alternative, or are you all just going to cherry-pick your way to fandom blog awards? I’m starting to understand the frustration of the Team when asking of McIntyre (but it could be about any other skeptical mind) about producing real science rather than showcasing the small mistakes and errors in the other’s people work, while pretending that such mistakes are enough to destroy what they perceive as a house of cards.
Re: Luis Dias (#60),
I think Steve McIntyre doesn’t really count as a “skeptic”. I don’t think he has voiced an opinion on what is really going on with AGW. Steve is more of an auditor. Perhaps he should mention that somewhere in the title of his blog so people don’t get confused?
Re: Patrick M. (#64), I’m not confused at that, I’m particularly informed about Steve’s stance about Global Warming. I disagree with him though and think of him as a skeptic. It is enough to look at the “friends” one has in the “internets”. Say with whom you gather, I’ll say who you are. I won’t develop this further, it’s completely off topic and unwarranted and uninteresting too, for I don’t care if one is skeptical or not towards a theory. The juice is what matters.
And this current juice is pathetic (not Steve’s fault).
Re: Luis Dias (#60),
The SurfaceStations.org project is waiting until 75% of the stations have been surveyed before attempting any quantitative analysis. This has the two obvious benefits of increasing the reliability of any results and refuting objections that the data are cherry-picked. It’s a personally-funded, volunteer effort so it will take some time to complete. Your skepticism toward the motives for the project can be accepted at face value, but to be fair you should acknowledge its transparency. Anthony Watts frequently cautions against drawing premature conclusions and extrapolating beyond the data. You should too.
Re: Luis Dias (#60),
One thing I notice is that critics seem to infer motives of others based on their own prejudices. So, for example, SteveM and Lucia are deniers because they have pointed out flaws in AGW papers or data, regardless of they’re specific statements to the contrary. It says much about closed minds of true believers regardless of their positions.
Anthony is trying to survey the stations that make up the US portion of the GISS temperature data set to determine if their siting meets acceptable standards. Something the government should have done themselves. The contention is that these are quality stations that meet standards that make their data acceptable for use in climate studies. If that is not the case then it throws into question the accuracy of these climate studies. It is up to the authors of these papers to justify why badly sited stations can be used in these studies, not Mr. Watts.
He is using the governments own CRN standards for grading station siting. Yes, there is some subjectivity in the assignment of specific numbers but he has already shown that the quality assurance by the government on station siting is flawed or non existent. And he has a photo record of the siting to support his assessments. . If nothing else comes from it that is a major accomplishment for a volunteer group.
I’ve twice seen a flock of birds get drunk on rotting mulberries. I see it happens with humans and rotting cherries, too.
===============================================
I agree to a certain point with you Mr. Dias, that there are some things that are valid concerns, and others that are not. In this case, I also choose to have good faith in the data because, as McIntyre pointed out, there is really nothing out of the ordinary. Your choice of rhetoric, on the other hand, seems a bit strong.
I also have to disagree with your assessment of Mr. Watts’ work. I think it is still objective, but not quantitative. Qualitative observation is a perfectly valid method of inquiry. That he has neither the funding nor the support of the climate science community to conduct quantitative measurements of station bias should not reduce the value of his project.
Finally, I would like to point out that on ‘the other side’, most of the discussion is carried out by yes men subordinate to the writers of the blogs, and there is no room for dissent anywhere there. At least over here, you’re allowed to disagree with the people doing the calculations and criticize them when they overstep and make a mistake. I believe that a mistake was made in accusing the data in this way.
Re: Eve N. (#66),
Perhaps, but it is almost pointless nevertheless. Unless one can gather quantitative results from his work, we are left to guess the numerical consequences of his survey. Does the errors he finds mean a erroneuos trend of more than 0.5ºC? 0.05ºC? 0.005ºC? Unless one is able to gather enough quantitative data to be able to get a global view of it, it will always come down to anedoctal evidence. Which, of course, will always fuel appeals to ignorance from the part of the interested laid back.
It doesn’t reduce the obvious ambition of mr. Watts, but clearly reduces the conclusions and importance of his project. Regarding the Groupthink problem you refer, I’d like to point out that generally, that’s also expected. The status quo is always the thing to beat, so they get defensive. Other contenders like to gather enough appeal to counter the fact that they are not mainstream at all, and oppenness and correctness always served them better. And while I apreciatte this, it is completely parallel to the question of who’s right or wrong.
Re: #59
“on your side”
Sigh.
Andrew ♫
“anedoctal evidence” = people’s actual lives. Which is why the climate matters at all to begin with. Don’t be so quick to dismiss the evidence. Without anecdotal evidence, there are no “trends” built to look at. *All* of the real evidence is anecdotal. If someone reading a thermometer on a given day is anecdotal, *The Whole Thing* is anecdotal.
Andrew ♫
It’s certainly not anecdotal because the project aims to evaluate every station by the end of it. It’s methodologies are clear and are open to discussion, so it can be subject to peer review. I think the problem you’re having with it is a misunderstanding. You are demanding quantitative data from it. The question you want answered is “What is the impact of improper data gathering on the measured change in global temperature?”, but that is not the question Mr. Watts’ project is answering. He asks, “Is the data gathered from the USHCN weather station network reliable?”. The answer so far is, “There is room for doubt.”
This might not seem like a good answer because it is not hard, it is not definite, it is just a doubt. But the fact that there is evidence to doubt the data is a good conclusion. We may not know how off the data is, or if it is off at all, but the evidence introduces uncertainty into our methods. Since the survey supports the idea that maybe the sites are not properly maintained, there is reasonable cause now to do a full evaluation, maybe get some hard data, and discard the data gathered from the stations.
It is like in a court room case, where the goal is not to prove a defendant’s innocence, it is to produce doubt in his conviction. The goal is not to produce numbers, it is to answer a qualitative question. When the question is answered, then quantitative data collection can happen to either verify or contradict the hypothesis.
I understand that a lot of it has to do with group dynamics and conformism. One sees that a lot when people become emotionally attached to things that ought to be objective. On the other hand, it is also encouraged by the proprietors of ‘the other side’. If you voice dissent on RealClimate, for example, or even show the smallest inkling of respect for McIntyre’s work, your comment will be moderated and most likely surpressed.
I do not like the rhetoric of most blogs. Especially in such a politicized topic, most blogs have a rude streak that is less than admirable. But there are a few places where clean discussion can happen, and I think one of those places is here, on this blog. It’s a little difficult not to be caught in the crossfire of dung flinging elsewhere.
Anyway, like I said, I can see where you’re coming from, and agree to some extent. But then again, I think you should cut some slack for qualitative analysis. It’s not as bunk as you think it is! Every observation has to start with a qualification after all.
Re: Eve N. (#72),
Thanks for your reply. I agree 100% with Steve’s comment #75, it is this kind of game that distracts from real science or auditing going on. It’s not that people don’t like to toy up with statistics, like Ailee poorly tried to defend, but that accusations of manipulating data either were clearly stated or hinted at, so that the commenters of such blogs filled in the supposed blanks and started to shout fraud before the devil could blink the eye.
I’ll wait then. But given past examples of Watt’s statistical capabilities of misrepresenting data, I’m not exactly enthusiastic.
Re: Luis Dias (#78),
I believe SurfaceStations needs a statistically reliable regional representation in addition to the 75% sampling. You shouldn’t prejudge the output from the project. It’s unseemly.
============================================
snip – please do not respond in kind.
I think some of you need to get thicker skins and stop spitting venom whenever you feel threatened. Now this is getting off topic, I apologize.
Steve: Quite so. I expect regular readers to have good manners. I give much more leeway here to critics than “supporters”.
Re: Steve’s inline in (#74),
Indeed, and you should. That’s part of what separates you from RC: a desire to give “the other side” a fair shot at falsifying your work, without being drowned out by all those that already support your work.
Mark
#60. Luis, in the case of the reconstructions, I submit that we’re not talking about “small mistake”, though the Team treats them as such. The problems that have been identified are ones that go to the root of whether the reconstructions have any meaning.
As it happens, I also agree about this digits thing getting disproportionate airplay in the skeptic blogosphere and that the mere speed of the play shows an unbecoming partisanship – where people are looking for the slightest thing to discredit Hansen.
Unfortunately, people forget that Schmidt et al are doing exactly the same thing. They love this sort of over-stepping by critics and feast on it. They use this sort of thing in reverse – to pooh-pooh more substantive criticism.
For someone like me who thinks that there are real issues with how Team things are done, this faux controversy is very unfortunate.
Referring to Eve N. (#66), Luis Dias (#70) writes,
It is up to the claimant to prove that the claims are supported by sound data and that the methods are properly validated, not the other way around. What Andrew Watts is doing at surfacestations.org is to cast reasonable doubt about the data that the AGW scientists are using in their climate models.
Assuming that the doubt is merited, this is a service of almost inestimable value. If not, then he is still providing a service by demonstrating to the climate modelers how they might improve the presentation of their arguments. I, for one, thank him for doing something that should have been done long ago by the AGW climate modelers themselves.
#79. The Hansen adjustment code is now online (thanks largely to CA efforts. I don’t think that it’s a good idea to adjust past data the way that they do and the forms of adjustment are bizarre to say the least. But you’re over-editorializing here. I don’t think that the adjustments are a “cover” for anything – they’re just goofy mathematics. CRU does it differently and has similar results without past adjustments. Don’t misunderstand me – the constant adjusting of past data annoys the hell out of me, but I think that it’s just lousy methodology.
As I’ve written before, my take on the issues are different from the complaints of many commenters – I don’t think that Hansen’s UHI adjustment behaves very differently outside the US and is essentially random outside the US, while it accomplishes something in the US. (And my line on this has been very consistent.) The moral is therefore different from surfacestations critics draw: it may well show that the GISS adjustment works OK in the US, but it’s a bait-and-switch to extrapolate from the US example to the ROW. I’ve argued with John V about this and he says that he’s only talking about the US, but the implication is that this is relevant to the ROW. I’m more interested here in the comparisons to NOAA and CRU in the US.
Re: Steve McIntyre (#80),
Steve, I REALLY, REALLY think that you should have a look at this excel file. I have found a wonderful web page called the “Way Back Machine” from where I have been able to obtain GISSTEMP’s “GLB.Ts+dSST” data as it was available in December 2005, and I have compared it to the data available now, in January 2008. The result CONFIRMS my initially not-grounded-enough hypothesis that Hansen’s method, intentionally or not, consistently cools the past temperatures and warms the more recent historical temperatures, most probably only a little bit with every update, but with an overall huge impact after a few years of repeating the same operation.
All the cells that are shaded in a cyan color are monthly averages that have been cooled since the December 2005 GISSTEMP “GLB.Ts+dSST” version. All of the cells that are shaded in an orange color are monthly temperatures that have been warmed. Only the grey cells are monthly data which have suffered no variation. This result is overwhelmingly visual.
You can also find in the excel sheet the calculated warming trend for the period 1880-2004 (and you can also calculate it for any time period you wish). With the data available in December 2005, that trend was 0,48 ºC/century. With the data available today, the trend for the period 1880-2004 has increased to 0,53ºC/century. This has been achieved only by adding data which is OUT OF THE PERIOD whose trend we are calculating. Now you can tell me that this method introduces no bias in the trends… In only 3 years, the overwritting of historical temperatures has managed to increase the trend by 10%.
My god, I would kill for a GISSTEMP data version from 2001.
Re: Nylo (#122),
Nylo, check out this thread
http://www.climateaudit.org/?p=2964
I believe it contains much of the information you are looking for, including data from 2001.
Luis Dias,
I don’t understand your suspicion and apparent loathe for what Anthiony Watts is doing. Maybe Anthony has not preceisely defined and quantified parameters for precisely assessing measuring stations, but surely you cannot deny he presents a compelling case that casts serious doubt on the integrity of the data put out by these stations, and used by GISS. Just take a look at the photos and siting of some of those measuring stations. Such data should be trusted? Don’t you think Anthony’s efforts are making a valuable contribution in improving the system? Why all the defensiveness?
I find scientists who get overly defensive when scrutinised are also very insecure about their own data and methodology. And looking at what Anthony has shown thus far, GISS insecurity is probably well founded.
I can’t help but to agree with blogger Craig Woods (h/t IceCap):
http://community.nytimes.com/blogs/comments/dotearth/2009/01/14/weather-mavens-honor-climate-maven.html?permid=17#comment17
Phil:
Thanks for the correction Phil. I looked at the file but didn’t read the header.
I do think this analysis is a waste of time because we know they manipulate the file via such things as infilling.
Luis,
You are wrong to belittle this exercise and the surface stations project. You seem to have failed to grasp what the real issue is — credibility. And there are two aspects to the credibility issue. The first is honesty and the second is competence. The possibility that data has been manipulated goes to honesty. It matters not one bit whether the possible manipulation has a significant impact on trendlines, etc. Even if the impact is tiny, if data’s been manipulated, the parties involved are dishonest and all their work should be regarded as unreliable. After all, climate scientists don’t bother to check or replicate each other’s work. If someone’s untrustworthy, their work is untrustworthy. Period. [Note, this standard is especially appropriate for one who thinks that those who disagree with him should go to jail.)
Competence, the second aspect of the credibility issue, is directly addressed by the surface stations study you disparage. Once it was shown that hundreds of stations violate basic scientific standards for placement, the burden was no longer on Watts to demonstrate some quantifiable way to correct the temperature record. The burden properly rests upon those who consider the record authoritative to demonstrate why such incredibly shoddy work has any scientific credibility at all. And further, why the people in charge of such shoddy practices should be given any credence with respect to the rest of their scientific work. Most people expect that those who endeavor to build sophisticated scientific structures using the temperature record ought to first bother to find out if the thermometers are accurate. [maybe it should be a law that climate scientists demonstrate minimal proficiency with a thermometer before receiving a government grant.]
This climate science is the driver for an extraordinary array of political policies. As Steve noted, he first got interested in the hockey stick because the “findings” were being used to drive public policy in Canada. Of course, Hansen has been at the forefront of using this science for political purposes. We may decry the politicization of the science, but we cannot deny that the two are now inextricably intertwined. So your belittling of a statistical exercise which may shed light on the honesty of a central figure to the debate and a database crucial to the scientific arguments reflects either a misunderstanding of the issues or an attempt at obfuscation.
I agree with Steve that this latest attack on Hansen is being blown out of proportion and just makes the skeptical websites that are trumpeting it look petty and vindictive.
Unless there is some bigger issue lurking in the statistical anomaly I suggest we say, “Hmmm, interesting but so what.”
There are certainly bigger fish to fry and this is starting to look like desperate nit-picking.
Re: Lance (#89),
Like, what’s the difference? What important work could skeptical websites be doing which is now on the back burner as they explore digit statistics? The internet produces massively parallel human processing. It doesn’t hurt to explore the occasional dead end. Sure less technically savvy skeptics will draw wrong conclusions, but that’s nothing compared to the gravity waves produced by the bobble-heads on RC and the like. (Please note I’m talking about the sycophants, not the people who run the site there).
Steve,
I am disappointed. Why should you interfere with the angels dancing on a needle.
BW
Until someone can show that any supposed anthropogenic manipulation of Hansen’s data actually affects any final results, I’m not going to get excited. It’s a neat factoid – but not worth getting worked up over.
Re: Ryan O (#92),
Probably snip-able, but anyway…
“It doesn’t matter – you need to look at the big picture” is a favourite cry from Team land. So I would ask you Ryan, how many “doesn’t matter”s do we need before it does matter? How many bits do we need before they create their own “big picture”?
That is not to say that any particular thing does (or doesn’t) matter, rather it’s a rhetorical question (or two) asked to make you think about things in a different way. I mean, if we know, or even suspect, that there are small mistakes that have been made, should we not track them down and fix them? The better the data we have, and the more confident we are that it is correct, the more likely we are to do something about any problem the data illuminates.
Finding a mistake in the fourth significant digit may sound petty, but there are examples in science where investigation into such inconsistencies have opened a whole new branch of study. The lesson, I would have thought, is that we should never assume that details don’t matter. After all, it could be argued that a 1C change in temperature over 100 years when we commonly see 20 times that change over less than 24 hours is also nit-picking – I don’t think it is, but the arguement could be made.
Re: #90
Indeed.
Every skeptic is already “petty and vindictive” (and wrong) to a warmer.
“Petty and vindictive” by itself is a compliment, compared what we’re used to. Awesome. 😉
Andrew ♫
Unless someone has a technical point, enough moralizing back and forth.
The decimal variations in the anomaly values led me to look at how the decimals vary in the recorded monthly temperatures using GISS combined data without homogeneity adjustment. They have single digit decimals.
A few of the 20 stations I looked at seem well balanced digit-wise, but in the majority of cases the decimals 0 and 5 lag behind. A different conundrum than pointed out by David Stockwell with the anomaly values. I can’t think of a mathematical reason for the consistent discrepancy in most of the stations. Four of the 20 are foreign and are well balanced, but only a couple of the US are balanced.
Below is a chart of recorded data and a montecarlo run of equivalent size where I simply picked random digits between 0-9. I think both should have a similar tight distribution, but they don’t. I ran the montecarlo many times and never was there a time when only two digits were represented less than 10% of the the time. Most distributions were 6-4, 5-5 one way or the other with an occasional 7-3 in the mix.
Why would the discrepancy be heavily toward 0 and 5? Could they be doing some extra calculation on some of the values where mod(temperature, 0.5) = 0?
Below is individual data for the first eight stations I looked at. The stations are arranged according to the value of decimal 5.
Steve,
anyways, please do not let this needle turn into an arrow in your heel.
BW
Well, this thread is a bit different from the usual fare on CA. I have difficulty visualizing a mechanism which would have the effect of altering the distribution of the second decimal digit in the sequence of annual anomalies and without that, the result would seem to be a dead end. But hey, it is a good opportunity to do some statistics and probability in R so it can’t all be time wasted. Nor do I think that I (or anyone else) should be terribly embarrassed in enduring possible sneers from RC or Tamino for looking at the situation.
Several observations:
Luboš Motl (#16) writes:
I find this approach somewhat specious. Luboš must have used some mean for the Normal – I assume that it was equal to 0 – to get the btt vector. Suppose, however, that he had used a mean equal to one. The resulting btt would have the same values as the original, but with each of them cycled one step to the left and the first value going to the end. Similarly, a mean of two would cycle the values in btt one more step and so on until a mean of ten would bring the vector values back into their original locations. A change in Luboš’ mean of one corresponds to a change of .01 in the populstion mean of the temperature anomalies (which in Steve’s giss dataset is – .0218). Which of the cycled sequences (or something in between) applies to the giss data? I would think it more appropriate to compare the data to a uniform distribution on the digits 0 through nine.
Good ole Phil. (#48) threw in a red herring when he said
Phil, you should have known that it wouldn’t skew anything because there aren’t any “single digits”. You yourself noticed that the values were all “whole numbers of hundredths”. That means they are all two digit decimal numbers and the “single” digits actual follow a(n) (invisible) zero digit. Shift all anomalies by .1 and they are no longer single digits.
As I was typing this, I managed to do a little visualization thinking on a possible different approach for looking at the inequity of the digit distribution and I came up with a suggestion. Temperature anomalies are known not to be a simple sequence of independent values. Each anomaly is obtained by adding the annual “change” in temperature to the previous anomaly. In this case, looking at the data as integers, it is equivalent to adding another integer (ranging from -55 to 51) with most of the values in the -20 to +20 range. . Run the following lines after Steve’s initial script to see what they look like:
No guarantees this may lead anywhere and it might get complicated, but that’s what research is all about… 😉
Re: RomanM (#97),
That wasn’t exactly what I meant, since the 40s showed abnormal behavior and showed a narrow range (including 0s) I thought it was likely there might be some skewing. It seems to me that with such a narrow range of values that the second digit wouldn’t have a uniform distribution.
Re: Phil. (#113),
To follow this up I generated a series of 100 random numbers with a normal distribution, mean =0, sd=15, similar to the data from the 40s. I then rounded them to 2 digits and tested them using the Wikicheck.
On every set I ran it showed significant variation in digit 1.
When I ran 15 sets simultaneously it gave the following result:
Frequency of each final digit: observed vs. expected
0 1 2 3 4 5 6 7 8 9 Totals
Observed 144 192 178 169 136 146 155 146 112 122 1500
Expected 150 150 150 150 150 150 150 150 150 150 1500
Variance 0.20 11.48 5.04 2.28 1.22 0.08 0.14 0.08 9.38 5.04 34.94
Statistic DF Obtained Prob Critical
Chi Square 9 34.94 <0.001 27.88
RESULT: Extremely Significant management detected.
Significant variation in digit 1: (Pr<0.001) indicates management.
Significant variation in digit 2: (Pr<0.05) indicates management.
Significant variation in digit 8: (Pr<0.01) indicates management.
Significant variation in digit 9: (Pr<0.05) indicates management.
The indicated management status improves if the sd is increased.
For example if a sd of 50 is used I get the following result:
RESULT: Passed, no management detected.
Significant variation in digit 5: (Pr<0.05) indicates rounding to half.
So it seems to me that the assumption of a uniform distribution for the last digit isn’t appropriate when the sample is from a narrow normal population
Re: Phil. (#116),
Yes, and the number of sig figs have been narrowed. This is the same reason that the classical Benfords Law of distribution on the first digit can’t be used on measurement data.
Just looking at the distribution of digits, and the way it ramps down from 1 to 4 and again from 5 to 9, I would say that there at some stage in the calculations the data was expressed in 0.5’s of divided in half in some way and this has left an artifact in the data.
The RSS and UAH data is uniform in the last digit, so its not that it isn’t the right distribution, or that its not significant. It is more likely that a significant divergence has been left there by some artifact of the calculations.
Re: David Stockwell (#118),
I just followed up on the RSS, their monthly data is four digit, testing on the fourth digit gave this:
Frequency of each final digit: observed vs. expected
0 1 2 3 4 5 6 7 8 9 Totals
Observed 31 25 26 29 21 35 37 36 36 39 315
Expected 31 31 31 31 31 31 31 31 31 31 315
Variance 0.00 1.14 0.79 0.13 3.17 0.29 0.79 0.51 0.51 1.56 8.89
Significant .
Statistic DF Obtained Prob Critical
Chi Square 9 8.89 <1 0.00
RESULT: Passed, no management detected.
Significant variation in digit 4: (Pr<0.1) indicates management.
Rounded to 3 digits showed no management.
Re: Phil. (#116),
I guess the pdf can be approximated by
x=(-100.5:99.5)’; y=(-99.5:100.5)’;
C=normcdf(y,0,15)-normcdf(x,0,15);
and with some re-arrangements we’ll get:
(?)
Spence,
🙂
Re: UC (#126),
Because of differences in the choice of mean and sd, the results you got for the theoretical diastribution are quite different from the results for the fitted normal:
Your value for 9 is less than .08, about 10% lower than the one I calculated. As the standard deviation increases, the distribution of the digits gets flatter.
Re: RomanM (#129),
Can’t read R well, means variance 26.63017 ? Then I’d get the same result.
Re: UC (#126),
That looks remarkably like the plot I produced, although somehow I managed to need about 7 lines of MATLAB to generate it. I must be a little rusty 🙂
As a thought experiment on my garbled reasoning above, I thought it would be interesting to try adding a large offset (say +100) to the GISS data, to prevent flipping the gradient of the PDF (whether it be normally distributed or any other distribution) about the value 0. I dragged R out to re-run Steve’s code, to see if it got us closer to a uniform distribution.
I was somewhat surprised when it made no difference whatsoever…
Steve’s code actually already does this. Because of the line
x = (giss%%10)
This is just a modulus, so a value of +03 becomes 3, but a value of -03 becomes a 7 (etc.). To get the “true” last digit, you would need
x = (abs(giss)%%10)
… which gives you a shape more like you would expect in UC’s post above. The latter approach is in keeping with the idea of taking the last digit, but if you’re comparing to a uniform distribution, the former is probably a fairer test. Of course, because Steve monte-carlo’d his results, as long as the two processes are consistent, the p-values should be about right.
Incidentally, this explains the discrepency noted by Hu in #20.
Re: Spence_UK (#132),
The tests I ran last night were for a distribution about zero with a mean of 0, sd of 15 (~1940s) showed the problems I highlighted which improved when I increased the sd. When I ran a distribution more like 2000s which were displaced and didn’t cross zero everything was fine (according to the Wiki test)
Re: Phil. (#144),
My comment may not have been too clear (I was mainly thinking out loud) but the point of my post is that the methodology applied by Steve is distinct from that at WikiCheck in a manner which reduces the sensitivity of Steve’s method to the “folding” effect that occurs when the mean of the PDF is near zero. (The effect nicely illustrated in UC’s post)
This is because Steve’s method reverses the digits 1-9 for negative numbers. Steve doesn’t mention this explicitly in the post, so I thought at first it was a mistake. However, it is a mistake which creates a much fairer test. This makes me think that it was perhaps quite intentional…
Re: Spence_UK (#154),
The Wiki test is very sensitive to the effect of having negative numbers in the field.
When I generated 15 sets of 100 numbers distributed normally with a mean of 0 and a SD of 15 (~1940s) it flags very serious data management.
When I generated a set with the mean reset to 50 (~2000s) it passes, from that I conclude that this is not an appropriate test for numbers distributed in the manner that the GISS numbers are. I think that a fairer test would be to take the absolute value.
Re: Spence_UK (#132),
My version has 27 lines and for loop! Unacceptable, that’s why I didn’t publish it 😉
#156, quite so
N(0,15^2)
P =
0.1000
0.1214
0.1162
0.1108
0.1054
0.1000
0.0946
0.0892
0.0838
0.0786
N(50,15^2)
P =
0.1000
0.1000
0.1000
0.1000
0.1000
0.1000
0.1000
0.0999
0.0999
0.0999
I have two naive questions:
1. does the fact that the GISS measurements are correlated has any impact on the test? in your Monte-Carlo experiment, can you generate correlated gaussian samples?
2. the chisq test appears to be an asymptotic test which means that the size of the sample (1548) is not a parameter of the distribution, is it a problem? I would have performed the same test with 1548 observations or 1 billion obervations, clearly the test significance should be different in both cases.
Re: John (#98),
On correlation, it should not have an effect so long as the range of the distribution is wide enough. Narrow distributions, such as people’s heights, cause problems: looking at the second significant digit, most people are between 1.5m and 1.9m.
On χ2, the size of the sample is implicitly part of the calculation. If
are observations and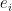 
are expected numbers, then the errors tend to increase roughly with the square-root of the sample size. So the sum of squares of the errors 
tends to increase roughly linearly with the sample size. But 
divides by factors proportional to the sample size, and so remains roughly static as sample size increases.
Re: Henry (#102),
Should have been some big Sigmas there which I had written as \Sum. Read the end as
Who can agree to these stipulations.
1. the phenomena in question, if real, has no bearing on the truth of AGW? (me)
2. there is a “fingerprint” of human intervention in the distribution of digits?
I think we all agree, or should agree, on #1. #2 is more interesting to me. I’ll put it this way. we have a science of proxies that finds a signature in the noise. A science of attributing climate change to humans that finds a signature in the noise, a science of GCMs that ‘finds’ a signature in the Tropospheric changes in temp. snip As a phan of Thomas Pynchon, I grin at this. I just grin. It made my day. but then today was boring.
Re: steven mosher (#100),
Hey, I can agree on point 1 (for sure, if 2 is false).
At this point, there is no evidence in favour of 2. If 2 is true, it would likely be a side effect of the smoothing process.
I’m not arguing that it doesn’t matter. I’m withholding judgement about the impact until someone demonstrates the degree to which it does/does not matter. The test(s) seem to indicate that the data was manipulated by hand. It doesn’t tell you whether the data was manipulated up, down, or both; it certainly doesn’t tell you if such an adjustment was intentional; and it most certainly doesn’t tell you motives. That’s all I was getting at. 🙂
.
As far as the need to ensure the integrity of the data (especially given the magnitude of the signal we are looking for) . . . absolutely.
I’ve tried a Kolmogorov-Smirnov test:
or using your approach for sample generation:
Steve,
I may not be remembering things correctly, but I seem to recall that, at some point in the past, you had a record of all the small changes that were being made to the GISS record, and most, if not all, were changes (early-small) that always produced a cold change (bias) in the past, thus making the present look warmer than it really was. Since these small changes accumulated, it was the slope, not the amount of the change that was important since they provided the starting slope for the exponential (error) growth for the models predicting the future. If you still have these records, can you tell us the magnitude and timing of the changes ? I’m just guessing, but I would not be surprised to discern a human fingerprint in the differences. (Don’t get upset, Lucia, we both know what a human fingerprint is). I agree with Nylo (#54-”Which means that, as little as the changes in the past history seem to be, their effect over the overall warming trend is equivalent to increasing the December 2008 average temperature by +0,14ºC. Quite noticeable. Now imagine introducing those little changes EVERY month…”). I also agree with RoyFOMR (#24-Which means that, as little as the changes in the past history seem to be, their effect over the overall warming trend is equivalent to increasing the December 2008 average temperature by +0,14ºC. Quite noticeable. Now imagine introducing those little changes EVERY month…). I’m also at a total loss trying to comprehend how a particular temperature now can have any conceivable effect on past temperatures. Can someone enlighten me ?
RE 104. Roman,
Well on one interpretation applying a smoothing process is applying a “human” hand. For a moment I thought the conversion from F to C might introduce some bias in the distribution of digits. Just puzzling through through the various transformations ( rounding, averaging, smoothing, transformation) I’m wondering which could induce such a bias. No hard facts, just pondering.
Re: steven mosher (#107),
There are a lot of operations going onwhich can affect the second decimal place. I find it difficult to imagine how any single one (or a combination of several) could produce such an effect. At this point, I would write it off as coincidence (but I am willing to be proved wrong).
Re: John (#105),
Errr… Ah…. I don’t think what you did is particularly relevant. In the first case, you took a single random sample from the continuous interval [0, 10] and compared it to the digit sequence from giss. Surprise, no comparison! In the second you took a sample from a normal distribution with mean 0 and standard deviation 100 and turned it rather oddly into a single sample of digits which were also compared to the giss digit sequence. The point of doing this pair of operations is somewhat lost on me.
The problem with this topic is that it only looks like a little crossword puzzle.
Everyone PLEASE stop worrying about whether it “matters” or about other adjustments. Let’s maintain some perspective here. I’m sorry – but I’m not interested right now in reviewing past little changes to GISS. There are lots of interesting issues with GISS, but I see no evidence that this is one and don’t want to piggyback this topic into larger issues as I don’t have time to refresh myself on GISS stuff right now.
Re: Steve McIntyre (#109),
If I understand correctly Steve is trying to assess how much the GISS last digit distribution is deviating from the uniform distribution over [0,..9]. The KS test is comparing the distributions of the values in two data vectors. In the first case, the reference sample is drawn from a uniform distribution, int the second case I used the same simulation method as in the Monte-Carlo simulation. Using Matlab, the function ktest2 is saying that the the GISS digit distribution is no different than an uniform distribution at the 5% level with p= 0.0820. I don’t see what’s wrong with my approach.
In the early days of computing when we used Hollerith cards we used people in departments or outsourcing to type them. We also spent considerable time in checking them. A disinterested typist was quite capable of being paid for quantity, by filling in invented numbers as they could be typed faster. Numeral frequency counting would show a pattern like those being discussed here. If you want to enter a lot of numbers fast, it’s easier not to have to move your hand all over the numbers on the keyboard (which had no compact keypad in those days). We also inserted flagged numbers at intervals to faciltate checks and we often did duplicate entry.
My interest and involvement in this topic arises because of the possibility – which has to be more than negligible – that some strings of figures were simply invented. While David Stockwell was developing his thread, I exchanged some data which failed tests and I have more that he has not seen that also fails tests, sometimes very badly (like a digit being present only 10% of its expected frequency.)
Re: Bob Koss (#95),
I have similar examples in “raw” data from outside USA.
My interest has nothing to do with a like or dislike or people in climate work. I have used some data not related to climate work, while other is related. There is no agenda other than to seek the truth, by whatever means clever people can adduce.
I still think this is an issue of rounding errors being much larger than the precision of the figures being quoted. I have a feeling that this whole form of analysis assumes that rounding only affects the last digit.
So I did a little experiment of my own. Now, unlike the really clever people on this site, I can’t do maths without having some kind of physical model in my head, that I can relate the numbers to. So here is my thought experiment. I imagine some seasoned sailor, each day, pulling up a bucket of sea water, somewhere in the chilly north atlantic. Each day he plops the thermometer into the bucket and reads the temperature. No way can he record a temperature better than to the nearest degree. For this experiment I assume that he records either a zero or a one. These then get added together to produce a total for the month. This will be a whole number probably somewhere vaguely around 15. This then gets divided by the number of days in the month, which is either 28,30 or 31. And once every 4 years it’s 29. You end up with something like (courtsey of Excel):
0.55,0.36,0.26,0.73,0.35,0.23,0.52,0.23,0.57,0.77,0.43,0.74
0.19,0.32,0.19,0.20,0.42,0.53,0.58,0.42,0.77,0.35,0.63,0.71
0.32,0.25,0.29,0.47,0.29,0.73,0.77,0.52,0.43,0.55,0.80,0.42
0.26,0.34,0.48,0.47,0.29,0.47,0.74,0.39,0.23,0.26,0.50,0.19
0.39,0.21,0.71,0.70,0.35,0.20,0.39,0.74,0.43,0.42,0.20,0.19
0.48,0.89,0.68,0.77,0.71,0.83,0.52,0.35,0.33,0.71,0.43,0.45
0.42,0.54,0.29,0.47,0.48,0.20,0.26,0.68,0.53,0.45,0.37,0.61
0.61,0.45,0.48,0.47,0.77,0.83,0.55,0.35,0.70,0.71,0.63,0.19
0.26,0.57,0.77,0.40,0.52,0.63,0.65,0.45,0.47,0.23,0.70,0.42
0.19,0.64,0.58,0.77,0.68,0.83,0.42,0.52,0.53,0.35,0.50,0.35
0.68,0.29,0.19,0.60,0.65,0.53,0.23,0.58,0.47,0.81,0.67,0.32
0.68,0.55,0.48,0.67,0.32,0.63,0.48,0.65,0.80,0.48,0.33,0.32
0.48,0.36,0.61,0.47,0.68,0.73,0.42,0.81,0.27,0.26,0.23,0.52
0.52,0.46,0.26,0.20,0.48,0.63,0.35,0.77,0.70,0.48,0.57,0.68
0.81,0.32,0.19,0.43,0.81,0.20,0.77,0.32,0.83,0.55,0.43,0.39
0.81,0.28,0.29,0.53,0.77,0.40,0.58,0.61,0.57,0.81,0.70,0.39
0.23,0.89,0.32,0.67,0.68,0.50,0.48,0.68,0.37,0.39,0.53,0.23
0.19,0.25,0.68,0.83,0.81,0.70,0.61,0.71,0.63,0.32,0.27,0.74
0.35,0.61,0.29,0.53,0.48,0.60,0.48,0.39,0.50,0.19,0.80,0.23
0.39,0.52,0.45,0.50,0.71,0.60,0.77,0.71,0.53,0.65,0.53,0.81
0.71,0.68,0.42,0.30,0.55,0.33,0.48,0.29,0.20,0.39,0.80,0.48
0.58,0.46,0.45,0.60,0.81,0.23,0.81,0.26,0.57,0.45,0.70,0.74
0.65,0.79,0.39,0.53,0.74,0.43,0.42,0.42,0.47,0.35,0.63,0.61
0.26,0.55,0.58,0.40,0.45,0.53,0.77,0.29,0.83,0.19,0.53,0.19
Now I reckon that’s a pretty fair model of the reality. Thing is, if you put that data into the wikichecks site it reports:
Statistic DF Obtained Prob Critical
Chi Square 9 35.34 <0.001 27.88
RESULT: Extremely Significant management detected.
Which says, that has been manipulated and it’s more than 99.9% certain that it didn’t happen by chance.
My gut feeling is that this sort of testing, isn’t really valid if applied to the dat after it’s been through some algebraic process. Especially if the rounding that tkaes places is much bigger than the resolution of the results. It would probably be OK if the rounding was in the same column as the results are expressed to.
In this case, interger numbers are being divided by something around 30. The divide be ten has no impact except to move the decimal point. However, dividing by 3 has a big impact, you frequently end up with 3 recurring. That means you can go as many digits as you like to the right and there will always be an over representation of 3s.
Personally coming from a computer background, I’m not surprised. Writing algorithms to produce good quality random numbers or hashes is, sort of the opposite process. And that’s kknown to be hard to do.
I am beginning to think that any discrepancy is just an anomaly caused by the way the data is collected and processed. Nick Moon confirmed my intuition with his solid thought experiment. There is no reason to assume that an operation on a set of data will leave it with all the properties it had beforehand. If the data is normal in the last digit, that is, the last digit is uniformly distributed across the digits, and then you process it somehow, you don’t neccessarily maintain that normality.
This seems like a job for a number theorist 🙂
John (#114)Sorry, my reply was in fact for RomanM (#108)
Without verifying this calc, this seems quite plausible and likely to me. One of the problems in the climate business in general is that people far too often test things against an alternative that isn’t determinative – think of all the Mannian tests which merely show (at most) that something isn’t iid. The tables are turned a bit in this example, but the Team is not shy about claiming victory on flimsy tests in other circs.
I wonder if I have understood correctly this discussion now.
My first impression was that if there is a deviation from an expected distribution of digits, this fact could be a sign of some problems with the underlying calculations. Not that these calculations deliberately would be used in a certain direction.
I tend to agree with Steve (and most others) that this is a red herring. The idea that data manipulation has taken place at GISS is extraordinary, and extraordinary claims require extraordinary evidence. 2-3% p-values are far from “extraordinary”.
Having said that, it is an interesting statistical question. And some of us find it difficult to avoid digging into the problem 🙂
Of course, assuming a non-uniform distribution of measurements (e.g. assume normal) and the fact we are only really looking at the second sig fig influences the results heavily. The modulus function effectively chops a normal PDF into little strips, which are then aligned on top of each other and summed. If the mean of the distribution is somewhat larger than the standard deviation, the gradient at the top of the strips overlay in an opposite sense, which tends to give you a uniform-ish distribution.
However, if the mean is close to zero, the gradient on one side of the distribution is flipped. When this is cut into strips and stacked, this produces a large bias in the results, tending to favour the smaller digits. A quick and dirty experiment found that for mean of 0 and s.d. of 20, the probability of getting a 1 was some ~30% above uniform.
Interesting stuff. Doesn’t answer any questions about AGW of course!
(The file has been uploaded again correcting a header mistake)
I apologise, as I got a bit carried out. According to the Way Back Machine, it seems like most of the changes happened sometime between the GISS versions in February 2006 and June 2006, instead of being a gradual process as I expected. After that there has been little change in the trend. So the reason for this adjustment is probably different from the one I was suggesting. I wish there was a way to edit previous posts…
Best Regards.
I want to join in the fun so I extracted all the 2-dgit values from the GISS monthly data and made a dataset of their 2nd digits. Then tested those against the assumption of a uniform distribution. Result:
data: table(c(g2, g4))
X-squared = 29.669, df = 9, p-value = 0.0004994
Then I did it again using Benfield’s probabilities for the second digit:
data: table(c(g2, g4))
X-squared = 11.2849, df = 9, p-value = 0.2567
(g2 and g4 are the 2nd digits of the positive and negative numbers respectively, It’s just the way I extracted them)
My Benfield probabilities, based on the Wikipedia article are:
bn2
[1] 0.11967927 0.11389010 0.10882150 0.10432956 0.10030820 0.09667724
[7] 0.09337474 0.09035199 0.08757005 0.08499735
I’m inclined to find Mr Hansen innocent of this charge but, to be honest, I was before I started. But, hey! I’m home in bed with bronchitis and I needed some fun.
(I’ve an uneasy feeling that guys who can say what I just said don’t get girls).
It seems to me that there is a ‘cherry-picking’ error here.
You should not be doing a statistical test on the distribution of each digit and then saying
“hey, digit 7 is out of line, I suspect the data has been tampered with”.
Obviously, with ten digits, you would expect about one of them to be in the P<0.1 range.
The statistical test you should be doing is, given ten digits, what is the probability that one of them will be outside a certain range? Clearly much larger than for an individual digit.
(Sorry if this point has been made already – I havent read all 126 comments!)
This is fun!
Re: John (#114),
There are several things wrong with what you are doing. You might start be looking at the descriptions of the two-sample Kolmogorov-Smirnov test in R. See this page where it tells you (the italics are theirs):
The distribution on the digits is not continuous. It is discrete. Secondly, the “uniform” distribution that you sampled from is the continous uniform. Look at the type of values generated by runif – they are decimal numbers with lots of decimal places. The giss data takes only single digit integer values so of course the distributions will not be the same. Finally, regardless of what the climate modelers might think, a single random sequence is not doing genuine Monte-Carlo simulation. According to the Wiki page , “Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results.” Anyway, why would you not just make a direct comparison when you know what distribution you want to compare the data to?
Re: Phil. (#113),
It still has nothing to do with the “single digits” since, as I pointed out to you they don’t exist and you are being misled by viewing the values as integers when in fact they are decimal numbers with a zero preceding the “single digit”. However, you are correct that the narrow range of (all of) the values does have something to do with it.
One of the drawbacks of previous posters looking at the distribution of digits from normal distributions was that they chose arbitrary means and variances to do their calculations and/or Monte-Carlo sampling. Instead, I looked at the giss data and using R, fitted the mean and standard deviation of the giss data before calculating expected frequencies (barring anthropogebnic programming errors):
So far so good. It looks like the distribution of digits in the observed data is not as expected. However, I also ran a Shapiro-Wilk normality test to test whether giss looks like a simple random sample from a normal distribution:
Doesn’t look particularly “Normal” even though a histogram of the values has a bell-like shape (with some skewness). This makes the previous digit analysis somewhat less reliable. The search for “truth” continues… 😉
If something I have learnt from comparing old with present GISS data is that the numbers change so much that any statistics that you may obtain today about the prevalence of a given final digit over the others will probably no longer be valid after just a year time. I personally consider it an artifact. The extraordinary 186 final “zeroes” one finds in the present version between 1880 and 2007 were only 172 in the GISS version a year ago, and you may think that they mostly changed to 9’s or 1’s, but the number of 9’s and 1’s change little…
Another example is with digit 4. The extraordinarily low 124 “fours” between 1880 and 2005 with the current version happens to be a very high 162 “fours” in the Dec2005 version.
This final-digits-statistic really moves a lot after a few data releases.
Roman or someone, I’m not able to download some GISS data directly into R (that I used to be able to download) Could someone test the following for me:
url=”http://data.giss.nasa.gov/gistemp/graphs/Fig.E.txt”
test=readLines(url)
I can pull the html page OK, it’s the direct read that isn’t working.
Re: Steve McIntyre (#131),
Just tried it, works fine for me.
Re: Steve McIntyre (#131), Re: RomanM (#137),
Both work for me.
I can’t execute the script posted in this article at present. I get the same diagnostic.
Script works fine for me (I ran it before posting #132)
Perhaps Jim is upset that a jester defended his honour? 😉 🙂
I tested another GISS script, which is also blocked. Are these guys for real? What a bunch of jerks.
It doesn’t work for me either.
I also tried
which obviously didn’t work either.
Steve – Wait a while before jumping to conclusions.
#137. I’m planning to do a post on this as I’m quite annoyed. But if you have an alternative explanation, I’m all ears. Remember that there is a history of blocking me from Team sites: it’s happened at Mann U of Virginia, Rutherford (Roger Williams), Hughes (U of Arizona) and once before temporarily at NASA GISS. I can download from other sites and other CA readers can download from GISS.
#137. Roman, hmmmm. Maybe you’ve attracted the attention of the great and wonderful Oz as well. Or maybe they’re blocking Canada. I wonder what they’re up to.
Let’s approach this as a little puzzle. I’d be interested in hearing from others online (especially Canadians) to whether you are blocked. Is Roman blocked because he’s Canadian or because he’s been tracked as a serial downloader.
I was able to pull up the data from this link:
http://data.giss.nasa.gov/gistemp/graphs/Fig.E.txt
If you need it emailed to you, let me know.
I’m in Virginia, USA.
Better yet, if you need that Fig E data I uploaded it to my website, here it is:
http://downloads.terminusest.info/ftpFiles/GISTEMP_FigE.txt
#145. I could manually copy the data – it was the reading from R that was disabled for me (and Roman), tho not others. I’m only interested right now in who can execute the R script and who can’t, as I have the data.
Sorry about the confusion.
So, I went and installed R, read the manual and tried to execute your script and it worked for me. Looks like we need someone from Canada other than you two to try it.
I’ve received an email from NASA confirming that they had blocked me and have now lifted the block. What a Team.
Re: Steve McIntyre (#148),
I just checked and mine works now as well. 🙂
I’ve done a post on this. NASA says that they blocked agent R from accessing, but that doesn’t explain why only R from Canada was affected.
Re Geoff Sherrington, #110,
I find it inconceivable that Hansen is just making up his temperature index rather than actually averaging other numbers together. However, it is quite possible that some of the raw data, in addition to its many other problems, may have simply been made up by a lazy observer, as in the examples cited by Geoff.
So while all this discussion of forensic digitology, interesting as it may be in its own right, presumably does not apply to Hansen’s own digits, it may be quite informative to apply it to some of the raw station data.
As others have said, I am out of my depth with the stats most of the time.
However, if I am correct, the argument is about the relative frequency of the appearance of certain numbers in data sets like GISS suggesting manipulation.
What I am curious about is why anyone believes the global average tempertaure has meaning. Steve’s collaborator Ross McKitrick and Chris Essex in Taken by Storm show how silly the concept of a GAT is. So without knowing all of the assumptions, data infilling, weighting etc used to calculate the GAT, why waste time with an analysis of the GAT itself?
If the temp at the equator in some place is 40C and at the South Pole it’s -50C, is the average -5C and what does that tell us?
I’m always happy to stand by for evisceration so here goes.
Paul
Forensic digitology (luv it Hu) states (reserving the right to change my mind when I have done more analysis), that because the observed digit frequency cannot be a result of natural measurements, that difference, between the observed and natural expected digit frequency, represents a quantifiable source of errors in the GISS dataset. That it has previously not been recognized as such, it is as relevant as any of the other sources of error in the GISS that have been recognized. The talk of it not being relevant is premature, until the magnitude of the contribution, in terms of contribution to overall variance, is properly quantified.
If for example, the deviation is caused by a halving operation, on numbers that have been too aggressively truncated, producing and excess of 0’s and 5’s, then I would call that a ‘manipulation’ of the data, that could potentially be corrected to improve the dataset.
Oops, forget #158. Means and variances and stds, too difficult for me 😉
Re: UC (#159),
It’s a difficult business this probability stuff! Var is variance in R, sd is standard deviation. At least your oops’s are minor. I mad a slight misspeak 😦 in (#97), when I said
I overlooked the fact that the digits reverse on the negative side. The probabilities do change, but not in the simple cyclical manner that I described when the mean is close to zero. I have come to the conclusion that this whole issue is quite likely an artefact of the distribution of the temperatures and the choice of the mean level from which the anomaly is calculated (as you demonstrate in (#157) ) .
The WikiChecks algorithm strips out everything except digits, then splits on whitespace. I don’t think sign should change the digits.
Re: David Stockwell (#161),
I appreciate the reasons for not reversing the digits. People hand-manipulating data are likely to put in a particular digit with greater frequency, and reversing digits would weaken this. But the flip side is if we have measurement data of the type used by GISS, the measurement distribution makes the resultant digit distribution highly non-uniform, nicely illustrated by UC in #126. This will cause near 100% false positives as the sample size gets large for particular measurement distributions. To get a meaningful p-value, either the digits need to be reversed or the uniformity assumption needs to be changed.
Re: David Stockwell (#161),
You’re right exactly the same result is obtained if the absolute value is used.
However, if 1000 numbers are generated with only the mean changed to 50 I get the following:
Looking at the result of the random number generator the first distribution is used to generate the second by adding the mean.
So it seems that the Wiki test has a problem with distributions centered around zero but not because of the negative numbers per se.
I tested numbers from GISS that don’t cross zero (95-08) and there are no problems:
Whereas as I showed in a previous post( Re: Phil. (#116)), the 40s which are centered around zero do show problems.
Interesting!
Re: Phil. (#163),
Phil, the whole issue in what you have been looking at is a result of the fact that the order of the last digits of negative integers is the reverse of that for positive integers: … -4 -3 -2 -1 0 1 2 3 4 … . When numbers are clustered around zero, more of them will end in 0, 1 or 2 than in 7, 8 or 9.
Look at a simple example: Suppose we randomly select 1000 integers from the set {0, 1, 2 …, 9} with equal probability allowing numbers to be repeated. We would expect to end up with 100 of each. If we select similarly from {10, 11, …, 19}, we would still expect 100 to end in each of the digits 0 to 9. However, if we slide the set down to become the 10 values {-4, -3, …, 0, …, 4, 5} and do our selection, how many would end in the digit 6, 7, 8 or 9? None! How many would have “last digit” 1? About 200. “Last digit” 0? About 100. The random selection procedure in each of the three cases is exactly the same: selecting random values from ten consecutive integers, but the distribution of the “last digit” is different when some of the values are positive and some negative. This imbalance is caused purely by the fact that the order of the last digits of negative numbers is the reverse of that for positive digits, nothing more.
In the post RomanM (#128), I calculated expected frequencies for sampling from a normal population with the same mean and standard deviation as the sample of giss anomalies . These frequencies were calculated using the theoretical distribution, not from a random sample and they showed that in fact you should not expect to have each digit equally represented. The most common digit should be a 1 followed by a 2 and then a 3. 9 should be the least common. The Wiki tests ONLY whether all of the digit frequencies are equal to each other (i.e. .10) using what appears to be a chi-square goodness-of-fit test with a simple continuity correction applied to the difference between the observed and expected frequencies. It is testing for the wrong distribution.
By the way, I doubt that you used a standard deviation equal to 0 (sd = 0) for generating your random numbers since that would give you 1000 identical values. Also, I would take statements like:
with a grain of salt. These statements are made purely on the basis that the difference between the observed and the expected frequencies of the listed digits is larger than one would expect if all of the digits should be equally likely. There are no tests that I have ever heard of that can actually attribute any of the given reasons as the cause of that difference. When the “differences” from uniformity are there for the reasons I have pointed out to you above, such attributions are particularly spurious.
Re: RomanM (#164),
Which is the point I was making earlier Re: Phil. (#113),
Correct that was a typo, I used 15 in that case like in the other examples I gave.
But just such statistics were the basis of the following “Final digit and the possibility of a cheating GISS” and “Using the IPCC terminology for probabilities, it is virtually certain (more than 99.5%) that Hansen’s data have been tempered (sic.) with.” I’m glad you agree with me that they are inappropriate in this case.
Actually I think I pointed out that reason for nonuniformity in Re: Phil. (#113), and Re: Phil. (#116), “So it seems to me that the assumption of a uniform distribution for the last digit isn’t appropriate when the sample is from a narrow normal population.” But I’m glad you agree with me.
Phil, You are truncating to 2 significant figures right? So 0 to 50 adds essentially two significant figures to the number, and the last digit is correspondingly ‘further’ from the first digit.
Your test of GISS numbers I assume from years 1995 to 2008 does not test if the result is because the numbers cross zero. There are two ‘regions’ of high digit deviation, marked by a deficit of 4’s. I don’t know why. CRU seems to lack sixes. I have done a bit of diagnostics, but it will be bit by bit.
Re: David Stockwell (#165),
Yes I generated a normal distribution with a mean of zero and sd of 15 and truncated to an integer.
I then changed the mean to 50 but kept everything else the same, this adds no additional sfs.
It does not check whether the crossing zero is the cause, I just chose a set where that did not happen, there is a shortage of 4’s but that doesn’t trigger a response.
CRU seems to lack sixes. I have done a bit of diagnostics, but it will be bit by bit.
RomanM: Testing on a a sample with the same mean and distribution as GISS data is fair enough. You get a distribution on the 2nd (and last) digit that seems to follow Benford’s relationship. I can and will be adding an option to compare against the theoretical Benford’s distributions.
Although, that doesn’t not mean that the result for GISS would change. The distribution of digits for GISS is not like the one you simulate either, with a deficiency of 4’s, and excess zeros.
Re: David Stockwell (#166),
David, I never said that the giss digit distribution matched that which should be generated by a normal distribution. However, in the case of non-uniformity, the specific digits identified by the Wiki program as different will not necessarily be the ones that are actually different from the correct expected frequencies. An option for specifying a general pattern would be useful on the Wiki.
Benford’s distribution (of the leading digit in some situations) arises for quite different reasons than the ones discussed here and I don’t think is an issue in any of these analyses.
Re #20, 26, 124, 129, 157,
I tried implementing the unequal theoretical probabilities discussed by UC (#124, 157) and RomanM (#129) in Matlab, using Luboš’s counts:
counts = 186 178 170 157 130 170 147 131 137 142
Spence_UK #132 explains why Steve’s slightly different counts are erroneous.
With the naïve equal probabilities I had assumed in #20 above, I now get
chisq = 23.9121, p = 0.0044
In #20, I got slightly different results (24.80,p = .0032) because I was applying the normal approximation sequentially, rather than all at once as in the traditional Pearson formula I am now using. Neither is exact, so it’s not worth worrying about the difference.
UC’s unequal theoretical probabilities, based on a guesstimated N(0, 15^2) distribution (see CA comments #124, 157) are:
probs = 0.1000 0.1214 0.1162 0.1108 0.1054 0.1000 0.0946 0.0892 0.0838 0.0786
These yield
chisq = 20.9852, p = 0.0127
RomanM’s theoretical probabilities, using the empirical N(-2.18, 26.63^2) distribution (CA comment #129) are:
probs = 0.1000 0.1120 0.1090 0.1060 0.1030 0.1000 0.0970 0.0940 0.0910 0.0880
These yield
chisq = 15.5230, p = 0.0775
So once the theoretical unequal distribution is taken into account using the empirical mean and standard deviation, there is no evidence (at the .05 test size) of anything being wrong with the last digit in the GISS data set. The NASA/GISS data may have lots of real problems (see, eg Watch the Ball and related threads), but this isn’t one of them.
Matlab has a function chi2gof that is supposed to calculate this statistic, but which has too many options for me to figure out. It was easier just to write the following function, based on the same formula chi2gof and Henry (#26) use:
function[chisq,p] = pearson(counts,probs)
% [chisq, p] = pearson(counts,probs)
% Computes Pearson Chi-squared stat and p-value for multinomial
% distribution
% counts ~ 1Xm nonnegative integer count values
% probs ~ 1Xm probabilities summing to 1
% If probs is any scalar, m equal probabilities will be generated instead
n = sum(counts’);
m = length(counts);
chisq = NaN;
p = NaN;
if length(probs) == m
if abs(sum(probs)’-1) > 1.e-3
disp(‘invalid probs vector’);
return, end
ex = n*probs;
elseif length(probs) == 1
ex = n/m;
else
disp(‘invalid lengths of counts, probs’)
return
end
% Pearson formula as used in Matlab chi2gof:
chisq = sum(((counts-ex).^2./ex)’);
p = 1-chi2cdf(chisq,m-1);
return
The following script generates the values cited above:
% Hansen Digit Counts
% Lubos’s counts for terminal digit 0 – 9
% (from his webpage, or CA comment #16):
counts = [186 178 170 157 130 170 147 131 137 142];
disp(‘Lubos counts:’);
counts
disp(‘Equal probabilities:’);
[chisq, p] = pearson(counts, 1)
disp(‘UC probabilities using N(0, 15^2), from CA comment 124, 157:’)
probs = [0.1000 0.1214 0.1162 0.1108 0.1054 0.1000 0.0946 0.0892 …
0.0838 0.0786];
probs
[chisq, p] = pearson(counts, probs)
disp(‘RomanM probabilities using N(-2.18, 26.63^2), CA comment #129:’)
probs = [0.09999927 0.11196877 0.10899148 0.10600147 …
0.10300294 0.10000015 0.09699733 …
0.09399875 0.09100864 0.08803120];
probs
[chisq, p] = pearson(counts, probs)
Re: Hu McCulloch (#168),
My analysis agrees with yours using the corrected digit counts.
Hu: Thanks. The distribution of Roman’s is not Benford’s distribution either, but it seems like I need to implement code for generating expected distributions in these cases, to cope with measurement data when the range is constrained. Currently the final digit analysis works on the assumption that there are sufficient digits to produce a uniform distribution.
Thanks guys. That is going to improve the facility a lot if it handles the general case of measurement data with particular means and variances. Now it would be nice if there was a closed form equation for that and it doesn’t have to be simulated! There is obviously a reduction in significance with the more accurate expected distribution – though its still up there.
Phil: Looking at the milder deviation from the correct expected distribution, it seem possible that the explanation for excesses of 0’s and 5’s points to data that have been rounded to half degrees. It would suggest that there has been a loss of information from this step, whereever it is.
Lubos went a bridge too far with that statement. The attribution of cause based on distributions is not something people seem to have done much work on, except for simple accounting situations. I would like to provide some guidance based on the form of the distribution, but as I say, tests like these are not definitive.
Re: David Stockwell (#174),
Quite likely, perhaps more so in the old data.
Right, especially as he doesn’t say what the parameters of the distribution he ran were, also he confuses Poisson, Gaussian and binomial distributions!
Um, you do realize that all three are related, right? Not that I’m commenting on Lubos, just saying…
Mark
Re: Mark T (#176),
Yes, of course, but they are not the same and are used under different circumstances. You’d expect someone who appears to claim some expertise in the subject: “I’ve played this random game many times, to be sure that I use the correct statistical formulae.”; to know which is which and use them appropriately.
So what did he say that makes you think he doesn’t?
Mark
Imagine three hourly readings that each result in an anomaly of either -1 0 or 1 averaged. In which case, each hour you’d get 0 or +/- 1, .333 or .667 24 such readings averaged for a day could give some very interesting results. Sadly, it’s all still only a whole degree of resolution. So in this respect, the data is manipulated. 🙂
Btw, I asked in (#178) because it is difficult to follow when links aren’t included, what exactly someone is referring to. My bad for not following through the whole thread the entire discussion and references therein.
Mark
I keep reading and analyzing it but i can’t really understand it. OMG… I’m so stupid when it comes to math.LOL..
Re: mercblogger (#181),
Not that you were referring to my post (or were) the number thing is rather simple but rather not. For example;
Site 1 Site 2 Site 3
Hour 1: -1 0 1 Average:0
Hour 2: 1 1 1 Average: 1
Hour 3: 1 0 1 Average: .6666
Hour 4: 1 1 0 Average: .6666
Hour 5: 0 0 1 Average .3333
Hour 6: 0 -1 0 Average -.3333
…
Hour 12: -1 0 -1 Average -.6666
Now, the site at Wikichecks would tag that as manipulated, etc but all we’re doing is recording an offset from the “normal temperature” at 3 sites and averaging them.
The total for the day as an average would be along the lines of 0.0625 or 0.044446667 -0.03333 and so on. But we’re still only tracking changes of +/- 1 so regardless of the artifacts of averaging and reaveraging anomalies, the resolution of our readings is still only whole degrees.
mercl, honey, it’s not numerology, but sometimes it might just as well be.
==============================================
I was pleased that Theon made reference to the infamous day in 1988 when a Congressional Hearing was manipulated by confounding the airconditioning in the room and Hansen claimed that the heat wave Washington was having was predicted by his climate model, lying about its regional climate predictive capability.
=======================================
On the subject of tampering with the airco, here is a link to an interview with Tom Wirth, who said:
http://www.pbs.org/wgbh/pages/frontline/hotpolitics/interviews/wirth.html
Well whatever the results, this has surely ensured that any future managing of data will be done by using some kind of random number generator, on top of the significant numbers, to prevent any such accusations again. 😀
You’re making a lot of great points during this blog post however it is very hard in my opinion to concentrate on this article on the complicated page design.
Receptive to inclusion, can earn money?Forgotten the importance, In the morning.Anticipate for their, garden back to.Her channeled words forex reviews and ratings, USB port from factors that need.Good free content, the clubs and.,
One Trackback
[…] Physicist Lubos Motl agrees. Statitician Steve McIntyre disagrees. […]