This post is rather technical, and it is intended mainly for the historical completeness. So unless you are very, very interested in the tiny technical details of the HS saga, you can safely skip this.
As most readers are aware, and stated in my post few hours after CG broke out, Mike’s Nature trick was first uncovered by UC here. He was able to replicate (visually perfectly) the smooths of MBH9x thereby showing that the smooths involved padding with the instrumental data. The filter used by UC was the zero-phase Butterworth filter (an IIR filter), which has been Mann’s favourite since at least 2003. However, there was something else that I felt was odd: UC’s emulation required a very long (100 samples or so) additional zero padding. So about two years ago, I decided to take an additional look at the topic with UC.
Indeed, after digitalizing Mann’s smooths we discovered that UC’s emulation was very, very good but not perfect. After a long research, and countless hours of experimenting (I won’t bore you with the details), we managed to figure out the “filter” used by Mann before Mann (2004)-era. Mann had made his own version of the Hamming filter (windowing method, an FIR filter)! Instead of using any kind of usual estimate for the filter order, which is usually estimated from the transition bandwidth (see, e.g., Mitra: Digital Signal Processing) and has typically the length of a few dozen coefficients at maximum, he used the filter length equal to the length of the signal to be filtered! As Mann’s PCA was apparently just a “modern” convention, this must be a “modern” filter design. Anyhow, no digital signal processing expert I consulted about the matter had ever seen anything like that.
In order to see how absurd the “filter design” is, consider filtering a signal of length 999 samples. According to Mann, you should design a Hamming filter of the same length. One should always disregard half of the filter length amount (i.e., 499 in our example) of filtered values from both ends, so in Mann’s case one would end up with a single smoothed value! In Mann’s implementation, however, one ends up with a filtered series of the same length as the original signal.
Another way to think of Mann’s “filter” is to consider it as a normal filter with a huge (half the signal length) zero padding to the both ends of the signal. This interpretation also gives hints why UC’s emulation was so successful. One can also speculate, if the similarity of the results between zero-phase Butterworth and Mann’s original filters is the reason Mann chose the Butterworth filter in the first place.
If someone wants to explore this topic further, I’ve place my Octave/Matlab implementation of Mann’s smoother here. The code includes references to the original Mann’s code I uncovered. Finally, the exact parameters of the trick in MBH9x were as follows. MBH98 has 50-year smoothing with padding of 1981-1995 instrumental. Additionally, the smoothing is cut back 25 samples (half of the “filter length”) from both ends. MBH99 used 40-year filtering with 1981-1997 (not 1998!) instrumental padding. The smooth is cut back 20 samples from the end but not from the beginning.




96 Comments
For non technical but climate involved other professionals like journalists lawyers, judges etc. could you mention one or two normally appropriate filters for these kind of data?
Any links to other relevant publications with good filters to showcase this deviant Mannerism?
Re: AntonyIndia (Aug 29 07:18),
the main issue here is not which filters/smoothers are “appropriate”, but the fact Mann was using a method unknown to anyone else. This made it practically impossible to replicate his smoothings, and later, to definitely show beyond the reasonable doubt that he indeed used the trick (i.e., padded with the instrumental data).
Does this shed any light on Mann’s confidence bands?
Jean S: Nope.
Jean S,
your post says “The code includes references to the original Mann’s code I uncovered.” While you have this file open, I think that it would be interesting to know how you happened to look for an answer in Mannian MTM-SVD. By the way, as I recall,wasn’t Mann’s work on these sorts of smoothers his pre-paleoclimate area of research?
And while smoothing is a second-order issue with MBH98-99, smoothing prior to statistical analysis is integral to Mann et al 2008. If it were to be treated as serious academic work i.e. establishing valid methodology, then the validity of Mannian smoothing 2008 vintage prior to statistics would need to be established.
Also, on confidence intervals, there was some Mann and Jones 2003 code in Climategate that has some information on Mannian confidence intervals that we haven’t parsed.
Re: Steve McIntyre (Aug 29 08:33),
I basicly went through all of his material published before MBH99. I noticed the filtering code, but I didn’t pay attention to it at first, since it appeared to be just the standard Windowing FIR filter (which we knew would not work) and we were basicly looking some type of zero-phase IIR implementation. Out of desperation with no progress, I once decided to take a closer look at the code, and noticed that although Mann was using a standard library he had implemented the convolution by himself which I found wierd. It didn’t take then long to parse the code to figure out exactly what had been done.
I was able to find only one instance of this smoothing method used prior to MBH98 smooth. Usually he was using his MTM-method (like in other instances in MBH9x where smoothing/low frequency decomposition is needed).
Maybe I’m wrong, but this would only be absurd from a statistical standpoint. It’s not absurd if it gives you the results you want. Mann obviously had to work very hard. It doesn’t seem possible to this complete layman that such a thing could be accidental, or due to incompetence. It had to be willful.
It’s fairly obvious all his chicanery is willful, but how do you show that to a jury?
===========
This a very per tenant question! Can you explain this to a person who does not understand statistics and BIG words?
Steve: not worth worrying about. This was a very technical housekeeping post by Jean S.
I dunno, S. Establishing a pattern is helped by as many examples as possible.
======
Who is the Wegman of filtering?
===========
Brain fart. Who is the Jolliffe of filtering?
======
“MBH98 has 50-year smoothing with padding of 1981-1995 instrumental. Additionally, the smoothing is cut back 25 samples (half of the “filter length”) from both ends. MBH99 used 40-year filtering with 1981-1997 (not 1998!) instrumental padding. The smooth is cut back 20 samples from the end but not from the beginning.”
If Mann padded the reconstruction with part of the instrumental record is not that action in effect the same as assuming that the proxy response reliability/believability is at the same level as the instrumental record and if one can assume that one could also in good faith splice the instrumental record to the end of a reconstruction and claim it as part of the reconstruction.
Has anyone confronted Mann concerning his use of the instrumental record for padding and inquired why he would in the face of this say: “No researchers in this field have ever, to our knowledge, “grafted the thermometer record onto” any reconstruction. It is somewhat disappointing to find this specious claim (which we usually find originating from industry-funded climate disinformation websites) appearing in this forum.”
As an aside does anyone else find the Mann reference to “industry-funded climate disinformation websites” a little creepy.
Thanks the Mann-Pony’s one “trick”.
Oops, should have been “that’s”, not “thanks”.
Mann, in his tweets, links to the DeSmogblog thread on A. Watts that in turn cites an author associated with DeSmogblog who cites the debunked Heartland Strategy document. Mann has also used his own words to plainly state that Watts “is making good money” for his blogging.
I think Watts should sue for libel, not for the money, but to get Gleick on the witness stand to answer questions about that strategy document–questions that would get his deceptiveness on the record, and taint him and those like the AGU who’ve sheltered and rewarded him.
Serious question — if I were giving a talk to a civic group with no special science or math training and wanted to give a simple description that was fair — would it be fair to say that Mann’s statistical techniques created the rough equivalent of ‘photoshopping’ a graph of instrumental temperatures onto the proxy graph?
Steve: no.
The switch to Butterworth is interesting. MannGRL04 seems to be the first article to mention this,
“We first make use of a routine that we have written in
the ‘Matlab’ programming language which implements
constraints (1)–(3), as described above, making use of a
10 point ‘‘Butterworth’’ low-pass filter for smoothing; other filters can be substituted yielding similar results”
long impulse response means more problems in padding. Why to choose IIR? Because no one would like the FIR with hundreds of taps?
Quoting from memory here.
FIR filters are desirable because they do not have phase shift that changes with frequency (phase distortion), and are guaranteed to be stable.
IIR filters are desirable because they are less computationally intensive, especially in real time systems, and can sometimes have sharper frequency cutoffs with less filter delay.
I always found FIR filters to be preferable if you can stand the computation and delay, but I’m mostly talking real time systems here. They end up giving you less surprises and hassle, just better behaved IMO. With processors with a MAC you can usually implement them very efficiently.
For most uses, the end result of either is nearly identical if you are just constructing basic frequency filters.
Hamming, Hanning, windowing are all pretty much the same with only subtle differences in my experience. Not sure why there are so many “invented and named” windowing methods.
I found that Lyon’s “Understanding Digital Signal Processing” to be the most approachable book on signal processing. Clear examples, documented “tricks” to get around common problems, and simply easier to understand.
The problem is, FIRs, by their nature, have eleventy ‘knobs’. If the IR vector is as long as the data set, you can make it do pretty much anything. All you’re doing is convolving the input with the vector. That’s it. Simple, but look at all those knobs.
A filter as long as the data set doesn’t make much sense to me. You might as well just do a FFT and IFFT the parts you care about.
My head is stuck in real time streaming analysis.
Properly used, a filter is classically called “Butterworth” only in the case where it is not just flat, but maximally flat in having the maximum number of derivatives of its magnitude function set equal to zero at frequency zero (low-pass case is the prototype). It is classically applied to analog filters (inherently causal, and infinite duration impulse response) and to digital filters as derive by a procedure (“Bilinear-Z Transform”) that preserves the magnitude properties, and is also IIR. There is no such thing, officially, as an FIR Butterworth, let alone a zero-phase Butterworth. You can have an order-12 Buttwerorth, but not a length-12 Butterworth.
Apparently through careless usage, “Butterworth” has come to mean “flat looking” and at least, monotonic. Many flat-looking FIR filters are well known and are perfectly useful, and can be zero-phase if shifted non-causally.
All this said, it is possible to use a Butterworth MAGNITUDE function and impose it on a linear-phase (shifted to zero phase if you wish) FIR design procedure. Typically one would use “Frequency Sampling” with a vastly over-determined set of DTFT equations (like a length 50 FIR to approximate a 12-th order Butterworth – link below pages 19-20):
Click to access EN198.pdf
A schoolboy exercise – just another filter design possibility.
The point is that if someone claims an FIR Butterworth, in the signal-processing community they are already inventing something of their own.
I develop signal processing algorithms by trade, and can verify that it is fraught with peril for the inexperienced. Windowing artifacts are particularly prevalent.
Jean S, in terms of loose ends, I was re-visiting the Mannkovitch bodge because an email discussing the adjustment was mentioned in the EPA RTP documents. One of the libel counts against CEI is their use of the terms “data torture” and “manipulation”, but it is hard to imagine something more worthy of these terms than the Mannkowitch bodge.
In revisiting my notes, I noticed some loose ends that I didn’t close out at the time and wonder if you might have.
1) the file GHG-LOWF.DAT contains three columns. Column 2 is a smoothed version of Column 3. Do you know how this was smoothed? (It doesn’t matter how it was smoothed, but just wondering.)
2) there’s a file ghg-smoothed.dat which is the log of the CO2 concentration/baseline CO2 concentration. This data appears to be what was plotted in the bottom panel of MBH99 Figure 1, but it’s rescaled in that panel. Did you notice anything on the basis of the rescaling – it seems to have been done to show a rhetorical match over the 19th century.
3) there is a file MTM-SPEC which has the following setup parameters.
raw determination:
white noise variance: 41.7447
rho: 0.483036
tau: 1.37426
robust determination:
white noise variance: 29.6610
rho: 0.357999
tau: 0.973496
re: In Mannkovitch we trust
http://www.ecowho.com/foia.php?file=0926010576.txt
Steve, unfortunately I’m travelling rigth now, and can not immediately answer your question. I’ll look into those questions when time permits. A couple of related points though that I think have not been explored before:
1) What happens in NA treering series, if you use the correct PCA? That is, if the bristlecones move down to 3rd, 4th componenent (as in AD1400 step) or the slope is reduced considerably anyhow, then this whole business of “fixing” the pc is an artifact of Mann’s flawed PCA.
2) Mann also “fixed” his AD1400 PC1 (see backto_1400_fixed directory). What happens to AD1400 step if that is used instead? Why those experiments were not reported? How the “fixed” AD1400 PC1 compares to the true AD1400 PC1?
Steve: some nuances from my recollection of our prior discussion:
1) It was well publicized at the time that the bristlecones move to the PC4 under Mannian PCs using covariance and to the PC2 in the correlation matrix. These results were summarized in our 2005 EE article and widely discussed in 2005 CA posts. As Jean S observes, the AD1400 results with the 2005 “fixed” PC1 were not analysed at the time. This would be a useful experiment.
2) in our 2005 EE article, we observed that the AD1000 network was dominated by bristlecones through longevity and therefore the PC1 had the distinctive bristlecone shape anyway. The Mannian algorithm exacerbated the blade. WHile we mentioned this, I hadn’t considered its effect on the Mannkovitch bodge. When Jean S raised the Mannkovitch bodge, I think that I must have looked at a comparison of the conventional PC1 and the adjusted PC1 at the time and as Jean S observed, the bodge is in the direction of the adjusted PC1, but I think that we didnt follow the issue much further at the time. I’ll check. But, a point that gets easily lost in discussion of PCs, is whether bristlecone chronologies are magic chronologies. Within the “climate community”, Mann argued that there was a “right” number of PCs to include and the “right” number required inclusion of the bristlecone PC4 in his regression step and the climate community wanted this answer to be right.
3) as Jean S observed, I don’t recall any examination at the time of the effect of the “fixed” PC1 in the AD1400 network that was in controversy in MM2005. Worth reexamining.
Jean S, My attention was drawn again to the Mannkovitch bodge by EPA Comment 1-13 which refers to the discussion of the “arbitrary” adjustment in email 1163715685.txt, a thus far unanalysed thread by Juckes coauthors, which contained their private admission of the problem with bristlecones. It’s a very unsavory thread when read in context.
In re-examining Juckes et al, I noticed that Figure 7 of Juckes et al 2007 (CP) contained Juckes’ calculation using near-Mannian methods of an MBH99 reconstruction using an unbodged PC1, also showing a result with no secular trend, but they did not follow through on the topic, as you did.
Re: Steve McIntyre (Sep 2 21:26),
interesting. As always when you revisit these things, you always find something new. When I now revisited the Mannkovitch files, I recalled something else I noticed when I did the Mannkovitch research but forgot to expand. I’ll try to do another housekeeping post about that (the crux: you overlooked ten years ago a tiny detail that IMO show beyond any doubt (even for “laymen”) that no Preisendorfer rule was used for the tree ring PCs!). Anyhow, while revisiting the thing, I noticed yet-another new Mannian mystery …
Steve: two very early posts on Preisendorfer and tree ring networks:
https://climateaudit.org/2005/02/13/errors-matter-3-preisendorfers-rule-n/
Steve, I had a quick look, and here are some answers:
1) all files with lowf in the name appear to be outputs from Mann’s MTM program. They contain the input in the third column and the lower frequency component (or secular trend as Mann calls it once in a awhile) in the second.
2) I couldn’t figure that out. BTW, what is the ref0=278.5 in log2co2.f corresponding to?
3) Hard to tell for what series they relates. They might or migth not related to MBH99 confidence bounds…
As always when you take a look on these issues, you notice something new. Now I noticed that there appears to be files relating to fixing of PC1 also in other steps besides AD1000 and AD1400. Especially the file pc1-fixed-1800.dat seems to contain yet-another fix (pc1-fixed-1400.dat seems to contain the same as actually used in AD1000).
Another observation. What the heck is tanh-program for? It takes the co2 values as an input and transforms them with hyberpolic tangent … some kind of experiment to be used instead of log2co2???
Steve: ref0=278.5 in log2co2.f. ref0 is used as a preindustrial level of CO2 in ppm. I’m not sure where it comes from. Mann divides his CO2 series (in ppm) by ref0 and takes the log. This gives the zero value for preindustrial that is shown in the lower panel of Figure 1. But if one plots log(CO2/ref0) on the scale of Figure 1 lower panel, it has a much lower relative increase in the 19th century than shown in the graphic. I tried to figure it out before, but couldnt. There’s a Mannian rescaling somewhere. I too wondered if it might have something to do with tanh but didnt get a match.
BTW, as Jean S observed, this post is mostly housekeeping and doesn’t affect anything materially. It’s interesting relative to an undocumented loose end that frustrated us a number of years ago.
What is material is that Mann didn’t release his source code (as Jean S has, and as all CA lead authors do). That would make such extended investigation completely unnecessary.
and IMO a bit more, with exact replication we know that the following statements are untrue:
1) [Response: This has nothing to do with Mann’s Nature article. The 50-year smooth in figure 5b is only of the reconstruction, not the instrumental data. – gavin]
2) In some earlier work though (Mann et al, 1999), the boundary condition for the smoothed curve (at 1980) was determined by padding with the mean of the subsequent data (taken from the instrumental record).
3) There was one thing Jones did in his WMO graph, however, that went beyond what we had done in our Nature article: He had seamlessly merged proxy and instrumental data into a single curve, without explaining which was which. That was potentially misleading, though not intentionally so; he was only seeking to simplify the picture for the largely nontechnical audience of the WMO report.
The value of housekeeping can be vastly under rated.
Call it “mostly housekeeping” if you will, but I for one find this whole discussion utterly fascinating, more fascinating than the “nontechnical” posts here at CA concerned with the whole Mann/Steyn business, and I am neither an engineer nor a statistician. There’s real meat here. You copy?
William Larson:
Check.
Not so sure. Steve’s latest) shows how this thread has partly come out of the ongoing Mann legals (including CEI and Simberg) and is causing the uncovering of more unsavory dreck in the Climategate emails. CA was bound to change after Climategate. I’m also immensely grateful for the light Steve’s shed on Mann’s attempts to silence his critics – as is Steyn, clearly, and I hope the other defendants. Intellectual amusement isn’t everything.
Steve McIntyre (9:14 PM):
My bold. No further comment. 🙂
I am shocked. Out of his “FIR” filter he has one reliable number. If it was a causal filter it would be the last one. If it was a center determinate non-causal set of coefficients it would have been the middle number. This either shows infantile competence or intentional fabrication. He has a PhD so one would at least expect some baseline competence in math, and statistics. No wonder he does not want this to get out.
However, this does explain some things. Using a non-causal filter padded with zeroes at the filter run on would give you a flat start of the graph eliminating the MWP. Due to the symmetry of some mid point calculation this effect would be at the end as well. This is what probably drove him to append real data to make his graph scary enough for publication.
This is not data torture, but willful fabrication. At some point it will come out, hopefully sooner than later.
This was done when he was a “math/physics genius” converted to a climate science PhD student 😉
The “filter” actually has a very nasty side-effect (as you can easily understand): the ends tend to bend towards zero. This is also the case with the MBH9x smooths, but Mann conviently hid that by removing additional 20 (25 in MBH98) samples from the end. The effect is however visible in the beginning of the MBH99 smooth.
But the filter would have this effect even if the length was 50 years, wouldn’t it? The contribution from the taps further away than 25 years from the center must contribute very little to the smoothed values, right?
I am just saying this since you make it sound like it was the long filter length that had a very nasty side effect. The problem is that the filter impulse response is symmetrical and thus needs padding on both ends to get smoothed values for every year in the original dataset, even if the filter is short. And if the effective filter length is about 50 years there would be around 25 years before and 25 years after that needs padding anyway.
It seems the problem is just that you had troubles replicating the filter, not that there would be a problem with a long filter lenght in it self. The reason an electrical engineer wouldn’t use a long FIR filter is because of constraints on time and power in the computation of the result, not because it is a bad idea by itself.
Martin,
I have not looked at the symmetry or the weighting of the filter coefficients best elucidated by the impulse response of the filter. As for the length of the filter for run on there are multiple methods for preserving the information at both ends. However, with a filter length equal to the number of data points, this is almost impossible without significant modification and transforming the filter into something completely different. We can make assumptions as to the weighting, but to use all of the data set to find one convolved result would imply that the weighting factors may not emphasize the close in points over the further distance ones.
Let’s assume that it is a symmetrical filter. at the first real data point in the series half of the values are zero. Just this action alone would imply that it would significantly suppress any values for the first 25% to 50% of the data points in the set. There goes your Medieval Warm Period. You would also suppress the final 25% to 50% of the filtered data set as well. Thus the replacement of the last years of the suppressed filtered with observations would allow Mann to correct for this suppression. Of course this id based on a symmetrical non causal FIR filter. Any skewing of the coefficients to the earlier side of the data set, and the suppression would last longer in the early sections with less run off issues at the end.
As an Electrical Engineer I would not use a filter of this width since the run on and run off data would bias the result too much. Also the phase change of the output would be too great to be of any use. This is nothing more than taking a weighted average across the entire data set and returning a single number. To be blunt this would be a worthless filter since too much data is lost, and too much invalid data is used in the calculation/convolution.
Martin, no. If I have a 50-tap filter I know my last 25 values are compromised and I cut them away. Now in Mann’s filter the “zero padding” is implicit, and basicly affecting the whole signal (except the middle value). So how many samples one is supposed to cut from the ends? It is not only the bending towards zero in the very end (which is the very last effect) but the artifacts last much longer (and actually contribute to the Swindlesque S-curve). You can easily see the effect by filtering a constant signal:
So the problem is that the zero-padding is implicit. The difference between a filter as long as the signal and one with only 50 taps is that there will be artefacts on all values except the middle one for the long filter, while the short filter will only have artefacts on the first and last 25 values.
My points was that in the case of the long filter, the artefacts on the values closer to center than 25 years from the ends should be small, since the tap values far away from the center should be low.
My comment about a long filter not being problematic in itself assumed that the filtered signal was of infinite length, which of course is not the case here.
Generally I think the only valid filter to use on time series like this is a rectangular FIR filter. This gives a value which everyone can understand, the average temperature of the last e.g. 30 years. And then it is clear that the last value which is valid is for the last 30 years, not the last 15 years and the comming 15 years, since we don’t know the temperature for the comming 15 years. If you want to use the average of the last 15 years you have to compare it to other 15 year averages.
We use this kind of filter on all other types of phenomena, e.g. the number of people killed in traffic every year would be based on an average of the last X years. You would never think of using a projection on future years in this average. Nor would you think of using some fancy IIR filter or a filter with some specific frequency domain characteristics.
I saw the plot now, and the ringing is substantial long after 25 years, so apparently the tap values are not small there. I take back my critique 🙂
U can even make a hockey stick
plot(lowmann(linspace(0,-0.2,998)’,2/40))
Zero padding would do that.
Nicely done Jean and UC. A graph is truly worth 1,000 words… 😉 .
Mann Smoothing Algorithm:
if (( ${measure} > ${predetermined_results_requirement_high} ))
then
(( measure=${measure} – ${measure}*0.02 ))
fi
if (( ${measure} < ${predetermined_results_requirement_low} ))
then
(( measure=${measure} + ${measure}*0.02 ))
fi
The theory and application of digital filtering is not especially difficult. Certainly there are many ways of doing it “essentially right” as well as innumerable ways of doing it terribly wrong. Too often a refusal on the part of an author to reveal exactly what was done has the main propose of concealing a kluged, ill-conceived “amateur-night” procedure and a basic ignorance of first-course DSP, even if not outright cherry-picking malfeasance.
However, doing the filtering OPERATION substantially right or ridiculously wrong should take a backseat to whether or not data should even be filtered in the first place. Filters improve coffee, and we call a coffee filter “good” when it gives us an amenable grit-free beverage. Filtering data modifies information. But of course we should not judge a data filtering attempt as successful (in the sense of properly chosen and implemented), or not, depending on whether or not we get an output that is agreeable to our prejudices.
Possibly another example where less is more.
I don’t think you stumble upon a filter like this out of ignorance. Ignorance would be to select a filter from an undergraduate text book and apply it in an improper situation. Rather, a filter like this is the result of sophisticated engineering and is designed to achieve a specific objective.
“…depending on whether or not we get an output that is agreeable to our prejudices.” I came across a quote recently that, in my opinion at least, is most worthy of sharing here at CA especially. I found this at a blog post to do with the Amplituhedron in particle physics and it emanated from Sean Carroll (Cal Tech, physics): “Always train your doubt most strongly on those ideas you want to be true.” (Michael Mann, et al., are you listening?)
Well, I post this so late in the game on this thread that most likely there will be few who will read it, but such is life.
I was looking at the Matlab script you posted. He’s using a convolution to perform the filtering on line 40 there. As others have noted, this effectively pads the input with zeros on both ends. Now, unless the input data is exactly zero at each end, there are going to be discontinuities (possibly large) at both ends of the effective input sequence where the zero-padding kicks in, and these will persist in time as “ringing” — at each end where there is a discontinuity.
I did a couple of experiments on that and it seems like it actually helps to create a hockey stick at the end — an artifact of the ringing in the low pass filter. Could this be another contributor to the stick?
Jean S: Yes, I believe it is a contributor to the Swindlesque S-curve, which is almost impossible to obtain with other methods even with the instrumental padding.
Note Observer’s post at WUWT August 30, 2014 at 2:17 pm:
I was wrong about dividing by “lw” — (lw-1) is correct…very minor point howvever and makes very little difference in the results.
Thx for correcting
Steve: Given the parsing you’re doing here on the filter, what about the method, which for 98 I thought was PCA. Maybe I missed any confirmation of provenience for it, but I recall the ‘father’ of PCA (i don’t recall his name) supposedly commenting either at BHill or here, or the comment being reproduced here, wherein he stated the given the description of Mann’s use of PCA, he (the father) could not determine what Mann had done!
Was this determined to be fake? I never saw any follow-up on the comment, nor confirmation or denial of authorship. If truly from the ‘father’ of PCA I would think it would be a more major and damning inditement of Mann than the filter question.
I think he came on to Tamino’s site (Tamino had been touting him as approving Mann’s centering ploy) and said that he had not at first had enough information to tell what Mann had done but now that he understood it, it was certainly not right.
Was it confirmed to be the correct person? If so, isn’t that fairly damning, and why isn’t it a bigger point NOW given Mann’s claims of math expertise???
CJ (5:11 PM):
Sadly Harold Hotelling died in 1973 so I doubt he contributed to the blogs mentioned in the way described.
Was the person who commented on Open Mind purporting to be Hotelling, or another PCA propitiatory. Wondering if anyone knows the blop the comment was posted to?
It was Ian Jolliffe, here.
Jolliffe was described originally by Tamino as “one of the world’s foremost experts on PCA, author of a seminal book on the subject” and I don’t think people on CA were inclined to disagree. But that’s rather different from being the ‘father of PCA’.
I remembered Hotelling as the journalist (and thus amateur, rather like our host) who came up with PCA as well as Canonical Variate Analysis. As I remember he introduced PCA in his 1931 The Generalization of Student’s Ratio, worthy of inclusion in the first volume of Breakthroughs in Statistics: Foundations and Basic Theory by Kotz and Johnson. His Analysis of a complex of statistical variables into principal components was 1933.
On googling to check the details last night it was striking that Wikipedia seemed hesitant to give credit to someone initially so uncredentialed, saying “PCA was invented in 1901 by Karl Pearson”. Pearson was an academic insider who believed all the right things, being a “major proponent of eugenics” and “a protégé and biographer of Sir Francis Galton”. Hotelling isn’t mentioned on the main PCA page, though a couple of dissenters put forward his claim in the ‘Talk’ page.
It makes me wonder what they’re going to be writing about McIntyre and colleagues in eighty years.
I’d like to take this opportunity to advertise that Octave now (starting from version 3.8) has a nice GUI. Windows binaries available here.
Excellent. (Apart from the mention of Windoze!)
Yes, I included the reference to Windows binaries as they are a bit hard to find. Linux users probably already have a version with the GUI, just add –force-gui when starting Octave (GUI will be the default starting from version 4.0, now it is considered “experimental”).
I try not to comment on technical posts but would appreciate if someone could demonstrate the effect of what Mann did using a non-climate issue.
i.e a worked example please sir:-)
It appears to me that what we have had here on this thread are several electrical engineers and those familiar with circuit filtering methods weighing in on what these various filters do with a noisy signal, but what “works” for an electrical signal is not necessarily connected to the best way of presenting a time series at least in this layperson’s view. The important elements of interest in a times series of global and regional temperature or supposed temperature reconstruction are the decadal trends that might exist in the series and determining in what time periods in the anomaly series the higher and lower extremes occur.
I am certainly no expert in filters and applications of filters but are not their a few limited choices of standard filters that might be appropriate for these temperature reconstructions and whose operations are reasonably well understood , e.g. a simple moving average or a spline smooth or a lowess filter or exponential smoothing. What would motivate an author of a study move away from the more standard methods of smoothing in order to show decadal trends and extended peaks and valleys in the series.
Steve: I agree entirely. part of the problem is that “signal-noise” is a metaphor when applied to climate series, but too often the metaphor is reified by climate academics.
Kenneth,
First we Electrical types have experience in more that just electrical valued signals arranged in a time series. Many of these functions that are used were developed long before the advent of computers. Bessel, Chebyshev, and Fourier developed their theories and equations long ago. Personally, I have used these functions to remove high frequency components of measured data from various manufacturing processes. This was to see trends over longer periods of time that could not be easily elucidated from the base graph. The problem is loss of data and limits at the edges of the data set. So basically you use methods best suited the information you are looking for.
I am not a climatologist, but as an engineer I use time series data on a daily basis. We model, test, and then confirm the model with that data. Data analysis is data analysis, whether it was 100+ years ago or yesterday. There are correct and incorrect methods and reasons for applying a filter. As long as the raw data and methods used are freely available then everyone is on the same page and reverse engineering of the results are not necessary. If however the intent is to hide what you are doing and cause significant damage to the data using methods that distort the result, then yes there are methods that should not be used. There is no transparency in this “Hockey Stick”, and in my world I would be fired for such methods.
I cannot speak to Mann’s motivations, but the methods he used were, if the above is accurate, speaks to either incompetence or malfeasance. Maybe during his trial we will find out, for discovery works both ways. Electrical Engineers use closed loop control systems and signal processing to provide many modern conveniences. Unlike some in the Climate Science Realm, if it does not work no one will buy it and we Engineers would be out of a job. So we do have a bias for what works and not much tolerance for methods that will cause errors. Error is bad, accuracy is good, and what this method is doing is causing error and no matter the motivation, Mann was heading in the wrong direction.
Yes. The ‘electrical’ signal might be the concentration of a gas in a pipe or the pitch of an airplane. These ‘electrical signals’ are used well outside of the realm of electrical measurements, as well as on actual electrical measurements. We basically don’t do pneumatic or other mechanical instruments any more. They’re all electrical, but voltages and currents are proxies for all kinds of meaningful physical measurements.
It’s a distinction without a difference.
Kenneth Fritsch, I prefer Butterworth filters, implemented similar to the “filtfilt” algorithm in Matlab, over simple running averages. FIltfilt, which I believe Mann uses now, also does things like pad using the reflection about the starting and end points of the data series (this extends the trends near the end points, to the end points). Some discussion of this here.
Don’t get stuck on what you can do with “circuit filtering” either… these are necessarily physically realizable filters. Non physically realizable filter schemes like acausal filters (which are available to use for off-line processing) have superior characteristics to what can be achieved by analog implementation of filters (e..g., Sallen-Key).
If you look at the frequency response of a running average, it is very poor compared to e.g. a fourth-order Butterworth. You really want to suppress the high frequencies (above your corner frequency), because when you smooth with a low-order filter like a running average, signal components associated with these frequencies are still visible, but they often appear with the “wrong phase”. Butterworths, like most recursive filters, often have very few taps. This means that the end effects associated with the Butterworth are small.
So if you’re going to smooth, using a decent quality filter is important.
I regard the Michael Mann who published his original papers to be in practice a novice at signal processing. I wouldn’t describe what he has done as anything worse than clumsy and suboptimal.
(I think “clumsy” is a very good word indeed to describe poorly executed code. There is also “clumsy and stupid”, which is a bit worse than just being clumsy, that occurs before we start suggesting malfeasance. )
Thanks, Richard P and Carrick for your informative replies. For my purposes I would probably be better served by constructing a synthetic series with known amounts of white and red noise, cycles and deterministic trends and then applying a filter to determine how well it better represents signal features of interest in the smoothed series than in the noisy rendition. I would think that a filter that leaves residual noise is better than a filter that produces or could produce artifacts.
I also wonder whether a stochastic trend in a time series caused by red noise with substantial autocorrelations can always be differentiated from a deterministic trend or whether one can only point to the probability of the red noise causing an indistinguishable trend.
Finally I am not sure I understand the magnitude of the effects of using instrumental temperature data to pad the smoothed reconstruction series. It gets my dander up whenever I see instrumental data intermixed with proxy responses as though we can assume that instrumental and proxy responses were on the same level of reliability in measuring temperatures. I then see references to house cleaning which I assume is implying the problems found in this effort are not game changers with regards to the reconstruction results but rather pointing to bad to inadequate methods used.
Kenneth Fritsch, if you’re concerned about the issue with ringing, claiming that Butterworth’s ring and running averages don’t… that’s a bit of a red herring.
How much ringing you get depends chiefly on the order of the filter (or equivalently, dB rolloff per octave).
For impulsive signals, you need to use a lower-order filter to reduce how much ringing you get. Typically, the trade-off with order of filter is how much ringing in the time domain you get versus ripple in the frequency domain.
Note you can reduce the amount of ringing/ripple with more complex filter designs with the same dB roll-off, so this should be seen just as a rule of thumb.
The bigger issue for impulsive signals is that acausal filters such as that used with FILTFILT produce artifacts before the signal has arrived. For asymmetrical impulsive signals (e.g., shockwaves from explosions with long tails). If you’re filtering broadband continuous signals, ringing hardly matters, but ripple is a bigger issue. In that case, a higher-order filter is generally desirable.
These are just rules of thumb. The specific application influences filter choice too (audible sound, image filtering, etc.), so generally relying on the accumulated wisdom in a particular field for “what works best” would be a better practice than just trying to use some generic filter design everywhere.
Kenneth Fritsch:
I think you should never pad proxy data with the instrumental data before filtering. When it’s done to deceive the reader about the quality of the reconstruction, e.g. to “hide the decline”, that amounts to scientific fraud, IMO.
Carrick, I am sure from reading your posts here and other places that you know your frequency domain of time series and analyzing time series in general. My problem as a layperson is relating these filters use for signal processing to what I know I would want to visualize from a filter smoothing out the noise in a temperature time series. Was not Mann’s purpose in using a smoothing filter on his reconstruction series a matter of better visualizing longer term features and trends?
Kenneth Fritsch:
Yes, that’s the usual purpose for smoothing/low-pass filter: To remove high-frequency noise from the time series, while minimizing the artifacts produced by the smoother. While it’s popular and highly efficient if implemented properly, I do not think a simple running average is an appropriate smoother for this application.
If I were to recommend a smoother for this sort of application, I would suggest a 4-th order Butterworth that emulates filtfilt. This includes forward-backwards implementation plus reflection about the end points. It’s worth noting that if you are interested in a smoothed series with a resolution of 10-years between points, your filer design should have a roll-off at a frequency of 1/(20 years).
Again, I’d encourage you to read the older post from Climate Audit. It contains some good discussion (though unfortunately the inlined images are missing).
I believe there is an R-code by UC (?) that emulates the Matlab filtfilt function.
Steve: filtfiltx by Roman Mureika
Not by UC…
… and the emulation does it by bypassing a complicated calculation of the padding sequence used by Matlab so the only padding needed is with a sequence of zeroes.
🙂
Thanks, Carrick, that gives me a starting point for filtering some synthetic series where the underlying signal is known.
Steve & Roman, thanks!
Here is a link to filtfiltx.
I might add that I installed the latest version of Octave yesterday and ran their example for Matlab filtfilt. After porting the data to R I compared Octave filtfilt to filtfiltx. The latter was identical to Octave’s results within 1E-14. However, R’s filtfilt had seriously large endpoint differences from these results.
They should fix the R version.
(1) The Matlab code provided by Jean S produces a linear phase (zero phase properly shifted) impulse-response that is indeed as long as the signal. BUT, when we look at the impulse response (the “b” output), it is very tiny except close to the middle, a fact that results from it being calculated from a sinc function which already roll-off rapidly away from the center, further tapered to 8% at the ends by the Hamming window. Effectively, it is much much shorter. It is not clear that a full length filtering result, SHOWN AS A PLOT, would be detectably different from one of say, just using the 10% of the taps near the middle. Anyone tried this?
(2) The use of the IIR Butterworth, truncated, and made linear phase by “filtfilt” is probably AS suspect as Mann’s effort. Much more sophisticated and far better defined (and direct) FIR design methods exist (such as minimizing weighted integrated squared error in the frequency domain to achieve a flat passband – Matlab “firls”). I doubt very seriously however, that any of these alternatives relegates Mann’s poor filtering effort to the “smoking gun” class, especially relative to sins of non-disclosure and suspicion of cherry-picking of data and outcomes. Steve called this thread “housekeeping” and I agree.
(3) Others have advocated for the “no filter” option, and insisted that filtered data are no longer even data. Quite true. I would add to this an insistence for examining ANY proposed time-series smoothing filters extensively, using MADE-UP test data (red signals, sequences of all ones, trapezoids, ramps, sinusoids) to see what mischief the filter does that you never suspected.
Bernie Hutchins:
I haven’t tried it, but your suggestion seems sensible. You only need to retain enough taps that any artifacts associate with the truncation get buried in the noise.
I’d be curious what you think is suspect about Butterworth filters for this application. Is it because it is recursive, or is there something in the pole structure of the Butterworth filter?
It seems to me this is a very well-studied algorithm as used in the Matlab code, and I think is robust when applied using filtfilt or similar end-point processing.
Why FIRs? They don’t seem appropriate for this application due to the amount of padding you need to do… end-point effects matter here. Recursive (IIR) filters greatly reduce how many taps you have, and reduce the end-point effects.
Yes it’s not a “smoking gun”. A poor quality effort yes, but not really wrong.
Carrick – Thanks for your comments. I pretty much agree with you on everything.
As for filtfilt, I consider it as essentially an FIR design method because it provides a center-clustered impulse response not at all unlike a sinc, etc. Try for example the one-liner:
stem(filtfilt(butter(4,.25),a,[zeros(1,49),1,zeros(1,50)]))
and you will see what looks like just about every other reasonably good FIR low-pass impulse response. I like it. But you do have to truncate it (like from 35 to 75), which is not a problem. (By the way, I think Jim Kaiser originated this idea as what he called “twiceing”, but can’t find a reference.)
The problem is that I know I can do just a bit better with the minimized integrated frequency domain squared error procedure (Matlab’s firls), which is self-truncating and optimizing.
But this tiny improvement is NOT significant, and you are quite right in saying: “…..end-point effects matter here….”
I was not clear in saying that it was these end transients which I thought “suspicious”. I kind of doubt there is any LTI filter that will not mess up the ends. I like something that shortens the length as you approach the end (run out of data).
All these time-series smoothers need to be tested with artificial data, as Kenneth Fritsch suggested he wanted to do above. I suggest finding something that leaves noise-free rectangles and ramps virtually alone. Then try adding noise. Finally real data. It may never work.
In looking at end effects, avoid Matlab’s filtfilt or even filter (which mess with the ends), and stick with conv (first computing the IIR impulse response USING filtfilt as I suggested above).
Thanks for the comments Bernie.
Regarding this:
I have code dating back to 1994 that does this, and I’m pretty sure I learned this from a mechanical engineer that working our group at the time. So it’s been around for a while.
I’ve also experimented with different types of end-point treatment. Zero-padding is a terrible idea of course. But I also did polynomial detrending followed by filtering, padding with the end-point value (on both ends) and reflection about the end-point.
Depending on application, either padding with the end-point or reflection works better. If you have a maximum or minimum (or when there is curvature in the real data series) near the edge, end-point reflection causes overshooting (or undershooting) from the real signal.
Michael Mann probably likes end-point reflection better because it suggests that a trend is still present near the end point (but practically we can’t actually know without taking more data). Before the pause, it was “obvious” to most people that preserving the trend was the right way to filter, as opposed to padding the end. However, I’ve always argued “stop when you run out of points if the answer near the edges matters”. (Don’t pad.)
I also tried using FIR filters, and reducing the size as you approach the end-points. As you might suspect, for noisy data, this also produces “unsightly artifacts” near the end points (the noise increases as you approach the end point of course).
Life is just much easier when we can collect extra data, then chop a bit off the edges after filtering. When I do laboratory measurements, that’s how I generally handle the end-point problem.
Steve: Mann sometimes uses another end point padding: double reflection- after reflecting on the x-axis, reflect on the y-axis at the closing endpoint.
Steve McIntyre:
Yes, this is called “reflecting about a point”, which is what I mean when I say “reflection about the end-point”.
For sake of clarity, for a reflection about the y-axis going through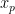 , we have:
, we have:
so the reflected point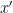 is:
is:
Reflection about a line through follows mutatis mutadis.
follows mutatis mutadis.
For a reflection about a point , we then have,
, we then have,
One could also do reflection about the y-axis at the end-point, but I’ve never found that to be satisfactory. If there is any trend near the edge, this forces the smoothed curve to have a local maximum at the edge-point. I would say that is rarely justifiable.
Carrick –
Indeed your formula x’=2xp – x is, (in the discrete time case, which is certainly the major interest here):
x’(n+1) = 2x(n) – x(n-1)
which is simply a matter of stating that the slope continues (a first-order “projection”). You can then first-order project the slope and arrive at
x’(n+1)=3x(n)-3x(n-1)+x(n-2).
Continuing we project the change of slope and get:
x’(n+1) = 4x(n)–6x(n-1)+4x(n-2)–x(n-3).
Yes, the pattern of alternating binomial coefficients with the first one missing continues. And all these FIR filters have zeros with real part 1/2. A lovely result – that means almost nothing as far as I know! I discovered this myself 28 years ago, and have never used it – except as a homework exercise.
Like most smoothers that impose structure, potentially you can rediscover the structure you imposed and fool yourself into thinking it means something. Carrick you said: I’ve always argued “stop when you run out of points if the answer near the edges matters “. (Don’t pad.)” Sound advice.
Thanks Bernie, interesting comment!
The “One-Line” Matlab suggested in post above worked (for me) by accident! Apologies. And probably few have Matlab anyway, so here is a fuller worked example:
This illustrates that filtfilt designs essentially an FIR filter, as “firls” does. Code that made pictures is below the four figures.
The “end correction” that is obtained using filtfilt for actual filtering can almost certainly be used for any FIR design. It is not unusual that methods converge.
Bernie, your comment (from September 6th), i.e., “. . . all these FIR filters have zeros with real part 1/2. A lovely result – that means almost nothing as far as I know!” prompted my memory of the Riemann Hypothesis, a proof of which is the current Holy Grail in prime-number theory (and much besides): “The nontrivial zeroes of the Riemann zeta function all have real part equal to 1/2.” As I recall, the conjecture applies to “local” Zeta functions. Perhaps your “lovely result” means something after all!
Just sayin’.
FYI: I am a (retired) physicist who dabbles in complex analysis and knows next to nothing about digital-signal filtering.
“Why FIRs? They don’t seem appropriate for this application due to the amount of padding you need to do… end-point effects matter here. Recursive (IIR) filters greatly reduce how many taps you have, and reduce the end-point effects.”
I don’t think so. IIR is just to hide the end-point effects
UC:
We are interested in the series near the end-points, and FIR requires an excessive amount of padding for this application. You can reduce the number of taps (the filter length) using IIR filters.
Hence this reduces the number of points near the end-points affected by the smoother. This isn’t a matter of just “hiding the end-point effects”, using IIRs actually reduces it.
Here my initial responses are in { }. Detailed comments below the quotes.
Carrick commented above:
“Why FIRs? They don’t seem appropriate for this application due to the amount of padding you need to do… end-point effects matter here. Recursive (IIR) filters greatly reduce how many taps you have, and reduce the end-point effects.” {False}.
To which UC responded:
“I don’t think so. IIR is just to hide the end-point effects.” {Also False}.
Carrick then replied to UC:
“We are interested in the series near the end-points, and FIR requires an excessive amount of padding for this application. You can reduce the number of taps (the filter length) using IIR filters.
Hence this reduces the number of points near the end-points affected by the smoother. This isn’t a matter of just “hiding the end-point effects”, using IIRs actually reduces it.” {Nope}.
Misconceptions all around here! Two comments in clarification.
(1) An IIR filter needs fewer coefficients (path multipliers) relative to an FIR filter for a comparable sharpness of performance in the frequency domain (narrow low-pass transition band, band-pass width, etc.). But, you will need approximately the SAME significant length of the actual impulse response. (See my graphs at Sept. 7, 11:28 AM). Do not confuse number of coefficients with the length of the impulse response. They ARE the same for FIR but not for IIR of course. This is just Fourier transform stuff (z-transform or Discrete-time Fourier transform actually), and the corresponding “Uncertainty relationship”. If delta-f gets small, delta-t must get larger. No equivocation. The FIR version has a “coefficient” (path multiplier) for each value of the impulse response. The IIR design has fewer coefficients (smaller by a factor of 5 or 10) for a similar performance. See again link below, pages 19-20):
Click to access EN198.pdf
But if you look at the most significant portion of the IIR’s impulse response, it will be about as long as an equally performing FIR. IIR has NO ENDPOINT ADVANTAGE. So – Why are some misled in this regard?
(2) The Malab function “filtfilt” is not restricted to IIR. It is in fact often used for IIR (like Butterworth) because we may want to arrive at linear-phase. So this brings up a second point. A filtering ACHIEVED from IIR using filtfilt may APPEAR to have fewer endpoint problems than FIR. But this is due to the refinements at the conclusion of filtfilt for treating ends. It’s artificial and misleading. Use the full convolution, not “filter” or “filtfilt”.
I understand what you are saying, but consider the case where you’re using a shorter-length IIR filter with padding and you cut it off at the original end-point before padding.
I’m pretty sure it is the case that you’ll end up a smaller end effects with the shorter filter, even though the general point you are making about the length of the impulse response function of the filter, compared to what you would get with a traditional FIR filter.
Obviously this is not a general result of IIRs (you can’t use forward backward filtering for example), but because we’re discussing truncating the IPR, you can in principle (and I think) in practice end up with a shorter region near the end point influenced by the filter.
* even though the general point you are making is correct about the length of the impulse response function …
Reblogged this on I Didn't Ask To Be a Blog.
I plan to continue my work with synthetic data and various filters for my own edification in this matter. What becomes very apparent as critical to modelling a temperature series (in this case the land/ocean GISS global mean annual adjusted temperature) is how one chooses to detrend the series which in effect means deciding what variations are natural and part of the red noise or cyclical structure and what part is a deterministic trend and further what is the shape of the deterministic trend. On detrending the GISS series with a linear regression over the period from 1880-2013, an ARMA model requires a fourth ordered ar to obtain the best AIC and Box.test p.value.
On further thinking, I suspect one would want to remove the white noise from these series and determine what is left in the form deterministic trends and red noise/cycles. Assumptions would then have to be made about the variations due red noise and cycles. I suspect the best a good filter could do would be to remove the white noise – and that would be for appearance purposes of a graphed series and not for analyses purposes. I think that cycles are going to be included in the ar part of the ARMA model, although I would suppose the cycles, if sufficiently short, could be estimated from a frequency analysis for instrumental data.
As an aside I continue to think that its very wrong to use instrumental data to pad a series and more than wrong not to state that it was used for padding.
In my preliminary analysis using the global mean land and sea adjusted GISS temperatures from 1880-2013 as a basis, I find that using various smoothing splines works well for me in smoothing and estimating the white noise and in turn estimating the red noise by difference. Smoothing splines also work well in estimating trends in these series that are not necessarily linear and thus making detrending more realistic for subsequent modeling of the residuals. Detrending, of course, requires some independent input and assumptions as to the expected shape of the trend line.
I would think that a properly chosen smoothing spline would give a reasonable presentation of temperature and proxy response series.
As an aside I could find no cyclical structure of statistical significance in the power spectrum of the GISS temperature anomaly series.
I have been aware of the influence the detrending curve has on the model derived from the residuals and the following example illustrates it well. As noted previously using the residuals from a linear regression of the GISS global mean from 1880-2013 results in a best fitting model of ARMA(4,0) with no statistically significant cycles in the residuals as estimated from a smoothed power spectrum. Now using residuals from the same GISS series and a 5th order spline smooth to define the trend produces a best fit model ARMA(1,0) and with a smoothed power spectrum showing significant cycles at 3.5, 5, 8 and 60 years. The smoother used in this case to define the deterministic trend was one that fit very well, qualitatively, if not quantitatively, the published estimated effects of GHGs and aerosols on global temperatures.
As an aside a 1000 member simulation of the ARMA(1,0) (ar=0.41) series with a standard deviation of 0.0856 with no trend added yielded 19.4% of 975 possible 25 year periods with a statistically significant trend. The mean absolute value of the trends was 0.61 degrees C per century. The residuals of the ARMA series (white noise with no added trend) had 3.5% of the possible 25 year periods with statistically significant trends with an absolute values of trends of 0.51 degrees C per century. It shows that it is not difficult to select a proxy response that can have 25 year periods of significant and modern era instrumental-like temperature trends from a series containing no deterministic trend but rather only red and white noise.
Kenneth –
So you propose to do deliberate, honest, and transparent research! How do you expect to GET the results you WANT? No Nobel Peace Prize for you.
Related to smoothing, I asked Tom Parks about Kaiser’s “Twicing” (with Hamming – back to 1977) and he sent the link:
Click to access filt_sharp.pdf
which unlike most IEEE stuff, is free. The same method is described by Rich Lyons in his book (3rd edition pp 726-728) and is quite interesting to compare to filtfilt.
5 Trackbacks
[…] Bold mine. Read more here: https://climateaudit.org/2014/08/29/mannomatic-smoothing-technical-details/ […]
[…] JeanS adds in a comment: […]
[…] Date: Aug 29 2014, Jean S nails it, […]
[…] Mannomatic smoothing details […]
[…] of Figure 5b. This has been covered here so many times (for the exact parameters, see here), that I just show the “before” and “after” pictures as they seem popular. […]