Climate Audit

I previously posted up two comments on our Reply to Huybers here and here, the first of which contained some new material. Here’s the third and final instalment, discussing Huybers’ comments on principal components. While principal components were really only one aspect of our critique, the reaction of the Hockey Team and the “community” to our studies has been almost entirely to the principal components issues.

In my opinion, we have always stated quite clearly that there is an inter-relationship between data and methodology. The flawed MBH98 method seeks out the most flawed proxies (bristlecones), creating a “perfect storm”. Our attention was originally drawn to the bristlecones by following the flawed method back to see what it did, finding to our astonishment that it unerringly picked out the controversial bristlecones into their PC1. But once you are aware of the presence of the flawed proxies, you can’t simply try to patch the methodology if the patch still results in the flawed proxies dominating or even materially affecting the final result. And yet this is what the Hockey Team and the “community” consistently does — always in the name of some supposedly “correct” PC methodology e.g. their misapplication of Preisendorfer’s Rule N (previously discussed on this blog). In all this time, I have yet to see any serious attempt by the Hockey Team or the “community” to defend the bristlecones as a temperature proxy. This is always set out as a topic for “future research” e.g. Huybers.

Huybers’ counter-critique of our principal components analysis is based on a difference between covariance PCs and correlation PCs. I pointed out that Huybers had said in private correspondence that it was unsatisfactory that world climate reconstructions should rest even in part upon fine methodological distinctions such as this, but this did not prevent him from presenting this as a criticism of our article — without acknowledging the point made in private correspondence.

Covariance and Correlation PCs

Here is a discussion of the difference between correlation and covariance PCs, starting with some background and ending with Huybers’ discussion.

My interest in the MBH98 PCs obviously began right at the beginning. MBH98 said only that they used “conventional principal components” methods. In our first go at this in McIntyre and McKitrick [2003], we reported on our inability to replicate their PCs using conventional methodology. The illustration in McIntyre and McKitrick [2003] was actually from the Australian network, not the North American network which has been the focus of so much recent discussion. I’ve replicated the figure from MM03 to show that the issue was raised quite early (although we could not then figure out what Mann et al. were actually doing with their PCs.)

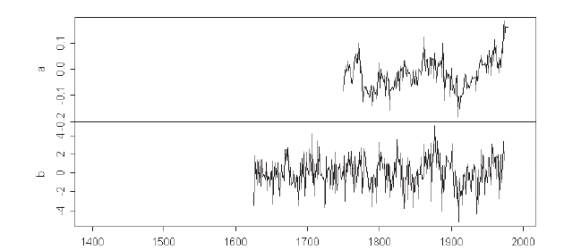
MM03 Figure 5. PC1s from the MBH98 AUSTRAL network: top – MBH and bottom – princomp.

In doing a principal components analysis using the standard algorithm princomp from R or S, the default option is a principal components analysis on the covariance matrix, with principal copmonents on the correlation matrix being a secondary option. We experimented with both options in an attempt to replicate the MBH98 PC series to no avail and, of course, Mann was unresponsive to our inquiries on his methodology both before and after publication of MM03.

After the publication of MM03, an FTP directory on MBH98 suddenly materialized in November 2003. Although Mann refused to provide source code, by chance, he had left Fortran code for his tree ring PC calculations in this directory – code for other steps was not available until another dump took place in response to the Barton Committee request, but the archived code is still incomplete as I discussed in the summer . By analysing this code, we discovered in December 2003 that MBH98 PC calculations involved short-centering, which we ultimately reported in our GRL article published in early 2005.

In order to demonstrate that there was an actual difference between the PC series (which surprised many people), in Figure 3 of our GRL article, we illustrated the MBH98 PC1 against the PC1 resulting from the default option in a standard principal components algorithm – a diagram not disssimilar to our earlier diagram in MM03 for the AUSTRAL network.

MM05a Figure 3. PC1s from the MBH98 15th century NOAMER network: top – MBH and bottom – princomp.

By doing so (and this is a nuance that the “community” seems to have trouble understanding), we did not in any way suggest that a “conventional” PC1 had any climatological significance or was in any way a magic bullet to extract usable information from the controversial North American tree ring network. All that we intended to show was what the PC1 looked like if you calculated it the way that MBH98 said that they did it, thereby showing that the PC1 was not “robust” to changes in centering. We certainly did not advocate that the covariance PC1 as “our” methodology or as a way of “removing the bias” in MBH98 (suggestions made by Huybers.)

This Figure was relevant to our argument, but the point illustrated in the figure was not one that we identified as sufficiently prominent to include in our Abstract (where we discussed the bias of the PC method, the selection of the bristlecones, the failure of MBH98 cross-validation statistics and the spuriousness of the high RE statistic).

Huybers’ Comment

In his Comment, Huybers agreed that the MBH98 PC method was biased, but then said that we attempted to “remove the bias” in MBH98; that, in doing so (in what he called “MM” normalization), we used a “questionable normalization” procedure; and, that we “exaggerated the bias” of the MBH98 method. Needless to say, we disagree with this language on a couple of counts.

First of all, we did not try to “remove the bias” in MBH98. We’ve made it abundantly clear that we do not adopt MBH98 proxy selection and have no commitment or belief to the view that applying a mechanistic algorithm like principal components is any guarantee that a temperature “signal” can be extracted from the North American tree ring network. We made this abundantly clear to GRL editors, but in the Famiglietti regime, this fell on deaf ears. We objected to the description of the covariance PC1 as the “MM normalization” — we had no objection to Huybers describing this in objective terms, such as “covariance PC” and suggested this to GRL, but again this fell on deaf ears.

But the one that grated most was the suggestion that we used a “questionable” normalization procedure. Huybers argued that correlation PCs were the “correct” PCs, citing two statistical texts — Preisendorfer [1988] and Rencher [1995] as authorities, but without any page references. Huybers:

Thus, a third normalization is proposed where records are adjusted to zero-mean and unit variance over their full 1400 to 1980 duration, a standard practice in PCA [Preisendorfer, 1988; Rencher, 1995] here referred to as full normalization.

We were unable to locate any support for the idea that covariance PCs were “questionable” in these texts. In fact, the statistical authorities clearly favoured covariance PCs when the data set was in common units (such as tree ring networks in common dimensionless units). We pointed this out both to Huybers and to GRL, requesting a valid source for the contention that these authorities supported correlation PCs in the given circumstances as follows:.

Both citations are texts, yet no chapter or page citations are given. The reason, I suggest, is that it would be impossible for Huybers to provide a direct quotation from either authority on this point because they do not support the procedure Huybers proposes in the context of series already in dimensionless units with a common mean. In fact, their explicit statements run in the opposite direction. As a general matter, it is simply false that scaling to unit variance is a “standard practice in PCA” for data sets already standardized to dimensionless units with a common mean. The onus is on Huybers to back up this claim. Neither of his authorities do so. He should either produce explicit support, such as a chapter and page number or remove the claim. The onus should not be on us to use up our word limit providing extensive quotations from his own sources to show that they do not support him.

Again we met with no success from either party. Here’s what the authorities actually say (and this next section is pretty much verbatim from a letter to GRL).

Rencher [1995] stated almost exactly the opposite of what Huybers claimed for data sets in common units, but with different variances as follows:

Generally extracting principal components from S [covariance] rather than R [correlation] remains closer to the spirit and intent of principal component analysis, especially if the components are to be used in further computations. (p. 430)

This follows almost verbatim a similar comment in Rencher [American Statistician 1992, 46, p 221], which said:

“For many applications, it is more in keeping with the spirit and intent of this procedure to extract principal components from the covariance matrix S rather than the correlation matrix R, especially if they are destined for use as input to other analyses. However, we may wish to use R in cases where the measurement units are not commensurate or the variances otherwise differ widely.”

The exception contemplated by Rencher [1992] is a circumstance in which a few series measured in different units have much larger variance than the bulk of the data, because it would dominate the analysis:

“When one variable has a much larger variance than the other variables, this variable will dominate the first component”.

This is the exact opposite situation to MBH98, where two density series have much smaller variances, and moreover are from sites already represented by width series in the major partition of the dataset. It is clear in context that Rencher would not prescribe the normalization Huybers proposes.

Preisendorfer, in Overland and Preisendorfer [1982], admittedly a slightly earlier reference than the posthumous Preisendorfer [1988], stated, again in direct opposition to Huybers:

In representing the variance of large data sets, the covariance matrix is preferred” (p.4)

I have not found a comparably explicit statement in Preisendorfer [1988]. However, this text nearly always talks in terms of “covariance matrices”, rather than “correlation matrices”, such as the following quote in our Reply to Ritson:

The first step in the PCA of [data set] Z is to center the values z[ t,x] on their averages over the t series… If Z… is not rendered into t-centered form, then the result is analogous to non-centered covariance matrices and is denoted by S’. The statistical, physical and geometric properties of S’ and S [the covariance matrix] are quite distinct. PCA, by definition, works with variances i.e. squared anomalies about a mean. (p. 26)

Preisendorfer [1988] never suggested a change from the position of Overland and Preisendorfer [1982], which is cited approvingly on several occasions. The standard examples in Preisendorfer [1988] apply to PCA on data sets (e.g. sea surface temperature, sea level pressure defined over regions), which are not scaled to unit variance. The procedures are described in detail and, while Preisendorfer explicitly calls for centering over the time average, he NEVER calls for scaling to unit variance on these data sets which are in common units but have differing variances. This is the exact parallel to the data set we analyse. Preisendorfer discusses the covariance matrix on virtually every page, but only mentions a correlation matrix on a couple of occasions. The only occasion in which Preisendorfer calls for scaling to unit variance is when a data set is a composite of two data sets denominated in different units, e.g. sea surface temperature in one region and sea level pressure in another — which is not the case in the dataset under discussion here as discussed above.

We were never given a specific page reference in Preisendorfer or Rencher by Huybers or GRL in response to our request. In Huybers’ final accepted comment (which we did not see during the preparation of our final reply), he changed the citation to a new edition of Rencher and did provide page references to Preisendorfer and Rencher, which describe the correlation PC, but do not provide any support for his contention that the covariance PCs were “questionable”.

In our first draft Reply, we attempted to dispute some of Huybers’ points of this type, but were required to delete such language, being told that concerns about mischaracterization would be dealt with editorially (which they weren’t).

Correlation PCs
I think that it’s pretty evident that the statistical texts do not support correlation PCs relative to covariance PCs. However, do correlation PCs, for whatever reason, actually yield a “correct” result? We provided a variety of arguments on this topic in our Reply. I’m not sure that these points come across all that clearly in the compressed format of a GRL reply, so I’ll expand a little here.

Huybers argued that the correlation PC1 was a better approximation to the simple average of all 70 series than the covariance PC1. This fascination with “approximating” the average baffles me. Ritson got involved in the same thing. If you want the average of 70 series, then just calculate it. You don’t need to do a PC approximation. So if there’s some purpose to a principal components calculation, it would have to be different. We hypothesized some potential purposes to show that the correlation PC1 was no magic bullet.

The 70 sites in the 15th century network are only a subset of the 212 sites in the full network. One possible purpose of using a “PC” analysis would be to obtain an indicator that empirically approximated the average of all 212 sites — using only the 70 sites available in the 15th century network. If you did this, you found that empirically the covariance PC1 was a much better approximation to the 212-site average (introducing each site as available) than the 70-site average. So why would you use the correlation PC1 to approximate the 70-site average?

Another interesting argument pertained to calculating standard deviations for tree ring series, which are highly autocorrelated. I pointed out in a post in August, that may have seen a little abstract at the time, that sample variances for highly autocorrelated series massively under-estimated the true variance of the process. This is a topic that interests me in light of the attempts of people like Esper to bypass regression theory by “scaling” series — which I think boils down to having similar problems. In our Reply, we calculated variances using a “heteroskedastic-autocorrelation consistent” variance estimator from econometrics. Again, empirically, this led to a result very similar to the covariance PC1, rather than the correlation PC1.

We pointed out that another approach to calculating a PC series might involve weighting the series for area or species. The 15th century network contained 16 sites from one gridcell (the one containing most of the bristlecone sites) and only 1 site from other gridcells — area weighting would also downweight the bristlecones.

The difference between the correlation PC1 and the covariance PC1 boils down entirely to a greater impact of bristlecones in the correlation PC1. If there was a problem with the bristlecones as a proxy, then there was no statistical rule that said could say that you had to give them more weight in the index. Huybers simply dodged this issue, saying that this was a topic for “future research”. Our reply to this was that it was pretty late in the day for this — MBH98 had represented careful proxy selection and the “research” to show that bristlecones were a valid temperature proxy should have been done long ago.

Huybers’ Figure 2
Huybers presented a Figure supposedly showing that the MBH98 PC1 was not as bad as indicated in our Figure 3. Before considering this figure, I’d like to re-emphasize that our fundamental criticism of the MBH98 PC method was its bias as a method in yielding hockey stick shaped series — this is a different issue than the impact of the method on a specific dataset. Our critique of its impact in the NOAMER dataset was its overweighting of bristlecones and thence a critique of the bristlecones themselves as the dominant imprint on the MBH98 hockeystick.

Huybers did what seems to me to be little more than a rhetorical trick to supposedly demonstrate that we had “exaggerated the bias”. For his Figure 2, he re-centered the various PC1s on the 1902-1980 short segment. The covariance PC1 and correlation PC1 are pretty comparable for most of their history, but the correlation PC1 goes up a little more in the 20th century because of the extra weight of the bristlecones. By short-segment re-centering, Huybers makes it look like the covariance PC1 is anomalously negative. If you do the same diagram centering on 1400-1980, you get an entirely different appearance.

We did a version of Huybers’ diagram in our Supplementary Information, shown below, centering the correlation and covariance PC1s on 1400-1980 – instead of short-centering on 1902-1980, and using the 212-site average as comparandum, rather than 70-site average. T

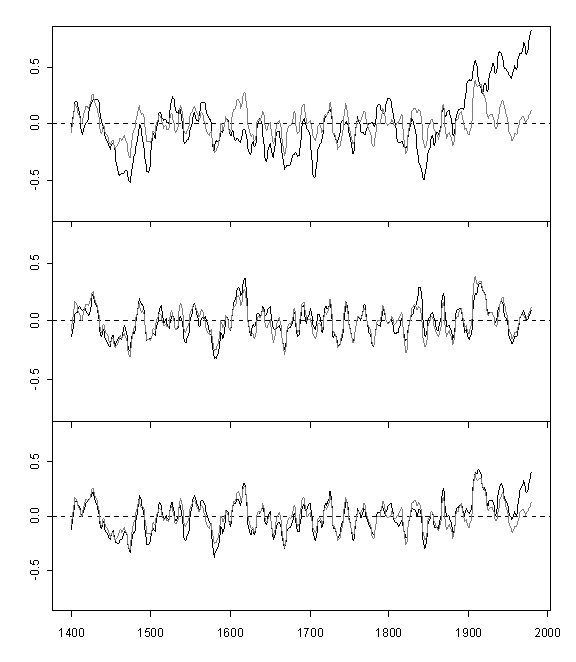
MM05d Supplementary Figure 1. Leading principal components calculated using three separate PC methods (black) and the all-series average (gray) of the North American tree ring chronologies: (a) the MBH98 normalization, (b) covariance matrix, and (c) correlation matrix. Contrary to Huybers, the covariance PC1 and the correlation PC1 are both similar to one another and to the all-series average through most of their history, while differing considerably from the MBH98 PC1. The all-series average and PC series have their variance (but not mean) adjusted to the instrumental record between 1902 and 1980. For visual clarity, all records are shown after smoothing by an 11 year gaussian filter.

I thought that Huybers raised an interesting issue on the RE question, although his use of terms like "REfix" was irritating. I enjoyed replying to this point and the exchange on this topic definitely added to the sum of knowledge on this little issue. But the principal components exchange seemed pretty pointless to me and marred by contentious language, which I fear is going to live on this debate.