Jean S has sent the following longer contribution on Rutherford et al 2005. I always appreciate Jean S’s thoughtful comments (which is no secret to readers here). So enjoy. JeanS:
Now since the review of Burger and Cubash [BC06 here after] put Rutherford (2005) [R05] back on the table, there is an issue to which I’d like to draw readers’ attention. This issue went completely unnoticed by the AR3 of BC06 [I wonder if AR3 was a reviewer for R05 also, if so, what were his/her comments]. IMO, the issue is not fully noticed by BC, either. Namely that R05 does not use the RegEM algorithm by Schneider(2001), but a modified version of it. In fact, there are at least three completely ad-hoc modifications introduced in R05, I’ll discuss them below in some detail.
As a general note, one should recognize that any (optimal) properties proved for RegEM can not be claimed for the R05 version, since it has not been shown anywhere that these (ad-hoc) modifications introduced do not change the properties.
1) “Hybrid frequency modification”
This step is “justified” in R05 with a lot of handwaving without any indication of its mathematical soundness. There are some RE values given for the reconstruction, but those values seem to differ little. So it is hard to understand why this step was needed given the the trouble in coding etc.
Modification introduced: instead of using RegEM directly on (proxy) data, R05 chooses to apply RegEM to separately to “low” and “high frequency” components. In essence, they filter the proxy data with a low pass filter (10 point Butterworth) to create the “low frequency” component and then take the residual as the “high frequency” component. Then each of these series is given “weight” which is essentially the ratio between their variances with respect to the variances of unfiltered series. Then this weight is used as an initial covariance estimate for the RegEM, which is applied separately for the both series. Finally the results are somehow combined.
The combination code is not provided in Rutherford’s web page (why not???) [As a side note: Rutherford’s code is terrible to read, and I would go nuts if any of our PhD-students would return me code like that not to speak of making it public.] and the combination is described in R05 as:
The REGEM method is applied separately to the calibration of proxy and instrumental data in the high- and low-frequency bands. The results of the two independent reconstructions are then recombined to yield a complete reconstruction. Each proxy record is weighted by a bandwidth retention factor defined as the percent of its total variance within the particular frequency band under consideration. For example, a proxy record dominated by interannual variability, with
very little low-frequency variability (e.g., a very data-adaptive standardized tree-ring record) would be assigned a high weight (near one) in the high-frequency band calibration and a low weight (near zero) in the low-frequency band calibration.
From which I couldn’t figure out the exact details. If anyone can help me with this, I would be grateful as this would allow the complete testing of Rutherford’s results.
At this point I’d like also to remind the readers about the AR3 (of the BC paper) comment:
Concepts are used loosely in a way that leaves their specific reference in the context unclear
Hmmm… isn’t that customary in the field 😉
Anyhow, it seems that the “low and high frequency” component results are somehow weighted with respect to the relative variances of the proxies (under what period?). In essence, this step gives, in BC terminology, yet-another-flavor introduced by the hockey team. This is somewhat recognized by BC as they state in their answer to AR2 (see also the nonsense answer by AR2):
Regarding the hybrid-20 variant, Rutherford et al., 2005 state: “As described below, cross-validation experiments motivate the choice f = 0.05 cpy (20-yr period) for the split frequency in almost all cases.” – This sentence illuminates how a posteriori selections penetrate a model definition. If there is no extra (independent, a priori) motivation for that choice, the chosen model is no longer independently verifiable. This is especially critical if the above cross-validation is sensitive to the parameter in question, and is of course dramatically aggravated with the number of such choices.
However, IMO BC have not fully realized the arbitrariness of this step. Not only there is the “cut-off-frequency” variable issue (as realized by BC above), but also the ad-hoc weighting is used as an initial estimate for the covariance matrix and, supposingly, is later used in combining the “low” and “high” frequency results. Potentially, I see another “Mannian PCA”-step that would give high weight for proxies with “right” properties. In any case, the arbitrariness of this “yet-another-flavor” should be IMO clearly stated in the main BC text.
I also find it curious that Mann goes nuts on the detrending/trending-issue, but here, without hesitation, he is ready to introduce this type of procedure which seems to allow any type of “detrending” one is looking for.
2) “Stepwise modification”
This is a modification that I think that have not been discussed much before.
This step was “justified” in R05 by an unreported toy example. I find it troubling that in “climate science” papers you are allowed to modify existing algorithms and then justify the modification by simply claiming that the modification “works better” in a single toy-example. It seems that one does not need to even provide the results of the toy-example runs for the reader to check. Even worse in R05, they modified a recently proposed algorithm that in itself has not been fully explored. Anyhow, the “justification” in R05 ends:
The stepwise approach performed as well as or better than the nonstepwise approach in cross validation in each of these experiments. The results of these pseudoproxy experiments give us some confidence that the primary conclusions presented in this study are insensitive to whether the stepwise or nonstepwise approach is used.
This is very troubling for at least three reasons: a) either the first sentence is not correct or this is a strong case for inappropriateness of the used metrics b) they generalize the results of single toy example c) if the results are truly insensitive, why then use a modification?
The idea in this modification is that instead of calculating the target (temperature field) by inputing the whole available data into the algorithm at once, one reconstructs the temperature field in a step-wise manner: first back to 1820, then back to 1800, and so forth. This method leads to different reconstruction as that implemented by BC06 (for the AD1400 step):
if we are at step AD1400, the temperature field for the period 1500-1855 is obtained from the step AD1500 so it is not calculated by RegEM as in the BC06 implementation. In other words, the AD1400 step have no effect to the temperature field past 1500.
Now, the Table~2 in R05 supposingly calculates the RE values with respect to the BC06-style implementation (using only the proxies available to the given time). However, BC obtained clearly lower value for the AD1400 step (from the reply to AR2):
For this setting they report a verification RE of 40% (66% for the “early” calibration, with even 71% for the “hybrid-20” variant), as opposed to our emulated RE of 30%..
BC give possible reasons for the difference:
a) different temperature data (NH only, newer CRU version), b) different calibration periods than MBH98 (1901-1971 and 1856-1928), and c) an infilling via RegEM of the incomplete temperature data set prior to the entire analysis.
These are good sources for the difference reported, but IMO the difference (0.1) seems just too large to be completely explained by those factors alone. Rutherford’s code does not show how Table~2 was calculated. So maybe, just maybe, instead of calculating Table~2 in BC06-manner, they used the following procedure:
a) calculate the temperature field backwards as usual (maybe NaNing the verification period at each step)
b) calculate the verification temperature field for the target period by NaNing the verification period
BUT using the rest of the temperature field obtained so far (instead of using NaNs for the whole non-caliberation temperature field). I think this is worth considering in some detail. Another possible source for the difference is the fact that there is “yet-another-flavor” introduced in R05:
3) Unreported “standardization”
There is a “standardization” step in Rutherford’s code, which seems to be (to my knowledge) unreported. Here’s a segment of the code (taken from “mbhstepwiselowrecon.m”, but the same is present in all reconstruction codes):
[nrows,ncols]=size(composite);
if i==1% first step standardize everything
means=nanmean(composite(500:560,:));
stdevs=nanstd(composite(500:560,:));
composite=composite-repmat(means,nrows,1);
composite=composite./repmat(stdevs,nrows,1);
save standardlow
else % now just standardize the new pcproxy network
means=nanmean(composite(500:560,1009:1008+nproxies));
stdevs=nanstd(composite(500:560,1009:1008+nproxies));
composite(:,1009:1008+nproxies)=composite(:,1009:1008+nproxies)-repmat(means,nrows,1);
composite(:,1009:1008+nproxies)=composite(:,1009:1008+nproxies)./repmat(stdevs,nrows,1);
end
The above code “standardizes” all proxies (and the surface temperature field) by subtracting the mean of the calibration period (1901-1971) and then divides by the std of the calibration period. I’m not sure whether this has any effect to the final results, but it is definitely also worth checking. If it does not have any effect, why would it be there?
References:
Rutherford, S., Mann, M.E., Osborn, T.J., Bradley, R.S., Briffa, K.R., Hughes, M.K., Jones, P.D., Proxy-based Northern Hemisphere Surface Temperature Reconstructions: Sensitivity to Methodology, Predictor Network, Target Season and Target Domain, Journal of Climate, 18, 2308-2329, 2005. Code and supplementary material available from: http://fox.rwu.edu/~rutherfo/supplements/jclim2003a/
Schneider, T., Analysis of incomplete climate data: Estimation of mean values and covariance matrices and imputation of missing values. Journal of Climate, 14, 853-871, 2001. Code available from: http://www.gps.caltech.edu/~tapio/imputation/index.html
Bürger,G., Cubasch, U., On the verification of climate reconstructions Climate of the Past Discussions, 2, 357-370, 2006




44 Comments
Thanks, Jean. And thanks to Rutherford for separating reality into low frequency and high frequency realities, with separate weights.
Now all we have to do is figure out if we are in a low or high frequency reality today, and then we will know whether to believe the data we are seeing.
So what do the statistical verification metrics like r2 or Durbin-Watson give as a result of this wondrous procedure?
Also it would be interesting what Dave Stockwell would produce using random numbers with LTP with this method.
#2 Yeah, who has the time for it though. R05 takes some pretty stern and uncalled for swipes at M&M too. I was thinking of a new way of doing reconstructions. Why not just weight the proxies by their correlation with local temperatures, then average them? e.g. multiply the proxies in a grid cell by the r2 value then average, then average equal area grid cells for the global mean.
Is this too obvious? This would be a simple automatic filtering process. Instead of filtering by variance and correlation with global temperatures. Do you know of anyone in the dendro literature who has done anything like this?
One of the particularly ironic things about R05 is that they collate instrumental and proxy data incorrectly – one year off, just after arguing that Mann et al didn’t do this – that the error only existed in the “wrong dta” – provided by none other than R. (Of course this collation prblem was only the beginning of the principal components problems.
# David. Look at my posts on the Linear Algebra of MBH. The MBH regression method ultimately weights proxies by their correlation to the the temperature PC1 (so it’s along the lines of what you propose). That’s equivalent to “Partial Least Squares” – a known method especially in chemometrics. Mann and Jones 2003 do something like this, but do not disclose their weights. Hegerl et al 2006 appear to have re-invented correlation weighting.
Think about what happens in OLS betwen standardized series. You calculate a vector of correlation coefficents which is rotated by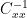 . If the series are close to orthogonal as in the 15th century network, then
. If the series are close to orthogonal as in the 15th century network, then 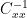 is close to the identity matrix and OLS results are close to PLS.
is close to the identity matrix and OLS results are close to PLS.
So the process ends up being similar to a multiple inverse linear regression of temperature on 22 proxies (e.g. Groveman and Landsberg).
If you have 12 proxies located here and there in the NH, how do you assign weights?
I think that one is better to require proxies that you know ex ante are up or down and therefore correlation systems (that permit flipping of series) are out.
Steve, I must confess I haven’t gone through it in detail. I assumed the PC1 was global, but you are saying it is local temperatures? Then if the temperatures in the grid cell for the bristlecones shows no correlation (don’t they), why do the bristlecones get weighted at all?
Because of the correlation with the global temperature index of the early twentieth century.
Yes but that is what I am saying shouldn’t happen. What if there were no fitting to global data at all. Series were just fit to the local grid cell temperatures, and weighted according to their correlation. Looking at Steve’s previous posts, the bristlecones/foxtails have an r2 of less than 0.1 with local temperatures, so their variance should be reduced to a tenth.
Re #8
But that is the point. The whole procedure weights according to correlation with the global temperature index not to local temps – that’s why the bristlecones are weighted so highly.
Bloomfield referred to this as an “honest attempt” to reconstruct past climate change, but to an amateur like me, it looks like either nobody understood what they were doing or they were fabricating a particular view of past climate based on greenhouse warming due to fossil fuel use.
Without being telepathic its impossible to tell which one it is.
#9 Well exactly. And isn’t this the underlying bogus assumption in all these methods — the influence of a global temperature field. If you just weighted them by local temperatures instead, apart from data limitations, the weighting would attempt to reduce the effect of proxies with non-temperature variance. That would be honest, to say they have variable amounts of temperature response, and that response is a local phenomenon. All methods with global fits however done have the ‘supernatural’ global temperature field influence.
I suggested this a while ago also. It is prone to issues with data mining, however, but still seems like a simple start. At the end of the day, you are doing some sort of comparison of proxies to instrument during the time that you have data and then reconstructing temps of the past from proxies of the past. A thermometer with more correlation in calibration ought to be more heavily weighted. To avoid the data mining issue, some calibration that shows good performance versus interannular effects is needed. Then weight based on “performance” (may not be a simple correlation).
The PC1 is global and has info left out of it. So weighting versus that seems very wrong. The global thing drives data mining and unphysicality. The having info left out seems eggregious as you are basically getting circular logic: the dominant mode of variance and all that.
10. That’s right. I can’t think of any way to scientifically justify correlating a series in California with some “global average temperature.” It’s preposterous!
#11. Sorry I must have missed that. No method is perfect but you can set up a series of most simple approaches. e.g.
level 0: average proxies
level 1: weight by local temp correlation and average
…
Then you have something simpler to study. The global PC1 idea has the fundamental assumption of global teleconnections for temperature. While on the surface it lookes OK if you just look at the mathemetics, surely this is an appeal to a ‘supernatural’ force behind tree growth. Hence, it is unscientific and unacceptable.
It’s especially ironic that the Mannian tribe ascribes the MWP to “localized” effects, and then goes on to correlate California tree rings to “global temperatures,” as if nothing is localized effects don’t exist.
I’ve posted a similar comment elsewhere, but can’t remember which thread. I’m growing increasingly concerned about many procedures used in palaeoclimate reconstruction. One of these is highlighted by the discussion you are having relating to proxies and supposed teleconnections to the global average temperature. Often there is no phenomenological description of why this should be so, and less a decent constitutive relationship between the proxy and temperature. This is particulalry so for tree rings.
I would like to see more fundamental research into proxy signals and local temperature. My view is that the oxygen isotopic composition of high latitude ice cores might be one good proxy where we understand the link between local temperature and isotopic composition. We also can back this up with the borehole temperature profiles. Of course these don’t show a significant modern warming and also record the LIA and MWP. Other good proxies might be palaeoprecipitation as recorded in speleothem fluid inclusions and groundwater. There are problems with these proxies but they are promising and offer a multi-technique approach. For example groundwater recharge temperatures can be estimated using both stable isotopes and noble gas mixing ratios. Steve has pointed out to me that using dendrochronology and tree lines is another way to try and estimate robust local temperatures.
If we can use such proxies then I believe we can start to make robust estimates of past climatic means etc.
I’m not a statistician and so the next comment might be idiotic, but here goes. If a PCA is done with a tree ring data set is not one of the problems that the components are not truly orthogonal, i.e. independent. One can imagine that parameters such as moisture availability, temperature, precipitation all covary to an extent.
I found this comment on a Jean S post by Paul Dennis (of UEA?) and the ensuing discussion to be of much interest. It does not seem like much attention is paid yet to rigorous understanding of the physical basis behind the statistical games of The Team??
15.
I’m not a statistician, either, but you are right on target, I think. You don’t have to have a PhD in statistics to understand how hard it is to deal statistically with the number of variables involved in tree growth. And I don’t think any statistical manuevering, like detrending, smoothing, RCS, etc. can isolate the effects of temperature, which are probably greatly overshadowed for most trees by moisture and other factors. Hell, growth does not even vary linearly with temperature (it increases with temperature from about 5 degrees to 20 degrees, levels off for a few degrees, and then DECREASES with higher temperatures). Most of the variation in tree growth in old trees can usually be explained by precipitation, and tree rings can be very good for studying droughts.
Or a VERY extensive root system!
I read Rutherford 2005 in more detail and it actually does compare a climate field approach with local calibration. The justification for climate field is a classic:
as though its a good thing.
If you think that, say, spruce ring widths are a proxy for temperature, then I don’t think that it’s reasonable to say that some spruce correlate better with gridcell temperature than others. I think that you have to take them all.
In the tree ring world, I think that the various bias issues ("modern sample bias", "pith offset bias", altitude bias, cherrypicking) are all bigger issues than the precise form of multivatiate methods. Again all you’re doing in a multivariate method is taking a weighted average of series. In situations where there’s an actual signal, the precise method doesn’t seem to matter very much. But in situations where it’s a dog’s breakfast, you get very different results depending on what’s chosen.
I would place more stress on really getting a good history from a few sites and less effort on trying to winkle out results from a grab-bag of data.
Re: #19: You’re much more generous to the Hockey Team and their curiously inept attempts at dendrochronology than I am Steve. I think that I would tell them to go away and do the job properly, and when they have it figured out, to come back and tell us the answer.
But by the way, you had better find some proxies for temperature where you can prove a linear relationship that is consistent with the data for different periods, and different locations. Oh, and why don’t you check with the stats department at your local university, and ensure that you are using accepted methodology.
And when you are done, if you want to restore your cred, you had better document your results with well written papers that detail your methods, explain why you have used them, and present the data that demonstrates your point in such a way that others can replicate your work, and so endorse it.
Of course, it would be useful to have a look at the published temperature series showing increases in the “Global Mean Temperature” over the past century too. I think that if you can persuade the guardians of the data to release their data and methods as to how they came up with the series showing global warming, you might find some interesting insights. You may well find for example that actually the supposed rises in “Global Mean Temperature” are not really there if UHI effects and other station sampling biases are excluded.
And wouldn’t it be ironic if the outcome was that dendrochronology studies showing not much warming are matched with temperature series that show not much warming, thereby showing that dendrochronology works after all!
JEan S, I have two previous posts on Rutherford et al 2005 at http://www.climateaudit.org/?p=513 and http://www.climateaudit.org/?p=519.
#20 Nicely put! On the other hand, having tried to apply PCA and other multivariate methods in the past (mostly to small-dimensional hydrological datasets), I am doubtful that PCA can ever deliver in practice what it promises in theory. PCA is too sensitive to the sorts of problematic characteristics that proxy climate data exhibit: outliers, data errors, confounding factors, and non-standard distributional shapes.
Of course, if you torture data long enough they confess to just about anything (including, as Steve has shown, hockey sticks).
re #1: John H, additionally you must realize that the temperature field is not filtered only proxies are. So we are supposed to divide proxies into low and high frequency realities, but, of course, not the instrumental temperature measurements. That would be a stupid thing to do ;). Hmmm, on the other hand, MBH98 proxy network contains some temperature series… Oh well … 🙂
This is one of the things that is the most irritating about the hockey team work. They have a tendency to show a single anecdotal case and then subsequently refer to this as some sort of “proof” of a statistical method. This kind of thing is popular in political debates but has no place in science. (Except possibly in pathological science)
re #19:
Indeed. One of the most suprising things to me so far on my little journey to the climate science is that, contrary what it first appears, there actually is some good science done in the reconstructions field but it seems to be hidden to smaller circulation journals. Only certain guys are publishing in Nature etc. I would not be even suprised if we already have many enough “good histories” to actually try to make a reasonable, quantitative NH temperature reconstruction for the past millenium. As an example of IMHO a well done local temperature history is the recent article I gave the reference earlier:
J. Weckstràƒ, A. Korhola, P. Eràƒ⣳tàƒⴠand L. Holmstràƒ, Temperature patterns over the past eight centuries in Northern Fennoscandia inferred from sedimentary diatoms, Quaternary Research, Volume 66, Issue 1, pp. 78-86, July 2006. http://dx.doi.org/10.1016/j.yqres.2006.01.005
BTW, Eràƒ⣳tàƒⴧs recent PhD thesis (applied mathematics) is available from here. It may be worth to check it out even if one (like me) is not so interested in Bayesian statistics.
Jean S, have you tried to run mbhstepwiselowrecon.m and mbhstepwisehighrecon.m? I tried and had to fix a few problems in order to get the scripts to run. Not sure that I have found all the problems. Another problem is that the instrumental gridcell temperatures that are supposed to be contained in annualrespliced.mat are garbage.
25. Yes, there ARE some good studies out there (none of which use tree rings); and all that I’ve seen clearly show the LIA and MWP.
#26. Phil, what’s the nature of the problem with the gridcell temperatures?
Steve, the data just doesn’t look like temperatures i.e. for gridcell 4 the first 4 entries are 0.7875 -134.4861 -98.5328 33.0166 where the entries corresponded (if I have interpreted the comments correctly) to 1856 1857 1858 1859. The rest of the gridcell entries also lack any resemblance to temperatures. I can email you an ascii text file of the matrix or perhaps just a portion of it. The only possible legitimate reason is that Rutherford is using an early version of Matlab, and that Mathworks has changed the file format on their *.mat files. Normally, Mathworks is good about backwards compatibility or at least gives an error message. Coldrespliced.mat and warmrespliced.mat are also bad.
Assuming each row is an observation and each column is a station, I agree with Phil B. The data are all over the map when loaded into version 7 (release 14, service pack 3).
Mark
Phil – I wonder if this relates to the splicing problem noted here http://www.climateaudit.org/?p=519 . It looks to me like most of the entries are temperature*100, which you often see in these datasets. It;s the first entry that might be the odd duck and that might be a collation problem.
Thanks Steve, I divided by 100 and the gridcells plots look more like temperature anamolies. What the motivation/origin for the *100?? I averaged the cells and got the classic 0.6 C delta plot for the last century.
I agree again.
BTW, how representative is this series of the actual planet? I.e. there seems to be no geographical weighting.
Mark
RE 25:
CO2science has a summary of regional proxy studies, tho I don’t know how much they’ve been “cherry-picked”:
http://www.co2science.org/scripts/CO2ScienceB2C/data/mwp/mwpp.jsp
I’ll look more cerefully the intrumental temperature issue today, there seems to be somewhat interesting things 🙂 I already noticed (see the code script in the post) that I made a mistake: the standardization period is in fact 1899-1959!!! I suppose that here is another (see Steve’s earlier post) off-by-one (or two) error (they wanted to have something like 1901-1960), but still, why the last years are not used? Their caliberation period is supposed to be 1901-1971.
RE #32 Phil B,
“What the motivation/origin for the *100??”
The numbers are monthly averages of daily numbers of however many stations are used for that grid cell, rounded to hundredths.
Furher to my previous answer, by using units of 0.01 C, instead of 1 C with a fraction of two digits, the need for a decimal point is avoided.
Is anyone else bothered by this “Global Climate Field” concept? It just seems that something as ill-defined as this is inviting abuse.
Also some practices are carry-overs from Fortran programming.
#38, Paul
Bears are not toilet-trained.
Thanks, JerryB for the info.
Pielke Sr’s site has posted some comments on possible arctic ocean ice-free conditions during the Holecene max (only ~10000 ya) & Canadian arctic tree-line movement (more examples of older, neglected studies that don’t fit the “consensus”):
http://climatesci.atmos.colostate.edu/2006/07/12/open-arctic-ocean-commentary-by-harvey-nichols-professor-of-biology/
Is it just me or does this thing (mbhstepwiselowrecon) take FOREVER to run?
Mark
2 Trackbacks
[…] self-contained and so I re-visited some of our previous comments on Rutherford et al here here here here . I’m going to reprise two issues today: Collation Errors, a small but amusing defect; and […]
[…] July 10, 2006, Jean S commented on Rutherford-Mann 2005 “adaptations”, noting three important “adaptations: 1. use […]