The new Santer et al. paper, Forced and unforced ocean temperature changes in Atlantic and Pacific tropical cyclogenesis regions, purports to show that sea surface temperature (SST) changes in the Pacific Cyclogenesis Region (PCR) and the Atlantic Cyclogenesis Region are caused by anthopogenic global warming (AGW). They claim to do this by showing that models can’t reproduce the warming unless they include AGW forcings. In no particular order, here are some of the problems with that analysis.
1) The models are "tuned" to reproduce the historical climate. By tuned, I mean that they have a variety of parameters that can be adjusted to vary the output until it matches the historical trend. Once you have done that tuning, however, it proves nothing to show that you cannot reproduce the trend when you remove some of the forcings. If you have a model with certain forcings, and you have tuned the model to recreate a trend, of course it cannot reproduce the trend when you remove some of the forcings … but that only tells us something about the model. It shows nothing about the real world. This problem, in itself, is enough to disqualify the entire study.
2) The second problem is that the models do a very poor job of reproducing anything but the trends. Not that they’re all that hot at reproducing the trends, but what about things like the mean (average) and the standard deviation? If they can’t reproduce those, then why should we believe their trend figures? After all, the raw data, and it’s associated statistics, are what the trend is built on.
Fortunately, they have reported the mean and standard deviation data. Unfortunately, they have not put 95% confidence intervals or trend lines on the data … so I have remedied that oversight. Here are their results:
(Original Caption) Fig. 4. Comparison of basic statistical properties of simulated and observed SSTs in the ACR and PCR. Results are for climatological annual means (A), temporal standard deviations of unfiltered (B) and filtered C) anomaly data, and least-squares linear trends over 1900–1999 (D). For each statistic, ACR and PCR results are displayed in the form of scatter plots. Model results are individual 20CEN realizations and are partitioned into V and No-V models (colored circles and triangles, respectively). Observations are from ERSST and HadISST. All calculations involve monthly mean, spatially averaged anomaly data for the period January 1900 through December 1999. For anomaly definition and sources of data, refer to Fig. 1. The dashed horizontal and vertical lines in A–C are at the locations of the ERSST and HadISST values, and they facilitate visual comparison of the modeled and observed results. The black crosses centered on the observed trends in D are the 2 sigma trend confidence intervals, adjusted for temporal autocorrelation effects (see Supporting Text). The dashed lines in D denote the upper and lower limits of these confidence intervals. I only show Figs. 4A and 4B. The left box is Fig. 4A, and the right box is 4B
I have added the red squares around the HadISST mean and standard deviation, along with the trend lines and expected trend lines. Regarding Fig. 4A, which shows the mean temperatures of the models and observations, the majority of the models show cooler SSTs than the observations. Out of the 59 model runs shown, only three of them are warmer in both regions. Two of them are over two degrees colder in both regions, which in the tropical ocean is a huge temperature difference. Only one of the 59 model runs is within the 95% confidence interval of the mean.
Next, look at the trend lines in 4A. In the real world, when the Atlantic warms up by one degree, the Pacific only warms by about a third of a degree. Even if the mean temperatures are incorrect, we would expect the models to reproduce this behaviour. The trend line of the models does not show this relationship.
The standard deviations (Fig. 4B) are even worse. There are no model results anywhere close to the observations. The majority of the models tend to overestimate the variability in the Pacific, and underestimate the variability in the Atlantic. This is probably because the variability is inherently larger in the Atlantic (standard deviation 0.35°), and lower in the Pacific (standard deviation 0.24). However, this difference is not captured by the models. The trend line (thick black line) shows that on average, the model Pacific variability is 90% of the Atlantic variability, when it should be only 60%. The light dotted line shows where we would expect the model results to be clustered, if they captured this difference in variability. Only a few of the models are close to this line.
3) All of this begs the question of whether we can use standard statistical procedures on this data. All of the data is strongly autocorrelated (Pacific, lag(1) autocorrelation = 0.80, Atlantic = 0.89). In their caption to Fig. 4 they say that they are adjusting for autocorrelation in the trend sigma. Unfortunately, they have not done the same regarding the standard deviations shown in Fig. 4B.
In addition to being autocorrelated, the Pacific data is strongly non-normal (Jarque-Bera test, p = 
As you can see, the data is quite skewed and peaked. Thus, even when we adjust for autocorrelation, it is unclear how much we can trust the standard statistical methods with this data.
4) There are likely more problems with this paper … but this is just a first analysis.
My conclusion? These models are not ready for prime time. They are unable to reproduce the means, the standard deviations, or the relationship between the two ocean regions. I do not think that we can conclude anything from this study, other than that the models need lots of work.
w.
Climate Audit 
35 Comments
It seems to me that all the models are prime examples of overfitting. But they can’t even show the MWP and LIA, so they are lousy jobs of overfitting. The overfitting studies I like show a healthy MWP and LIA, but Bender keeps lowering my ClimateAudit grade, because I like those studies. I’m in a quandry.
In order to be a climate modeler, you must believe that there is a manageable number of variables that are the most significant elements in climate change. By the looks of all of the different charts, models, errors, and just plain different answers, things are not simple enough or have not been defined well enough. In the aircraft business there is a reasonable number of variables that together cause 99% of the flight result. Because there are a relatively small number of significant variables, the impact of change of each variable has been studied in depth and is well understood. Models are developed that address this limited number of variables and the result is that contemporary aircraft models end up behaving extremely close to the real aircraft performance.
Unfortunately it appears global climate does not provide this same small number of significant variables, nor is the modeling of them appear to be replicable in straight forward formulas. Otherwise we would probably have some successful ones by now. If one is to develop a useful model I believe they need to do the following:
a) Identify all significant variables that can impact global climate
b) Identify how much each variable impacts the climate, how it interacts with the other variables, and come up with iron clad justification on that quantification
c) Develop the model
If you can’t do a quality job on a) and b) – you cannot do c).
Unless there are perhaps only 3 variables, then maybe you can by accident. I suspect we are talking about massive numbers of variables though, but that is just my humble opinion.
Since there is claimed consensus on AGW in the scientific community, and it all apparently comes from the climate models, then there should be consensus on a) and b). If there is I would like to see it. If not, then obviously it would be useful for the world to have an accurate climate model, if that is indeed possible. Through extensive debate on this blog I have seen some consensus on variables and their impacts come out of unlike minded people. Can the unruly crowd in this blog come to a consensus on a) and b)? I suggest that if you are so inclined to take up the challenge, tackle a) first, as that will engender enough debate on its own.
On another thread, Pat Frank commented:
Actually, I haven’t a clue what Santer knows or doesn’t know. I am continually amazed by the claims made by the modelers and their friends regarding the models. Everyone seems to think that the models are based on physical principles, which they are not. They are a collection of forcings associated with parameters that are very carefully tuned to match, not the mean, not the standard deviation, but the trend.
Despite that, they all seem to think that if they pull out one forcing and the model no longer predicts a single number, the trend, that this “proves” something. Me, I think all it proves are that the models are tuned to certain parameters and forcings, and they won’t work without all of them
They showed the differences in the mean and standard deviation in their study, but their comments on them are curious:
Most of them underestimate the mean (report too cold a temperature), and that’s their only comment? Just to note that it’s happening? What are the implications of this?
And why are these variance differences not statistically significant? They do not give any indication of the confidence intervals on the standard deviations, but they are easy to estimate. The standard error of the standard deviation is
. N is the number of observations, which are monthly for 100 years, or 1200. With that information, you can tell me if the differences are statistically significant.
Here’s another comment, this one on the low-frequency standard deviation results:
Let’s parse this. The individual model runs have great within-model variability regarding low frequency variability (low frequency standard deviations are large). What would my conclusion from this be? It would be that the models are internally unstable at low frequencies.
But what do they conclude from this? Their conclusions are:
In other words,
1) The models are fine, but
2) We need a larger model ensemble to get good data, and
3) It may be hard to get good low-frequency data from the observational data.
Would that be your conclusion? That the model results are scattered all over the place, and few of them give results anywhere near the observations, so we need more models?
This is like Santer’s earlier paper, in which, when the models disagreed with the observations, said it was more probable that the observations were wrong …
How did the reviewers miss these points? I don’t know, but I guess it’s easy, if you are a true believer. For true believers, the only thing that matters is the conclusion. If the conclusion fits their preconceptions, they don’t look at it very hard.
I don’t know if they know that the Pacific results are non-normal are not. The know they are autocorrelated, but they ignore that very relevant fact when looking at the standard deviations … how do I know what they know, and what they are just ignoring?
My analysis took about 6-8 hours, because I had to collect the SST data, and then figure out what they had done to get their results. Will I write it up? Don’t know, I’ve done it before with no results, and am not fond of tilting at windmills. If all of the people involved believe that the models are worthwhile, valuable, and accurate (as they obviously do), will my writing change anything?
w.
#3 — Thanks, Willis, I admit to being a little stunned. I guess the question would better have been couched, ‘Should Santer have known,’ rather than ‘did he know.’ But then, the answer to the revised question is obvious.
I’m reminded again of pathological science, “These are cases where there is no dishonesty involved, but where people are tricked into false results by the lack of understanding about what human beings can do to themselves in the way of being led astray by subjective effects, wishful thinking, or threshold interactions.” Although there also seems to be a quasi-junk science element (paraphrasing), “[inadvertantly] sloppy research usually conducted to advance some extrascientific agenda or to prevail in litigation.”
I wish you would write up a scientific criticism, Willis. But perhaps ‘cc’ it at the bottom to a few newspaper editors. The climate field is besotted with publicity. Maybe the journal editor will pay attention to your analysis if s/he knew that newspaper editors were in the loop.
Next time anybody has a chance to discuss AGW with a journalist, ask them why “flux adjustments” are necessary if the science is settled. Ask them why the IPCC’s predicted warming ranges from 1.5C to 4.5C – not exactly a narrow range – if the science is settled. Ask them why there are so many GCM’s if the science is settled.
As them why they think the science is settled.
Actually Kevin, flux adjustments are not used in the latest generation of models. As to why there are so many GCM’s: there are lots of approaches to modeling the climate, none of them optimal. The science of climate modelling is far from settled. This does not mean however, that the science of AGW is *not* settled. The basic physics of the effect of CO2 on the climate are well understood and the question of detection has been answered to the satisfaction of most climate scientists. The open question is one of sensitivity, and even that seems to be coming down to the figure of 3.25 +- 1.25C if one assumes that there is not a tipping point and refuses to give in to one’s deepest fears…
#6 — So, JMS, what are the 95% confidence limits about a centenary climate projection, in W/m^2, of your favorite GCM when the parameter uncertainties are propagated through the calculation?
If the science is settled, the basic physics are known, and the attribution is sure, then surely the widths of the confidence bounds are smaller than the forcing that is being modeled. Aren’t they. So, what are they?
Willis,
Unfortunately I’m pressed for time but did Santer et al consider Pallé et al 2006 (EOS Vol. 87, No 4, pp, 37,43, January 24?
I would think that the increased insolation due to decreased albedo (less clouds) of the last decades until about 1998-2000 could have been more than enough cause for increasing SST.
Off track, but note also that Pallé et al are flat wrong. Temperatures did not continue to increase when the albedo started to increase again. In fact the r2 of albedo with giss temp is some 58%, showing that we don’t need any anthropogenic factor to explain the current warming.
JMS, the information I have regarding flux adjustment, from insiders and very recent, is that they are indeed still used and in fact that this is no longer regarded as contoversial. (At one time this practice evidently was strongly debated within the Climate Science community.) One of the parameters that is adjusted is the key one – climate sensitivity, as you yourself note.
I could say more however it is sufficient to reiterate the wide range of CLAIMED uncertainty should caution one against uncritically accepting the claim that the science of AGW is settled.
JMS, thank you for your contribution. While it is true that atmosphere-ocean flux adjustments are not used in the latest generation of models, perhaps you could comment on the number of adjustable parameters and assumed values that are present in the latest generation of models.
The truth is that there are a number of parameters that allow them to tune the models. Unfortunately, when they tune the models to reproduce one aspect (trend), many other aspects get out of whack.
According to the modelers 2006 analysis of their own model, the GISS climate model (which does a good job of reproducing the historical trend, and which claim an error of only 0.3°C in hindcasting the SAT), has these differences from actual observations in their results (all numbers in w/m2):
TOA Solar Forcing__________1.5
TOA_absorbed SW__________2.2
TOA_outgoing_LW_________-6.9
TOA_SW_cloud_forcing_____2.8
TOA_LW_cloud_forcing_______10
Surface_absorbed_SW_____-4.2
Surface_net_LW__________-9.3
They’re nine watts/square metre short at the surface, ten watts long at the cloud long wave, seven watts short at the total outgoing long wave, and so on. Now remember that these folks claim that in their models, a doubling of CO2 leads to a 3.7 w/m2 increase in downwelling long wave, which they claim will give a 2.6° change in the climate. So let me recalculate their figures using their climate sensitivity, to get a sense of the size of these errors within their model:
TOA Solar Forcing________1.1°C
TOA_absorbed SW__________1.5°C
TOA_outgoing_LW_________-4.8°C
TOA_SW_cloud_forcing_____2.0°C
TOA_LW_coud_forcing______7.0°C
Surface_absorbed_SW_____-3.0°C
Surface_net_LW__________-6.5°C
(In addition, their cloud cover is low by about 10% … which you would think would make a huge difference in the albedo, but doesn’t … because the albedo is a separate parameter which is tuned to match the ERBE data)
Now, given the huge size of these errors … how do they get the trend right? How do they get the SAT within 0.3°C?
Parameters, my friend … tuning the parameters …
w.
Willis, a small point, but from my experience the probability distribution of SST is about as good as it gets for data to approximate a normal distribution, especially with such a small number of events. I suggest that you replot the data as a true histogram, i.e., as a stairstep function and add error bars. Each bin of the histogram is its own independent Poisson process, hence the one sigma error on the bin height is +/- sqrt(bin height). Let’s see how it compares to a normal distribution when replotted with errors.
RE #10: The GISS hindcast should have been a wake-up call to people who think the GCMs can forecast the future. They got the right answer using information that would have been unknown and unknowable to to someone at the start of the forecast period. Without those inputs the model would have gone wildly off the tracks. There’s also the issue of getting the global temperature right but the regional temperatures wrong. That’s just outright unphysical since the global temperature is a mathematical composite of the regional measurements. Alligators at the poles, polar bears at the equator, but we get the right global average!
#6 – JMS, if the science is settled as you say, can you explain why the empirical climate sensitivity is a mere 0.22 C/W/m2 or around 0.8 C per CO2x2 ? I have never seen any climate scientist try to address this, and that is sort of worrying.
As I have found typical with your comments Willis, I learn a great deal from them. Given another 100 years or so I should get a handle on understanding this climate thing.
What is a flux adjustment? If it is a calculation used to estimate the transition of heat from one area to another I would say that the GISS models use them extensively. At least that is my impression from reading the GISS GCM Model E model description and reference manual listed at: http://www.giss.nasa.gov/tools/modelE/modelE.html#part3_4
I imagine that those flux calculations can play a huge impact in the result. Is there consensus on what those calculations are? Also, I am struck by the way the model description talks about plug and play elements of the model. I have no doubt that you can use these plug and play options and tune a warming, neutral, or cooling result as you see fit.
#10 — Willis, it looks like you’ve provided one answer for my perennial question.
#13. Some climate models go off the rails without artificial adjustments of energy – “flux adjustment”. Most of the IPCC TAR models required such adjustments to avoid spiralling out of control. The more recent models (ncluding a couple of TAR models) say that they no longer require flux adjustment and this was viewed as an important accomplishment within the community.
Re 13, 15, a flux, of course, is a flow of energy, or pressure, or other variable. The most common place for “flux adjustments” is in “coupled” climate models, where there are two (or more) climate models, with the output of one flowing over the interface to form the input of the other, and vice versa. Often this process simply doesn’t work “¢’¬? the models go off the rails. Some of the newest models don’t use flux adjustments, but the GISS model, being older, still does.
Rather than figure out what’s wrong with one, the other, or both models, it’s much simpler to use a “flux adjustment”, some function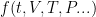
of time, volume, temperature, pressure, and whatever other variables you are transferring that adjusts these variables so that the two models don’t spiral into oblivion.
Now, what do they adjust them to? After all, there are an infinity of functions to do the transfer. Well, they adjust them so that the numbers coming out of the flux adjustment function give combined model results that agree with the observed temperature trend. One side effect of this process, of course, is that although the trend matches, other variables are way off (see #10 above).
Although the term “flux adjustment” is usually used to refer to adjustments between say an atmospheric and an oceanic model, the same process is used internally in each model. In this case, the adjustments are called “parameters”. In the description of the GISS model cited above, Schmidt et al. say:
In addition to what this says about parameters, this is an amazing admission about model resolution. Why should the results get worse as resolution increases? It indicates some fundamental problem with the model, because if the model is working properly, results should improve with increasing resolution, not get worse. Why not fix that, instead of … but I digress …
Parameters are discussed no less than 36 times in the document. They are mentioned as being applied to gravity waves, aerosol mixing, Rayleigh friction, thermal scattering, cloud optical depth, cloud asymetry, cloud single scattering albedo, prognostic cloud optical parameters, melt pond extent, cumulus and stratiform cloud formation, water droplet sublimation, temperature flows, moisture flows, scalar flows, pressure-velocity correlations, pressure-temperature correlations, conductance, ice mass flow, ice heat flow, saline ice mass flow, saline ice heat flow, surface fluxes, albedo, penetrating solar radiation, and non-local turbulent mixing … and those are just the parameters that are of interesting enough, or have changed enough, to mention in their report.
Now, we know that their model has at least 26 parameters, and likely more. Is this a lot? Is this a problem? Here’s Enrico Fermi on the subject:
w.
Well, my excursion into LaTex failed again … I wanted to say f(t,T,P,V …), which worked fine on my machine, but gave garbage on theirs. Let me try again. I’ll try f(t,V,T,P {…})
w.
Well, no joy. What I meant was:
w.
Willis, of course the latest version of the model, the being used in the current CMIP runs, does not use flux adjustments. I’ll reply to the rest of your message later, since it is dinner time.
Re 11, Paul, thank you for the valuable suggestion on the histogram. You say:
Don’t know what you call a “small number of events”. In this dataset (monthly values, 1906-2005), N = 1200. Here’s the results of a couple of normality tests for the data:
Jarque Bera Test (R function jarque.bera.Test)
data: PCR temperature, detrended, with monthly anomalies removed
X-squared = 60.5801, df = 2, p-value = 7.006e-14
Shapiro-Wilk normality test (R function shapiro.test)
data: PCR temperature, detrended, with monthly anomalies removed
W = 0.9867, p-value = 3.605e-12
In other words, both tests indicate that the data is extremely non-normal.
However, the test you propose (histogram with error bars) looks like this:
Who ya gonna believe?
w.
Re 19, JMS, thanks for the info on the latest GISS model. I look forward to your further post after dinner.
w.
#20: Willis
…me or your lying eyes?
The data with the error bars. (BTW, the normal distribution doesn’t have error bars, it’s an exact function.)
Are you plotting +/- 2 sigma? If the left hand axis is really counts the error on the 0.0 bin should be +/- 12 for 1 sigma.
Coming from the engineering world I would expect a GCM would work this way. You would develop a comprehensive thermodynamic model of the system, quantify all energy inputs and sinks and code this into a model. Then you would seed the model with initial boundary conditions, the climate status at Jan 1, 1900 for example, and then run the model.
If your assumptions are correct then the model would duplicate, within specified boundaries, the historical record. If it doesn’t you don’t understand the system and need to go back to the drawing board.
But this doesn’t seem to be the case, why not?
#22, #20, #11: Clearly the errors qualify as “extremely non-normal” if you consider statistical significance (p=10^{-Big Integer}). No surprise — when you have that much real data (is it real?), you invariably see extremely small p-values (i.e. high statistical significance).
However, like Paul Linsay, I am not sure significance is the right thing to consider. Perhaps a better question is whether the deviation from normality is substantial. To quantify this thought, how far do the sample skew and kurtosis actually deviate from 0 and 3, respectively? Also, is there some reason to think the conclusions might be sensitive to such deviations? (Just asking; I don’t know the answer).
The autocorrelation, OTOH, seems like a much more serious problem.
#20: Willis, sorry I got called away. To continue, the number of events needed depends on how small you want the error bars. With N=1200 the highest bins at the center have 10% errors and the bins in the tails have 100% errors. With 10,000 events you’ll reduce the errors by sqrt(10), etc. The plots you did for the hurricane counts only had 100 events with at best 30% error on the central bins.
Regarding your statistical tests, I don’t know what to say since I’ve never used them. I would do a least squares fit and see how good it is. By eye, it should be quite good.
#23. Agesilaus, have you read the recent CCSP report on reconciling surface and tropospheric trends. Observations show that the tropospheric trend is less than at surface, while all the models (and about 41 were examined) produced output under which tropospheric trends exceeded surface trends. The committee concluded that the observations were likely to be wrong and issued press releases that everything was reconciled. This feeds right into the S&C vs Wentz-Mears war, which makes matters Hockey Team seem pretty mild.
Re #26 the radiosondes will be under attack again, I imagine. While there is controversy about the accuracy of radiosonde-derived temperatures, to my knowledge their wator vapor (specific humidity) measures are OK.
Here is a plot of USNCEP reanalysis data for the global 300mb level (a height which approaches the top of the troposphere). The data is specific humidity. The trend is downwards. This downward trend is even more pronounced at adjacent atmospheric levels (see here for 400mb level).
I wonder if the models match this reality. One can argue about temperature, but a humidity record should be non-controversial. Do the models show a downward trend in upper-tropospheric humidity over the last 50 years? Do the models show events like the large rise seen at 300mb about 1976-77? (That 1976-77 event, by the way, whatever it was, shows up in a number of places and ways in the historical balloon data.)
Re #23: I couln’t agree more. Then again, I have also what would probably be considered a engineering background when formal training is concerned. In the Netherlands, where I’m from, engineers seem to be quite a significant part of the climate sceptics anyway.
And of course, any model that is tuned in the first place, does not prove causation in any way. A model that is only fed first principles and initial state can (in principle) do that by first checking if it does simulate climate for a give time frame, using known forcings etc, and then removing forcings for a different time frame and seeing which forcing combination is necessary and sufficient.
Then again, unless some serious change in attitude comes about in modeling circles, the current models will continue to be “improved” (i.e. made more complex and less transparent) and results will continue to be cited as proof of AGW even though they only prove that models are insufficiently accurate to give any clues let alone proof.
re#27 David, the radiosonde humidity measurements are MUCH worse than the temperature measurements, and hence we don’t really have anything reliable against which to check the satellite humidity measurements. Hence people don’t even try to do trends or anything with the humidity measurements
#16 Willis, you say:
“In addition to what this says about parameters, this is an amazing admission about model resolution. Why should the results get worse as resolution increases? It indicates some fundamental problem with the model, because if the model is working properly, results should improve with increasing resolution, not get worse. Why not fix that, instead of … but I digress …”
A possible reason (not looked at specific model) could be the loss of statistical significance at increased resolution (see Brown motion?)? Then certain generalization would have to be transformed.
It is nice that you brought us these nice Fermi words.
D.
Re: #11
Willis E, I see your points on the weakness of the case being made for the climate modelling calculations in this case, but the curve that you showed for the PCR SST distribution (versus the normal distribution) would appear to me from past experiences as capable of passing a statistical test for a normal distribution. Perhaps I am more accustomed to looking at curves with fewer data points and that is what is confusing me.
I am more familiar with a chi squared (goodness of fit) test of the binned distribution compared to that for a nomal distribution and/or something like a Jarque-Bera test based on the sample kurtosis and skewness. For my personal edification can you determine how the curve in question performs with these tests or why these tests are not applicable here.
PS Your graphs and figures have been very readable and much appreciated here.
For anova, regression etc. normality of residuals is not nearly as important as independence of observations & homogeneity of variance. The level of non-normality shown in these graphs is so slight that it is not likely to overturn a hypothesis test.
Just put in run order as a variable. Learned that in six sigma class.
# 30, Dmitri, thank you for your kind words. You also say:
Their cell size is large, tens of kilometres on a side or so, and so they are a long way from Brownian movement. I don’t understand the problem with increasing resolution at all.
w.
Re $ 19, JMS, you said that you were going to reply to my other points, and I was hoping that you would …
Thanks,
w.
One Trackback
[…] Willis on Santer et al 2006 :: Analysis of the Santer 2006 paper on tropical propospheric amplification. Tropical Tropospheric Amplification – an invitation to review this new paper :: New method used to examine the tropical tropospheric amplification. […]