I’m finally stating to come up for air after dealing with the fetid grubs and maggots of Hansen’s code. Needless to say, key steps are not mentioned in the underlying publications, Hansen et al 1999, 2001. I’m not going to discuss these issues today. Instead, I want to show 3 case studies where I’ve been successful in replicating the Hansen adjustment. In the more than 20 years since Hansen and Lebedeff 1987 and the nearly 10 years since Hansen et al 1999, to my knowledge, no third party has ever examined Hansen’s adjustments to see if they make any sense in individual cases. Some of the adjustments are breathtakingly bizarre. Hansen says that he doesn’t “joust with jesters”. I guess he wants center stage all to himself for his own juggling act.
I’m going to examine 3 stations today, which are the only 3 stations that I’ve examined so far. So these have not been chosen as particularly grotesque examples. The first two stations, Wellington NZ and Batticoala were chosen because they only had a few neighbors, a tactic that I used in order to try to figure out what the zips, bops and whirrs of GISTEMP actually did. The third station, Changsha, is the 1000th station in the GISTEMP station inventory.
After I do this, I’ll show how you can easily do similar plots for any station that you fancy, using materials and scripts that I’ve placed online. I have no idea how the emulation will hold up in other cases – I expect that there are more zips, bops and whirrs and adaptations will be needed – so let me know. Nonetheless, I’ve obviously broken the back of this particularly step. Going from here to gridded temperatures and hemispheric averages looks like a breeze in comparison, as Hansen uses a similar reference style in gridding and I can probably make simple adaptations of the hansenref program to do this.
Wellington NZ
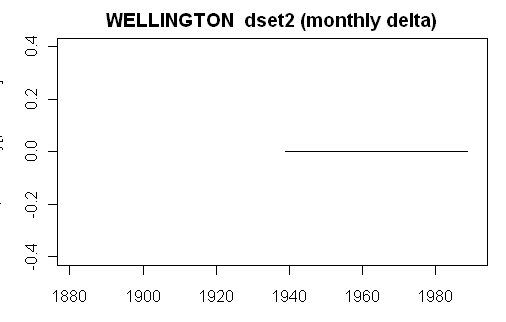
We’ve talked a lot about this station as this has been my template for emulating Step 2. I’m going to show two plots for each station. The first plot shown below is a simple plot showing the difference between the actual Hansen dset 2 adjustment (monthly dset2 minus monthly dset1) and my emulation. Zeros all the way through here. So this one’s been nailed.
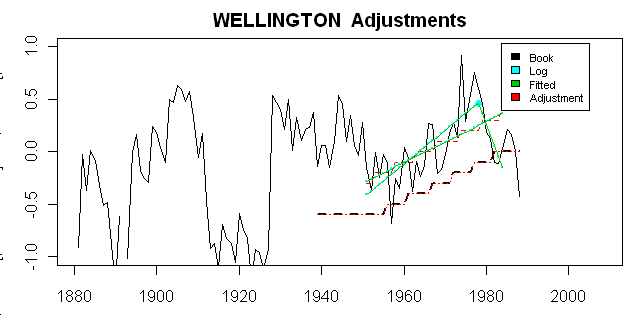
Next, as before, is a more detailed diagnostic plot, showing a variety or relevant adjustment information:
1) the actual rural reference minus the dset1 target (black solid) that gives rise to the observed adjustment (black dashed).
2) in green, the two-legged and one-legged fits over the M0 period (3-stations).
3) cyan – interpreted fit using values extracted from Hansen’s PAPARS.list file. All the values in Hansen’s log were divided by 10 to yield deg C. In this case, Hansen shows two positive slopes, but the results here require that the 2nd slope be negative. There are some remaining puzzles in the PAPARS.list file.
4) red – one of the two fits (two-legged or one-legged) is selected according to an interpretation of Hansen’s flagging method and rounded to 0.1 deg C, yielding steps. The graphic also shows a displacement of the selected fit zeroed to the end of the M0 period, again rounded to 0.1 deg C. This is the series that matches the observed Hansen adjustment in this and other cases.
In this case, Hansen has displaced the two-legged fit (said in the articles to have been used) with a one-legged fit, nowhere mentioned in the original articles.
Stepping back a little from the esotrica of decoding the Hansen codex, one know ponders whether the adjustment makes any sense and here I urge you to look particularly at the extrapolated periods. The adjustment, such as it is, is fitted to the M0 period (3 stations), but is extended by 50% to periods with less than 3 stations. The extrapolated adjustment does not consider the behavior of the reference series/target delta (the underlying black plot), but instead simply projects the closing values at either end of the M0 period. So in this case, there is a two fold whammy. The actual difference declines sharply in the 1980s, but the adjustment remains at high levels. But before 1951, the actual difference increases sharply, but the adjustment remains at low levels. Viewed as a statistical methodology, it’s hard to imagine a stranger procedure. I wonder what Wegman would say.
Batticaloa
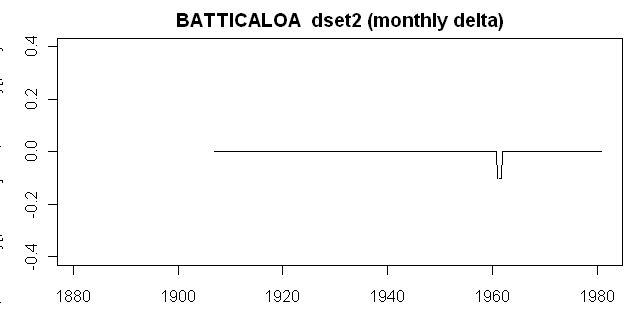
Batticaloa (Sri Lanka) is another station with only a few comparanda (only 3 rural stations). Again, the first graphic demonstrates the emulation of the Hansen adjustment has been successful with only a 0.1 deg C adjustment in one year unresolved.
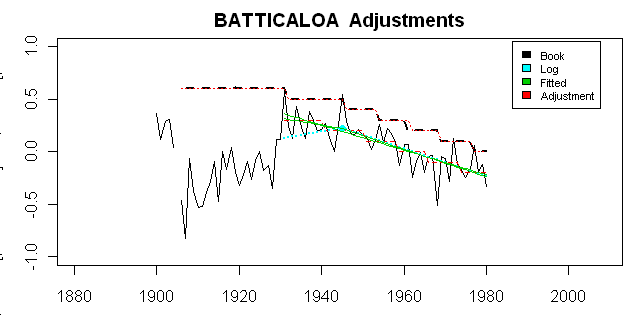
Now here is the more detailed plot of adjustments, corresponding to the Wellington NZ plot. Again, the accuracy of the emulation is evident. Again, I urge you to look at the behavior in the extensions. You have to eyeball the fit a little since Hansen has displaced the fit (and I’ve only shown the extrapolation matching the displaced Hansen version, but the eyeballing is easy.) Once again, the extrapolation in the early portion yields a very poor fit. In this case, the actual delta declines, while the fit is left at high levels. In both cases, the fits don’t make any sense. Perhaps the nonsense cancels out overall, but maybe it doesn’t. But why have this sort of crap in software that supposedly meets NASA standards.
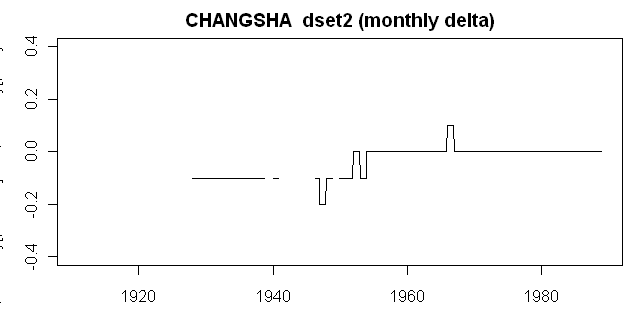
Changsha
Wellington NZ had only 4 comparanda, Battocaloa only 3 comparanda, but Changsha had 20 “rural” comparanda and tests a few more components. Here is the comparison of the emulated and observed adjustments. Right on for recent periods, but 0.1 deg C off in the early portion, for reasons as yet unknown.
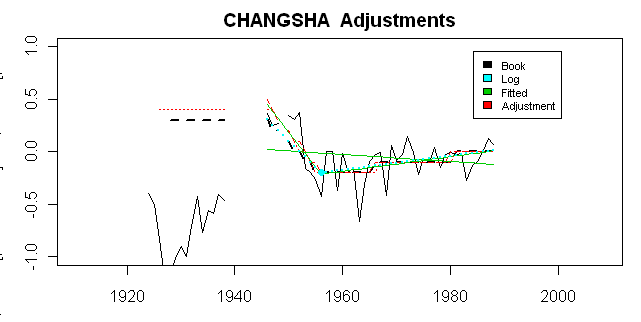
Next, here is the comparison graphic using the same routines as for the above two cases. While the emulated and final adjustments match, the plot from the PAPARS log parameters (cyan) doesn’t match.
This discrepancy can be patched by changing the sign of the slopes preserved in the PAPARS log. Why? Who knows? Another GISTEMP zip, bop and whirr. Aside from this, once again, we have a bewildering extrapolation. In this case, there is a disconnected piece of the Changsha record, which ends in 1938, re-starting only after World War 2. The two pieces of the Changsha record come from one version and therefore Hansen doesn’t bother with quality control details (he requires a 10 year separation and different versions before it catches his attention.) Although the pre-1938 piece seems disconnected, nonetheless Hansen extrapolates the 1946 adjustment for the extension of the record back to 1926.
There’s another interesting feature to this example. We’ve already seen reprehensible handling of Chinese data by Jones et al [1990], an often cited study, where they claimed to have inspected station metadata, but there is convincing evidence that the station metadata did not exist. (Their defence against Doug Keenan’s complaint appears to be that the station metadata, having survived the Japanese invasion, World War 2, the Great Leap Forward, the Cultural Revolution etc, was “lost” by modern climate scientists in the IPCC period.)
Anyway one of Hansen’s “rural” comparanda for Changsha was Yueyang. According to Wikipedia, it has a population of 5.1 million.
Do It Yourself
If you want to inspect Hansen adjustments for a station of your choice, here is a script. Watch out for quotation marks if you paste from WordPress, which screws them up.
First load collated versions of Hansen data, laboriously prepared by yours truly. This gives you giss.dset1, giss.dset2, giss.anom (annual anomaly version), stations (giss information), station_versions ( a separate info file of versions in use) and two PAPARS logs (one has been re-zipped in gz from a Hansen format, both to read easier, and, as it turned out, using about 25% of the space of the Hansen zip) plus a file of functions.
#1. Benchmark Station Data
loc.giss=”http://data.climateaudit.org/data/giss”
download.file( file.path(loc.giss,”giss.dset1.tab”),”temp.dat”,mode=”wb”); load(“temp.dat”)
download.file( file.path(loc.giss,”giss.dset2.tab”),”temp.dat”,mode=”wb”); load(“temp.dat”)
download.file( file.path(loc.giss,”giss.anom.tab”),”temp.dat”,mode=”wb”); load(“temp.dat”)#. Station Infor
loc.giss=”http://data.climateaudit.org/data/giss”
url= file.path(loc.giss,”giss.info.dat”)
stations=read.table(url,sep=”\t”,header=TRUE,fill=TRUE,quote=””)
names(stations)[3]=”name”
download.file( file.path(loc.giss,”station_versions.tab”),”temp.dat”,mode=”wb”); load(“temp.dat”)
pi180=pi/180;R= 6372.795 #earth’s radius in km#3. PAPARS info
download.file(“http://data.climateaudit.org/data/giss/step2/PApars.statn.log.GHCN.CL.1000.gz”, “temp.gz”,mode = “wb”)
handle=gzfile(“temp.gz”)
paparsghcn.log =readLines(handle)
length(paparsghcn.log ) # 197043
close(handle)download.file(“http://data.climateaudit.org/data/giss/step2/PApars.list”, “temp.dat”)
paparslist=readLines(“temp.dat”) #11229K
length(paparslist) #3530####FUNCTIONS
source(“http://data.climateaudit.org/scripts/station/giss/step2.functions.txt”)
The required data can be calculated for a given station by using the id number (look it up in the stations.tab directory) as follows:
id0=”50793436001″
W=emulate_dset2(id0)
log0=extract.log(id0)
That’s all you need to do. Do check the first plot, simply go:
plot1(W)
To do the second plot, go:
plot2(W,log0)
To check out the selections in the rural network, go:
ruralcompare(W,log0)
I might add a little more to this. There’s lots of underlying info in the W object. Get back to me if you run this and come up with anything odd. This is very far from being final or production quality, but at least it’s beginning to clear away the underbrush of the grotesque Hansen code.





71 Comments
This looks like string theory, silly string theory. My hat is off to you for wading through this. I tried last year and gave up because I found the excercise maddening.
Blind automation cannot create truly representative adjustments for each station.
Obviously, in statistical terms, the Hansen methodology seems demented. But whether the demented adjustments “matter” is another question.
Perhaps they all just cancel out and the machine just goes zip, bop and whirr without actually making matters worse than making no “urban adjustments” at all. That’s a topic for another day or another month.
What we are increasingly in a position to say is that its seems very unlikely that the adjustments perform the adjustment for the urban effect that they are said to do. It’s been noted on other occasions that the positive “urban” adjustments are nearly as common as negative adjustments.
In the three cases here, the weakness of the early data in the ROW (the Where’s Waldo problem) emerges once again. Hansen’s methods with weak data seem completely unsatisfactory. In a situation like the continental US, where there is a substantial network of QCed rural data (USHCN), it seems that even Hansen is unable to wreck the data, but in places like China, it looks like a different story entirely.
#1. Anthony, the crying need right now is the establishment of meta data for ROW stations. It would have been nice to have more international response of the surfacestations.org type. Too bad we don’t seem able to inspire people in finite areas like NZ to do their stations. A merre four stations in NZ would go a long way:
station version name long lat alt dist urban lights weights
6299 50793615000 507936150000 HOKITIKA AERO 170.98 -42.72 40 352.9568 R B 0.6470432
6288 50793112000 507931120000 WHENUAPAI 174.63 -36.78 27 502.9568 R C 0.4970432
6287 50793012000 507930120000 KAITAIA 173.27 -35.13 87 699.1342 R A 0.3008658
6307 50793987000 507939870000 CHATHAM ISLAN -176.57 -43.95 49 764.8304 R A 0.2351696
But we need history plus modern.
Steve,
Can the occasional adjustment error be caused by using different rounding methods (round-half-up and round-to-even)?
Steve, congratulations on all your hard work. But I’m confused by the results. Is there a somewhat simplified explanation of what I’m looking at here in the graphs? It looks like the solid black line is raw data. But what are one and two legged fits? By M0 period, I assume you mean the period of temp measurement overlap for the station in question and the nearby stations?
A tip of the hat to Steve for doing the impossible. And no one has even looked at this before CA! I am afraid I must self-snip what I think about these adjustments. It just looks *&^**# and *@@#$#%. Oops, sorry.
I’ve had some offers for an international effort, but managing it all is beyond my current capability.
Here is a station list from UCAR that may be helpful in determinign what type of station it is.
http://www.rap.ucar.edu/weather/surface/stations.txt
Here is what METADATA is available from NCDC MMS and what I’ve been able to derive:
HOKITIKA AERO 93615 is between the airport runway, the city, and the ocean -42.71667 170.98333 apparently an AWS
here is a Google Earth Map link
WHENUAPAI (Air Force Base) 93112 -36.78 174.61667 appears the be at the SW end of the runway. The latitude is coarse, so pinpoiting it exactly is difficult, but it may be the square fenced in area in the center of the screen
Google Earth Map link
Here is more metadata on it from Sinan: http://www.unur.com/climate/ghcn-v2/507/93112.html
(You and I are both referenced at this page: http://www.unur.com/climate/ghcn-v2/ )
Sinan has the metadata on NZ stations here:
http://www.unur.com/climate/ghcn-v2/507/index.html
KAITAIA (airport) 93012 again the latitude is coarse -35.1,173.26667
Google Earth Map link misses the airport, and the photo res is not good enough for me to spot the station
CHATHAM ISLAND 93987 is an automated station on a peninsula into the sea. It appears quite rural, and I think I have locate the station via Google Earth imagery here
see the link
Based on my experience in spotting stations, it looks to be the small fenced in area directly in the center of the screen to the west of the facility with the large satellite dish the latitude/lon is again coarse, -43.95 -176.56667 but not far from what I perceiev the station to be.
Wish I had more.
Anthony, all the GHCN metadata is in my information file giss.info. It’s the same as Sinan’s info.
As you say, Chatham Is;and is rural. The issues here relate to seeming discontinuties in the deeper history and station history info is what’s specifically needed.
It looks like there is a picture of the Hokitika Airport weather station in the background of this picture:
Re Surfacestation.org abroad I had a look at the UK ones – all the ones within driving distance of me are on military airfields, the chances of being able to get on to them, take photos and not be arrested are slim, so sorry I can’t help over here. But I did look at the Rothamstead “problem” which has a huge influence on the Central England Temperature record – link – to which David Parker kindly replied.
Hansen has just posted an article on the Guardians, comment is free, site.
http://www.guardian.co.uk/commentisfree/2008/jun/23/climatechange.carbonemissions1
You might ask him directly what he thinks counts a rural and why the past seems to be getting colder.
#8 Steve
I’ve started trying to do a map of the Australian Climate Reference Station Network (Bureau of Met) to the GISS stations. There are a lot of airports in that network – many are not highly developed.
I can’t access GISS.INFO to cross-check stations from the link above?
re9 tty, good find
Actually this looks more like the machine that goes “ping!”, which sits right next to the most expensive machine…
Sorry off topic but, is not an underground low-loss primary power grid still a bit futuristic? Does Hansen have EE insight I am missing? I am all for improving the grid for wind power etc additions, but buried high voltage lines?
The comments were there when I started reading. Now they are gone! I guess they don’t want any more comments.
Re #3
OK NZ. Let’s see some pictures and info!
Please!
Re: No. 16 – The whole point of the requirement for an “underground low-loss primary power grid” is to triple or quadruple (or more) the cost of the primary grid, making locally generated wind and/or solar power cost-competitive with the (then) hugely more expensive grid power. Then all will be able to pay much higher prices for power, and feel morally superior for doing so. See?
ref 19 Oh now I understand! Silly me and cost conscientious.
For Anthony Watts
Could do Hokitika, NZ for you if you want, and if I can find a digital camera?
Rob R
One last thing before I’m back to lurking, “fetid grubs and maggots” should be changed to fetid maggots. Grubs are a good source of protein and superior to anything Hansen has produced IMHO. Steven is demeaning grubs.
Speaking of grubs and maggots:
http://www.foxnews.com/story/0,2933,370521,00.html
The heads of major fossil-fuel companies who spread disinformation about global warming should be “tried for high crimes against humanity and nature,” according to a leading climate scientist.
Dr. James Hansen, director of the NASA Goddard Institute for Space Studies in New York, sounded the alarm about global warming in testimony before a Senate subcommittee exactly 20 years ago.
He returned to the topic Monday with a speech at the National Press Club in Washington, D.C., given to the Worldwatch Institute.
My reference was to “a leading climate scientist”, not others.
RE20 Rob R. yes please, photos are good but station history is what Steve Mc really needs.
See surfacestations.org for info on how to survey
RE8 Steve Mc I have a line in with the NZ met office with help of my friend Bob Carter. Will advise.
Steve
With respect to the New Zealand sites the closest one to me would be WHENUAPAI. However this is a military airport (at least at the moment – it is scheduled to close as a military base in 2012 and open up to civilian traffic). I very much doubt that I’d be able to get onto the site to take any photos due to its military use.
I’ve been through HOKITIKA once – and it is pretty rural. Couldn’t see all that much though as it is also one of the wettest places in New Zealand. Its climate is about as different to that of Wellington’s as you can get as it is trapped between the foothills of the Southern Alps and the edge of the Tasman Sea. With the prevailing winds coming from the west it has a huge amount of rainfall dumped on it, often in very short periods of time.
CHATHAM ISLAND is at the most southerly point of New Zealand – I haven’t been there and doubt all that many people have – it is very lightly populated and a bit of a joke around the rest of NZ as being at the back end of nowhere in a country that is, itself, the back end of nowhere!
Can’t say much about KAITAIA, I plan on heading up that way over summer (so 6 months time) but not in the near future.
Is there a definitive list of NZ weather stations anywhere? If so then I’ll happily take some snaps of nearby weather stations.
Oops, confused Chatham Island with Stewart Island in my last post (not for the first time either). Stewart Island is at the Southern Tip of NZ; Chatham Island is an island off the East Coast of NZ pretty much on the international date line. The islands are administered by New Zealand but are completely different climatically. Can’t say much about them as never been.
Anthony/Steve:
Is this the sort of metadata you need? For example, on Hokitika: http://cliflo.niwa.co.nz/pls/niwp/wstn.sensor_his?cagent=3909
Thanks to Grants lead, here is the complete list of the 4 stations including details on the old and new stations
HOKITIKA AERO
http://cliflo.niwa.co.nz/pls/niwp/wstn.sensor_his?cagent=3909
http://cliflo.niwa.co.nz/pls/niwp/wstn.sensor_his?cagent=3910
WHENUAPAI
http://cliflo.niwa.co.nz/pls/niwp/wstn.stn_details?cAgent=1410
http://cliflo.niwa.co.nz/pls/niwp/wstn.stn_details?cAgent=23976
Kaitaia Aero
http://cliflo.niwa.co.nz/pls/niwp/wstn.stn_details?cAgent=1024
http://cliflo.niwa.co.nz/pls/niwp/wstn.stn_details?cAgent=18183
Chatham Island
http://cliflo.niwa.co.nz/pls/niwp/wstn.stn_details?cAgent=6191
http://cliflo.niwa.co.nz/pls/niwp/wstn.stn_details?cAgent=17840
snip – try not to be angry
#27, 28. Excellent.
It’s a good thing that the government is muzzling Hansen. Otherwise, who knows what he might say next . . .
Maybe he was just having a “senior moment”
Also with Bob Carter’s help, who has actually been to Chatham Island, I have located the station there. My initial target in earlier comments was wrong.
Here is the location via Google Earth link
It is the fenced in area just to the west of the marker on Google Earth, you can see the screen as a small white dot. The screen is 32 meters from the closest building, making it a CRN class 2 station, which is good.
Bob remarks in email exchanges:
Boy! New Zealand doesn’t mess around! Thank you.
Cool. Glad I could help. Can you guys throw a little summer my way in return? Christchurch was COLD last night.
Hi,
I’m no climate expert, but I’m curious. Being a database administrator, I don’t really feel at ease with statistical utilities. But I work at a telecom and there we use database’s analytical tools to analyze much larger amounts of data than GISS.
Usually I just read the posts and the comments. Nevertheless, I’ve been playing around with GISS data after loading it on an Oracle database, and I’ve made a few discoveries. First, there is a lot of duplicate data on the file v2.inv. Worse, some of the duplicates (by station/year/month) actually have different data. My doubt is how does Hansen removes the duplicates (quite easy when it is a full duplicated record, but somewhat more difficult for duplicate records with different data). What value is used? Average, max or min?
Thank for your attention, and back to lurking. And congratulations on your fine blog.
peterblood #35
Sometimes I think it’s just made up on the fly.
#35, 36. Look at past posts on Hansen Step 1 (check left frame Hansen /GISS category) for discussion of how Hansen treats what we’ve termed here as “scribal” variations. It’s very strange, but amounts to another application of his “bias” calculation also exemplifed in a different contewct in Step 2.
Big picture question: In terms of the whether global warming is real and what causes it, why does your analysis matter? All of the temp datasets show the same upward trend. There are several lines of independent evidence that support AGW.
In addition, to surface temp datasets we see increases in SST over decades and increases in ocean heat content. And as AGW predicts we see a cooling in stratosphere, a greater warming trend near poles than near equator. Finally we see increases in all sorts of proxy temp measures like blooming dates, migration dates, breeding dates, melting glaciers, receding ice caps, etc.
Explain all that away.
We have several lines of independent evidence, and try as you might, you can’t ignore so many lines of evidence, just because your suspicious of Hansen and the GISS dataset. That is unless you want to claim a vast coordinated conspiracy by hundreds of researchers working in dozens of independent labs.
So Steve, regarding big picture, how is your analysis relevant?
Streamtracker: For the Big Picture, read Steve’s Presentation at Ohio State University May 16, 2008.
#38 – Streamtracker,
Big-picture answer: The basic question is “what relative proportions of GW are due to natural causes and human-induced causes?” The claim that CO2 increase is the sole or primary cause needs proof beyond correlation and modeling (both processes can only demonstrate some association, not prove cause and effect). First of all, that has meant scrutiny of the data by independent eyes. When that was undertaken by Steve several things were found: 1) sloppy science, 2) invalid statistical analysis, 3) failure to make supplemental information public, 4) funny-business with peer-review, 5) official obfuscation, 6) bad assumptions when analyzing data, 7) extrapolation beyond the data. These all suggest to an auditor that the claims being made are unsupportable (at least for now) and perhaps driven by ideology, personal ambition, or some motive other than trying to understand the climate system so that reasonable action can be taken (assuming that such actions are even possible). The proposed drastic changes to the world’s economies demand better evidence and honestly-done science or a lot of people will suffer horribly from human-induced policy errors that didn’t have to happen. Unfortunately, the various lines of evidence don’t agree perfectly and leave room for different answers to the basic question posed above. Hence the debate. CA is just trying to make the information better.
This isn’t meant to sound like a rant, just a brief distillation of thousands of posts and comments on this blog over the last three years.
#40 This departs from my position in a number of respects. I have never suggested that policy makers not proceed with decisions that make sense based on the information that they receive from formal institutions. If I were a policy maker in high office, that’s what I would do regardless of my views on individual points. I also do not conclude that, merely because the particular papers that I’ve studied are fundamentally flawed, that the standard conclusions cannot be arrived at by alternative reasoning.
I would like to direct readers to such a reference, but one of the fundamental problems in this field seems to be that climate scientists believe that explaining how you go from doubled CO2 to 2.5-3 deg C is too “routine” (in Phil’s words) to be bothered explaining to the public. I’ve had a longstanding request for a reference that shows this in detail that arises above armwaving and have thus far been unsuccessful. Unlike Gary, I do not conclude that this makes everything unsupportable, only that a clear exposition does not seem to exist. I think that climate scientists might well ponder this before blaming Exxon for the supposed obtuseness of the public.
While I’ve encountered much obfuscation, I think that much of this is attributable to a combination of pompousness and excessive defensiveness on the part of individual scientists and an incomplete understanding that, when major policy decisions are involved, an open kimono policy on data and methods is inevitable. They want to have the privileges of advising on world policy but still reserve the preciousness of seminar room behavior.
Really? Is the globe in 2007 or 2008 warmer or colder than 1921? or 1150? Do we really know the answer to that question? There are very few locations around the globe that had a temperature records taken continuously over the last century, and none that haven’t undergone significant changes in equipment and microenvironment. The data shown in IPCC graphs take a large mixture of mediocre and bad data and try to make adjustments to account for these issues. The point (from my perspective) of this thread is to examine the adjustments in detail to understand them, and later to discuss carefully whether they are justified or done properly. Because the adjustments are often as large as the temperature change in the final graph, this is absolutely essential.
Again, all of these data sets that look at temps over, say a century, are full of missing, bad, and uncomparable data. For the SSTs, there is a big adjustment made s made for the type of measurement. But can you really make a straight line comparison between Japanese bucket measurements in the 1800s with American engine intake measurements in the 1990s? If you want to even try, you have to subject the data to very many adjustments, and again, the rationale and appropriateness of the adjustments needs to be looked at carefully, and not in “data not shown” or in a supplemental file that is either unavailable, or hopelessly convoluted.
I can’t speak for the Steve or the other hard working auditors here, but I would suggest that no one here is trying to “explain away” data. That is NOT the point of science – to only focus on data that matches your model. The ideal is to instead to examine the data objectively, and try to test hypothesis and design further experiments. NOT to call people names, or demand they by put on trial for disagreing with you, and to NEVER say science is settled. In science, the case is never closed.
In 38 steamtracker indicates that a warming globe is an implication of AGW theory. It is also an implication of a theory of a climate undergoing natural variations. So evidence that the globe is warming in the last 30 years does not provide a differential between the two theories. The IPCC indicated as much by reporting that the warming prior to 1950 was the result of natural variation but that the warming since then can be attributed to AGW.
The evidence that steamtracker adduced is not definitive evidence of AGW even in the big picture. Ross McKitrick points out that definitive evidence of AGW would be warming at the tropical tropopause. The data does not indicate a warming there. AGW defenders mount two defenses to this failure of the theory
a) the data is wrong
and
b) some AGW models are compatible with the lack of warming.
In other words the data are wrong and are therefore useless or our models have such wide error bars that they are therefore useless.
So one could well ask of AGW proponents, regarding big picture, how is your analysis relevant?
#37
I’ve read the suggested thread, and it appears to be about post-processed GISS data. I didn’t use the processed data, but the raw data – v2.inv for what I understood is the raw data before processing. Actually I’ve loaded the raw file into a table (same structure: country, station, modifier, year, jan, feb, etc), then normalized it with a procedure so that it become country, station, modifier, year, month, data.
That gives a table with about 6M rows. Of these about 1M is simply duplicated data (that is identical rows). About another 500K are ‘duplicate’ records bearing different data. I don’t have now the actual figures as I’m not using my Linux box (the computer that has the data), but these are reasonable estimates for what I recall.
I was able to create 3 tables without duplicate values: first based on min of duplicates, second on max of duplicates and third on average of duplicates (all plus the non duplicated data). On all 3 I was able to create a primary key on country/station/modifier/year/month to verify the uniqueness.
Using those tables to compute unwheighted yearly averages I’ve found discrepancies in some (mostly recent) years. I may check them out if useful. Those are still greater if the raw data (including all duplicates) is used where some years present differences over 1C.
re 28
For the Chathams stns you need to look at agent 6175 PO radio 1878 to 1958, and also agent 6176 Waitangi 1956 t0 1994
The Chathams is definitely rural with the total population for the island group less than 700.
Whenuapai should be classed as urban because it is an airfield slap in the middle of the Auckland metro area pop at least 1Million
Re peterbloods comments, as far as I can tell v2.inv is the master list of stations, indexed by an 11 digit station ID. The version I have does not contain any duplicates. The actual data used at the start of step 2 is ts.txt. This contains monthly data for a subset of the stations in v2.inv, and uses a 12 digit id. The extra digit appears to be used to distinguish different data series for the same station – it looks as if up to 3 series are allowed for any station in text_to_binary.f, and so far as I’ve got through the code (mid-way through papars.f) it looks as if the series are treated completely independently.
In my copious spare time, I’m trying to duplicate the test results here:
ftp://data.giss.nasa.gov/pub/gistemp/GISS_Obs_analysis/test/STEP2/test1/
It looks as if the analysis in papars.f is done on annual anomaly data, where the annual anomaly is calculated as the mean of up to four seasonal values, each calculated as the mean of up to three monthly values, with a year staring in December. Why the average is not simply done over monthly anomalies is not explained. I’m up to the CMBINE subroutine, in which the rural time series are combined in a curious fashion – rather than just calculating a weighted average, using inverse distance from the rural station as the weight, an extra “bias” factor is added to each new series, apparently to give it the same mean as the average calculated so far. The rationale for this is not explained.
That should read “inverse distance from the urban station as the weight”
Steve,
You’ve done an impressive piece of work decoding the GISS code.
I tried running the R code on a few stations, and it seems the discrepancy in slope for Batticaloa and Changsha can be traced back to the extract.log function. There is a piece of code apparently intended to remove the dashes between the M0 and M1 years. Unfortunately a side effect is the removal of the signs for the miscellaneous slopes as well. One possible fix that for this is highlighted below.
extract.log # removed: test2[2]=gsub(“-“,” “,test2[2])
dashpos = regexpr(“[[:digit:]]{4}-“,test2[2])+4
substring(test2[2], dashpos, dashpos )
writeLines(test2,”temp.dat”)
test2=read.table(“temp.dat”,colClasses=c(“character”,rep(“numeric”,13)),skip=1)
name0=c(scan(“temp.dat”,n=9,what=””),”M0_start”,”M0_end”,”M1_start”,”M1_end”,”flag”)
name0[2:3]=c(“sl1″,”sl2”)
names(test2)=name0
extract.log=list(test1,test2)
extract.log
}
The plot2 function has to be changed accordingly of course (note that both sl1 and sl2 have the same signs here now, and sgn0 may be removed if so desired:
temp=(x =a$knee);sum(temp)
points( x[temp], sgn0*0.1*(a$Yknee + a$sl2*(x[temp]-xmid) ) ,col=5,pch=19,cex=.1)
Steve: Good spotting.
Seems my first post had some HTML problems, so I’m trying again.
Steve,
You’ve done an impressive piece of work decoding the GISS code.
I tried running the R code on a few stations, and it seems the discrepancy in slope for Batticaloa and Changsha can be traced back to the extract.log function. There is a piece of code apparently intended to remove the dashes between the M0 and M1 years. Unfortunately a side effect is the removal of the signs for the miscellaneous slopes as well. One possible fix that for this is highlighted below.
extract.log
# removed: test2[2]=gsub(“-“,” “,test2[2])
dashpos = regexpr(“[[:digit:]]{4}-“,test2[2])+4
substring(test2[2], dashpos, dashpos )
writeLines(test2,”temp.dat”)
test2=read.table(“temp.dat”,colClasses=c(“character”,rep(“numeric”,13)),skip=1)
name0=c(scan(“temp.dat”,n=9,what=””),”M0_start”,”M0_end”,”M1_start”,”M1_end”,”flag”)
name0[2:3]=c(“sl1″,”sl2”)
names(test2)=name0
extract.log=list(test1,test2)
extract.log
}
The plot2 function has to be changed accordingly of course (note that both sl1 and sl2 have the same signs here now, and sgn0 may be removed if so desired:
temp=(x =a$knee);sum(temp)
points( x[temp], sgn0*0.1*(a$Yknee + a$sl2*(x[temp]-xmid) ) ,col=5,pch=19,cex=.1)
Steve, instead of me filling up the blog with similar messages, I hope you can help cleaning up the message and delete any duplicates. I think there is still enough code left to see what I tried to accomplish 🙂
Regards
We have several lines of independent evidence, and try as you might, you can’t ignore so many lines of evidence.
streamtracker, the “evidence” is the problem. To begin with….
#46
Right. v2.inv is the station inventory. I guess that’s where the .inv came from. The temps I’ve loaded were from v2.mean. I’ve turned on the Linux to check that out. Now why would they have duplicate data there is quite stange. As I’m here I can also check for the loaded data: all data tables have columns country_cod, wmo_station, modifier, year, month, data. When loading all the -9999 values were discarded and I ended up with a 6,724,329 rows. My blues started when I tried to create a primary key on the table (that should be country_cod, wmo_station, modifier, year, month) to speed up searching. Oracle refused as there were duplicate keys. So I searched for them. First I’ve created a table with all duplicate values (674,193 rows) and another with non duplicate values (that would be the first one minus the duplicates) but I found out that the duplicate key problem subsided. So it was rows with the same key but different data.
So I created another table that didn’t include duplicates or duplicate keys (3,926,636 rows). That’s just a little over half rows without any problem. With the duplicates and duplicate keys I did build 3 additional tables using minimum, maximum and average of data (grouped by the key) and by that I got rid of duplicate values. Adding the non-duplicate values I’ve obtained 3 tables with 4,985,412 rows each. My doubts: why are there about 1,000,000 dubious values? And how does Hansen algorithm copes with that?
I decoded the v2.inv long ago and have this data in an organized form – look in the CA/data directory.
#53
I’ve loaded v2.inv with this script (for sqlldr):
load data
infile ‘v2.inv’
append
into table stations
(country_cod position(01:03) char,
wmo_station position(04:08) char,
modifier position(09:11) char,
station_name position(13:42) char,
latit position(44:49) decimal external,
longit position(51:57) decimal external,
extra_1 position(59:62) integer external,
extra_2 position(64:67) integer external,
flag_1 position(68:68) char,
extra_3 position(70:73) integer external,
flags position(74:84) char,
environment position(85:89) char,
ambiance position(90:100) char,
type_1 position(101:101) char,
type_2 position(102:102) integer external,
extra_4 position(104:106) integer external)
I wasn’t able to decode the meaning for columns extra_n and flag_n – they’re still loaded anyway.
Hey, folks, NASA are shadowing us. Check out
ftp://data.giss.nasa.gov/pub/gistemp/GISS_Obs_analysis/ARCHIVE/Steve/
which contains some Papars info for Wellington with files dated June 20-21, 2008. I guess they don’t joust with jesters, they just put agents scouting their moves.
Hey, Jim and Reto, don’t be shy. You can say hello.
This would be any warming and not just enhanced GH warming. Ross is wrong on this point.
Have mosher start your car for you. 🙂
I have been playing around a bit, running these scripts on different stations, and there are some interesting things happening. For instance, when trying the urban station 42572231006 (New Orleans audobon), the R scripts find a lot more rural stations than the fortran code does.
It seems this can be traced down to the Papars.f file and how it decides whether a station is urban or rural. This has been discussed on this blog earlier, but it boils down to the following:
IF(NAME(31:32).EQ.’ R’.or.NAME(31:31).EQ.’1′) THEN
rural
ELSE
urban
And, in the input file, a numeric code (1,2,3) for lighting will be placed in NAME(31), and as such will have presedence over the ‘R’ in NAME(32).
For instance, the station with ID 722330020 has NAME(31:36)=”2RB425″. Thus, in spite of the ‘R’, this is considered an urban station because of the ‘2’ which is the brightness index (1=dark and 3=bright). Now, the station_versions.tab file does not seem to contain the numeric brightness index, so thus far I have been unable to have a “correct” set of rural stations, I just get too many. A small adjustment to the ruralstation() function could have corrected this if the brightness index had been there.
Here are the superfluous station IDs for this particular case:
722330020 722330010 722310080 722330040 722310040 722330060 722350020 747550020 747550030 722350050 722340020 722350040 722350030 722350060 747770050 722340030 722340040 722350100 722210000 747530020 722340060 722290010 722350120 747780010 722430050 747690050 747690070 723340020 722200010 722480030
(The ‘2RB425’ code can be found in the file Ts.GHCN.CL.2.txt)
Hmmm, I just discovered the R code to generate the station_versions.tab file (http://data.climateaudit.org/scripts/station/giss/collation.giss.anom.txt), might try to adjust it and be back later….
Thor, this code is set up for the ROW right now. We discussed the USHCN codes a while back and I’m well aware of it, but am trying to focus on the ROW. So don’t worry about the US right now. I know what to do and will do it another day.
Ok, in that case I will play with the rest of the world instead.
BTW, when taking the brightness code into account, the rural station set was equal to the one from papars.f
Steve, when I look at the blip in your Batticaloa adjustment versus the GISS adjustment, I see it falls roughly in the middle of the downward slope and simply reflects you extending the +.3 adjustment by one year versus GISS extending the +.2 adjustment by one year. So could the difference between yours and theirs be nothing more than rounding?
Steve, given what Thor said in #48, do you have new plots for Changsha and Batticaloa?
#55 Steve – I take that as a positive sign. The few email exchanges I have had with them have been responsive and thorough, and I believe they will ultimately allow facts to prevail. That they are taking a look at Wellington means they take the example we’ve highlighted seriously. They know the code, but perhaps have not looked at the influence of individual data points as closely as we have. It would be nice if we were provided with a detailed and accurate algorithm of the adjustment (and other steps).
Call me naive, but have you seen anything like this from Mann?
#61, The plots are OK. I had to patch the slopes to make the graphs work, but the reason for the patch was the read problem. If I went back and fixed that, it would just take a patch out, but wouldn’t change the plots, which, as to this issue, are OK.
#60. I’m ure that it’s rounding arising from rounding occurring at a slightly different step. I’m not going to worry about it right now. I’m trying to decode Step 3.
#62. Well, they have been totally unresponsive to my emails right from the start. I sent them a number of straightforward inquiries last year which were ignored. Some of these folks (e.g. Esper) blacklisted me prior even to the start of Climate Audit, merely for having the temerity to criticize Mann. I was told by television producer that a condition of Hansen’s interview with him was that my name could not be uttered.
Yes, we’ve seen some of Mann’s code, which was produced only at the request of the House Energy and Commerce Committee – and this only after he drew attention to himself by telling the Wall St Journal that he wouldn’t disclose his algorithm. However Mann’s code was incomplete and did not work with any available data sets. It showed however that he calculated the verification r2 statistics, that he later denied ever calculating.
Hansen did not disclose his code willingly either. I asked to see his code in order to analyze questions that led to the Y2K problem – he refused. Even after the Y2K problem was identified, he refused. But that issue got a lot of publicity and this was one issue and one occasion where his bosses were able to tell him to do something and it appears that they made him disclose his code. But it was done very unwillingly.
Hansen’s code disclosure is far more thorough than Mann’s. However, it’s even more opaque than Mann’s which hardly seemed possible ahead of time.
65 (SM) He Who Must Not Be Named. I just love it.
===============================
Re: 62
The only positive thing is that they did not name the folder 666 or Beezelbub.
Jeez # 62
“Beelzebub”? Two interchangeable spellings or two different entities?
I note that Hansen has been claiming to be censored for almost 20 years at least, according to this 1989 NYT article (see):
He’s gotten a lot of press for someone whose views are “suppressed”.
Steamtracker (38),
What Gary (40) said. And let me add this — given the enormous impact that the proposed policy changes will have on the world, especially the poor, there are moral implications involved.
I think the more interesting question you should be asking is why, given the enormous sums being budgeted, the questions being asked here haven’t already been asked by others years ago?
Where is all the vaunted review process we keep hearing about? Mann’s hockey stick was a revolution which completely wiped out everything scientists had known for centuries about the MWP and Little Ice Age. Despite the drastic rewriting of history, it became science gospel less than a year after it came out. And no one checked his data and no one checked his stats. The worst abuse is not the disaster that Mann’s study turned out to be. It is the fact that no one connected to the IPCC bothered to check his work. That alone ought to frighten every person on the planet right down to the toes.
GISS analysis code is being converted into all Python. Hopefully that won’t take too long.
Update page.