-
Tip Jar
-
Pages
-
Categories
-
Articles
-
Blogroll
- Accuweather Blogs
- Andrew Revkin
- Anthony Watts
- Bishop Hill
- Bob Tisdale
- Dan Hughes
- David Stockwell
- Icecap
- Idsos
- James Annan
- Jeff Id
- Josh Halpern
- Judith Curry
- Keith Kloor
- Klimazweibel
- Lubos Motl
- Lucia's Blackboard
- Matt Briggs
- NASA GISS
- Nature Blogs
- RealClimate
- Roger Pielke Jr
- Roger Pielke Sr
- Roman M
- Science of Doom
- Tamino
- Warwick Hughes
- Watts Up With That
- William Connolley
- WordPress.com
- World Climate Report
-
Favorite posts
-
Links
-
Weblogs and resources
-
Archives
Another Try on the Wall
May 11, 2009 – 6:23 AM
CA readers are well aware that Phil Jones of CRU has jealously refused to provide the surface temperature data set used in the prominent HadCRU temperature index, going so far as to repudiate Freedom of Information requests. Efforts to obtain this data have been chronicled here from time to time. As a result of the previous round of FOI inquiries, we managed to get a (mostly) complete list of station names (but not data) – even the names being refused in the first round of polite requests and subsequent FOI inquiries.
There seems to be a gradual movement away from CRU to the Hadley Center in the ongoing management of this data set, with the Hadley Center seemingly having a much more professional approach to data management, recognizing obligations to the public as well as to their pals. I noticed an interesting statement at a Hadley Center readme today
Q. Where can I get the raw observations?
A. The raw sea-surface temperature observations used to create HadSST2 are taken from ICOADS (International Comprehensive Ocean Atmosphere Data Set). These can be found at http://icoads.noaa.gov/. To obtain the archive of raw land surface temperature observations used to create CRUTEM3, you will need to contact Phil Jones at the Climate Research Unit at the University of East Anglia. Recently archived station reports used to update CRUTEM3 and HadCRUT3 are available from the CRUTEM3 data download page.
Given the above statement is meant to indicate that Jones gives the archive to some people, then his refusal to give the archive to others becomes hard to justify even in “community” terms. If Jones has consistently refused to provide the archive to anyone, this seems to be a circular paper chase.
In any event, I wrote to Dr Kennedy, the maintainer of the webpage, referring to this paragraph and asking him for a copy of the archive in the form that the Hadley Center possessed it. I did not cite the Freedom of Information Act, but will initiate a new round of requests if required.
Mannian Collation by Santer
May 9, 2009 – 10:41 AM
I reported a while ago on Santer’s refusal to provide the T2 and T2LT data as collated. Despite Santer’s rude refusal, PCMDI placed the data online anyway, notifying me that this had been their plan along. I reported on this at the time, but so far haven’t reported on the collated data.
The T2 and T2LT data is now located at http://www-pcmdi.llnl.gov/projects/msu in a reasonably accessible format. I collated the T2 and T2LT “TROP” data sets, each into a time series with 49 columns (representing each of the 49 runs) and as a first cut analysis, took an average of the 49 runs and the count of represented runs up to 2000 (when the population decreases sharply, though a few models are archived up to 2050). This yielded the following interesting graphic:

I was intrigued by the sharp decline in the average of the models around 1960. There were no changes in population at the time (as shown by the count information.)
I cross-checked the data in a couple of different ways, one of which was the following barplot of the maximum value for each of the 49 model-run combinations. The 7th model CNRM3.0_run1 had a very anomalous maximum value of over 13 deg C.

Figure 2. Maximum Value for the 49 PCMDI Model-Run Combinations.
I plotted the values for the 7th model-run combination (from CNRM in France), yielding the following interesting graph, showing some sort of goof in the data as archived. I don’t know whether the error rests with Santer’s collation, with the archiving at PCMDI or with the underlying model. The only thing that we know with considerable certainty is that Santer will say that the error doesn’t “matter”.

Figure 3. Santer Collation of CNRM3.0 Tropical Troposphere Data
When he refused to provide data as collated in response to my original request, Santer had emphasized how easy it was to calculate the T2 and T2LT averages from the terabytes of data at PCMDI:
You should have no problem in accessing exactly the same model and observational datasets that we employed. You will need to do a little work in order to calculate synthetic Microwave Sounding Unit (MSU) temperatures from climate model atmospheric temperature information. This should not pose any difficulties for you. Algorithms for calculating synthetic MSU temperatures have been published by ourselves and others in the peer-reviewed literature. You will also need to calculate spatially-averaged temperature changes from the gridded model and observational data. Again, that should not be too taxing.
Perhaps so. But the operation appears to have enough complexity in it to result in a botched version of the CNRM 3.0 run1 in the PCMDI archive for Santer et al 2008.
UPDATE: The impact of one bad series on the 49-series is not negligible as shown below.

UPDATE: Here’s a comparison of averages of GISS AOM (which apparently does not have volcanic forcing) with GISS EH (which does) – both averages of archived T2 tropical troposphere. I must say that I’m a little surprised by the form of the difference between the two – my understanding was that volcanic impacts were held to be fairly transient, whereas there is a notable displacement of GISS EH relative to GISS AOM around 1960. The step takes place at or near the time of the bad CNRM3.0 splice, resulting in a peculiar similarity between the diagram showing GISS EH versus GISS AOM and the the diagram with and without the bad CNRM run.


Figure: vertical red lines are at 1960.0 and 1965.0.
Documentation of models is said to be available at www-pcmdi.llnl.gov/ipcc/model_documentation/ipcc_model_documentation.php .
Trends using Maximum Likelihood
May 6, 2009 – 5:59 PM
For a seemingly simple topic, the calculation of trends and their confidence intervals has provoked a lot of commentary (see any number of threads at Lucia’s). Today, I’m presenting what I think is an interesting approach to the problem using maximum likelihood. In a way, the approach builds on work that I did last year implementing Brown and Sundberg profile likelihood methods for proxy calibration. The techniques are very concise and, once stated, very obvious. It seems unlikely that there’s anything original in the approach, but, despite all the commentary on trends, I haven’t seen anything analyzing trends in quite the way that I’ve done here (but I’m probably re-tracing steps done elsewhere).
The following figure is one that I’ve used for looking at various time series, shown here for the UAH tropical T2LT series.
There’s quite a bit of information in this graphic. Four different autocorrelation structures are shown here: none (OLS), AR1, ARMA(1,1) and fracdiff. For each autocorrelation structure, the log likelihood is shown for a profile of different slopes.
The maximum likelihood (minimum log likelihood) is similar for each of the 4 autocorrelation models (though OLS is slightly higher than the others), but the confidence intervals are much wider for AR1 and other schemes. In this example, there isn’t much difference between AR1 and more complicated autocorrelation structures (but there are other cases in which the differences are very noticeable.) I’ve also plotted the Santer T2LT ensemble mean trend, which is well outside the 95% confidence interval (using maximum likelihood) – something that we had previously reported applying the (1-r)/(1+r) degrees of freedom adjustment used in Santer et al. (but they only reported results for obsolete data ending in 1999).

Figure 1. Log likelihood for MSU Tropical T2LT, with various autocorrelation models. Note: y-axis should be labelled as |z|.
Here is a corresponding plot for the RSS T2 data. In this case, observations are about halfway between zero and the ensemble mean trend. If someone wishes to argue (a la Santer, Schmidt) that there is no statistically significant difference between observations and the ensemble mean, then they are also obliged to concede that there is no statistically significant difference between observations and zero trend even for RSS TMT.

Note: y-axis should be labelled as |z|.
[Added May 7] Here’s a similar plot for annual CRU NH 1850-2008, showing more texture in the differences between the various autocorrelation models. Zero trend (under fracdiff autocorrelation) is not precluded at a 95% level. However, these graphs show more clearly than the bare statistic that this is a two-edged sword: double the observed trend is likewise not precluded at a 85% level.
 Note: y-axis should be labelled as |z|.
Note: y-axis should be labelled as |z|.
[end update]
Here’s how these plots are done (I’ve placed the method below in a wrapper function). The mle2 function used here is from Ben Bolker’s bbmle package (I suspect that the method could be modified to use the more common mle function).
First, get the MSU tropical T2LT series and then for convenience, center the data and the time series (dividing by 10 to yield changes per decade):
source(“http://data.climateaudit.org/scripts/spaghetti/msu.glb.txt”)) #returns msu.glb
x=msu[,”Trpcs”]
x=x-mean(x);year=c(time(x))/10;Year=year-mean(year)
The mle2 function works by calculating profile likelihoods; to calculate the log-likelihood of a slope, it requires a function yielding the log-likelihood of the slope given the time series. Here I applied a useful attribute of the arima function in R – that the log-likelihood is one of its attributes. I defined a function ar1.lik as follows (note the minus sign):
ar1.lik< -function(b,y=x,t=Year) -arima(y-b*t, order=c(1,0,0),method="ML")$loglik
To facilitate comparison with OLS methods, I also used the arima function with order (0,0,0) to reproduce OLS results (double-checking that this surmise was correct). The following calculates the maximum likelihood slope:
Model.ols = mle2(ols.lik, start = list(b=.01),data=list(y=x,t=Year) );
coef(Model.ols)
# 0.05363612
This is precisely the same as OLS results:
lm( x~Year)$coef[2]
#0.05363613
The bbmle package has a profile function that applies to mle2 output, which has a special-purpose plot attached to it (the style of which I applied in the above graph).
Model.ar1 = mle2(ar1.lik, start = list(b=.01),data=list(y=x,t=Year) );
Profile.ar1=profile(Model.ar1)
plot(Profile.ar1)
In the above graphic combining 4 autocorrelation schemes, I used 4 different likelihood schemes as follows (fracdiff requiring the fracdiff package):
ols.lik< -function(b,y=x,t=Year ) -arima(y-b*t, order=c(0,0,0),method="ML")$loglik
ar1.lik<-function(b,y=x,t=Year) -arima(y-b*t, order=c(1,0,0),method="ML")$loglik
arma1_1.lik<-function(b,y=x,t=Year) – arima(y-b*t, order=c(1,0,1),method="ML")$loglik
fracdiff.lik<-function(b,y=x,t=Year) -fracdiff(y-b*t, nar=1,nma=0)$log.likelihood
For convenience in making the above graphics, I collected the relevant outputs from the mle2 stages as follows:
profile.lik=function(x,method.lik=ar1.lik) { #x is a time series
x=x-mean(x);year=c(time(x))/10;Year=year-mean(year)
fm=lm(x~Year);
Model = mle2(method.lik, start = list(b= fm$coef[2]),data=list(y=x,t=Year));
Profile=profile(Model);
profile.lik=list(model=Model,profile=Profile)
profile.lik
}
The models and profiles for the 4 different autocorrelation structures were then collated into one list as follows:
x=msu[,”Trpcs”]
Model=list()
Model$ols=profile.lik(x,method.lik=ols.lik)
Model$ar1=profile.lik(x,method.lik=ar1.lik)
Model$arm11_1=profile.lik(x,method.lik=arma1_1.lik)
Model$fracdiff=profile.lik(x,method.lik=fracdiff.lik)
I then collected relevant information about the various models into an Info table (which is applied in the plot):
Info=data.frame( sapply (Model,function(A) coef(A$model) ) );names(Info)=”coef”
row.names(Info)=names(Model)
Info$logLik= sapply(Model,function(A) logLik(A$model) )
Info$AIC= sapply(Model,function(A) AIC(A$model) )
Info$BIC= sapply(Model,function(A) BIC(A$model) )
Info$cil95=NA;info$ciu95=NA;
Info[,c(“cil95″,”ciu95”)]= t( sapply(Model, function(A) confint(A$profile) ) )
Info$cil90=NA;info$ciu90=NA;
Info[,c(“cil90″,”ciu90”)]= t( sapply(Model, function(A) confint(A$profile,level=.9) ) )
Info$ci95= (Info$ciu95-Info$cil95)/2
round(Info,4)
# coef logLik cil95 ciu95 cil90 ciu90 ci95
#ols 0.0531 -54.1221 0.0200 0.0863 0.0253 0.0810 0.0332
#ar1 0.0459 198.5281 -0.0804 0.1698 -0.0577 0.1478 0.1251
#arm11_1 0.0453 198.8339 -0.0867 0.1743 -0.0626 0.1512 0.1305
#fracdiff 0.0430 198.2359 -0.0956 0.1773 -0.0700 0.1531 0.1364
I needed a little information Santer trends (already collated):
santer=read.table(“http://data.climateaudit.org/data/models/santer_2008_table1.dat”,skip=1)
names(santer)=c(“item”,”layer”,”trend”,”se”,”sd”,”r1″,”neff”)
row.names(santer)=paste(santer[,1],santer[,2],sep=”_”)
santer=santer[,3:ncol(santer)]
The plot was done easily given the above information. I made a short plot function to simplify repetition with other series:
plotf1=function(Working,info=Info,v0=NA) {
layout(1);par(mar=c(3,4,2,1))
Data=list()
for(i in 1:4) Data[[i]]=as.data.frame(Model[[i]]$profile) #profile.tmt$mle.profile[[i]])
xlim0=1.1*range(Data[[3]]$b)
plot(abs(z)~b,data=Data[[3]],type=”n”,col=4,xlab=””,ylab=””,xlim=xlim0,ylim=c(0,3.5),yaxs=”i”)
col0=c(1,3,5,4)
for (i in 4:1) {
lines(Data[[i]]$b,abs(Data[[i]]$z),col=col0[i]);
points(Data[[i]]$b,abs(Data[[i]]$z),col=col0[i],pch=19,cex=.7);
f1=approxfun(Data[[i]]$b,abs(Data[[i]]$z))
x0= info[i,c(“cil95″,”ciu95″)]; y0=f1(x0)
if(i==2) lines(xy.coords(x0,y0),lty=3,col=”magenta”,lwd=1)
if(i==1) lines(xy.coords(x0,y0),lty=1,col=”magenta”,lwd=2)
x0= info[i,c(“cil90″,”ciu90”)]; y0=f1(x0)
if(i==2) lines(xy.coords(x0,y0),lty=3,col=2,lwd=1)}
if(i==1) lines(xy.coords(x0,y0),lty=1,col=2,lwd=2)
legend(“bottomleft”,fill=c(1,3,5,4,2,”magenta”),legend=c(names(Working),”90% CI”,”95% CI”),cex=.8)
mtext(side=1,line=2,font=2,”Slope (deg C/decade)”)
mtext(side=2,line=2,font=2,”Log Likelihood”)
abline(v=0,lty=2)
abline(v=v0,lty=3,col=2) #Santer
}
The first graphic was rendered by the following command:
plotf1(Working=Model,info=Info,v0=santer$trend[11])
title(“MSU T2LT 1979-2009″)
text(santer$trend[11],.3,pos=1,font=2,”Model Mean Trend”,col=2,cex=0.8)
points( santer$trend[11],0,pch=17,cex=1.6,col=2 )
I think that this is a useful way of looking at information on trends. (I doubt that 30 years is a relevant period to test for long-term persistence under fracdiff – for example, there’s been pretty much one PDO for the entire period, but have rendered it here as well for comparison.)
As noted above, the application of likelihood methods to assess trend confidence intervals under different autocorrelation structures seems so obvious and is so easy to implement that one would expect it to be almost routine. And perhaps it is in some circles, but, if it is, it hasn’t been mentioned in any of the recent climate debate on trends.
Antarctic Sea Ice Re-visited
May 6, 2009 – 9:43 AM
Jeff Id did an interesting post a few days ago on Antarctic sea ice in which he provided the following interesting graphic of Antarctic seaice area anomalies, which, from the texture, is daily, rather than monthly:

Figure 1. Antarctic seaice area anomaly (Jeff Id version)
Jeff’s data reference was to the following webpage at NSIDC, but, to my knowledge, this only provides gridded data in binary form and does not provide information on a daily basis. Last year, I scraped binary gridded data for the Arctic and it’s not a small job. The data has to be scraped on a day by day basis and it took me about half a day on high-speed cable. The scraping program requires a little ingenuity. Then the form of the binary data has to be figured out – which “endian” is it, the location and area of the cells has to be obtained (online in an information area), then the definitions of “area” and “extent” have to be applied. Unless Jeff found some daily data that I couldn’t find, there’s more work in this graphic than most readers realize.
Last year, I’d done this for the Arctic and felt a little out-flanked 🙂 by another blogger managing to scrape data that I hadn’t. So I modified by scraping script, downloaded and organized the Antarctic data and produced my own version of Jeff’s graphic, which is substantially the same, but with a few interesting differences.
In producing one of these graphics, there are 5 satellites, with very short overlaps between the early satellites but a longer overlap between the two most recent – f13 and f15. I checked the overlaps for each pairing – there were noticeable differences, but in the tens of thousands of sq km, not hundreds of thousands of sq km. So I used the data as archived without attempting to make intersatellite adjustments (though that would be desirable in a lengthier exposition) and averaged the two satellites where there was an overlap.
Here’s my version of Jeff’s graphic:

Figure 2. Antarctic seaice area anomaly (Steve Mc version)
While the two graphics are reassuringly similar, as noted above, there are interesting differences. In my version, there’s a remarkable downspike in the latter part of 2008. Re-examining the underlying data, this seems to result from an error in satellite f15 in October 2008 – on October 18, 2008, f15 (improbably) showed Antarctic seaice area of over 4 million sq km less than f13. There were only a few days of huge discrepancies, but they don’t seem to have picked up this error yet. f15 was the same satellite that had problems in the Arctic in February 2009 (discussed at Watt’s Up) and results from this satellite are no longer reported.
I’ll post my scraping scripts up as CA/scripts/seaice/collation.antarctica.txt, but warn that I’ve not tried to make them fully turnkey. I’ve posted daily area and extent in tab-separated ASCII form up to May 3, 2009 at CA/data/seaice/antarctica.csv .
Update: Here is my version of the above graphic without the problematic f15 satellite. A little different than Jeff Id’s, but not enough to worry about for now.

Undergraduate Geologists and Secretary Chu
May 4, 2009 – 6:47 PM
A few years ago, I noticed some interesting presentations by geology undergraduates at the Keck Symposium – see 4 papers online here – describing fossils from the Miocene and Pliocene (both well after the Cretaceous) in the Arctic. Here’s a tree from the Pliocene – which is not “hundreds of millions” of years ago, but the period immediately preceding the very cold Pleistocene.

One of the paper specifically reports on Alaska temperature over the Tertiary (post-dinosaurs: the last 50 million years or so)
In Alaska (paleolatitude of 60°N) the MAT dropped from ca. 11° to 4° C between 12 and 13 Ma with concomitant changes in the vegetation (Wolfe 1997).
This is illustrated with the following graphic:

I’m sure that any geology undergrad could make an excellent reading list for an inquisitive Secretary.
Will Andy Revkin Tee Off on Chu?
May 3, 2009 – 7:34 PM
I don’t like talking about political appointees, but Chu is supposed to be a “scientist”.
If you don’t know the answer to something, it’s a good idea not to pretend that you do. Take a look at Chu’s appearance before the House Energy and Commerce Committee url (h/t reader Gene)
[self-snip]
Chu was there as a scientist. Barton asked Chu how the oil and gas got to the Alaska North- wasn’t it warmer when the organics were laid down?
Chu rose to the bait, in effect foolishly denying that it was warmer up north in the Cretaceous, the date of key Alaska source rocks, attributing the presence of oil and gas in Alaska to continental drift. It “drifted up there”.
Nope.
The most recent source rocks in Alaska were laid down in the Cretaceous – see here.
Four key marine petroleum source rock units were identified, characterized, and mapped in the subsurface to better understand the origin and distribution of petroleum on the North Slope of Alaska. These marine source rocks, from oldest to youngest, include four intervals: (1) Middle–Upper Triassic Shublik Formation, (2) basal condensed section in the Jurassic–Lower Cretaceous Kingak Shale, (3) Cretaceous pebble shale unit, and (4) Cretaceous Hue Shale.
By the Cretaceous, Alaska was more or less in its present position. Here is the relevant map from http://www.scotese.com:

It was still much warmer than the present up in the Arctic in the much more Pliocene (the period before the Pleistocene) only 2 million or so years ago. I did a post a couple of years ago showing some interesting Pliocene tree trunks recovered in situ from Canadian Arctic islands.
This is as bad or worse than some of the Bush malapropisms. Chu’s supposed to be a professional scientist. Chu had better raise his game if he wants to stick in the big leagues. Chu
Here’s an interesting test for Andy Revkin and other science writers. They aren’t shy about teeing off on George Will, who isn’t even a scientist, but will Andy (who’s an excellent reporter in my opinion) pile onto Chu or just give him a pass? Everyone knows the answer.
[self-snip]
Here’s the exchange:
Barton: How did all the oil and gas.get to Alaska and under the Arctic Ocean?
Chu: [Laughs.] This is a complicated story. Oil and gas is the result of hundreds of millions of years of geology and in that time also the plates have moved around and so it’s a combination of where the sources of the ol and gas…
Barton: Isn’t it obvious that it was a lot warmer in Alaska and the North Pole? It wasn’t a big pipeline that we created in Texas …
Chu: There’s continental plates that have been drifting around through the geological ages…
Barton: So It just drifted up there?
Chu: That’s certainly what happened. uh, and it’s a result of things like that.
Chairman: Time has expired.
Spot the Hockey Stick #n
May 3, 2009 – 1:06 PM
In a presentation on April 7, 2009, Steven Chu uses the Graybill strip-bark bristlecone chronology (aka the Mann hockey stick) in a presentation. See page 7 here. (h/t to reader Gene).
The Chu graphic even uses Mann’s overlay of temperatures, opportunistically ending at the high point of 1998.
I wonder how Chu does at identifying the purpose of aluminum tubes.
Truncated SVD and Borehole Reconstructions
May 3, 2009 – 12:57 PM
In recent discussions of Steig’s Antarctic reconstruction, one of the interesting statistical issues is how many principal components to retain. As so often with Team studies, Steig provided no principled reasoning for his selection of 3 PCs, statements about their supposed physical interpretation were untrue and, from some perspectives, the choice of 3 seems opportunistic.
As we’ve discussed previously, the issue of PC retention was a battleground MBH issue and was never resolved in a principled way. After the fact, Mann adduced a retention strategy that was not described in the text and could not be evidenced in other networks. Wahl and Ammann invented an ad hoc argument that the MBH result “converged” (as long as the bristlecones were in); this “convergence” argument is not one that appears in any literature by known statisticians. Although Wegman described this method as having “no statistical integrity”, that did not prevent its sanctification by IPCC AR4 through their benediction of Wahl and Ammann 2007. I won’t review this long and sordid history as we’ve discussed it on many occasions in the past.
Reading some of the interesting posts by the two Jeffs and Ryan O at Jeff Id’s blog on truncated total least squares, I recalled that borehole inversion used truncated SVD. PhilB had done some work on emulating borehole inversion calculations a couple of years ago. I corresponded with him about this, but hadn’t figured out how the calculations actually worked, but recalled that results were very sensitive to retained PCs.
I thought that it would be interesting to re-visit this topic, in part to get another perspective on retention issues in a completely different context and in part to try to get a better handle on borehole reconstructions which we’ve barely touched on over the past few years.
Unfortunately it took me a while to figure out how these calculations. While I think that I can replicate some examples, I’m not 100% sure that I’ve got it right. As usual, I’ve placed materials online, in case readers can improve on what I’ve set out here.
There is an excellent data set of borehole readings at WDCP-Paleo indexed here. Data listings can be accessed from links at the bottom of the page, which in turn links to the data provided in a somewhat annoying html format, though the data can be scraped from the html pages. I’ve placed online a read-function keyed by borehole id, which will be illustrated below. This is set up for North American listings, but can be easily modified for other locations (for other locations, you’ll need to check that calls are lowercase).
Many of the borehole locations are “holes of opportunity” from hard rock mineral exploration in mining camps in northern Ontario and Quebec; many sites are familiar names to me. I might even have visited some of the sites at some point in my life.
Tamino, who stoutly defended NASA’s inability to locate post-1991 data from stations in Peru and Bolivia, had a post on boreholes a while ago, in which his type example was borehole CA-001-0 in Ottawa. This proved an odd choice as a type case as boreholes theoretically are supposed to be away from cities. For the benefit of Tamino and readers unfamiliar with Canadian geography, Ottawa is the capital of Canada. Being from Toronto, I concede urban status to Ottawa somewhat reluctantly, but must do so. Like other urban centers in North America, it’s not an obvious location for mineral exploration and Tamino surprised me a little here. However, Tamino’s readers need not fear that the Canadian federal government is going to be displaced by a mine, as I presume that either this borehole was put down for some purpose other than mineral exploration, unless the location in the database is wrong.
Borehole inversion methods have a long history. The researcher hopes to reconstruct the surface temperature history from a set of depth-temperature measurements using the heat equation. The problem turns out to be very “ill-conditioned” (the literature derives from numerical analysis, rather than statistics though the issues are similar). Therefore, various regularization methods have been adopted over the years, of which the most common appears to be truncated SVD.
Hugo Beltami’s website has many papers on the topic, most of which seem to describe the same methodology in more or less similar terms. Beltrami provides equations and examples, but it still took a while to replicate his methodology and I’m not 100% sure that I’ve got it right, though I’ve got much of it. As a benchmark case, I eventually settled on borehole ca-8813 at Belleterre, Quebec illustrated in Figure 6 of Beltrami et al 1992
The idea behind borehole inversion (expressed here in matrix terms rather than the continuous expressions of the papers):
where
is the downhole temperature,
E is a matrix derived from the heat equation (see Beltrami’s articles for the assertion) and
is the temperature history, expressed typically as a vector (step function).
Where erfc is the standard function,
is heat diffusivity here converted to years,
t is a sequence of time intervals.
The idea is to estimate the history from
by matrix inversions, the mechanics of which are perhaps best seen in the script below.
First download information from the WDCO site for ca-8813 using online tools.
source(“http://www.climateaudit.info/scripts/borehole/functions.borehole.txt”)
belle=read_borehole(id=”ca-8813″)
Data=belle$bore
z=Data$z ;range(z) # 25.98 389.17
Q=T_z=Data$T_z
In this paper, Beltrami used 20-year steps and the period 1000-2000. There has been discussion in the literature over resolution and, in later papers, Beltrami typically uses only 100-years and a 500 year interval. However, for today’s purposes, which are about truncation principles as much as anything, the denser net is advantageous. Thus:
delta=20
t=seq(0,1000,delta);K=length(t); #51 #time per page 175 Beltrami
Next we make the matrix from the heat conduction equation. This could be done in one line using the outer function, but I’ve sacrificed a little elegance for transparency:
M=length(z);K=length(t)
E=array(1,dim=c(M,K-1) )
for( k in 1:(K-1)){
for(j in 1:M) {
E[j,k]= erfc(z[j]/(2*sqrt(Kdiff*t[k]))) – erfc(z[j]/(2*sqrt(Kdiff*t[k+1])))
}}
dim(E) #[1] 44 51
dimnames(E)[[2]]=t[2:K]-delta/2;dimnames(E)[[1]]=z
E[1:3,1:5]
# 10 30 50 70 90
#25.98 -0.4646354 -0.1404778 -0.06778118 -0.04175596 -0.02900359
#34.64 -0.3295700 -0.1609920 -0.08293746 -0.05241155 -0.03690798
#43.3 -0.2229484 -0.1658662 -0.09284768 -0.06062173 -0.04344844
The second term in Beltrami’s equation includes a term for surface heat flow density. I was unable to locate any information on what value was used and the value appears to get washed out in the coefficient. However, I located an interesting map of surface heat flow density http://www.heatflow.und.edu/agus05.ppt and used a value of
wm-2 from the map coloring as an approximation.
q_0=0.04 #deem inspection of map of surface heat flow density
R=q_0*z/Kcond
I did a couple of quick experiments with regression and ridge regression, both of which yielded warnings due to singularity:
A=data.frame(Q,R,E); dim(A) #[1] 44 52
fm=lm(Q~.,data=A);summary(fm) # #OLS fails
# prediction from a rank-deficient fit may be misleading
library(MASS)
fm.ridge=lm.ridge(Q~.,data=A);summary(fm)
#prediction from a rank-deficient fit may be misleading
The regression fails because of problems in inverting the matrix. Beltrami regularizes this by retaining only a few PCs; he reported the retention of all PCs with eigenvalues above 0.025 (page 173), which, for this example, proves to be, 6
MinEigen=.025 #page 173 right column
one=rep(1,M)
A=cbind(one,R,E) #this is matrix desribed on page 173 left column
svd.bore=svd(A)
U=svd.bore$u;d=svd.bore$d;V=svd.bore$v
round(d,5)
#[1] 30.18039 3.04874 0.54588 0.21885 0.07824 0.02507 0.00692
r0=sum(d>MinEigen);r0 #6
According to my original objective, I did some experiments with different numbers of retained PCs.
beta=list();Qhat=list()
for(r in 1:8) {
if(r==1) Sr=as.matrix(1/d[1:r]) else Sr=diag(1/d[1:r])
beta[[r]]=as.matrix(V[,1:r])%*%Sr %*%t(U[,1:r]) %*% Q;
Qhat[[r]]=c(A%*%beta[[r]]); # 5.779109 5.665154 5.569599 5.492003 5.429110
}
Here is the target reconstruction excerpted form Beltrami et al 1992 Figure 6.

Here is my emulation of Beltrami’s methodology On the left, I’ve plotted the original data (black points) with the fits from the first few recons; they all fit more or less perfectly with relatively few PCs. On the right, I’ve plotted the various reconstructions. The recon with 6 PCs looks pretty close to the Beltrami example, but I don’t guarantee it.
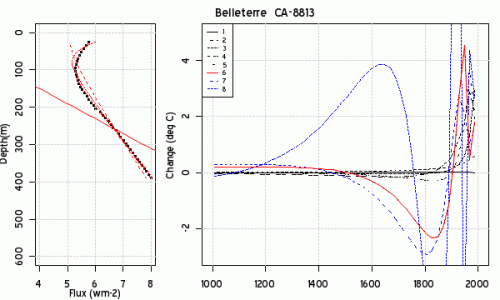
A few comments. As more PCs are added, the results start diverging wildly. I’ve shown up to 8 here, but they get more and more extreme.
Keep in mind that the underlying temperature measurements are smooth. It appears to me that the notches on the right hand side of the reconstruction are artifacts of a 1-dimensional Chladni-type situation, sort of like what we saw in a totally different context with Stahle SWM tree ring network eigenvectors. There’s a reason for this: the coefficients are obtained from the eigenvectors.
Keep in mind here the important and interesting sign change property of eigenvectors in spatially autocorrelated regions that we’ve discussed in the past. The first eigenvector has no sign change; the 2nd has one sign change and so on. I can’t see any reason for using 6 eigenvectors in this case.
At this time, I draw no morale on what any of this means. I simply was interested in seeing how the borehole recons worked and in seeing what principles, if any, were used in SVD truncation. It’s a fairly large topic, but not unconnected with issues that we’ve discussing and may perhaps give an alternative perspective on some issues.
I’m very far from a clear understanding of how much weight can be placed on these borehole reconstructions, but we’re in a much better position to experiment with these matters. If nothing else, the tools may prove helpful to some readers.
References:
Beltrami, H., A. M. Jessop, and J. C. Mareschal. 1992. Ground temperature histories in eastern and central Canada from geothermal measurements: Evidence of climate change. Global Planet. Change 98, no. 2-4: 167–184.
Click to access Beltrami_et_al_1992_GPC.pdf
Beltrami website: http://esrc.stfx.ca/pdf/
Irreproducible Results in PNAS
Apr 24, 2009 – 11:10 AM
In Al Gore’s movie and book An Inconvenient Truth, he presents a graph which he identifies [in the book] as “Dr. Thompson’s Thermometer.” Gore attributes this graph to the ice core research of Lonnie Thompson, and says [in the book] that it provides independent evidence for the validity of the “Hockey Stick” temperature reconstruction of Michael Mann and coauthors.
As it happens, the image Gore presented actually was Mann’s Hockey Stock, spliced together with the post-1850 instrumental record as if they were a single series, and not Thompson’s ice core data at all. See Al Gore and “Dr. Thompson’s Thermometer”.
In fact, Thompson and co-authors really had published an admittedly similar-looking series in Climate Change in 2003, that was supposed to have been the source of the Gore image. (See Gore Science “Advisor” Says That He Has No “Responsibility” for AIT Errors.) But despite Gore’s claim that it measured temperature, Thompson had made no attempt to calibrate it to temperature. Instead, it was an uncalibrated composite Z-score series based on oxygen isotope ratios for 6 ice cores, going back to 1000 AD.
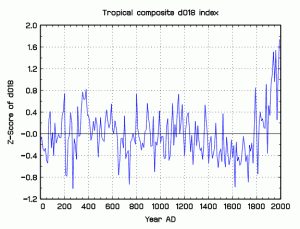
In 2006, Thompson and co-authors published what should have been an even better series, based an additional seventh series and going back 2000 years, in the prestigious Proceedings of the National Academy of Sciences. This “Tropical Composite” Z-score series (TCZ) is shown below. Although again it is not actually calibrated to temperature, it does have the distinctive “Hockey Stick” shape, with only a faint Little Ice Age, and only a trace of a Medieval Warm Period. (Click on images for larger view.)
In a paper that has just been published in Energy and Environment (2009, no. 3), I find that TCZ bears no replicable linear relationship to the 7 ice core isotope ratio series on which it is claimed to be based. The manuscript version with full text and supporting data is online here.