March 2106

Jul 4, 2009 – 9:53 PM

According to KNMI’s version of UKMO CM3, in March 2106, the tropics (20S-20N) will temporarily have an inhospitable temperature of 0.1E21.

In a statement, the Hadley Center said that these results showed that the situation was “worse than we thought”. In an interview, Stefan Rahmstorf said that not only was it worse than we thought, it was happening faster than we thought. Using the most recent and most sophisticated parallel-universe embedded canonical manifold multismoothing of Simpson et al, (H. Simpson et al, Springfield Gazette, June 11, 2009), Rahmstorf said that we could expect a temperature of 0.1E19 by 2020. [For realclimate readers, I’m just joking – they didn’t really say that.]

If any life survives, it will fortunately revert to more hospitable temperatures in April 2106. Below is a screenshot of my download.

By Stephen McIntyre | Posted in Modeling | Comments (124)

The Secret of the Rahmstorf "Non-Linear Trend Line"

Jul 3, 2009 – 9:35 AM

Since the publication of Rahmstorf et al 2007, a highly influential comparison of models to observations, David Stockwell has made a concerted effort to figure out how Rahmstorf smoothing worked. I now have a copy of the program and have worked through the linear algebra. It turns out that Rahmstorf has pulled an elaborate practical joke on the Community, as I’ll show below. It must have taken all of Rahmstorf’s will-power to have kept the joke to himself for so long and the punch-line (see below) is worth savoring.

Rahmstorf et al oracularly described Rahm-smoothing using big words like “embedding period” and the interesting concept of a “nonlinear…line”:

All trends are nonlinear trend lines and are computed with an embedding period of 11 years and a minimum roughness criterion at the end (6 – Moore et al EOS 2005) …

David’s efforts to obtain further particulars were stonewalled by Rahmstorf in a manner not unreminiscent of fellow realclimatescientists Steig and Mann. I won’t recap the stonewalling history on this occasion – it’s worth doing on another occasion but I want to focus on Rahmstorf’s practical joke today.

In April 2008, a year after publication, Rahmstorf stated at landshape.org and RC that:

The smoothing algorithm we used is the SSA algorithm \copyright by Aslak Grinsted (2004), distributed in the matlab file ssatrend.m.

Unfortunaely Matlab did not actually “distribute” the file ssatrend.m, nor were David Stockwell and his commenters able to obtain the file at the time. When asked by UC (a highly competent academic statistician) where the file could be located, Rahmstorf, following GARP procedures, broke off communications.

A year later, I’m pleased to report that ssatrend.m and companion files ( \copyright Aslak Grinsted) may be downloaded from CA here – see the zip file. I’ve placed the supporting article Moore et al (EOS 2005) online here .

I transliterated ssatrend.m and its various functions into an R script here – see the function ssatrend.

Underneath the high-falutin’ language of “embedding dimension” and so on is some very elementary linear algebra. It’s hard to contemplate a linear algebra joke but this is one.

First of all, they calculate the “unbiased” autocovariances up to the “embedding dimension” – the “embedding dimension” proves to be nothing more than a big boy word for the number of lags (M) that are retained. This is turned into a MxM symmetric (“toeplitz”) matrix and the SVD is calculated, yielding M eigenvectors.

Another way of looking at this calculation step is to construct M copies of the time series of interest, with each column lagged one time step relative to the prior column, and then do a SVD of the rectangular matrix. (Some microscopic differences arise, but they are not material to the answer.) In this sort of situation, the first eigenvector assigns approximately equal weights to all M (say 11) copies. So the first eigenvector is very closely approximated by

1/\sqrt{11}, \ldots , 1/\sqrt{11}

They ultimately retain only one eigenvector (E in the ssatrend code), so the properties of lower order eigenvectors are immaterial. Following through the active parts of the code, from the first eigenvector (which is very closely approximate by the above simple form), they calculate a filter for use in obtaining their “nonlinear trend line” as follows (in Matlab code)”

tfilt=conv(E,flipud(E))/M;

Convolving an even vector by another even vector yields a triangular filter which in this case has the form:

(1 2 3 ……M ….. 3 2 1)/M^2

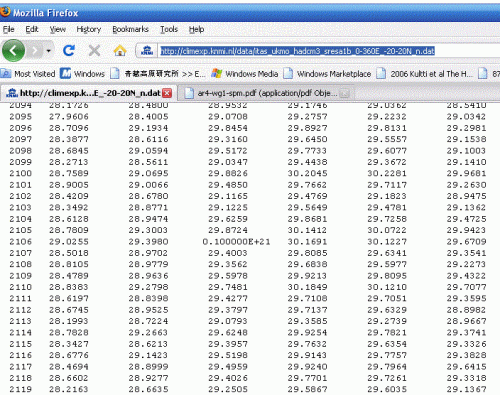
In the figure below, I’ve calculated actual values of the Rahmstorf filter for the HadCRU temperature series with M=11, demonstrating the virtual identity of the Rahmstorf filter with a simple triangular fllter ( \copyright The Team).


Figure 1. Comparison of Triangular and Rahmstorf Filters

In comments at RC and David Stockwell’s, Rahmstorf categorically asserted that they did “not use padding”:

you equate “minimum roughness” with “padding with reflected values”. Indeed such padding would mean that the trend line runs into the last point, which it does not in our graph, and hence you (wrongly) conclude that we did not use minimum roughness. The correct conclusion is that we did not use padding.

Parsing the ssatrend.m code, it turns out that this statement is untrue. The ssatrend algorithm pads with the linear projection using the trend over the last M points – terms like “minimum roughness” seem like rather unhelpful descriptions. Mannian handling of endpoints is a little different – Mann reflected the last M points and flipped them centered on the last point. I observed some time ago (a point noted by David Stockwell in his inquiry to Rahmstorf) that this procedure, when used with a symmetric filter, pinned the smooth on the end-point ( a procedure used in Emanuel’s 2005 hurricane study, but not used when 2006-7 values were low.)

Rahmstorf padding yields results that are a little different from Mannian padding, because the symmetric (very near-)triangular filter applies to actual values in the observed period, but uses linear trend values rather than flipped values in the padding period. If the linear trend “explains” a considerable proportion of the last M points, then, in the padding period, the linear projection values will approximate the flipped values and the smooth from one filter will approximate the smooth from the other filter. Rahmstorf’s statement that he did not use “padding” is manifestly untrue.

Given that the filter is such a simple triangular filter, you can see how the endpoint smoothing works. M years out from the end, it is a triangular filter. But at the last point, in Mannian padding, all the filter terms cancel out except the loading on the last year – hence the end point pinning. The transition of coefficients from the triangular filter to the one-year loading can be calculated in an elementary formula.

Turning now to the underlying reference, Moore et al 2005, I note that EOS is the AGU newsletter and not a statistical journal. [Update note: its webpage states: “Eos is a newspaper, not a research journal.” I receive EOS and often find it interesting, but it is not a statistical journal.]

Given that we now know that the various and sundry operations simply yield a triangular filter, it’s worthwhile re-assessing the breathless prose of “New Tools for Analyzing Time Series Relationships and Trends”.

Moore et al begins:

Remarkable progress recently has been made in the statistical analysis of time series…. This present article highlights several new approaches that are easy to use and that may be of general interest.

Claims that a couple of Arctic scientists had discovered something novel about time series analysis should have alerted the spidey-senses of any scientific reader. They go on:

Extracting trends from data is a key element of many geophysical studies; however, when the best fit is clearly not linear, it can be difficult to evaluate appropriate errors for the trend. Here, a method is suggested of finding a data-adaptive nonlinear trend and its error at any point along the trend. The method has significant advantages over, e.g., low-pass filtering or fitting by polynomial functions in that as the fit is data adaptive, no preconceived functions are forced on the data; the errors associated with the trend are then usually much smaller than individual measurement errors…

The widely used methods of estimating trends are simple linear or polynomial least squares fitting, or low-pass filtering of data followed by extension to data set boundaries by some method [e.g., Mann, 2004]. A new approach makes use of singular spectrum analysis (SSA) [Ghil et al., 2002] to extract a nonlinear trend and, in addition, to find the confidence interval of the nonlinear trend. This gives confidence intervals that are easily calculated and much smaller than for polynomial fitting….

In MC-SSA, lagged copies of the time series are used to define coordinates in a phase space that will approximate the dynamics of the system…

Here, the series is padded so the local trend is preserved (cf. minimum roughness criterion, [Mann, 2004]). The confidence interval of the nonlinear trend is usually much smaller than for a least squares fit, as the data are not forced to fit any specified set of basis functions.

Here’s a figure that probably caught Rahmstorf’s eye. The “new” method had extracted a bigger uptick at the end than they had got using Mannian smoothing. No wonder Rahmstorf grabbed the method. Looking at the details of the caption, the uptick almost certainly arises simply from a difference in filter length.


Fig. 2. Nonlinear trend in global (60°S–60°N) sea surface temperature anomaly relative to 1961–1990 (bold curve) based on the 150- year-long reconstructed sea surface temperature 2° data set (dotted [Smith and Reynolds 2004]), using an embedding dimension equivalent to 30 years; errors are the mean yearly standard errors of the data set. Shading is the 95% confidence interval of the nonlinear trend. The curve was extended to the data boundaries using a variation on the minimum roughness criterion [Mann, 2004]. For comparison the thin curve is the low-pass trend using Mann’s low-pass filter and minimum roughness with a 60-year cutoff frequency.

At the end of the day, the secret of Rahm-smoothing is that it’s a triangular filter with linear padding. All the high-falutin’ talk about “embedding dimension” and “nonlinear … lines” is simply fluff. All the claims about doing something “new” are untrue, as are Rahmstorf’s claims that he did not use “padding”. Rahmstorf’s shift from M=11 to M=15 is merely a shift from one triangular filter to a wider triangular filter – it is not unreasonable to speculate on the motive for the shift, given that there was a material change in the rhetorical appearance of the smoothed series.

Finally, I do not believe that the Team could successful assert a copyright interest in the triangular filter ( \copyright The Team).

By Stephen McIntyre | Posted in General | Tagged | Comments (232)

Increased Atlantic hurricane landfalls from a new form of El Nino?

Jul 2, 2009 – 1:30 PM



Figures: Top: Eastern Pacific Warming (EPW) Atlantic storm tracks for seasons indicated on the plot. EPW is the “traditional El Nino”. Bottom left: Central Pacific Warming (CPW) or the “new” El Nino described in the paper and right: Eastern Pacific Cooling or La Nina. Track legend: [TS,Hurr,Major,Cat5]:[blue,green,red,pink]

A new paper by Kim, Webster, and Curry in Science (2009) has arrived. The paper is accessible to the general reader without training in tropical meteorology or an exhaustive knowledge of the rapidly evolving state of El Nino science.

Abstract:

Two distinctly different forms of tropical Pacific Ocean warming are shown to have substantially different impacts on the frequency and tracks of North Atlantic tropical cyclones. The eastern Pacific warming (EPW) is identical to that of the conventional El Niño, whereas the central Pacific warming (CPW) has maximum temperature anomalies located near the dateline. In contrast to EPW events, CPW episodes are associated with a greater-than-average frequency and increasing landfall potential along the Gulf of Mexico coast and Central America. Differences are shown to be associated with the modulation of vertical wind shear in the main development region forced by differential teleconnection patterns emanating from the Pacific. The CPW is more predictable than the EPW, potentially increasing the predictability of cyclones on seasonal time scales.

Press release:

New type of El Nino could mean more hurricanes make landfall

El Niño years typically result in fewer hurricanes forming in the Atlantic Ocean. But a new study suggests that the form of El Niño may be changing potentially causing not only a greater number of hurricanes than in average years, but also a greater chance of hurricanes making landfall, according to climatologists at the Georgia Institute of Technology. The study appears in the July 3, 2009, edition of the journal Science.

“Normally, El Niño results in diminished hurricanes in the Atlantic, but this new type is resulting in a greater number of hurricanes with greater frequency and more potential to make landfall,” said Peter Webster, professor at Georgia Tech’s School of Earth and Atmospheric Sciences.

That’s because this new type of El Niño, known as El Niño Modoki (from the Japanese meaning “similar, but different”), forms in the Central Pacific, rather than the Eastern Pacific as the typical El Niño event does. Warming in the Central Pacific is associated with a higher storm frequency and a greater potential for making landfall along the Gulf coast and the coast of Central America.

Even though the oceanic circulation pattern of warm water known as El Niño forms in the Pacific, it affects the circulation patterns across the globe, changing the number of hurricanes in the Atlantic. This regular type of El Niño (from the Spanish meaning “little boy” or “Christ child”) is more difficult to forecast, with predictions of the December circulation pattern not coming until May. At first glance, that may seem like plenty of time. However, the summer before El Niño occurs, the storm patterns change, meaning that predictions of El Niño come only one month before the start of hurricane season in June. But El Niño Modoki follows a different prediction pattern.

“This new type of El Niño is more predictable,” said Webster. “We’re not sure why, but this could mean that we get greater warning of hurricanes, probably by a number of months.”

As to why the form of El Niño is changing to El Niño Modoki, that’s not entirely clear yet, said Webster.

“This could be part of a natural oscillation of El Niño,” he said. “Or it could be El Niño’s response to a warming atmosphere. There are hints that the trade winds of the Pacific have become weaker with time and this may lead to the warming occurring further to the west. We need more data before we know for sure.”

In the study, Webster, along with Earth and Atmospheric Sciences Chair Judy Curry and research scientist Hye-Mi Kim used satellite data along with historical tropical storm records and climate models.

The research team is currently looking at La Niña, the cooling of the surface waters in the Eastern and Central Pacific.

“In the past, La Nina has been associated with a greater than average number of North Atlantic hurricanes and La Nina seems to be changing its structure as well,” said Webster. “We’re vitally interested in understanding why El Niño-La Niña has changed. To determine this we need to run a series of numerical experiments with climate models.”

By Ryan Maue | Posted in Hurricane | Tagged , | Comments (112)

Rahmsmoothing and the Canadian GCM

Jul 2, 2009 – 12:17 PM

Quite aside from the realclimatescientistsmoothingalgorithmparameterselectioncontroversy, another interesting aspect of Figure 3 of the Copnhagen Synthesis Report is the cone of model projections. Today I’ll show you how to do a similar comparison for an AR4 model of your choice. Unlike Rahmstorf, I’ll show how this is done, complete with turnkey code. I realize that this is not according to GARP (Generally Accepted Realclimatescientist Procedure), but even realclimatescientists publishing in peerreviewedliterature should be accountable for their methodology.

Here is Figure 3 from the Copenhagen Synthesis Report. I take it that the grey cone is the spread of model prokections – note that the caption says that these are from the Third Assessment Report. Raising the question – why the Third Assessment Report? Wouldn’t the Fourth Assessment Report be more relevant?


Figure 1: Copenhagen Synthesis Figure 3. “Changes in global average surface air temperature (smoothed over 11 years) relative to 1990. The blue line represents data from Hadley Center (UK Meteorological Office); the red line is GISS (NASA Goddard Institute for Space Studies, USA) data. The broken lines are projections from the IPCC Third Assessment Report, with the shading indicating the uncertainties around the projections3 (data from 2007 and 2008 added by Rahmstorf, S.).”

The IPCC AR4 Smear Graph
In April 2008, doctorrealclimatescientist Rahmstorf discussed models versus observation, excerpting IPCC Figure 1.1 which showed both the AR4 cone and the Tar cone as shown below. As I understand it, these cones are more or less spaghetti graphs with one color – grey.


Figure 2. IPCC Figure 1.1 shown by Rahmstorf at RC in April 2008.

The Canadian GCM
I thought that it would be interesting to do my own comparison from first principles. Rather than smearing everything into one big stew a la IPCC, I thought that it would be interesting to show results for individual models. And to simplify presentation, I’m only showing HadCRU, rather than spaghetti-ing it up with GISS. In making this presentation, I used my implementation in R of ssatrend (benchmarked against the original Matlab version – more on this later.) I also used my function to scrape model data from KNMI (this function constructs CGI commands at KNMI within R.)

Here’s a Rahmstorf-style plot for the Canadian GCM runs, chosen because I’m Canadian. (Actually I knew from Santer studies that it runs “hot”, so it wasn’t entirely a random selection. I wanted to see what this sort of model looked like.) I’ve only examined these plots for a few models – NCAR is another one that I looked at- but I can modify the script easily to make a pdf showing similar plots for all models and might do this some time.

I invite readers to consider whether there is a “remarkable similarity” between the geometry of the coherence of model and observations in this graphic and the coherence of model and observations in the Copenhagen Synthesis graphic. One noticeable difference between this graphic and the realclimatescientistgraphic is that it does not truncate the hindcast performance. In this case, one is inclined to say that the proprietors of this particular model haven’t gone out of their way to tune its performance to actual 20th century history. I’m pretty sure that this model is at the upper sensitivity end, but I don’t know this.


Comparison of Canadian CCCMA to HadCRU, in Rahmstorf 2007 style.

Readers may easily derive this graphic for themselves using the following turnkey code. First load functions to implement KNMI scrape and Rahmstorf smoothing and plotting:

source(“http://data.climateaudit.org/scripts/models/functions.collation.knmi.txt”)
#function to scrape from KNMI
source(“http://data.climateaudit.org/scripts/rahmstorf/functions.rahmstorf.txt”)
#emulation of Rahmstorf smooth

Now load HadCRUT3v and Rahmsmooth it, using the realclimatescientistsmoothingparameter of Rahmstorf et al 2007.

source(“http://data.climateaudit.org/scripts/spaghetti/hadcru3v.glb.txt”) #hadcru3v, hadcru3v.ann
had=hadcru3v.ann
had_smooth= ssatrend(window(had,end=2008),M=11) #Rahmsmooth

Make sure that you register at KNMI. Then insert your registered email address in the R-code as shown below

email=Email= [##register and insert your email here

Now logon and set the field to “tas” (temperature at surface) and the scenario to A1B “sresa1b”. The code below will print out the available KNMI models according to a semi-manual collation from their webpage a few months ago. (KNMI needs to have a readable list of models !!)

logon=download_html( paste(“http://climexp.knmi.nl/start.cgi?”,Email,sep=””))
scenario=”sresa1b”
field=”tas”;
Info=knmi.info[knmi.info$scenario==scenario,]
row.names(Info)=1:nrow(Info)
Info #gives A1B models at KNMI

To generate the CCCMA figure in this post, look up their row-number of the model in the Info table generated above and simply execute the following command. This should scrape the data from KNMI. If it doesn’t, then there;s probably something wrong with your KNMI handshake.

plotf(2) #CCCMA

Just change the number to generate other model comparisons. (I’ll use the pdf function to generate all the models in one document.)

Update: I modified the function a little and produced a pdf with all the models plotted in the above style. A pdf is at http://www.climateaudit.org/data/models/models_vs_hadcru.pdf . Virtually every model performed better than the Canadian GCM.

pdf(file=”d:/climate/images/2009/models/models_vs_hadcru.pdf”,width=5,height=5)
for (i in 1:nrow(Info)) plotf(i,gdd=FALSE) #CCCMA
dev.off()

By Stephen McIntyre | Posted in Modeling | Tagged | Comments (35)

Opportunism and the Models

Jul 1, 2009 – 10:41 PM

Many CA readers have probably been checking out some interesting post at Lucia’s about Stefan Rahmstorf’s opportunistic smoothing of temperature observations in Copenhagen. See here here and here at Lucia’s. Also see David Stockwell’s recent post here and his recent E&E paper on Rahmstorf et al (Science 2007) (Rahmstorf here). Also see the recent Copenhagen Synthesis Report here.
[Update – Jul 2] David Stockwell had an excellent comment on this issue in April 2008 here – see Rahmstorf comment at #14 (thanks to PaulM for drawing this to my attention).

Rahmstorf, a realclimatescientist (a literal translation of the compound German noun), stated in Rahmstorf et al 2007 that the trends were worse than we thought:

The data now available raise concerns that the climate system, in particular sea level, may be responding more quickly than climate models indicate… The global mean surface temperature increase (land and ocean combined) in both the NASA GISS data set and the Hadley Centre/Climatic Research Unit data set is 0.33°C for the 16 years since 1990, which is in the upper part of the range projected by the IPCC.

This was illustrated with the following figure, which has a couple of interesting features. First, the method of smoothing is described only as follows: “All trends are nonlinear trend lines and are computed with an embedding period of 11 years.”


Figure 1. Excerpt from Rahmstorf et al 2007. “All trends are nonlinear trend lines and are computed with an embedding period of 11 years.”

Commenters at Lucia’s and David’s state that Rahmstorf refused to disclose his smoothing method (which proved ultimately to be a sort of Mannian smoothing) on the basis that he did not hold the copyright. Eventually Jean S figured it out and his method was used in David Stockwell’s E&E paper. David has an R-port of the method online (using an R-package ssa presently unavailable for Windows).

Secondly, Rahmstorf has zeroed both models and observations on 1990. I recall some controversy about Willis Eschenbach zeroing GISS models on 1958; I have a vague recollection of Hansen’s dogs saying that this was WRONG. I don’t vouch for this recollection, but, if the events were as I vaguely recall, I don’t see any material difference in Rahmstorf’s centering here.

In David Stockwell’s E&E article, he observed that Rahmstorf’s method applied to updated GISS and CRU resulted in the smooth tapering off. See the online article for the following image. Obviously the tapering off diminishes the rhetorical impact considerably.


Figure 2. Stockwell’s extension of R2007 using the same methodology.

The new Copenhagen Report has an update of the Rahmstorf 2007 diagram (Rahmstorf is said to have added 2007 and 2008 data). The data is said to be smoothed over 11 years (as in Rahmstorf 2007):

Changes in global average surface air temperature (smoothed over 11 years) relative to 1990. The blue line represents data from Hadley Center (UK Meteorological Office); the red line is GISS (NASA Goddard Institute for Space Studies, USA) data… (data from 2007 and 2008
added by Rahmstorf, S.)

However, the Copenhagen diagram doesn’t taper off – a highly important difference in rhetorical effect from the updated version of the Rahmstorf diagram published by David Stockwell.

Figure 3. Rahmstorf’s extension – note the lack of taper occurring in the Stockwell version.

Jean S once again figured this out – Rahmstorf opportunistically changed the smoothing parameter to one that yielded an image that was rhetorically more effective and failed to disclose the change in accounting procedure, falsely reporting that he used the same parameter as in the prior article. This is what the “Community” calls “GARP” – Generally Accepted Realclimate Procedure.

I’ve done a few experiments comparing AR4 A1B models to updated CRU data. More on this tomorrow. I’ve done my own port of Rahmstorfian smoothing to R without using the ssa package – working from first principles. It uses nothing more complicated than svd and a quasi-Mannian padding. (Rahmstorf’s “copyright” pretext is absurd BTW. The Community really has to tell the Team to stop such nonsense.)

By Stephen McIntyre | Posted in Modeling | Comments (46)

Hurricane watch 2009: scraping the bottom

Jun 29, 2009 – 11:03 PM

With the North Atlantic hurricane season still waiting for a named storm, and the rest of the globe cyclonically challenged during the past several months, it is a good time to catch up on the research end of things. In terms of papers during the past 6-8 months, the amount of tropical cyclone and climate literature has largely dropped off compared to the heyday after Katrina. Regardless, the following is an “omnibus” style blog posting and can serve as the obligatory 2009 Atlantic Hurricanes posting.

First, the forecasts for the upcoming Atlantic hurricane season are decidedly below-normal or below median or less-active depending upon the metric or audience. The UK Met Office, which recently had its climate research budget slashed 25%, has determined the most likely amount of storms is 6, very low compared to what has been seen since the active period in the Atlantic began in 1995. The most likely Accumulated Cyclone Energy (ACE) tally is predicted to be 60, which is in the basement compared to recent seasons.

Here is a helpful comparison of previous seasons of ACE that I plotted up from the HURDAT best-track dataset maintained by the friendly folks at the hurricane center and NOAA.


Figure: The ACE from 1935-2008 for the North Atlantic with the Met Office prediction as the squat, little red bar.

NOAA and Bill Gray’s CSU forecasting outfit are in close agreement:

NOAA: 9-14 named storms (including Baby Whirls), 4-7 hurricanes (1-3 major) and ACE of about 65-125. The ranges are rather large with NOAA forecasts, and the previous 5-6 years’ forecasts have an uncanny resemblance to each other; they are essentially the same forecast year after year.

Gray and Dr. Phil Klotzbach (CSU, June 2 update): 11 named storms, 5 hurricanes (2-major), and an ACE of 85.

Here is a flavoring of the latter’s reasoning:

We expect current neutral ENSO conditions to persist or perhaps transition to weak El Niño conditions by the most active portion of this year’s hurricane season (August-October). If El Niño conditions develop, it would tend to increase the levels of vertical wind shear and decrease the levels of Atlantic hurricane activity. Another reason for our forecast reduction is due to the persistence of anomalously cool sea surface temperatures in the tropical Atlantic. Cooler waters are associated with dynamic and thermodynamic factors that are less conducive for an active Atlantic hurricane season. Another factor in our forecast reduction is the stronger-than-normal Azores High during April-May. Stronger high pressure typically results in stronger trade winds that are commonly associated with less active hurricane seasons.

Secondly, Global tropical cyclone activity (or hurricane, typhoon, cyclone) has continued to plummet to levels now approaching 50-year lows. There is no mystery why this is occurring: it is entirely natural and associated strongly with the fluctuations of large-scale climate including the well-known El Nino – Southern Oscillation. The extended and powerful La Nina period beginning in 2007 precipitated the downturn in global TC activity as measured by ACE. One ENSO index called the MEI highlights the recent strong La Nina and the last few months tick up to more neutral/warm conditions.

Now, when you take a gander at the global ACE using a 24-month running sum, it is rather apparent that there is a strong relationship. Why do I use a 24-month running sum? The time scale of El Nino events is typically 2-7 years, and more importantly, the Southern Hemisphere tropical season peaks in boreal winter. Thus, if you use calendar year January-December metrics, you necessarily chop off or alias the seasonal activity into unrealistic combinations. Thus, the 24-month sums are smoother but no data is removed, it is raw. Additional details are at my FSU website and a recent GRL article I published in March 2009: Northern Hemisphere Tropical Cyclone Activity.

The current global TC ACE number valid for July 1, 2009 summing the previous 24-months is 1083, and the Northern Hemisphere number is 802. For the calendar year 2009, Northern Hemisphere (NH) ACE is at 33 which is at about 50% of the previous 30-year average. This is not unusual as some Western Pacific typhoon and Eastern Pacific hurricane seasons don’t ramp up until mid- to late-July. However, this is little reason to believe above average NH for 2009 is in the cards.

A discerning eye will see that there is no trend in the Northern Hemisphere ACE during the past 50-years even considering that there is a void of Eastern Pacific and Northern Indian Ocean data prior to about 1970. The global data prior to 1970 also suffers from poor intensity estimates in the Southern Hemisphere when/where satellite observations were very limited. Interestingly, one satellite image was from 40-years ago from the Apollo moon-landing (the Lost Tapes have been found!).

Thirdly, the Copenhagen Synthesis Report received laudatory coverage in the media.

The world faces a growing risk of “abrupt and irreversible climatic shifts” as fallout from global warming hits faster than expected, according to research by international scientists released Thursday.
Global surface and ocean temperatures, sea levels, extreme climate events, and the retreat of Arctic sea ice have all significantly picked up more pace than experts predicted only a couple of years ago.

If you sift through the report, you find Figure 6 on page 12 referencing a talk given by Greg Holland on Atlantic hurricane activity.


Figure 6: (A) The numbers of North Atlantic tropical cyclones for each maximum wind speed shown on the horizontal axis. The most intense (Category 5) tropical cyclones have maximum wind speeds of 70 m/s or greater. (B) The proportional increase by cyclone (hurricane) category (1 – least intense; 5 – most intense) arising from increases in maximum wind speeds of 1, 3 and 5 m/s. Note the disproportionately large increase in the most intense tropical cyclones with modest increases in maximum wind speed, compared to the increase in less intense cyclones (23).

After a little digging, reference number 23 points to the talk Dr. Holland gave in Copenhagen back in March, right before Roger Pielke. Here is the extended PDF document.

Figure 1 of the extended abstract shows the maximum intensity distribution of Atlantic tropical cyclones for the period of 1945-2007. He states that theory suggests a potential 1-5 m/s increase in hurricane intensity for a concomitant increase of 1 degree C in ocean temperatures. Quoting: “The impact of a uniform 1, 3 and 5 ms-1 increase in these intensities is shown in Fig. 1b. Quite modest changes of < 20% are indicated for category 1-3 and even category 4 hurricanes. These changes are small compared to interannual variability and would be difficult to detect. But the most intense, category 5 hurricanes could experience an amplified response, doubling in number for a general 5 m/s increase."

Where does Figure 1b come from? It is simply moving the PDF to the right, apparently the tail is a function of the mean. Anyone have an issue with doing that? Just warming up. Figure 2 shows observational proof of this previous hypothesis:

Whoa! Category 5’s have increased by 300-400%! Holland goes on:

Although this example has only considered Atlantic hurricanes, we suggest that the overall result is robust and applicable more widely to weather extremes. Major difficulties arise from the relative rarity and patchy nature of weather extremes and from the inability of current climate models to simulate them.

This seemingly is the converse to the Baby Whirl detection issue brought up here at Climate Audit. The discovery of Category 5 hurricanes in the past is likely a function of our detection capabilities which have markedly improved during the past several decades. Thus, as with Baby Whirls, plotting up Category 5’s as detection has improved apparently will give you hockey stick looking graphs.

Holland points out that changes in the tracks of hurricanes may lead to more Category 5’s, which he alleges are climate signals. Unfortunately, there is no breakdown of natural variability versus climate change / global warming presented. Instead, we are urged to consult the “purely statistical reasoning” in Figure 1, which “implies that other physical factors are contributing to a skewing of the distribution”.

I do not buy the assumption that the PDF of maximum hurricane intensity will simply shift to the right, and I do not find the analysis a “tentative confirmation of (Holland’s) hypothesis.” Furthermore, this analysis is not yet in the peer-reviewed literature.

Lastly, as entertainment value, the Weather Channel on June 30th is going to focus on the “skill” of “hot models” (not Maxim but HWRF) with regards to hurricane forecasting. One such HWRF forecast run of invest 93L in the Caribbean was really out to lunch. Here is the landfall location and an animation to the model run. To be fair, HWRF is “experimental” but it is astounding that it can be so wrong. A trained forecaster would immediately discount this run.
Note: This is NOT a current forecast. The circulation never developed into a tropical storm.

Horribly blown forecast animation for June 27, 2009 00Z forecast.

Couldn’t think of a better selling point for Congressman Alan Grayson (D) and his proposed $50 million U Central Florida / Obama Hurricane Center in Orlando FL, which was added as a Christmas tree ornament in the climate change bill passed by the House of Reps late Friday.

Congressman Grayson said, “With this one move, Central Florida will become a world leader in 21st century meteorology.”

By Ryan Maue | Posted in Hurricane | Comments (238)

Names That Cannot Be Said

Jun 29, 2009 – 10:16 PM

Continuing the petty practice of refusing to cite HS critics, Johann h. Jungclaus, writing in Nature Geoscience, “Lessons from the past millennium”, discusses the “debate about the ‘hockey-stick’ curve” without citing the critical MM articles:

Knowledge of past climate evolution is essential for understanding natural climate variability. The debate about the ‘hockey-stick’ curve — a reconstruction of Northern Hemisphere temperatures over the past millennium[1 – MBH]— revolved around the extent to which recent climate warming is unprecedented in a longer-term context. The controversy calmed down after several reassessments [2 – IPCC AR4, 3 – NAS Panel] that confirmed the unique magnitude of warming since the late twentieth century, but the amplitude of multi-centennial temperature changes over the past millennium is still not well understood.

As CA readers realize, all that 2 and 3 confirmed is that Graybill bristlecone chronologies have a unique uptick in the 20th century, but that is of no interest to the “Community”.

By Stephen McIntyre | Posted in General | Comments (16)

Orland CA and the New Adjustments

Jun 29, 2009 – 8:24 PM

In my last post, I observed that NOAA’s Talking Points applied their new “adjustments” to supposedly prove that NOAA’s negligent administration of the USHCN network did not “matter”.
In order to illustrate the effect of the new methods in this post, I’ll compare the new adjustments (post-TOBS) to the old adjustments (post-TOBS) on a “good” station – Orland CA, a prototype “good” station, discussed at the outset of surfacestations.org, discussed at WUWT here and CA here in early 2007.

The station history for Orland (at CDIAC) says that it has been in its present location for (at least) most of the 20th century and has had minimal changes during that time, other than perhaps time-of-observation (TOBS). The TOBS adjustment is carried forward into USHCN-v2. As I understand it, NOAA’s New Adjustment Method replaces station-history based adjustments for instrumentation changes and station location (the latter formerly done in FILNET).

As a benchmark, here is the difference between FILNET (adjusted) and TOBS for Orland in the “old” USHCN. Adjustments in the 20th century are negligible – in keeping with station history information that indicates no changes in location.


Figure 1. “Old” USHCN Adjustments for Station Location and Instrument Changes

Now here is the net adjustment in the “New” USHCN.

Two points jump out. Look first at the monthly adjustments at the right hand side. In the “old” method, there weren’t any adjustments to recent data – where metadata did not indicate any relevant change. In the “new” method, there are all sorts of jittery little adjustments. They seem to average out, but why introduce these jitters in the first place? It’s starting to look like a pointless Hansen-esque (ROW-style) adjustment that simply distorts the underlying data.

On a larger scale, the new adjustment noticeably increases the 20th century trend at Orland.

These graphics strongly indicate to me that the effect of the algorithm – regardless of whatever good intentions may underlie it – is that data from lower quality stations is being blended into the presently archived Orland data. I presume that something similar is happening to other “good” stations (though I’ve only examined one example so far.) (Note that Orland is a CRN3 station. However, its excellent continuity makes it a pretty attractive station for benchmarking and visually it doesn’t look a “bad” CRN3 station).

Based on this example, it looks like NOAA’s Talking Points comparison is between the overall average and 70 “adjusted” stations – AFTER the good stations have been adjusted. 🙂

By Stephen McIntyre | Posted in Surface Record | Tagged , | Comments (26)

The Talking Points Memo

Jun 29, 2009 – 7:32 AM

The NOAA Talking Points memo falls well short of a “full, true and plain disclosure” standard – aside from the failure to appropriately credit Watts (2009).

They presented the following graphic that purported to show that NOAA’s negligent administration of the USHCN station network did not “matter”, describing the stations as follows:

Two national time series were made using the same gridding and area averaging technique. One analysis was for the full data set. The other used only the 70 stations that surfacestations.org classified as good or best… the two time series, shown below as both annual data and smooth data, are remarkably similar. Clearly there is no indication for this analysis that poor current siting is imparting a bias in the U.S. temperature trends.


Figure 1. From Talking Points Memo.

Beyond the above sentence, there was no further information on the provenance of the two data sets. NOAA did not archive either data set nor provide source code for reconciliation.

The red graphic for the “full data set” had, using the preferred terminology of climate science, a “remarkable similarity” to the NOAA 48 data set that I’d previously compared to the corresponding GISS data set here (which showed a strong trend of NOAA relative to GISS). Here’s a replot of that data – there are some key telltales evidencing that this has a common provenance to the red series in the Talking Points graphic.


Figure 2. Plot of US data from http://www1.ncdc.noaa.gov/pub/data/cirs/drd964x.tmpst.txt

An obvious question is whether the Talking Points starting point of 1950 is relevant. Here’s the corresponding graphic with the 1895 starting point used in USHCN v2. Has the truncation of the graphic start at 1950 “enhanced” the visual impression of an increasing trend? I think so.


Figure 3. As Figure 2, but to USHCN v2 start

The Talking Points’ main point is its purported demonstration that UHI-type impacts don’t “matter”. To show one flaw in their arm-waving, here is a comparison of the NOAA U.S. temperature data set and the NASA GISS US temperature data set over the same period – a comparison that I’ve made on several occasions, including most recently here. NASA GISS adjusts US temperatures for UHI using nightlights information, coercing the low-frequency data to the higher-quality stations. The trend difference between NOAA and NASA GISS is approximately 0.7 deg F/century in the 1950-2008 period in question: obviously not a small proportion of the total reported increase.


Figure 4. Difference between NOAA and NASA in the 1950-2008 period. In def F following NOAA (rather than deg C)

As has been discussed at considerable length, the NASA GISS adjusted version runs fairly close to “good” CRN1-2 stations – a point which Team superfans have used in a bait-and-switch to supposedly vindicate entirely different NASA GISS adjustments in the ROW, (adjustments which appear to me to be no more than random permutations of the data, a point discussed at considerable length on other occasions.)

For present purposes, we need only focus on the observation that there is a substantial trend difference between NOAA and GISS trends.

Given that, when NOAA’s Talking Points claim that there is a supposedly negligible difference between the average of their “good” stations and the NOAA average (which we know to run hot relative to GISS), then arguably this raises issues about the new USHCN procedures.

Y’see, while NOAA doesn’t actually bother saying how it did the calculations, here’s my guess as to what they did. The new USHCN data sets (as I’ll discuss in a future post) ONLY show adjusted data. No more inconvenient data trails with unadjusted and TOBS versions.

When I looked at SHAP and FILNET adjustments a couple of years ago, one of my principal objections to these methods was that they adjusted “good” stations. After FILNET adjustment, stations looked a lot more similar than they did before. I’ll bet that the new USHCN adjustments have a similar effect and that the Talking Points memo compares adjusted versions of “good” stations to the overall average.

So what they are probably saying is this: after the new USHCN “adjustments” (about which little is known as the ink is barely dry on the journal article describing the new method and code for which is unavailable), there isn’t much difference between the average of good stations and the average of all stations.

If the NASA GISS adjustment procedure in the US is justified (and most Team advocates have supported the NASA GISS adjustment in the US), then the Talking Points memo merely demonstrates that there is something wrong with the new USHCN adjustments.

By Stephen McIntyre | Posted in Surface Record | Tagged , , , | Comments (73)

USHCN V2 Deletions and Additions

Jun 28, 2009 – 10:30 PM

Menne et al (J Clim 2009) reported that there were 62 station deletions and 59 station additions from the most recent roster (which itself had been modified from the original USHCN in the mid-1980s. Menne et al:

Since the 1996 release (Easterling et al. 1996), numerous station closures and relocations again necessitated a revision of the network. As a result, HCN version 2 contains 1218 stations, 208 of which are composites; relative to the 1996 release, there have been 62 station deletions and 59 additions.

I’ve provided a list of deleted and added stations below. I looked up one of the stations (the last one on the list, WY Pathfinder Dam, surfacestations.org. It was surveyed in June 2008, at which time it still existed. It doesn’t look bad as compared to the Tucson parking lot (which is still used.)

What is the basis for deleting one station and adding another? Dunno. They say that it’s due to “numerous station closures and relocations”, but there seem to be examples where this is untrue.


Figure 1. Pathfinder Dam WY.

Here’s a list of the 61 deleted sites (by state):
[1] “AZ DOUGLAS” “AZ MESA” “AR OZARK” “CO DURANGO”
[5] “GA BLAKELY” “ID CALDWELL” “ID CHALLIS” “ID COEUR D’ALENE AP”
[9] “IL GRIGGSVILLE” “KS ESKRIDGE 1SE” “KS PHILLIPSBURG 1SSE” “KY MIDDLESBORO”
[13] “KY OWENSBORO 3W” “ME ORONO” “ME RIPOGENUS DAM” “MD BALTIMORE WSO CITY”
[17] “MD COLLEGE PARK” “MD PATUXENT RIVER” “MA CHESTNUT HILL” “MA CLINTON”
[21] “MA FRAMINGHAM” “MN HALLOCK” “MN POKEGAMA DAM” “MN WINNIBIGOSHISH DAM”
[25] “MT CROW AGENCY” “MT HAUGAN (DEBORGIA) 3E” “MT POPLAR” “NE HALSEY 2W”
[29] “NH BETHLEHEM” “NJ TUCKERTON” “NY BAINBRIDGE 2E” “NY BATH”
[33] “NY CHASM FALLS” “NY PENN YAN 8W” “NY PLATTSBURGH AFB” “NY SCARSDALE”
[37] “NY UTICA” “NC BANNER ELK” “ND MAYVILLE” “OH NAPOLEON”
[41] “OK HUGO” “OR BLY 3NW” “PA FREELAND” “PA HARRISBURG CAPITAL CITY”
[45] “UT BEAVER” “UT ELBERTA” “UT HIAWATHA” “UT LOA”
[49] “UT RIVERDALE” “VT NORTHFIELD 3SSE” “WA COLFAX 1NW” “WA COLVILLE 5NE”
[53] “WA GOLDENDALE” “WA GRAPEVIEW 3SW” “WA PUYALLUP EXPERIMENT STN 2W” “WV GARY”
[57] “WV PICKENS 4SSE” “WV WILLIAMSON” “WI HATFIELD HYDRO PLANT” “WY BORDER 3N”
[61] “WY BUFFALO BILL DAM” “WY PATHFINDER DAM”

Here are the 58 added sites:
[1] “AZ CHANDLER HEIGHTS” “AZ PEARCE SUNSITES” “AR OZARK 2” “GA CAMILLA 3SE”
[5] “ID BERN” “ID COEUR D’ALENE” “ID MAY 2 SSE” “ID NAMPA SUGAR FACTORY”
[9] “IL PERRY 6 NW” “KS COUNCIL GROVE LAKE” “KS SMITH CENTER” “KY BARBOURVILLE”
[13] “KY HENDERSON 7 SSW” “ME BRASSUA DAM” “ME CORINNA” “MD BELTSVILLE”
[17] “MD BALTIMORE DOWNTOWN” “MA READING” “MA WALPOLE 2” “MA WEST MEDWAY”
[21] “MN RGYLE 4 E” “MN GRAND RAPIDS FORESTRY LAB” “MN MARCELL 5 NE” “MT HYSHAM 25 SSE”
[25] “MT SAINT REGIS 1 NE” “MT VIDA” “NE STAPLETON” “NH BETHLEHEM 2”
[29] “NJ TOMS RIVER” “NM ULCE” “NY ADDISON” “NY DEPOSIT”
[33] “NY DOBBS FERRY ARDSLEY” “NY MALONE” “NY UTICA ONEIDA COUNTY AIRPORT” “NC TRANSOU”
[37] “ND CASSELTON AGRONOMY FARM” “OH DEFIANCE” “PA LEBANON 2 W” “PA PLEASANT MOUNT 1 W”
[41] “TX PARIS” “UT FARMINGTON 3 NW” “UT MARYSVALE” “UT NEPHI”
[45] “UT SALINA 24 E” “UT SCOFIELD-SKYLAND MINE” “VT OUTH HERO” “VT SOUTH LINCOLN”
[49] “WA COLVILLE” “WA CUSHMAN POWERHOUSE 2” “WA GOLDENDALE” “WA McMILLIN RESERVIOR”
[53] “WA SAINT JOHN” “WV PICKENS 2 N” “WV PINEVILLE” “WV WILLIAMSON”
[57] “WI NEILLSVILLE 3SW” “WY BATES CREEK NO 2” “WY CODY”

Reference:
Menne et al, 2009. The United States Historical Climatology Network Monthly Temperature Data – Version 2. J Climate. http://ams.allenpress.com/perlserv/?request=get-abstract&doi=10.1175%2F2008BAMS2613.1

By Stephen McIntyre | Posted in General | Tagged , | Comments (20)