Here’s a first attempt at applying the techniques of Brown and Sundberg 1987 to MBH99. The results shown here are very experimental, as I’m learning the techniques, but the results appear very intriguing and to hold some possibility for linking temperature reconstructions to known statistical methodologies – something that seems more scientifically useful than “PR Challenges” and such indulgences. Ammann and the rest of the Team are lucky to be able to mainline grants from NOAA, NSF etc for such foolishness.
One of the strengths of Brown’s approach is to provide some tools for analyzing inconsistency between proxies. This has been an issue that we’ve discussed here on an empirical basis on many occasions. Let’s suppose that you have a situation where your “proxies” are somewhat coherent in the instrumental period (say 1856 on), but are inconsistent in their earlier history – a possibility that can hardly be dismissed out of hand. And you can analyze your data in the instrumental period till you’re blue in the face – you can call part of it “calibration” and part of it “verification”, but it still won’t prove anything about potential inconsistency in earlier periods. You have to have some way of measuring and analyzing potential inconsistency in the earlier periods – even if you don’t have instrumental information to calibrate against.
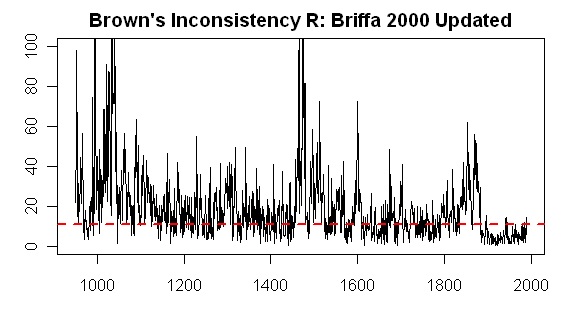
Brown’s “Inconsistency R” (which I’ll call Inconsistency Rb” here) to try to avoid confusion with 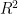 is one way of doing so. To motivate interest in details of this statistic, the figure below shows the Inconsistency Rb for the MBH99 network (14 series). Brown and Sundberg 1989 (p 352) says that this statistic has a chi-squared distribution with q-p degrees of freedom (here 14-1=13); the red line shows the 95% percentile value of this statistic (a benchmark used in Brown’s publications.
is one way of doing so. To motivate interest in details of this statistic, the figure below shows the Inconsistency Rb for the MBH99 network (14 series). Brown and Sundberg 1989 (p 352) says that this statistic has a chi-squared distribution with q-p degrees of freedom (here 14-1=13); the red line shows the 95% percentile value of this statistic (a benchmark used in Brown’s publications.
In my opinion, this is a very dramatic graph and should give pause even to the PR consultants and challengers hired by NOAA and NSF. There is obviously a very dramatic decrease in the Inconsistency Rb statistic in the instrumental period and particularly in the calibration period. This is a vivid quantification of something that we’ve observed empirically on many occasions. This change begs for an explanation, to say the least. This graphic raises two different and important questions: 1) what accounts for the change in inconsistency R statistic during the instrumental period relative to the pre-instrumental period? 2) what do the very high inconsistency R values in the pre-instrumental period imply for confidence intervals?
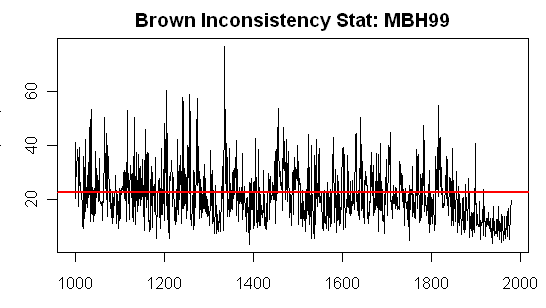
Figure 1. Brown’s Inconsistency Rb Statistic for MBH99 Network (14 series).
For the first question, the change in Inconsistency Rb levels from the pre-instrumental to instrumental period, one hypothetical explanation would be that the changes in the instrumental period are “unprecedented” and that this has occasioned unprecedented coherence in the proxies. An alternative explanation is that the “proxies” aren’t really proxies in the sense of being connected to temperature by a relationship and that the reduced inconsistency in the calibration period is an artifact of cherrypicking, not necessarily by any one individual, but by the industry.
Interesting as this question may be (and I don’t want a whole lot of piling on and venting about this issue which has been amply discussed), I think that we can circumvent such discussions by looking at the 2nd question: the calculation of likelihood-based confidence intervals in the period where there is a high Inconsistency R statistic.
High levels of the Inconsistency R statistic mean that the information from the “proxies” is so inconsistent that the 95% confidence interval is so wide as to be uninformative. The graphic below shows a plot in the style of Brown and Sundberg 1987 showing likelihood based 95% confidence intervals for three years, selected to show different Inconsistency Rb statistic levels.
The highest value of Inconsistency Rb was in 1133, where the Inconsistency stat exceeds 50. The “proxies” are very inconsistent and a likelihood-based confidence calculation from the MBH proxies tells us only that there is a 95% chance that the temperature (in anomaly deg C basis 1902-1980) was between -20 deg C and 20 deg C., a result that seems highly plausible, but uninformative. By comparison, the MBH99 confidence interval (the basis of which remains unknown despite considerable effort to figure it out by UC, Jean S and myself) was 0.96 deg C.
The year 1404 had an Inconsistency R of 26.6, slightly above the 95% chi-squared value for inconsistency. The Brown-style confidence interval was 2.2 deg C, as compared to MBH99 CI of 0.98 deg C (again using an unknown method) and an MBH98 CI of 0.59 deg C (based on calibration period residuals).

The graphic below compares confidence intervals calculated in the Brown-Sundberg 1987 style to those reported in MBH99 (red) and MBH98 (green). Note the similarity in shape between the CI widths here and the Inconsistency Rb statistic (a similarity which is more pronounced between the log(CI) and the Inconsistency statistic, which are related.

Calculation of the Inconsistency R Statistic
The underlying assumption for these calculations if that there is a statistical relationship between proxies (Y) and temperature (X) can be modelled. Yeah, yeah, I know all the arguments about tree rings (of all people in the world, I don’t need readers to remind me that these relationships are precarious), but mathematically one can carry out calculations as if there was a relationship – just as one does in mathematics arguments even if one’s objective is to show a contradiction. The model is simply:
(1) 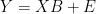 where the errors E have some sort of structure.
where the errors E have some sort of structure.
What’s important here is that the model is from cause (X-temperature) to effect (Y – tree rings etc), something that is not always observed in Team methodologies and that there are residuals from this model for each proxy providing a lot of information about the model that is not used by the Team (“thrown away” perhaps).
The matrix of regression coefficients  , which I usually denote simply as
, which I usually denote simply as  to simplify notation but it’s important to keep track of this, is calculated (for now) using garden variety OLS methods. In my calculations, everything’s been centered in the calibration period. This is OK for regression, though not a good idea for principal components. The matrix denoted here by
to simplify notation but it’s important to keep track of this, is calculated (for now) using garden variety OLS methods. In my calculations, everything’s been centered in the calibration period. This is OK for regression, though not a good idea for principal components. The matrix denoted here by  consistent with Brown’s notation is Mann’s
consistent with Brown’s notation is Mann’s 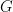 . Thus,
. Thus,
(2) 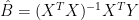
This fit in the calibration period yields a matrix of calibration period residuals 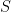 . This is very important for statistical analysis as this matrix of residuals
. This is very important for statistical analysis as this matrix of residuals 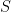 is a workhorse in analysis by statistical professionals. (By contrast, I’ve never seen this object analyzed or mentioned even once in any Team publication!) Brown divides
is a workhorse in analysis by statistical professionals. (By contrast, I’ve never seen this object analyzed or mentioned even once in any Team publication!) Brown divides 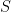 by (n-p-q) to define his
by (n-p-q) to define his  as follows (his equation 2.11):
as follows (his equation 2.11):
(3) 
He then calculates the garden variety GLS estimate (as follows where y is a vector representing proxy values in one year):
(4) 
This yields a vector of GLS-estimated proxy values 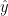 given the calibration model and the GLS-temperature estimate
given the calibration model and the GLS-temperature estimate 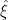 calculated in the usual way:
calculated in the usual way:
(5) 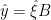
and defines the inconsistency R (a scalar) from the residuals:
(6) 
UC has consistently emphasized the similarity of MBH methodology to “Classical Calibration” other than its idiosyncratic ignoring of the residual matrix and its ultimately arbitrary re-scaling of series to make them “fit” – a procedure that is then said in climate literature to be “correct”, although the only authority for the “correctness” of the procedure would be appear to be Mann himself, a nuance which doesn’t appear to “matter” to IPCC – and UC has been very consistent in objecting to this procedure.
What’s important for readers here about this statistic is that it’s relevant to the temperature reconstruction issues discussed here and that a statistical authority has derived a distribution for this statistic and has used it to consider problems not dissimilar to ones that interest us. For example, Brown and Sundberg ponder questions like whether the calibration model is still applicable in the prediction period, or whether, heaven forbid, new data and new measurements are needed.
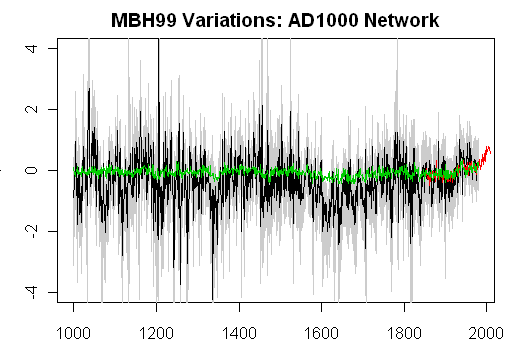
In this case, the MBH Inconsistency statistics are in the red zone from the early 19th century to earlier periods, suggesting that this particular network (the AD1000 network) is not usable prior to the early 19th century. The reason why the MBH results are unstable to seemingly slight methodological variations (e.g. Bürger and Cubasch) is because the individual series are inconsistent. Any PR Challenge analyses which purport to replicate “real world” proxy behavior of MBH type have to have this sort of inconsistency, something that is not done in standard climate pseudoproxy studies, where the mere addition of standard amounts of white or low order red noise, still leaves data that would be “consistent” according to this statistic.
Oh, and what do the “reconstructions” themselves look like done this way? The figure below shows the maximum likelihood reconstruction (black), confidence intervals (light grey) together with the CRU NH instrumental red and the MBH reconstruction (here an emulation of the AD1000 network using the WA variation (green), the WA variation being separately benchmarked to be 100% file-compatible with Wahl and Ammann in the AD1400 network).
A closing comment about continuing to use MBH networks for statistical analysis. It is very common in statistical literature to use rather archaic but familiar data sets to benchmark and compare methods. The paint data of Brown 1982 has no intrinsic interest, but has been considered in a number of subsequent multivariate studies. This sort of thing is very common in statistics, where one specifically doesn’t want to introduce “novel” methods without benchmarking them somehow. So there’s a valid reason to study the MBH network in the same sense; it has the added advantage of not being a particularly consistent data set and so it’s a good way to study weird statistical effects that are hard to study with sensible data.
Aside from that, as we’ve observed, the MBH98-99 data set continues in active use -used without modification in Rutherford et al 2005 and Mann et al 2007 without changing a comma, no concession whatever to the incorrect PC1 calculations or even the rain in Maine. So there hasn’t been a whole lot of “moving on” in the Mann camp anyway. And as we shall see, it’s baack, brassy as ever, in the most recent U.S. CCSP report, which I’ll discuss in a forthcoming post.
 The Texas Sharpshooter fallacy is a logical fallacy where a man shoots a barn thirty times then circles the bullet holes nearest each other after the fact calling that his target. It’s of particular concern in epidemiology.
The Texas Sharpshooter fallacy is a logical fallacy where a man shoots a barn thirty times then circles the bullet holes nearest each other after the fact calling that his target. It’s of particular concern in epidemiology.