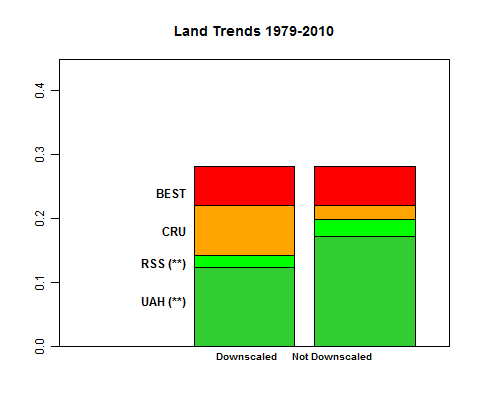
A few days ago, in a comment at CA, NASA blogger Gavin Schmidt stated that, over land, the ratio of lower troposphere trends to surface trends in the GISS ER model was 0.95 (+- 0.07) and thus there was no downscaling over land of tropospheric trends.
Schmidt linked to a November 2009 realclimate post, “Muddying the Peer Reviewed Literature”, which criticized Klotzbach et al 2009 for using an amplification factor of 1.2 over both land and ocean in their similar downscaling of satellite trends to surface for comparison to surface trends. (The realclimate post was published just before Climategate and not previously discussed here.)
Schmidt waxed eloquently against the Klotzbach et al article for being “heavily promoted”, containing “fundamental flaws” and wasting “a huge amount of everyone’s time” – a criticism that one feels would be more aptly directed at (say) Mann et al 2008, which “heavily promoted” their supposedly groundbreaking no-dendro reconstruction using upside-down and contaminated Tiljander sediment, with a “huge amount of everyone’s time” being wasted in dealing with the seemingly wilful obtuseness of both Schmidt and Mann in failing to retract or amend the original article and realclimate posts. But that’s another story.
Schmidt’s 2009 realclimate article also reported that the overall GISS ER amplification factor was 1.25 and, over ocean, was 1.4. describing the calculation as follows:
First I calculated the land-only, ocean-only and global mean temperatures and MSU-LT values for 5 ensemble members, then I looked at the trends in each of these timeseries and calculated the ratios. Interestingly, there was a significant difference between the three ratios. In the global mean, the ratio was 1.25 as expected and completely in line with the results from other models. Over the oceans where most tropical moist convection occurs, the amplification in the model is greater – about a factor of 1.4. However, over land, where there is not very much moist convection, which is not dominated by the tropics and where one expects surface trends to be greater than for the oceans, there was no amplification at all!
The land-only ‘amplification’ factor was actually close to 0.95 (+/-0.07, 95% uncertainty in an individual simulation arising from fitting a linear trend), implying that you should be expecting that land surface temperatures to rise (slightly) faster than the satellite values.
In response to Schmidt’s criticism, Klotzbach et al re-did their calculations in a correction, in which, instead of an overall amplification factor of 1.2 applied to both land and ocean, they used an amplification factor of 1.1 over land and 1.6 over ocean. (Re-reading Schmidt’s original post, one becomes aware of what Schmidt didn’t mention: he had drawn attention to and taken umbrage with Klotzbach’s too-high amplification factor over land, but not to the too-low amplification factor over ocean.)
Klotzbach et al (2010) stated that that they got similar results to the original article with these corrected amplification factors and did not retract the article as Schmidt had called for.
The discrepancy between the amplification factors used in Klotzbach et al 2010 and those reported by Schmidt at realclimate in November 2009 is an inconsistency that one feels that, purely as an empirical point, should be possible to resolve merely by trivial calculations on GISS ER runs.
Fresh Calculations
I’ve re-calculated tropospheric and surface trends over land, ocean and combined for the GISS models (including GISS ER) using Chad Herman’s excellent collation of A1B models (including GISS) that I placed online last week. Chad took care with land-ocean distribution, and, for the GISS runs, used the GISS land mask (see Chad’s documentation at climateaudit.info/data/chadh/src.rar.
The script for my calculations follow. These calculations closely replicate the amended values reported by Klotzbach et al 2010</a (note – see here for a discussion of these calculations, done by Ross McKitrick. I either wasn’t aware of this exchange or lost track of it during Climategate.)
For the period 1979-2008 (used by Klotzbach et al), I obtained an average GISS ER amplification factor over land of 1.10, exactly matching the Klotzbach et al 2010 results and outside the confidence intervals reported by Schmidt in November 2009 and re-iterated in his CA comment last week (0.95 +- 0.07). I experimented with other trend periods to try to match the Schmidt results and was unsuccessful. For the period 1979-2002 (which seems to have been used in Schmidt 2009), I got 1.057. For the A1B period 2010-2040, as an experiment, I got 1.107.
The methodology of my calculation matches Schmidt’s verbal description:
I looked at the trends in each of these timeseries and calculated the ratios
Nor does the discrepancy appear to arise from differences in gridcell allocation between land and ocean, since discrepancies in the same direction arise over ocean, where Schmidt reported an amplification factor of 1.4 (Klotzbach’s amended value was 1.6). I got 1.56 for the period 1979-2008 used by Klotzbach and 1.59 for the 1979-2002 period used by Schmidt, values that were close to those of KLotzbach et al 2010 and considerably higher than those reported by Schmidt.
On a combined based, Schmidt reported an amplification factor of 1.25, while I obtained a value of 1.36 for the 1979-2008 period (1979-2002: 1.345).
In summary, none of Schmidt’s results (land – 0.95; ocean – 1.4 and combined 1.25) were reproduced despite considerable care in the calculation. It would be nice to see the precise provenance of Schmidt’s results.
Update: Nov 7 11.30 am . Pielke Jr writes:
On your post today, you may want to look at this, in which Gavin explains his methods:
http://rogerpielkejr.blogspot.com/2009/08/exchange-with-gavin-schmidt-on.html
Our response to Gavin:
http://rogerpielkejr.blogspot.com/2009/11/response-to-gavin-schmidt-on-klotzbach.html
McKitrick on amplification ratios:
http://rogerpielkejr.blogspot.com/2009/11/mckitrick-on-amplification-ratios.html
Update Nov 8: Gavin Schmidt explained in a comment below that his result was calculated as follows:
Secondly, I calculated the amplification factors via linear regression of the annual anomalies of MSU-LT and SAT (1979-2005; GISS-ER only). You are calculating the ratio of two OLS trends.
There were two reasons why I calculated the ratio of the two OLS trends. It is what Gavin had said that he had done in the realclimate post. And it’s the right way to do the calculation. From Gavin’s comment, it seems that he regressed TAS~TLT or TLT~TAS. By experimenting, it seems evident that he regressed TAS~TLT as this yields “amplification factors” in the reported range. However, this is an incorrect approach to the problem.
First, extending the script below, here is evidence that Gavin got his 0.95 through TAS~TLT regression:
input=land$anom
temp= Info$model=="giss_er"; sum(temp)
year= seq(1850,2099.99,1/12)
indexy= (1:3000) [year>=1979 &year<2005]
input= input[indexy,temp,1:2]; dim(input)
fm=list() #TAS~TLT
for(i in 1:5) fm[[i]]= lm(TAS~TLT, data.frame(input[,i,]) )
round(sapply(fm,coef),3)[2,] # 1.059 0.977 0.920 0.932 0.951
round(mean(sapply(fm,coef)[2,]),3) #0.968
fmi=list() #TLT~TAS
for(i in 1:5) fmi[[i]]= lm(TLT~TAS, data.frame(input[,i,]) )
round(1/sapply(fmi,coef),3)[2,] # 1.369 1.313 1.249 1.166 1.295
round(1/mean(sapply(fmi,coef)[2,]),3) # 1.275
As discussed in comments, this is not the correct approach to the problem. The correct approach was the straightforward one said to have been used: the ratio of the trends. This can be seen in the diagram shown below where the blue (“pseudo-TLT”) series goes up at a higher trend (0.1 units/year) than the green (“pseudo-TAS”) series (0.05 units/year) – an “amplification factor” of 2, but has a lower variability (both have the same rnorm error, but the blue series has an amplitude of 0.25 of the green series).

If you take the trends of each series and divide, you get a value of around 2 (1.96 in the example that I did.) However, if you regress “TAS” against “TLT”, you get a coefficient of 0.598. If you regress “TLT” against “TAS”, you get a value of 0.91. Neither value is remotely close to the true (by construction) value of 2. Actually, it seems to me that the reciprocal of the coefficient from Schmidt’s regression of TAS~TLT would be less bad than the coefficient that he seems to have used. In this case, it would give a value of 1/.598 = 1.672, much closer to the true value than the estimate from Schmidt’s method. In the original case, the reciprocal of Schmidt’s value of 0.95 gives a value of 1.05, which is less than the actual ratio of trends, but again less bad.
But it’s easy enough to calculate the ratio of trends. I think that this small problem can now be said to be resolved.
Script
First download the collated runs. The script below collects previously collated data from by 3 satellite levels for 57 A1B runs of 24 models into three matrices (land, ocean, land-and-ocean) of dimension 3000 x 57 x 3.
get.data=function (zone="GLOBAL",firma="land",dset="sat") {
loc=paste("http://www.climateaudit.info/data/chadh/",zone,"/",dset,"/",firma,".tab",sep="")
download.file(loc,"temp",mode="wb")
load("temp")
Runs=list()
Runs$raw=runs
for(k in 1:3) runs[,,k]= apply(runs[,,k],2,anom)
Runs$anom=runs
return(Runs)
}
year= c(time( ts(1:3000,start=1850,freq=12)))
anom= function(x,start=1961,end=1991){
temp= year>=start& year <end
x- rep(unlist(tapply(x[temp], rep(1:12,30) , mean, na.rm = TRUE)), length(x)/12)
}
land=get.data(zone="GLOBAL",firma="land",dset="sat")
ocean=get.data(zone="GLOBAL",firma="ocean",dset="sat")
loti=get.data(zone="GLOBAL",firma="loti",dset="sat")
Next calculate trends for the various windowed periods.
trend=function(x) if(sum(!is.na(x))>10) lm(x~I((1:length(x))/120))$coef[2] else NA
get_trend=function(input, start=1979,end=2008.99) {# function to output trends from R-tables collected in previous step
N=dim(input)[[2]];K=dim(input)[[3]]
Out=array(NA,dim=c(N,K) )
h = function(x) anom(x, 1961, 1990)
for (k in 1:K) {
work= ts(input[,,k],1850, freq=12)
Out[,k]= round(apply( window( work, start,end),2,trend),3)
}
dimnames(Out)[[2]]= dimnames(input)[[3]]
dimnames(Out)[[1]]= dimnames(input)[[2]]
model= sapply (strsplit(dimnames(Out)[[1]],"_run"), function(A) A[[1]])
Outm = data.frame( round(apply(Out, 2, function(x) tapply(x, factor(model),mean,na.rm=T) ),3) )
Outm$ampl=round(Outm$TLT/Outm$TAS,3)
row.names(Outm)=paste("#", row.names(Outm) )
return(Outm[,c(1,2,4)])
}
##LAND
#Schmidt: The land-only ‘amplification’ factor was actually close to 0.95 (+/-0.07, 95% uncertainty in an individual simulation
temp= grep("giss", dimnames(land$raw)[[2]]);length(temp) #13
get_trend(land$anom[,temp,],start=1979,end=2007.99)
# TAS TLT ampl
# giss_aom 0.174 0.187 1.075
# giss_eh 0.234 0.264 1.128
# giss_eh2 0.248 0.267 1.077
# giss_er 0.260 0.287 1.104
get_trend(land$anom[,temp,],start=1979,end=2001.99)[4,]
#giss_er 0.228 0.241 1.057
get_trend(land$anom[,temp,],start=1979,end=2011.99)[4,]#to 2011
# giss_er 0.27 0.291 1.078
get_trend(land$anom[,temp,],start=2010,end=2039.99)[4,]
# giss_er 0.252 0.279 1.107
##OCEAN
#Schmidt: Over the oceans where most tropical moist convection occurs,
#the amplification in the model is greater – about a factor of 1.4.
get_trend(ocean$anom[,temp,],start=1979,end=2007.99)[4,]
## giss_er 0.151 0.236 1.563
get_trend(ocean$anom[,temp,],start=1979,end=2001.99)[4,]
## giss_er 0.115 0.183 1.591
get_trend(ocean$anom[,temp,],start=2010,end=2039.99)[4,]
## # giss_er 0.168 0.246 1.464
#BOTH
#Schmidt: In the global mean, the ratio was 1.25 as expected and completely in line #with the results from other models.
get_trend(loti$anom[,temp,],start=1979,end=2008.99)[4,]
# giss_er 0.185 0.252 1.362
get_trend(loti$anom[,temp,],start=1979,end=2001.99)[4,]
# giss_er 0.148 0.199 1.345