Here are some more notes and scripts in which I’ve made considerable progress on GISS Step 2. As noted on many occasions, the code is a demented mess – you’d never know that NASA actually has software policies (e.g. here or here . I guess that Hansen and associates regard themselves as being above the law. At this point, I haven’t even begum to approach analysis of whether the code accomplishes its underlying objective. There are innumerable decoding issues – John Goetz, an experienced programmer, compared it to descending into the hell described in a Stephen King novel. I compared it to the meaningless toy in the PPM children’s song – it goes zip when it moves, bop when it stops and whirr when it’s standing still. The endless machinations with binary files may have been necessary with Commodore 64s, but are totally pointless in 2008.
Because of the hapless programming, it takes a long time and considerable patience to figure out what happens when you press any particular button. The frustrating thing is that none of the operations are particularly complicated. Relevant scripts are or will be online here.
I’ve excerpted major chunks below, but you’re better off to cut and paste from an ASCII version as WordPress does odd things to quotation signs. I’ve placed tools online so anyone that’s interested can experiment with arbitrary stations. In a companion post, I’ll illustrate some methods of analyzing individual stations.
Tidying Dset1
One problem for organized programming is that the output of dset1 is a mess. There are 7364 stations, but some of these stations have more than one version so that there are 7716 different versions in dset1. The versioning is different than dset0, since these are not scribal variations but time variations. Programming is complicated by the fact that some (100) versions don’t have any data in them. I’m not sure why these versions are even created, but that’s merely one of the pointless land mines for users that Hansen has created. I haven’t figured out why different dset1 versions are created in some cases, while in others, there are long NA periods between data. A problem for another day.
For dset2 calculations, only versions with 20 years of data were considered. In the dset2 calculations, annual anomaly versions of “Hansen-rural” dset1 stations are used, with the same station often contributing to multiple urban adjustments. In order to do this coherently, I created a list in which I identified the dset1 versions (together with the station and relevant station information) with at least 20 years of data. From the 7716 versions, 100 versions were excluded as having no data whatever (!) and another 1473 versions for having less than 20 years of data, leaving 6143 versions. An information file station_versions.tab and a file consisting of 6143 time series of annual anomalies giss.anom.tab were created. I’ve uploaded the collation script as collation.giss.anom.txt, but interested users would probably be better off downloading my collations.
This was one of those exercises that doesn’t look like much in retrospect, but was done only after battering my head against the wall. The actual script doesn’t take all that long to run even on a home computer.
Wrapper Function
I’ve organized the following functions in a wrapper function emulate_dset2(id0), which will return the emulated dset2 series and intermediate diagnostics for a given station id. The steps in the wrapper function are described below.
Making a Rural Network for Comparison
The first step is collecting the Hansen-rural stations for comparison. For present purposes, we’re only discussing ROW stations, where Hansen-rural is triggered by a GHCN classification as R-rural, a classification readily seen to be extremely flawed (See past CA posts). But hey, why would NASA care? It’s been peer-reviewed. Hansen has a two-stage inspection in which he first searches for stations within 500 km and if he has “enough”, uses those, otherwise he proceeds to 1000 km. I’ve implemented the search using a function ruralstations (id0) , which uses a function circledist. I’ve used a slightly different strategy in which I’ve first created a short list of stations using a type of “Manhattan” metric set a little larger than 1000 km and then calculated great circle distances for these stations, taking the 500 km subset if there are enough. This type of vector processing is more efficient than Hansen’s endless obsolete do loops. This function takes a negligible amount of time to run for a given station.
circledist =function(loc, lat,long,R=6372.795) {
N=length(lat)
if(N==0) circledist=NA else {
pi180=pi/180;
x= abs(long -loc[2])
if (N>1) delta= apply( cbind(x %%360,(360-x)%%360),1,min) *pi180 else delta= min (x %%360,(360-x)%%360) *pi180
loc=loc*pi180; lat=lat*pi180; long=long*pi180
theta= 2* asin( sqrt( sin( (lat- loc[1])/2 )^2 + cos(lat)*cos(loc[1])* (sin(delta/2))^2 ))
circledist=R*theta
}
circledist
}
ruralstations=function(id0) {
if(is.numeric(id0)) i=id0 else i= (1:7364)[!is.na(match (names(giss.dset1),id0))]
temp_rur=(station_versions$urban==”R”)
station_versions$dist=NA
lat0=stations$lat[i];long0=stations$long[i]
temp1= (abs (station_versions$lat-lat0) <10) # & !is.na(station_versions$start_raw)
#initial screening only by latitude: must be within 10 deg latitude to be within 1000 km
test_angle= 10/sin(abs(lat0)*pi180)
x= abs(station_versions$long -long0)
delta= apply( cbind(x %%360,(360-x)%%360),1,min)
temp2=(delta<test_angle )
#second screen: within 1000 km by longitude
ruralstations=station_versions[temp1&temp2&temp_rur,c("station","version","name","long","lat","alt","dist","urban","lights")]
#matrix of stations meeting first two screen tests
ruralstations$dist=circledist(loc=c(lat0,long0),lat=ruralstations$lat,long=ruralstations$long)
#calculate circle distance for all stations in first screen
temp=(ruralstations$dist<=1000)&!is.na(ruralstations$dist)
if(sum(temp)==0) ruralstations= NA else {
ruralstations=ruralstations[temp,] #restrict to stations within 1000 km
temp=(ruralstations$dist=3) ruralstations=ruralstations[temp,]
ruralstations=ruralstations[order(ruralstations[,”dist”]),]#order by increasing distance
ruralstations$weights= 1- ruralstations$dist/1000}
ruralstations
}
Hansen’s actual selections can be decoded from the file PAPARS.GHCN.CL.1000.20.log. I wrote a function to extract information for individual stations from these logs as follows ( a function that I will add to.)
extract.log=function(id0){
index=grep(substr(id0,4,11),paparsghcn.log);
test=paparsghcn.log[index[1]:(max(index)+300)]
K=min(grep(“possible range”,test))
test1=test[1:K];
test2= paparslist[c(1,grep(substr(id0,4,11),paparslist))]
test2[2]=gsub(“-“,” “,test2[2])
writeLines(test2,”temp.dat”)
test2=read.table(“temp.dat”,colClasses=c(“character”,rep(“numeric”,13)),skip=1)
name0=c(scan(“temp.dat”,n=9,what=””),”M0_start”,”M0_end”,”M1_start”,”M1_end”,”flag”)
names(test2)=name0
extract.log=list(test1,test2)
extract.log
}
By calling log0=extract.log(id0), the first item log0[[1]] is the list of rural stations that Hansen selected.
I got exact matches for Wellington NZ and Batticaloa, both with small comparanda networks. In a larger test (Changsha), I extracted one more station than Hansen did, with Hansen apparently not picking up Zhijiang (20557745000) for reasons that are presently obscure. A project for another day.
Making the Reference Series
From the “rural” network, Hansen makes one reference series weighting each station in proportion to its distance from the target and folding in each station in order of decreasing length, adding/substracting an amount to the entering series to ensure that it has the same average as the prior entrants over the overlap period. I’ve done this in a function hansenref (rural) which uses the information from the rural network. This calculation relies on the prior tidying of the dset1 network. It returns the reference series, the rural anomaly network and the count of non-NA values by year, the latter two useful in diagnostics.
hansenref=function(rural) {
K=nrow(rural)
#collate rural anom
anom.rural=NULL
for (k in 1:K) anom.rural=ts.union(anom.rural,giss.anom[[ paste(rural$version[k]) ]])
dimnames(anom.rural)[[2]]=rural$version
#cross check to binary should be OK
N=nrow(anom.rural)
W=t(array(rep(rural$weights,N),dim=c(length(rural$weights),N) ) )
W[is.na(anom.rural)]=NA
#matrix of weights: at least 3 stations and station available
long0=apply(!is.na(anom.rural),2,sum)
#calculates length of the candidate rural series
order1=order(long0,decreasing=TRUE);index=NULL
#long0[order1] # orders by decreasing length
delta=NULL
fixed=NULL; available= 1:K;
#start with the longest series
if (max(long0)<20) reference=NA else {
j0=order1[1];
reference=anom.rural[,j0] #picks longest series to insert
reference.seq=reference
weights1=W[,j0]
fixed=j0
#sequentially adds in the rural series
for (k in 2:K) {
j0=order1[k] #chooses the series to be added
Y=cbind(anom.rural[,j0],reference,W[,j0],weights1,reference);
temp=!is.na(Y[,1])&!is.na(Y[,2])
#if(sum(temp)>=20) {
bias= mean(Y[temp,1])-mean(Y[temp,2])
#in this case, there is a long separation: what happens then
Y[,1]=Y[,1]-bias #these have same centers
g=function(x) weighted.mean(x[1:2],x[3:4],na.rm=T)
Y[,5]=apply(Y[,1:4],1,g)
fixed=c(fixed,j0)
reference=Y[,5]
delta=c(delta,bias)
reference.seq=cbind(reference.seq,reference)
weights1=apply(Y[,3:4],1,sum,na.rm=T)
}
}
count=ts(apply(!is.na(anom.rural),1,sum),start=tsp(anom.rural)[1])
hansenref=list(reference,count,anom.rural,W);
names(hansenref)=c(“reference”,”count”,”anom”,”weights”)
hansenref
}
Annual Adjustments
The next step is to calculate an annual adjustment series. For Wellington NZ, the adjustment exactly matches the actual dset2 minus dset1 difference. For Batticaloa, it is mostly exact, but is off by 0.1 deg in occasional step years. For Changsha, it doesn’t presently match. So I’m only partway there, but feel that I’ve got the main components.
The adjustment process is seriously weird. I haven’t gone back to the text yet to see how much of this is described in the text, but my guess is that some key steps will not have been described or will have been incompletely described.
My present surmise is that Hansen first tries the “two legged fit” on the continuous subset where there are at least 3 stations. The resulting slopes are then tested against various “flags” (which reject among other things too great a slope in one leg or too great a difference between legs). If the two-legged fit fails any of these tests, it goes back to one legged fit (Wellington is a case where it reverts back to a one-legged fit.) In fact, there are a LOT of one-legged fits in the entire inventory. Call this first range of years M0 (1951-1984 for Wellington).
Hansen also likes to zero things to the present (resulting in constant re-writing of history). It appears that the adjustment is zeroed on the last year of the M0 segment, by subtracting the last adjustment value in the range.
Hansen now arbitrarily expands this range by 50%, allocating the range extension first to any portion of the urban record more recent than the end of the M0 range (1989 for Wellington, with the balance extending the early portion, thus to 1939 in Wellington.) The M1 range is 1939-1989. The adjustment in the extended range is bewildering even for Hansen. He just uses the first and last M0 values in the respective range extensions, regardless of the actual reference series. When you plot up the Hansen adjustment against the difference between the reference series and the urban series (Which gives rise to the adjustment), the inconsistencies can be huge, to say the least.
Bulding the Monthly dset2 Series
The monthly dset2 series is in monthly average (not anomaly). To rebuild the “adjusted” dset2 version, Hansen spreads the annual adjustment into months, starting each year in the prior December. The monthly norms from the original anomaly calculation are recalled and used to re-scale the series. This step can be done pretty easily.
Wrapper Function Again
I’ve collected all the various intermediates as output from the wrapper function emulate_dset2. So for example, the command:
W=emulate_dset2(id0)
yields the following components:
W$annual: a time series of annual series, including the emulated adjustment and dset2 emulations
W$monthly: same for monthly series
W$adj: results from the two-legged adjustment including both two-legged W$adj$model and one-legged W$adj$fm0
W$rural: info on the rural comparanda
W$info: info on the urban station
W$reference: results from the reference calculation – W$reference$reference – the reference comparandum; W$reference$anom, the rural anomaly network;
W$M0, W$M1 – the 3-station and extended dates.
These can be used for diagnostics. I don’t think that there is any material extra time in collecting things, but, if necessary, once all the corners have been inspected, a pared down function could be used to return the dset2 emulation. At some point, this sort of trail can be used to keep track of exactly what weights are being assigned to the various stations.
emulate_dset2=function(id0) {
#id0=”50793436001″
rural=ruralstations(id0)
#collate urban target
if (is.numeric(id0) &(id0<8000)) i=id0 else i=(1:7364)[(names(giss.dset1)==id0)]
dset1.monthly=ts( c(t(giss.dset1[[i]][[1]][,2:13])) ,start=c(giss.dset1[[i]][[1]][1,1],1),freq=12)
dset1.annual= ts(giss.dset1[[i]][[1]][,18], start=giss.dset1[[i]][[1]][1,1])
dset1.monthly.anom=anom(dset1.monthly,method=”hansen”)
dset1.norm=dset1.monthly.anom[[2]];dset1.monthly.anom=dset1.monthly.anom[[1]]
dset1.annual.anom=hansenq(dset1.monthly.anom,method=”ts”)[,5]
dset1.count= ts( apply(!is.na(giss.dset1[[i]][[1]][,14:17] ),1,sum,na.rm=TRUE),start=giss.dset1[[i]][[1]][1,1])
dset2.monthly=ts( c(t(giss.dset2[[i]][[1]][,2:13])) ,start=c(giss.dset2[[i]][[1]][1,1],1),freq=12)
dset2.annual= ts(giss.dset2[[i]][[1]][,18], start=giss.dset2[[i]][[1]][1,1])
dset1.info=stations[i,]
#collate rural station comparanda
reference0=hansenref(rural)
count=reference0$count
reference=reference0$reference
#reference
Y=ts.union(dset1.annual,dset1.annual.anom,dset2.annual,dset2.annual,reference,reference,reference,reference,dset1.count,count,reference)
Y=cbind(Y,c(time(Y)))
dimnames(Y)[[2]]=c(“dset1.book”,”dset1.anom”,”dset2.book”,”delta”,”reference”,”adjusted”,”adjustment”,”emulation”,”urban.count”,”dset1.count”,”pre_adj”,”year”)
Y[,c(“delta”,”adjustment”,”adjusted”,”emulation”,”pre_adj”)]=NA
Y[,”delta”]=Y[,”dset2.book”]-Y[,”dset1.book”]
temp0=(Y[,”dset1.count”]>=3)&!is.na(Y[,”dset1.count”])&!is.na(Y[,”dset1.anom”])
M0=range(time(Y)[temp0]) #range of available
#temp0=(time(Y)>=M0[1])&(time(Y)=3 in range with count>=3
N3ext=floor(N3*1.5)
#temp4=(Y[,”dset1.count”]>0)&!is.na(Y[,”dset1.count”])&(count>0)&!is.na(count)
temp4=(Y[,”dset1.count”]>0)&!is.na(Y[,”dset1.count”])&(Y[,”urban.count”]>0)&!is.na(Y[,”urban.count”])
M1=c(NA,max(c(time(Y))[temp4]) ) #1988
M1[1]=M1[2]-N3ext+1;M1
y=Y[,”reference”]-Y[,”dset1.anom”]
adj=twoleg(ts(y[temp0],start=M0[1]))
if ((adj$flag==0)|(adj$flag==100)) x=fitted(adj$model) else x= fitted(adj$fm0)
#round(x,1)
Y[temp0,”pre_adj”]=round(x,1)
x=x-x[length(x)]
Y[temp0,”adjustment”]=round(x,1)
temp1A=(time(Y)>=M1[1])&!is.na(Y[,”dset1.anom”])&(time(Y)<m0 [1])
temp1B=(time(Y)M0[2])
Y[temp1A,”adjustment”]=round(x[1],1)
Y[temp1B,”adjustment”]=round(x[length(x)],1)
Y[,”adjusted”]=round(Y[,”dset1.anom”]+Y[,”adjustment”],2)
##now rebuild monthly series
Z=ts.union(dset1.monthly,dset1.monthly.anom,dset2.monthly,dset2.monthly,dset2.monthly,dset2.monthly,dset2.monthly)
dimnames(Z)[[2]]=c(“dset1.book”,”dset1.anom”,”dset2.book”,”adjustment”,”adjusted”,”emulation”,”delta”)
Z[,4:7]=NA
temp2=(time(Y)>=tsp(Z)[1])&(time(Y)< =tsp(Z)[2])
x= c(t(array(rep(Y[temp2,"adjustment"],12),dim=c(nrow(Y[temp2,]),12)) ))
Z[,"adjustment"]=c(x[2:length(x)],NA)
Z[,"adjusted"]=round(Z[,"adjustment"]+Z[,"dset1.anom"],2)
X= t(array(Z[,"adjusted"],dim=c(12,nrow(Z)/12) ))
Z[,"emulation"]= c(t(scale(X,center= -dset1.norm,scale=FALSE) ))
Z[,"delta"]=round(Z[,"emulation"]-Z[,"dset2.book"],2)
#hansenq(Z[,"emulation"],method="ts")
emulate_dset2=list(Y,Z,reference0,rural,M0,M1,adj,dset1.info)
names(emulate_dset2)=c("annual","monthly","reference","rural","M0","M1","adj","info")
emulate_dset2
}
Benchmarking
Wellington NZ
Here are some diagnostic plots illustrating the use of this function for diagnostics. First we execute the wrapper function using the station id and the extraction function from unzipped Hansen logs.
id0=”50793436001″
W=emulate_dset2(id0)
log0=extract.log(id0)
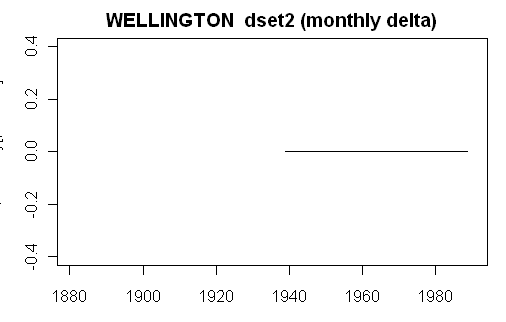
First here is a simple plot comparing the actual delta (dset2 minus dset1) to the calculated adjustment (here for monthly results), a plot obtained very simply as follows:
plot.ts(W$monthly[,”delta”]-W$monthly[,”adjustment”],ylim=c(-.4,.4),main=paste(W$info$name,” dset2 (monthly delta)”))
This yields the following graphic, which, in this case, shows an exact match. So something has been rescued from the living hell of Hansen’s code, though other stations don’t work yet.
Here is a more detailed diagnostic plot, showing a variety or relevant adjustment information. First, I show here (black solid) the actual (rural reference minus the dset1 target) that gives rise to the ultimate adjustment (black dashed). Second, in green, I show the two-legged and one-legged fits over the M0 period (here these come from W$adj$model$fitted.values and W$adj$fm0$fitted.values), both being readily accessible from the list of outputs. In this case, these can be matched exactly to values extracted from Hansen’s PAPARS.list file, though this requires a little interpretation and head-scratching. Interpretations are plotted here in cyan and can be seen to match my fits in this case. All the values in Hansen’s log were divided by 10 to yield deg C, which is plotted here and is the unit of interest. Second, in this case, Hansen shows two positive slopes, but the results here require that the 2nd slope be negative. I haven’t checked how this affects flag tests. In red, I’ve shown first the impact of rounding to even 0.1 deg C and then the series displaced so that the last M) value of the adjustment is 0, together with extensions to the M1 range. This yields the exact match to the observed dset2 minus dset1 adjustment.
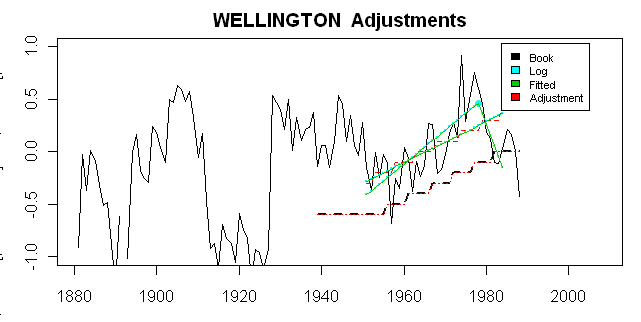
Here’s the code to generate the graphic shown here:
year=c(time(W$annual))
layout(1);par(mar=c(3,3,2,1))
plot(year,W$annual[,”reference”]-W$annual[,”dset1.anom”],type=”l”,ylim=c(-1,1))
lines(year,W$annual[,”delta”],lty=2,lwd=2)
lines(year,W$annual[,”adjustment”],lty=3,col=2)
lines(year,W$annual[,”pre_adj”],lty=2,col=2)
a=log0[[2]];xmid=a$knee
points(xmid,a$Yknee/10,pch=19,col=5)
x=W$M0[1]:W$M0[2];
temp=(x =log0[[2]]$knee);sum(temp)
points( x[temp], 0.1*(a$Yknee – a$sl2*(x[temp]-xmid) ) ,col=5,pch=19,cex=.1)
#note that this is minus sl2 and plus sl1
points( x, 0.1*(a$Ymid + a$slope*(x-xmid) ) ,col=5,pch=19,cex=.1)
lines(W$M0[1]:W$M0[2],W$adj$model$fitted.values,col=3,lty=1)
lines(W$M0[1]:W$M0[2],W$adj$fm0$fitted.values,col=3,lty=1)
title(paste(W$info$name,” Adjustments”))
legend(locator(1),fill=c(1,5,3,2),legend=c(“Book”,”Log”,”Fitted”,”Adjustment”),cex=.7,box.lwd=0)







