One of Hansen’s pit bulls, Tamino, has re-visited Mannian principal components. Tamino is a bright person, whose remarks are all too often marred by the pit bull persona that he has unfortunately chosen to adopt. His choice of topic is a curious one, as he ends up re-opening a few old scabs, none of which seem likely to me to improve things for the Team, but some of which are loose ends, and so I’m happy to re-visit them and perhaps resolve some of them. Tamino’s post and associated comments are marred by a number of untrue assertions and allegations about our work, a practice that is unfortunately all too common within the adversarial climate science community. When Tamino criticizes our work, he never quotes from it directly – a practice that seems to have originated at realclimate and adopted by other climate scientists. Thus his post ends up being replete with inaccuracies whenever it comes to our work.
Tamino’s main effort in this post is an attempt to claim that Mannian non-centered principal components methodology is a legitimate methodological choice. This would seem to be an uphill fight given the positions taken by the NAS Panel and the Wegman Panel – see also this account of a 2006 American Statistical Association session. However, Tamino makes a try, claiming that Mannian methodology is within an accepted literature, that it has desirable properties for climate reconstructions and that there were good reasons for its selection by MBH. I do not believe that he established any of these claims; I’ll do a post on this topic.
In the course of this exposition, Tamino discusses the vexed issue of PC retention for tree ring networks, claiming that MBH employed “objective criteria” for retaining PCs. I am unaware of any methodology which can successfully replicate the actual pattern of retained PCs in MBH98, a point that I made in an early CA post here. This inconsistency has annoyed me for some time and I’m glad that Tamino has revived the issue as perhaps he can finally explain how one actually derives MBH retention for any case other than the AD1400 NOAMER network. I’ll do a detailed post on this as well.
Whenever there is any discussion of principal components or some such multivariate methodology, readers should keep one thought firmly in their minds: at the end of the day – after the principal components, after the regression, after the re-scaling, after the expansion to gridcells and calculation of NH temperature – the entire procedure simply results in the assignment of weights to each proxy. This is a point that I chose to highlight and spend some time on in my Georgia Tech presentation. The results of any particular procedural option can be illustrated with the sort of map shown here – in which the weight of each site is indicated by the area of the dot on a world map. Variant MBH results largely depend on the weight assigned to Graybill bristlecone chronologies – which themselves have problems (e.g. Ababneh.)
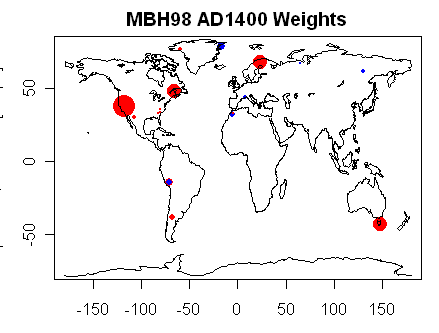
Figure 1. Each dot shows weights of AD1400 MBH98 proxies with area proportional to weight. Major weights are assigned to the NOAMER PC1 (bristlecones), Gaspe, Tornetrask and Tasmania. Issues have arisen in updating each of the first three sites.
Readers also need to keep in mind that two quite distinct principal component operations are carried out in MBH98 – one on gridded temperature data from CRU; and one on tree ring networks from ITRDB and elsewhere. The characteristics of the networks are very different. The gridded temperature networks result in a matrix of data with some effort at geographic organization, while there is no such attempt in the tree ring networks. The tree ring networks are more like the GHCN station networks than like a gridded network. For comparison, imagine a PC calculation on station data in the GHCN network going prior to 1930 with no attempt at geographic organization or balance. Followers of this discussion realize that long station data is overwhelmingly dominated by U.S. (USHCN) station information. Actually, the tree ring networks are even more disparate than GHCN station networks. Many of the tree ring sites are limited by precipitation. Thus, PC on the tree ring networks is more like doing a PC analysis on a pseudo-GHCN network consisting of mostly of precipitation measurements with some blends of temperature and precipitation, with a predominance of stations from the southwest U.S. There are obviously many issues in trying to transpose Preisendorfer methodology developed for very specific circumstances to this sort of information.
Before getting to either of the above larger topics, I wish to lead in with a discussion of the PC calculations in the gridded temperature network – something that hasn’t been on our radar screens very much, but which may shed some light on the thorny tree ring calculations. Here there is some new information since early 2005 – the source code provided to the House Energy and Commerce Committee shows the “Rule N” calculation for gridded temperature networks (though not for tree ring networks) and, in the absence of other information, can help illuminate obscure Mannian calculations.
In the course of this review, I also reconsidered Preisendorfer 1988, Mann’s cited authority for PCA. Preisendorfer (1988), entitled “Principal Component Analysis in Meteorology and Oceanography”, is an interesting and impressive opus, with many interesting by-ways and asides. Preisendorfer is clearly an experienced mathematician and his results are framed in mathematical terms, rather than ad hoc recipes. Many of his comments remain relevant to the present debate, . Continue reading