Climate Audit

by Hu McCulloch

A recent discussion of the 2007 Tellus paper by Bo Li, Douglas Nychka and Caspar Ammann, “The ‘hockey stick’ and the 1990s: a statistical perspective on reconstructing hemispheric temperatures,” at OSU by Emily Kang and Tao Shi has prompted me to revive the discussion of it with some new observations. A PDF of the paper is online at Li’s NCAR site.

The 8/29/07 CA thread MBH Proxies in Bo Li et al has already discussed certain data issues in depth, but the 11/18/07 general discussion Li et al 2007 never really got off the ground. (See also a few comments by Jean S and others in an unrelated CA thread.)

The lead and corresponding author, Bo Li, is an energetic young statistician (PhD 2006) at NCAR. Presumably her role was to bring some new statistical techniques to bear on the problem, while the two senior authors provided most of the climatology know-how. I’ll start with my positive comments, and then offer some criticisms.

My first upside comment is that the paper recalibrates the 14 MBH99 1000 AD proxies using the full instrumental period of 1850-1980, rather than just 1902-1980 as in MBH. Cross-validation with subperiods is a fine check on the results (see below), but in the end if you really believe the model, you should use all the data you can find to estimate it.

Secondly, I was happy to see that the authors simply calibrated the MBH proxies directly to NH temperature rather than to intermediate temperature PC’s as in MBH. Perhaps someone can correct me if I’m wrong, but I don’t see the point of the intermediate temperature PC’s if all you are ultimately interested in is NH (or global) temperature.

Third, although the cumbersome Monte Carlo simulation at first puzzled me, because confidence limits for the individual temperature reconstructions are calculable in closed form, it eventually became clear that this was done because the ultimate goal of the paper is to investigate the characteristically MBH question of whether current temperatures are higher than <i>any</i> previous temperature over the past 1000 years. A confidence interval for each year (or decade or whatever) does not answer this, because it merely places a probability on whether that particular year’s temperature was higher or lower than any given level. There is no closed form way to test the much more complex hypothesis that current temperatures are higher than <i> every </i/> past temperature. Monte Carlo simulations of past temperatures based on perturbations of the estimated coefficients potentially enable one to place probabilities on such statements. (I would call these “simulations” rather than “ensembles”, but perhaps that’s just a matter of taste.)

And fourth, the authors explicitly check for serial correlation in the residuals of their regression, find that it is present as AR(2), and incorporate it appropriately into the model. MBH seem to have overlooked this potentially important problem entirely.

Unfortunately, I see a number of problems with the paper as well.

My first criticism is that the authors start with an equation (their (1)) that is supposed to relate NH temperature to a linear combination of the MBH proxies, but then provide no indication whatsoever of the significance of the coefficients.

The whole difference between statistics and astrology is supposed to be that statisticians make statements of statistical significance to determine how likely or unlikely it is that an observed outcome could have happened chance, while astrologers are satisfied with merely anecdotal confirmation of their hypotheses. Perhaps climate scientists like MBH can’t be expected to know about statistical significance, but the omission is doubly glaring in the present paper, since Nychka is a statistician as well as Li.

The MBH proxies are perhaps sufficiently multicollinear that none of the individual t-statistics is significant. However, it is elementary to test the joint hypothesis that all the coefficients (apart from the intercept — see below) are zero with an F statistic. This particular test is known, in fact, as the Regression F Statistic. The serial correlation slightly complicates its calculation, but this is elementary once the serial correlation has been estimated. Or, since the whole system is being estimated by ML, an asymptotically valid Likelihood Ratio statistic can be used in its place, with what should be similar results. (My own preference would be to take the estimated AR coefficients as true, and compute the exact GLS F statistic instead.)

Since for all we know all the slope coefficients in (1) are 0, the paper’s reconstruction may just be telling us that given these proxies, a constant at the average of the calibration period (about -.15 dC relative to 1961-90 = 0) is just as good a guess as anything. Indeed, it doesn’t differ much from a flat line at -.15 dC plus noise, so perhaps this is what is going on. This is not to say that there might not be valid temperature proxies out there, but this paper does nothing to establish that the 14 MBH99 proxies are among them. (Nor did MBH, for that matter.)

My second criticism deals with the form of their (1) itself. As UC has already pointed out, this equation inappropriately puts the independent variable (temperature) on the left hand side, and the dependent variables (the tree ring and other proxies) on the right hand side. Perhaps tree ring widths and other proxies respond to temperature, but surely global (or even NH) temperature does not respond to tree ring widths or ice core isotope ratios.

Instead, the proxies should be individually regressed on temperature during the calibration period, and then if (and only if) the coefficients are jointly significantly different from zeros, reconstructed temperatures backed out of the proxy values using these coefficients. This is the “Classical Calibration Estimation” (CCE) discussed by UC in the 11/25/07 thread “UC on CCE”. The method is described in PJ Brown’s paper in the Proceedings of the Royal Statistical Society B;, 1982, (SM – now online here)and is also summarized on UC’s blog. See my post #78 on the “UC on CCE” thread for a proposed alternative to Brown’s method of computing confidence intervals for temperature in the multivariate case.

In this CCE approach, the joint hypothesis that all the slope coefficients are 0 is no longer the standard Regression F statistic. Nevertheless, it can still be tested with an F statistic constructed using the estimated covariance matrix of the residuals of the individual proxy calibration regressions. Brown shows, using a complicated argument involving Wishart distributions, that this test is exactly F in the case where all the variances and covariances are estimated without restriction.

To MBH’s credit, they at least employed a form of the CCE calibration approach, rather than LNA’s direct regression of temperature on proxies. There are, nevertheless, serious problems with their use (or non-use) of the covariance matrix of the residuals. See, eg, “Squared Weights in MBH98”> and “An Example of MBH ‘Robustness'”.>

One pleasant dividend that I would expect from using CCE instead of direct regression (UC’s “ICE” or Inverse Correlation Estimation) is that there is likely to be far less serial correlation in the errors.

My third criticism is that that even though 9 of the 14 proxies are treerings, and even though the authors acknowledge (p. 597) that “the increase of CO2 may accelerate the growth of trees”, they make no attempt to control for atmospheric CO2. Data from Law Dome is readily available from CDIAC from 1010 to 1975, and this can easily be spliced into the annual data from Mauna Loa from 1958 to the present. This could simply be added to the authors’ equation (1) as an additional “explanatory” variable for temperature, or better yet, added to each CCE regression of a treering proxy on temperature. Since, as MBH99 themseleves point out, the fertilization effect is likely to be nonlinear, log(CO2), or even a quadratic in log(CO2) might be appropriate.

Of course, any apparent significance to the treering proxies that is present will most likely immediately disappear once CO2 is included, but in that case so much for treerings as temperature proxies…

A fourth big problem is the data itself. The whole point of this paper is just to try out a new statistical technique on what supposedly is a universally acclaimed data set, so LNA understandably take it as given. Nevertheless, their conclusions are only as good as their data.

The authors do acknowledge that “many specific criticisms on MBH98” have been raised, but they do not provide a single reference to the papers that raised these objections. McIntyre and McKitrick 2003, MM05GRL and MM05EE come to mind. Instead, they cite no less than 6 papers that supposedly have examined these unspecified objections, and found that “only minor corrections were found to be necessary” to address the phantom-like concerns. LNA have no obligation to cite McIntyre and McKitrick, but is rather tacky of them not to if they cite the replies.

Many specific data problems have already been discussed on CA on the thread MBH Proxies in Bo Li et al and elsewhere on CA. See, in particular, the numerous threads on Bristlecone Pines. I might add that it is odd that MBH include no less than 4 proxies (out of 14) from the South American site Quelccaya in what is supposedly a study of NH temperature.

A fifth problem is with the author’s variance “inflation factor”. They commendably investigate k-fold cross-validation of the observations with k = 10 in order to see if the prediction errors for the withheld samples are larger than they should be. This makes a lot more sense to me than the “CE” and “RE” “validation statistics” favored by MBH and others. However, they appear to believe that the prediction errors should be of the same size as the regression errors. They find that they are in fact about 1.30 times as large, and hence inflate the variance of their Monte Carlo simulations by the same factor.

In fact, elementary regression analysis tells us that if an ols regression

has variance , the prediction errors for an out-of-sample value y* using a row vector of regressors x* should be , not itself.

Since the quadratic form in x* is necessarily positive, the factor is necessarily greater than unity, not unity itself. Exactly how much bigger it is depends on the nature and number of the regressors and the sample size. Using 10,000 Monte Carlo replications, with estimation sample size 117 and 14 regressors plus a constant, I find that if the X’s are iid N(0,1), the factor is on average 1.15, substantially greater than unity. If the X’s are AR(1) with coefficient 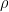= .8, and x* is the next element of this process, the factor rises to 1.19. With 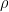= .9, it is 2.18 1.22 (corr. 11/17/12), and if the X’s are a random walk ( 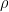= 1), it becomes 1.28, essentially the 1.30 found by LNA. So in fact their “inflation factor” may simply be what is expected when the model is perfectly valid. (These simulations take only about 10 seconds each on a PC in GAUSS.)

If the variance of the cross-validation prediction errors prediction errors were significantly greater than they should be according to the above formula, that in itself would invalidate the model, instead of calling for an ad hoc inflation of the variance by the discrepancy. The problem could be a data error (eg 275 punched in as 725), non-Gaussian residuals, non-linearity, or a host of other possibilities. In fact, the authors make no attempt to perform such a test. I don’t know whether it has an exact F distribution, but with two statisticians on board it shouldn’t have been hard to figure it out.

Although LNA make no use of the above prediction error variance formula in their reconstruction period, it is in fact implicit in their Monte Carlo simulations, since in each simulation they generate random data using the estimated parameters, and then re-estimate the parameters using the synthetic data and use these perturbed to construct one simulated reconstruction. They therefore did not need to incorporate their inflation factor into the simulations. They should instead have just used it to test the validity of their model.

One last small, but important point, is that their (1) does not include a constant term, but definitely needs one. Even if they de-meaned all their variables before running it so that the estimated constant will be identically 0, this still is a very uncertain “0”, with the same standard error as if the the dependent variable had not been demeaned, and will be an important part of the simulation error.

Anyway, a very interesting and stimulating article. I wish Dr. Li great success in her career!